ガンマ補正とは
例えば蝋燭の数を倍に増やすと明るさ(輝度)を表す数値も倍になる。そういった物理的な輝度と素直に比例する関係をリニアと呼びます。1
幾つかの理由で、このリニアな輝度値をそのまま記録したり転送に使うのは非効率なので、非リニアに変換する事が多く、ガンマ補正はその変換のひとつです。
 |
 
|
   
|
       
|
|
|---|---|---|---|---|
| 本数 | 1 | 2 | 4 | 8 |
| リニア (x10) | 10 | 20 | 40 | 80 |
| 非リニア(log_2) | 0 | 1 | 2 | 3 |
映像信号や画像ファイル等の RGB値は大抵の場合、この輝度リニアに対してガンマ補正か、それに似た変換がかかっています。
ガンマ補正の変換処理は以下の式で表されます。
y = x ^ γ (x, y は 0〜1 に正規化)
| γ=0.45 | γ=1.0 | γ=2.2 |
|---|---|---|
 |
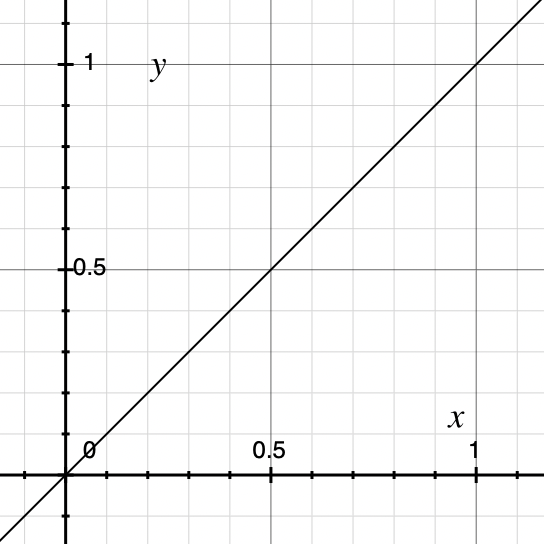 |
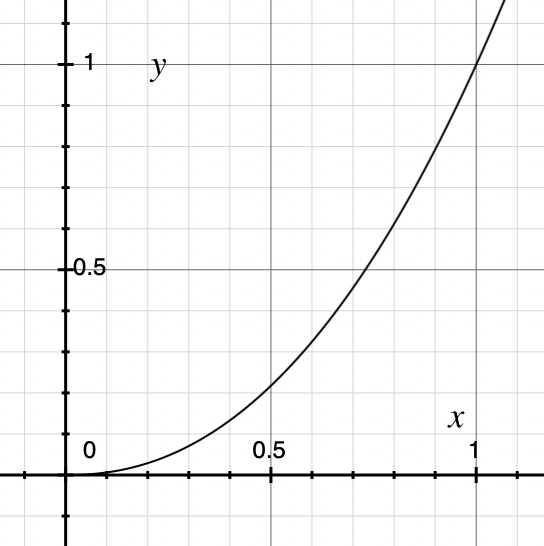 |
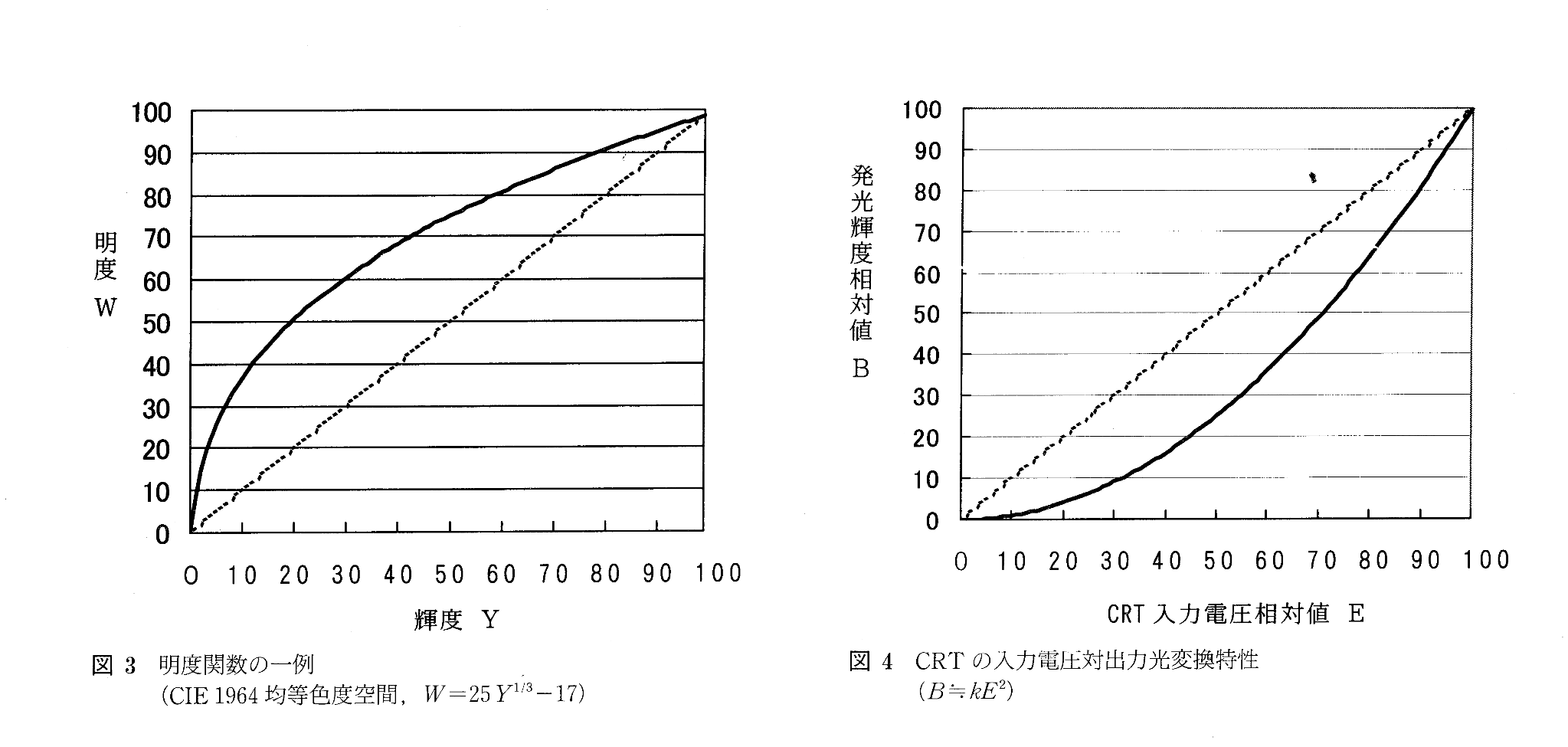
陰極管特性
昔のブラウン管テレビが陰極管の物理特性により入力信号の電圧に対して出力する輝度が比例しなかったので、信号側で補正する事にしたそうです。
- 参考) 1680万色の画像とは?
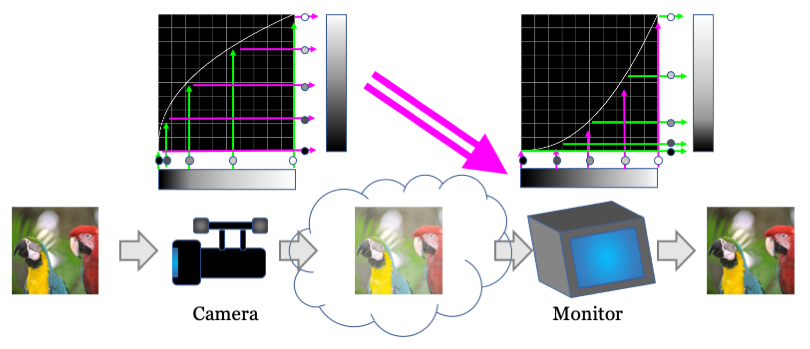
上の図でいうと、放送局側で画像信号を左のグラフのように逆ガンマ変換して電波送信し、受信した御家庭のテレビが右グラフのガンマ特性でリニアの輝度表示に戻す。そういう約束事です。
視覚心理特性
また、ガンマ補正は人間の視覚特性にも都合が良いです。
人間の感覚は刺激の物理強度にリニアではなく、その対数にフィットします。 Weber–Fechner(ヴェーバー‐フェヒナー)の法則として知られます。
| ガンマについて |
|---|
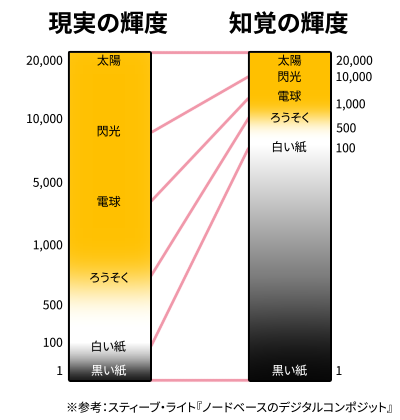 |
| http://compojigoku.blog.fc2.com/blog-entry-23.html |
これにより人の目は低輝度の変化に敏感、高輝度には鈍感です。ロウソクの数が倍々に増えていっても、人の眼には大体等間隔で明るく見えます。
そのため、リニア輝度でRGB値を表現するとデジタル値の処理につきまとう量子化誤差2が低輝度ほど目立ちます。ガンマ補正するとその傾向が薄れます。そういった視覚的なスケールに近付く利点があります。
ガンマカーブ
Y = Math.pow(X, gamma) // pow はべき乗の関数
(注) 輝度値が0〜255の場合は0〜1に正規化してガンマ補正します。
つまり Y = Math.pow(X/255, gamma)*255 です。
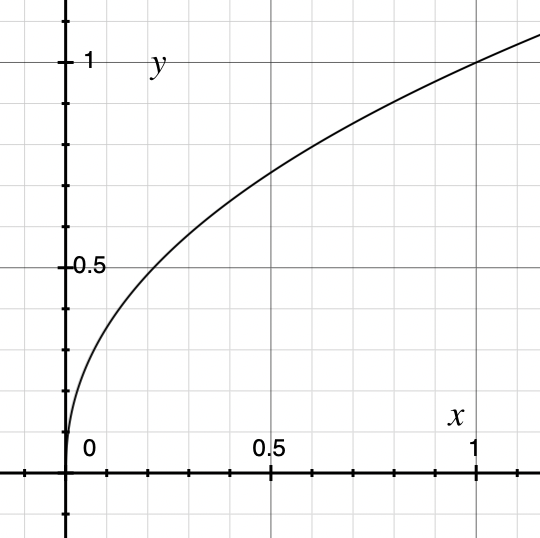
この式をグラフに描くと以下のようになります。
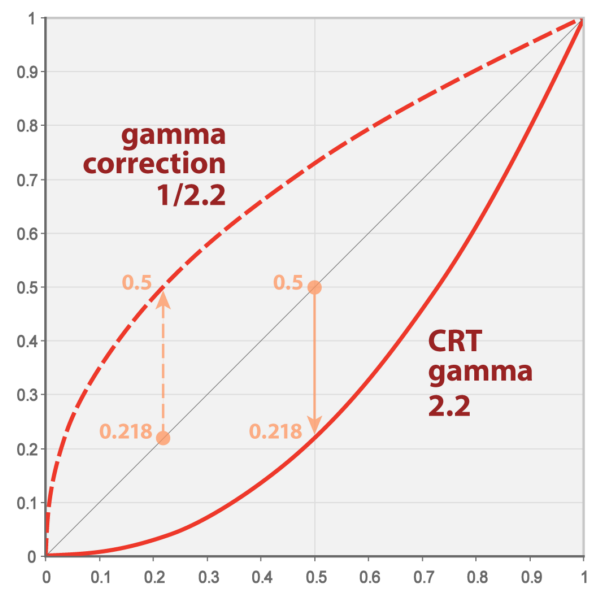 |
|---|
| (c) https://ja.wikipedia.org/wiki/ガンマ値 |
gamma:(1/2.2=0.4545...) で左上の点線カーブ、gamma:2.2 で 右下の実線カーブを描きます。0〜1 に対するべき乗なので、gamma値 が大きいほどカーブが引き下げられる事に注意して下さい。
昔のモニタの特性が下の実線カーブに近かったので、そのガンマ補正がかかるのを想定して、実際の輝度スケールに対し上の点線の補正をかける規格が RGB に適用されています。
メリット
冒頭で少し触れましたが、各家庭のテレビに入力電圧と輝度がリニアになるよう頑張る装置を載せるより、放送局側でガンマ補正した方が業界全体としてのコストが圧倒的に安いのがまず一点。
人の眼の視覚特性は低輝度の変化に敏感で高輝度で鈍感な性質があり、ガンマ補正はその点でも都合が良いです。
例えば階調が100分割だとしてガンマ補正された値は、上記グラフだと輝度50以下で 0〜73、50以上に 75〜100 の値が割り当たります。つまり低輝度の方が細かく表現できます。
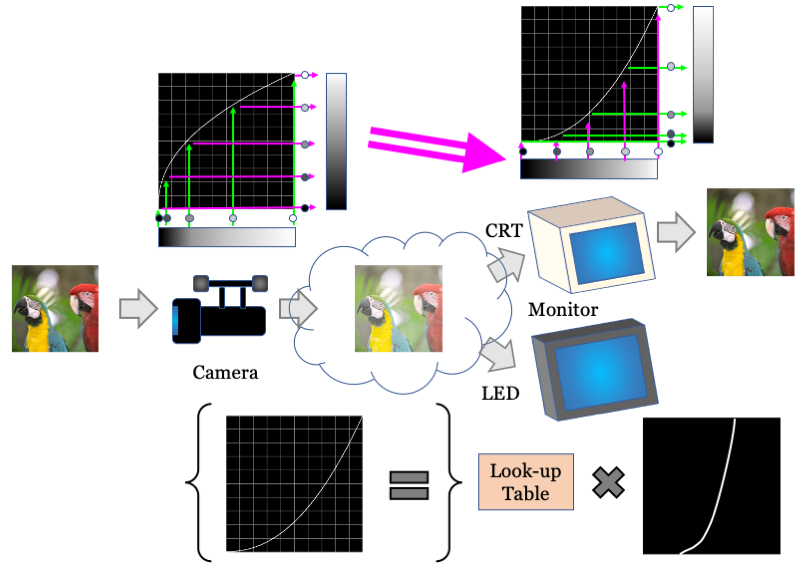
ブラウン管と異なり液晶ディスプレイの輝度出力にガンマ特性は存在しませんが、大抵は互換性の都合で sRGBガンマで信号をやりとりする為、LED特性に合わせて信号を Look-up Table 等で加工し、ブラウン管と同等の変換になるよう調整します。よって最終的な表示ではブラウン管同様に物理リニア輝度です。
実のところ、ブラウン管のガンマ特性も正確に 2.2 ではありませんし、元々ガンマ曲線で近似してるだけで、よほど安物でない限り、 LED と同様の補正処理で sRGBガンマ変換に近づけているはずです。
視覚特性にもそこそこ都合が良い為に互換性抜きでも今もまだ利用価値はありますが、本来の視覚特性はガンマ補正よりログ、より厳密にはロジスティック曲線に近いので、Rec2100 等の高輝度、高コントラストを実現する HDR 機材(モニタやカメラ)ではログ、またはログとガンマをハイブリッドにした補正が利用されます。
- 新たなHDR国際規格BT.2100
EOTF(Electro-Optical Transfer Function) のキーワードで検索するとこの辺りの情報が見つかるでしょう。
デメリット
ガンマ補正のかかった RGB 値のまま平均を求めると、期待する(物理的な)輝度の平均になりません。
画像処理では複数のピクセルの平均輝度を計算したい事が、リサイズや回転等の座標変換やブラー等の畳み込み、グレイスケール化を含めた色変換でもあるので困ります。
 |
この図は 0〜100の階調の輝度があるとして、100 と 0 の真ん中の輝度が欲しい時、そのまま計算すると50ですが、本当の輝度平均は 73 辺りです。50 の値で表示すると輝度が20%程になる事を示しています。
実際の輝度よりも相当暗くなります。
ですので、輝度の値を計算する際には、
- ガンマ補正を外してグラフの明度(R,G,Bの値)と輝度を比例(リニア)の関係にする
- やりたい輝度計算をする。(グレイスケールだとR,G,Bを混ぜる計算)
- その後またガンマ補正をかけ直して元に戻す
といった処理を検討するべきでしょう。
- グレースケール画像のうんちく - RGB平均 (ガンマ補正)
| 元画像 | BT.709(ガンマを解除しない場合) | BT.709(ガンマ補正し直す場合) |
|---|---|---|
 |
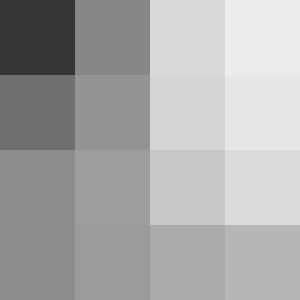 |
 |
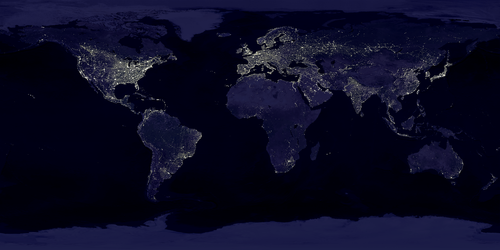
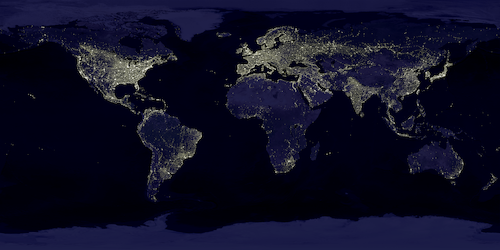
- ImageMagick リサイズ補間アルゴリズム -colorspace RGB (ガンマ補正の考慮)
| sRGB のままリサイズ | gamma:1 にしてリサイズ |
|---|---|
 |
 |
sRGB のガンマ補正
RGB の値が物理的にはどんな色なのかは規格で定められていて、現在一番メジャーなのは、sRGB です。コンピュータ上で扱う RGB は殆どこの規格に合わせた値です。(最近、iPhone の影響で P3 色空間も普及しつつあります)
この sRGB のガンマカーブは gamma:2.2 で近似される事が多いですが、厳密には低輝度で直線(linear)、高輝度で gamma:2.4の曲線(gamma curve) といった少し変則的な式を持ちます。
v = 12.92 * lv; // v <= 0.0031308
v = 1.055 * Math.pow(lv, 1/2.4) - 0.055; // v >= 0.0031308
x:0 での傾きを緩めた方が計算誤差が紛れ込みにくい、計算処理上の理由です。
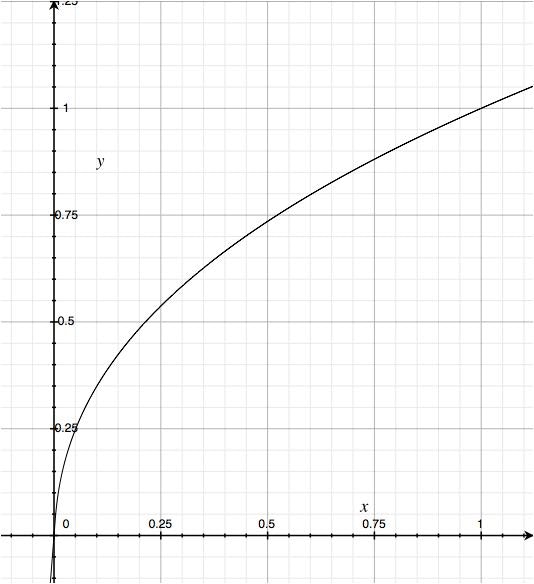 |
低輝度を主に横に拡大して、補助線を曲線の赤と直線の青で引いてみました。
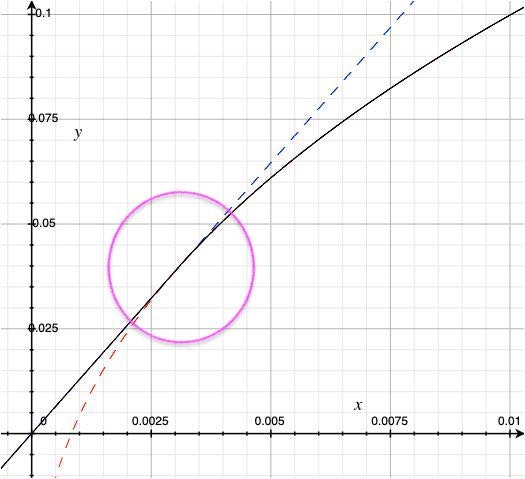 |
マゼンタの丸印のところで線形からガンマ曲線に切り替わります。
全体としては gamma:(1/2.2) に近いので、ガンマ補正を解除する時には、(1/2.2) で雑に処理する事もありますが、低輝度も厳密に処理したいのであれば規格どおりに切り替えて計算した方が良いでしょう。
注意点
ガンマ補正は浮動小数点の冪乗関数(pow)を用いるので計算負荷がそこそこ高いです。
また、色深度が 8ビット, 256階調のまま sRGB からリニアに変換すると、低輝度の階調が潰れてしまいます。具体的には sRGBの 6 以下がリニアでは 0 になります。実装によっては 20 以下がごっそり 0 になる事もあります。16ビットか、せめて12ビット以上の色深度で処理する必要があります。
- (参考) Python でグレースケール(grayscale)化 - sRGBの ガンマ補正
CPU、メモリ共に負担が増えがちな事から、現実問題としてガンマ補正による輝度の歪みに目を瞑る事も多いようです。
最後に
画像ファイルを渡して任意のガンマ補正をかけられるツールを用意しました。お試し下さい。
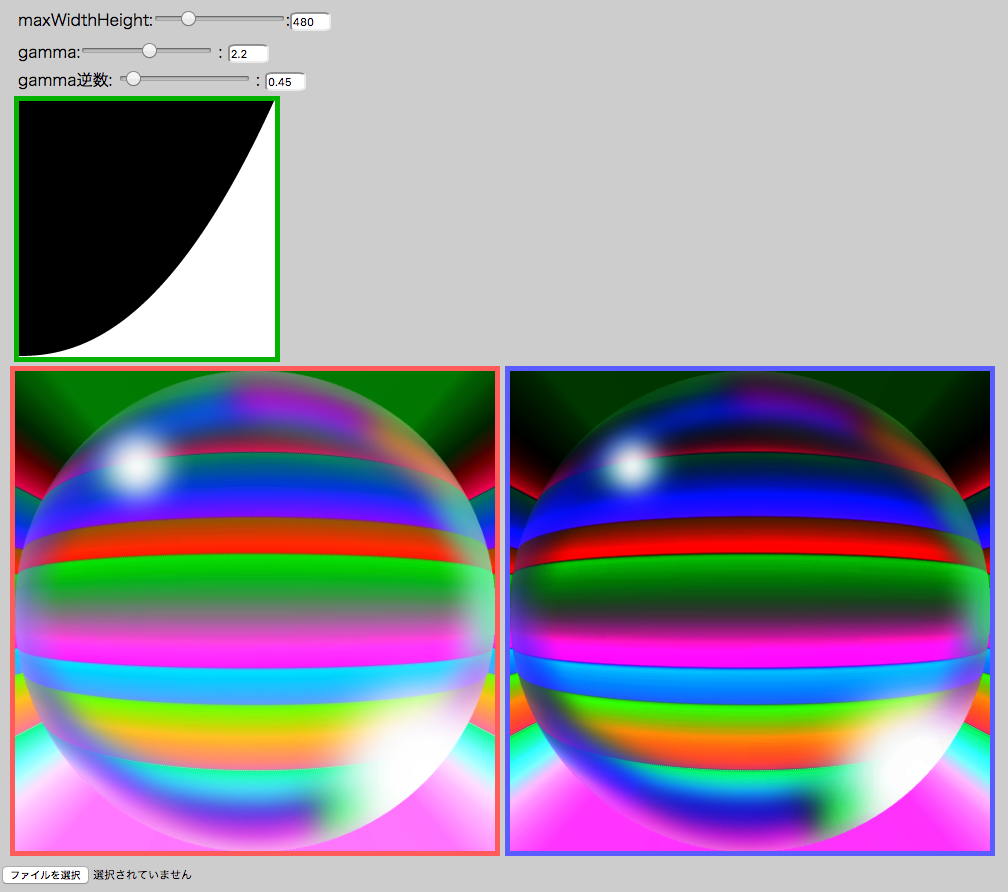 |
参考
- https://en.wikipedia.org/wiki/Gamma_correction
- https://en.wikipedia.org/wiki/SRGB
- リニアRGBのうんちく
- LED - 浜松ホトニクス
- ガンマについて
- Inigo Quilez :: articles :: gamma correct blurring - 2015
- 物理ベースレンダリング -リニアワークフロー編