はじめに
シリーズ第3回です。
前回はニューラルネットワークが、与えられた10個の数値の平均と標準偏差を出力するように学習できることが確認できました。
今回は、正規分布データを与えて、正規分布の元となっている3つのパラメーターを出力するように学習できるかどうかを試します。
正規分布
正規分布はたった3つのパラメーターからできています。ここでは3つのパラメーターを、µ、σ、kとします。
- µは、正規分布の中心軸のx座標
- σは正規分布がどれくらい幅広い分布であるかの尺度
- kは縦方向にどれくらい拡大するかの倍率
正規分布の一般式は、
y=k \times\frac{1}{\sqrt{2\pi\sigma^2}}exp{\left(-\frac{
(x - \mu)^2
}{
2\sigma^2
}\right)}
です。式をにらめば、3つのパラメータの意味が(すくなくともkとµについては)見えてくるかと思います。
この式をpythonで使えるようにしておきます。
import math
# 関数fを定義します。
f = lambda x,mu,sigma,k: k * (math.exp(-(x - mu)**2/2/sigma**2)) / math.sqrt(2*math.pi*sigma**2)
学習用データの生成
データを50,000個を、以下のように生成することにしました。3つのパラメータは以下のように幅を持たせたランダムな値です。
- x座標を0から10、
- σを0.1から2
- µを3から7
- kを0.5から10
まずx座標について0から10の間を100分割することにし、ndarrayを作ります。
import numpy as np
n = np.linspace(0, 10, 100)
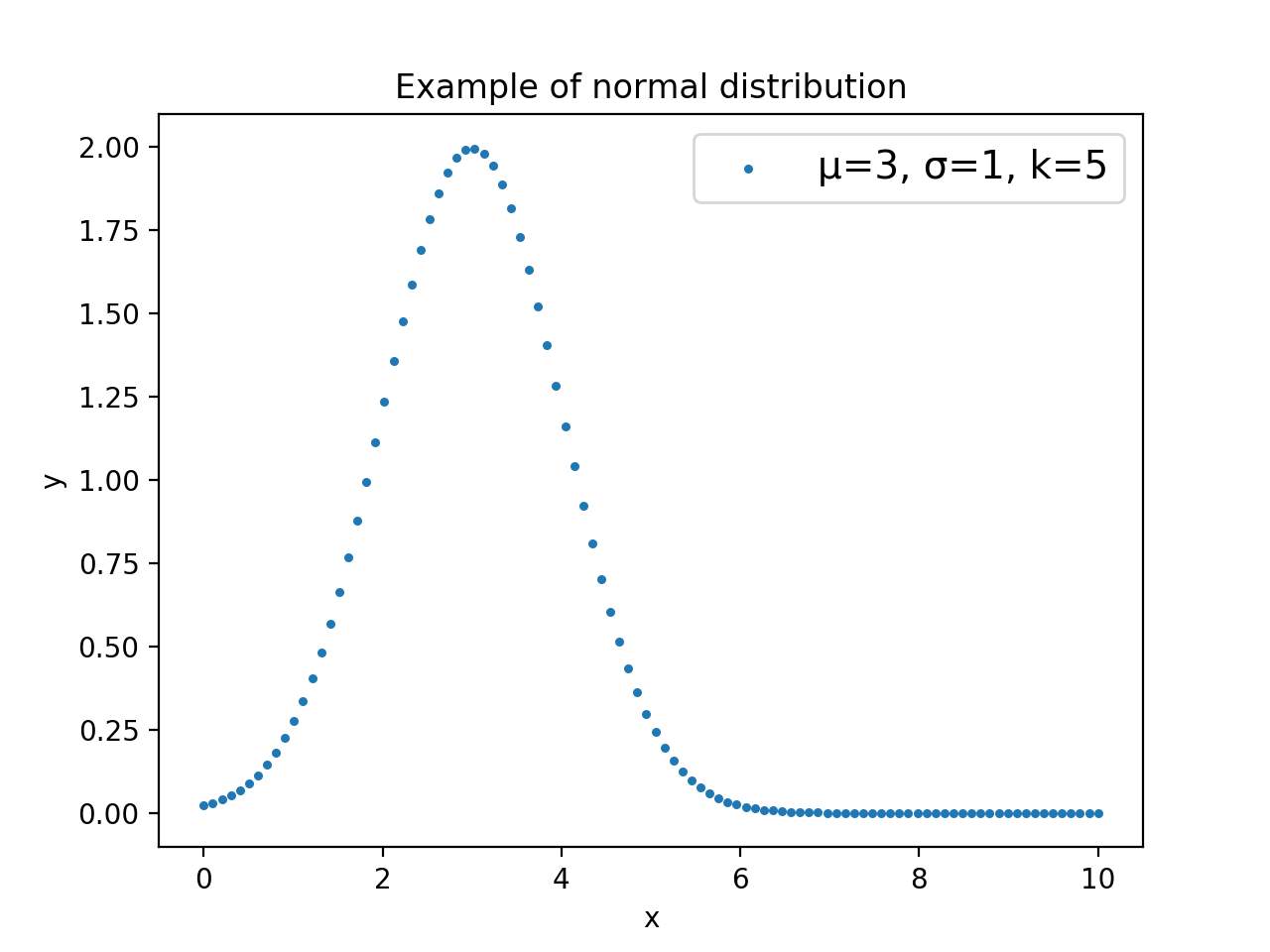
イメージが湧くように、波形データを一つ作って見ます。特に理由はありませんが、µ=3、σ=1、k=5としてみました。
import matplotlib.pyplot as plt
exampleData = []
for i in range(len(n)):
exampleData.append(f(n[i],3, 1, 5))
plt.title("Example of normal distribution")
plt.scatter(n, exampleData,label = "µ=3, σ=1, k=5",marker='.', s=20,alpha=1)
plt.legend(fontsize=14) # 凡例を表示
plt.xlabel("x")
plt.ylabel("y")
plt.show()
NNに放り込むのは100個の数値データです。離散データであることがわかるようにするため、ここではscatter plotにしました。
それでは、実際に学習に使うデータの生成です。リストを2つ作って、学習用のデータと正解データを格納します。
p = []
y = []
for kkk in range(50000):
mu1 = np.random.rand()*4 + 3 #ランダムに値を決める。3から7
si1 = np.random.rand()*1.9 + 0.1 #ランダムに値を決める。0.1から2
k1 = np.random.rand()*9.5 + 0.5 #ランダムに値を決める。0.5から10
y .append(mu1)#正解データを記録
y .append(si1)#正解データを記録
y .append(k1)#正解データを記録
for i in range(len(n)):
p.append(f(n[i],mu1, si1, k1))#定義した関数fに、x座標の値と3つのパラメータを渡し、返り値をリストpに格納。
NNに放りこむために、リストをndarrayに変え、さらに、shapeを変更します。
# ndarrayにして、shapeを変更します。
t = np.array(p)
t = t.reshape(50000,len(n))
label = np.array(y)
label = label.reshape(50000,3)
データを前半40000と後半10000に分けます。前半はトレーニング用、後半は評価用です。
# 前半40000でトレーニング。後半10000で評価。
d_training_x = t[:40000,:]
d_training_y = label[:40000,:]
d_test_x = t[40000:,:]
d_test_y = label[40000:,:]
kerasを使ったNNのデザイン
以下が最適かわかりませんが、5枚の全結合層をつなぎました。出力数を徐々に絞っていって、最後に3個の数値を出力するようにします。
import keras
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
batch_size = 128 # 訓練データを128ずつまとめて学習させる
epochs = 20 # 訓練データを、何周学習するか
model = Sequential()
model.add(Dense(100, activation='linear', input_shape=(len(n),)))
model.add(Dense(100, activation='tanh'))
model.add(Dense(40, activation='linear'))
model.add(Dense(20, activation='tanh'))
model.add(Dense(3, activation='linear'))
# 確率的勾配降下法 Adam
optimizer = Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
# 損失関数 二乗平均誤差
model.compile(loss='mean_squared_error',optimizer=optimizer)
model.summary()## NNの形状を確認
トレーニング
トレーニング開始です。fit()の返り値を変数historyに格納して、あとで学習の進行状況をグラフにします。
# 学習
history = model.fit(d_training_x, d_training_y,
batch_size=batch_size,
epochs=100,
verbose=1,# verbose..冗長、おしゃべり
validation_data=(d_test_x, d_test_y))
学習の様子の可視化
学習がどのように進んだのかグラフ化してみます。
# グラフの描画
import matplotlib.pyplot as plt
plt.plot(history.history['val_loss'], label = "val_loss")
plt.plot(history.history['loss'], label = "loss")
plt.legend() # 凡例を表示
plt.title("Can NN learn to calculate normal distribution?")
plt.xlabel("epoch")
plt.ylabel("Loss")
plt.show()
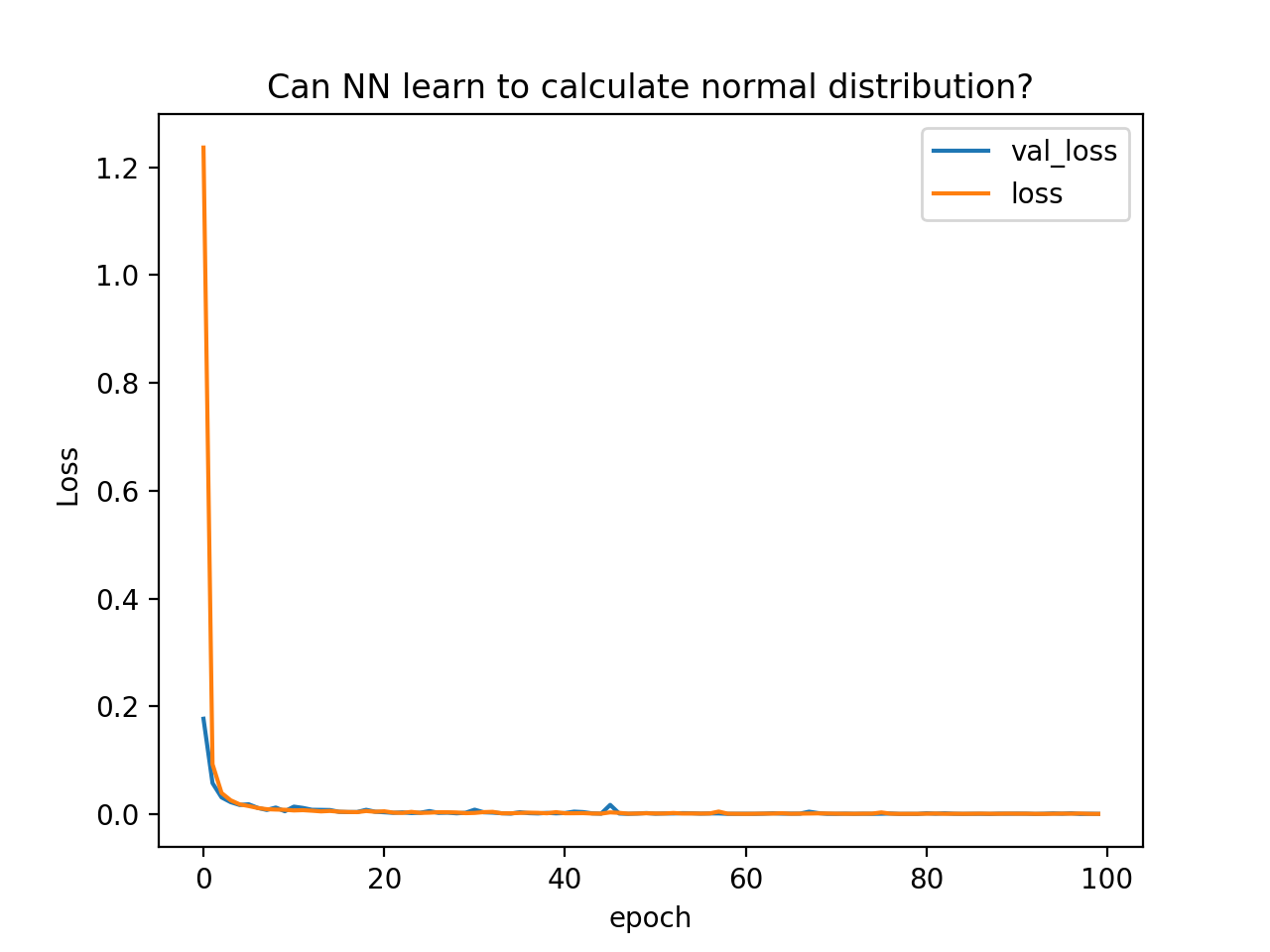
縦軸Lossは、正解データとNNからの出力データがどの程度異なっていたかについての二乗和誤差です。トレニーングに使用したデータに対してのlossと、評価用データを使って予測させた時のval_lossの2つをプロットしています。
NNの評価
トレーニングしたNNに評価用データを与えてみます。
# トレニーングしたNNにデータを与えてみる
inp = d_test_x[:200,:]
out = d_test_y[:200,:]
pred = model.predict(inp, batch_size=1)
出力をグラフにしてみます。
plt.title("Can NN learn to calculate normal distribution?")
plt.scatter(out[:,0], pred[:,0],label = "µ",marker='.', s=20,alpha=0.3)
plt.scatter(out[:,1], pred[:,1],label = "σ",marker='.', s=20,color="green",alpha=0.3)
plt.scatter(out[:,2], pred[:,2],label = "k",marker='.', s=20,color="red",alpha=0.3)
plt.legend(fontsize=14) # 凡例を表示
plt.xlabel("expected value")
plt.ylabel("prediction")
plt.show()
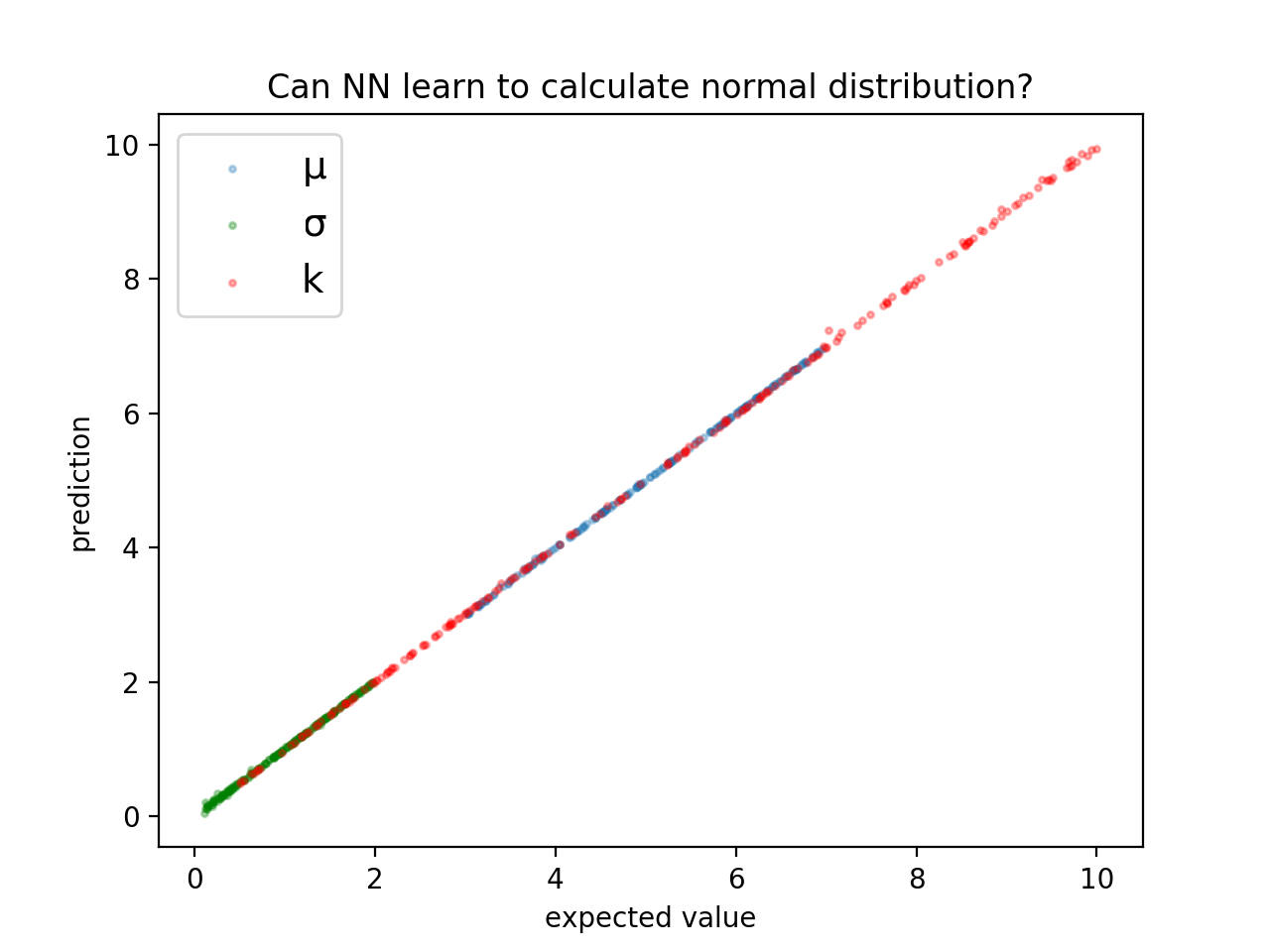
正解値と、NNからの出力がかなり近いことがわかります。つまり、ちゃんと学習できました。
まとめ
重なっていて見にくいですが、3つのパラメーターともかなり正しく出力できています。できました!
シリーズ第1回 準備編
シリーズ第2回 平均と標準偏差
シリーズ第3回 正規分布
シリーズ第4回 円