はじめに
シリーズ第2回です。
与えられたいくつかの数値データについて、その平均を出力するように、ニューラルネットワーク(NN)に学習させることはできるでしょうか?また、標準偏差はどうでしょうか?やってみましょう。
NNが学習できる問題は、大きく分けて「分類問題」か「回帰問題」であるとされています。今回は「回帰問題」にあたります。
方針
- ニューラルネットワークに10個(固定)のランダムな数字を与える。
- 10個の数字の平均と、標準偏差を、計算する。
- 10個の数字と、これらの平均と標準偏差を、学習データとして、kerasで作成したNNに与える。
- NNの出口の数は2(「平均」と「標準偏差」の2つ)。
- NNをトレーニングした後、学習に用いたのではないデータセットを使って学習させたNNの性能評価を行う。
ではやってみましょう。一般的にNNのトレーニングは学習データの準備が大変とされていますが、その点今回は準備が楽です。
学習データの準備
とりあえず、50000個のトレーニング用データセットを準備することにしました。1セットは10個の数値よりなります。10個の数値は、numpyのrandom.normal(a,b,10)を使用して平均a、標準偏差bの分布データに従う10個のランダムな数値としますが、ここで、aとb自体もnumpyのrandom.rand()で発生させています。
「10個の数値」、および「これらの平均と標準偏差」を計算して、まずはそれぞれリストに格納します。
import numpy as np
trainDataSize = 50000 #作成するデータセットの数
dataLength = 10 #1セットあたりのデータ数
d = []#空のリスト 10個ずつ数値を入れる。
average_std = []#空のリスト 2つ目。2つずつ数値を入れる。
for num in range(trainDataSize):
xx = np.random.normal(np.random.rand(),np.random.rand(),dataLength)
average_std.append(np.mean(xx))
average_std.append(np.std(xx))
d.append(xx)
50000セット全部入れたリストができたら、あらためてndarrayに変換します。
d = np.array(d) # ndarrayにする。
average_std = np.array(average_std)# ndarrayにする。
なぜ最初からndarrayにしないかといえば、遅いからです。
# 良くないコード。遅いから。
d = np.array([])#空のnumpy array
for num in range(trainDataSize):
xx = np.random.normal(np.random.rand(),np.random.rand(),dataLength)
d = np.append(d,xx) #この処理が遅い!
作成したndarrayは、順番に数値データを放り込んだものです。ここで行列のshapeを変えます。
d = d.reshape(50000,10)
average_std = average_std.reshape(50000,2)
50000のデータセットを、トレーニング用の40000セットと評価用の10000セットの2つに分割。今回ハイパーパラメーターの検討はしないので、2分割で良いことにする。
# 前半40000でトレーニング。後半10000で評価。
d_training_x = d[:40000,:]
d_training_y = average_std[:40000,:]
d_test_x = d[40000:,:]
d_test_y = average_std[40000:,:]
NNのデザイン
ポイントは、
- 入力のshapeを10にする(必須)
- 最後のレイヤーの出力数を2にする(必須)。
- 最後の活性化関数をlinearにする。今回のケースではsoftmaxとかsigmoidとかReLuはそぐわない。平均が0を下回るケースがあるため。
- 損失関数をmean_squared_errorにする。クロスエントロピーはこの場合そぐわない(分類問題ではないから)。
- その他レイヤーの数、各レイヤーの出力数と活性化関数は、適当に決定した。
import keras
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
model = Sequential()
model.add(Dense(100, activation='tanh', input_shape=(10,)))#入力スロットは10個。
model.add(Dense(100, activation='tanh'))
model.add(Dense(40, activation='sigmoid'))
model.add(Dense(20, activation='sigmoid'))
model.add(Dense(2, activation='linear')) #出力スロットは2つ。
# 確率的勾配降下法 Adam
optimizer = Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
# 損失関数 二乗平均誤差
model.compile(loss='mean_squared_error',optimizer=optimizer)
model.summary() # NNの概要の出力
NNのトレーニング
いよいよ訓練データを放り込みます。
history = model.fit(d_training_x, d_training_y,
batch_size=256,# 訓練データを、256セットデータ分をまとめて放り込む。
epochs=20,# 訓練データを、何周繰り返すか。
verbose=1,# verboseは冗長、転じて「おしゃべり」の意。1にしておくとトレーニング過程を逐一出力してくれる。
validation_data=(d_test_x, d_test_y))
学習の進み具合の確認
ここではfit()の返り値を、変数historyにしまっています。返り値historyをtype()で調べると、オブジェクトのようです。vars()で調べてみます。
type(history) # <class 'keras.callbacks.callbacks.History'>
vars(history)
# 情報がたくさん出力される。
# 出力される情報をかいつまむと、historyオブジェクトが持っているフィールドは、以下の通り。
# validation_data (リスト)、
# model (NNモデルへの参照)、
# params (辞書。keyは'batch_size'、'epochs'、'steps'、'samples'、'verbose'、'do_validation'、'metrics')
# epoch (リスト)、
# history (辞書。keyは'val_loss'、'loss')
#
# historyのkeyは、'val_loss'と'loss'である。
# lossは学習データに対する損失。val_lossは評価用のデータに対する損失。ここでは変数名がhistoryなので、history.history['val_loss']で、学習がどう進んだかの経過データにアクセスできる。
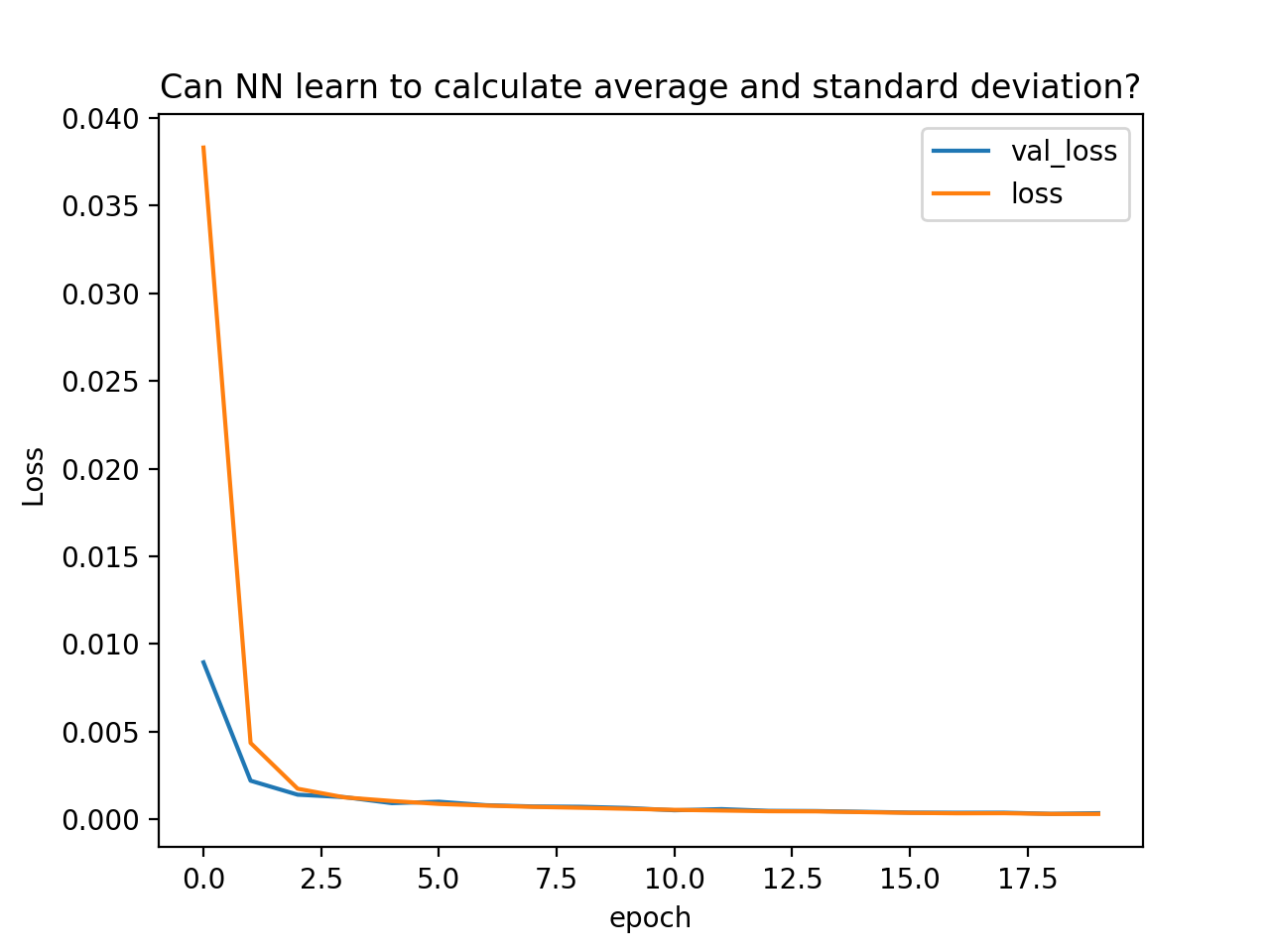
学習が進行する様子をプロットしてみる。
import matplotlib.pyplot as plt
plt.plot(history.history['val_loss'], label = "val_loss")
plt.plot(history.history['loss'], label = "loss")
plt.legend() # 凡例を表示
plt.title("Can NN learn to calculate average and standard deviation?")
plt.xlabel("epoch")
plt.ylabel(" Loss")
plt.show()
NNの評価
学習が進行したことはわかりますが、どれほど精度良く「計算」できるようになったでしょうか?評価用データの先頭200セットをNNに放り込んで、その出力(縦軸)を数学的な計算結果(横軸)に対してプロットしてみる。
# トレニーングしたNNにデータを与えてみる
inp = d_test_x[:200,:]
out = d_test_y[:200,:]
pred = model.predict(inp, batch_size=1)
# グラフにする: 平均
plt.scatter(out[:,0], pred[:,0])
plt.legend() # 凡例を表示
plt.title("average")
plt.xlabel("mathematical calculation")
plt.ylabel("NN output")
# 線を引く。この線に乗れば、うまく予測できたことになる。
x = np.arange(-0.5, 2, 0.01)
y = x
plt.plot(x, y)
plt.show()
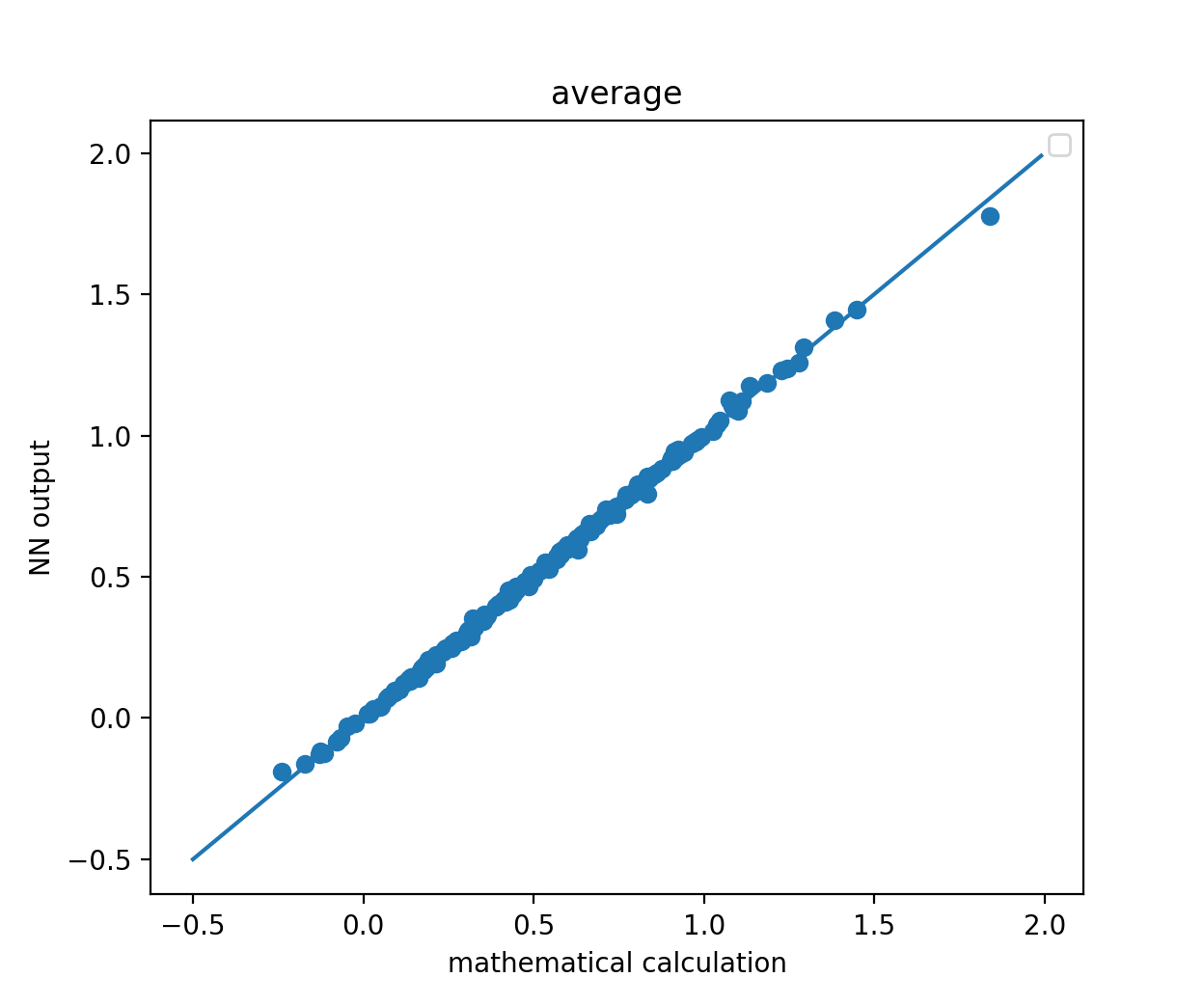
おおよそ精度良く「計算」できていることがわかります。続いて、標準偏差はどうでしょうか?
# グラフにする: 標準偏差
plt.scatter(out[:,1], pred[:,1])
plt.legend() # 凡例を表示
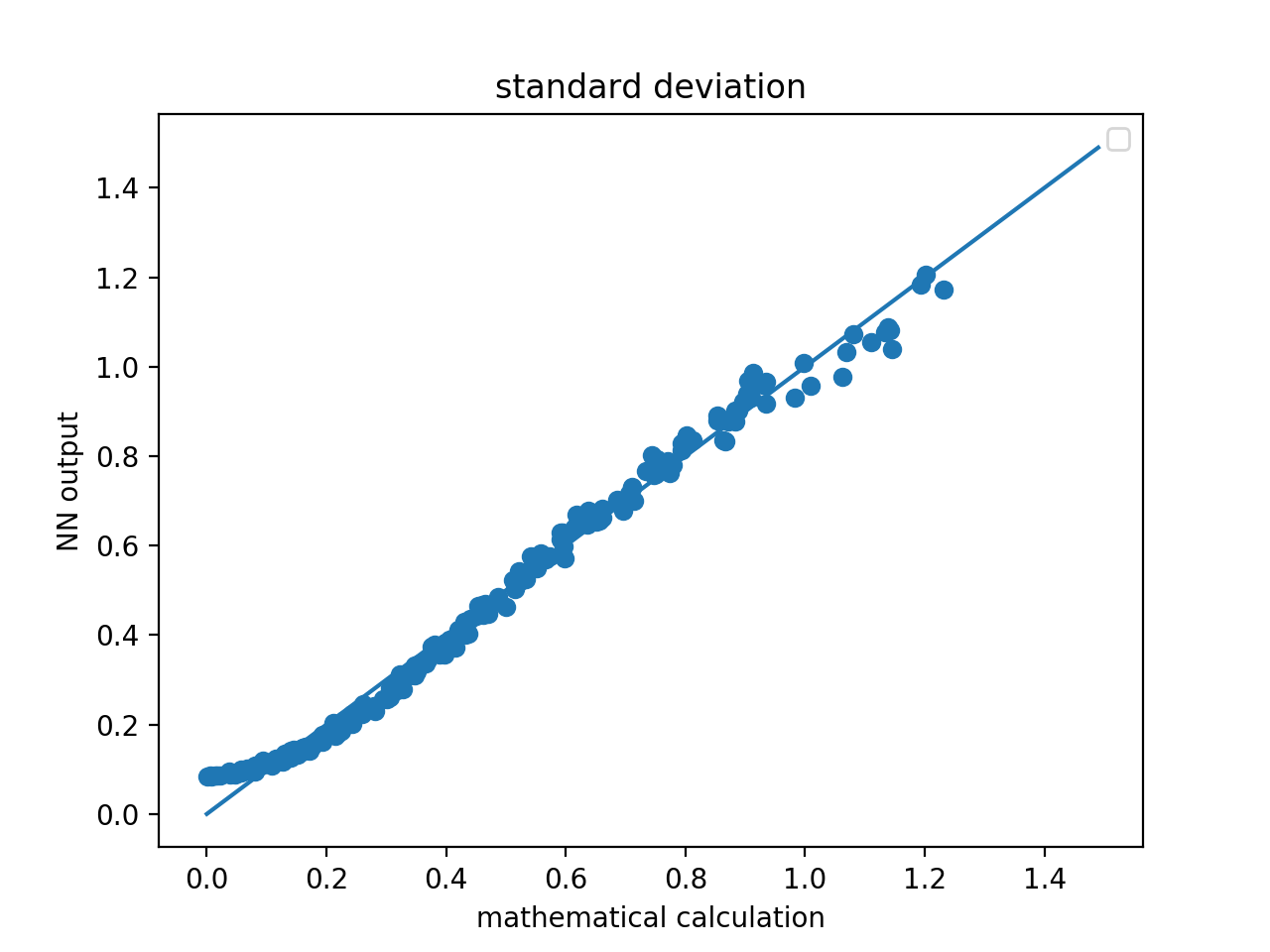
plt.title("standard deviation")
plt.xlabel("mathematical calculation")
plt.ylabel("NN output")
x = np.arange(0, 1.5, 0.01)
y = x
plt.plot(x, y)
plt.show()
まずまずといったところでしょうか?平均の方は良いとして、標準偏差は今ひとつ物足りません。
考察
ニューラルネットワークで行われる計算は、ざっくりといえば入力値xに対して各ウエイトパラメーターwを掛け合わせた積を得ること、この積の和を活性化関数の入力として出力値を得ること、です。
平均については、入力値それぞれに0.1 (今回の場合入力する数値が10個なので1/10 = 0.1)をかけて足し合わせれば平均になりますので、NNが10個の数値の平均を精度良く計算できるようになることは、容易に想像ができます。
一方で標準偏差はどうでしょうか?平均値を計算し、ついで入力値それぞれに、平均値に-1をかけたものを足して(つまり、平均との差をとって)、これを2乗して足し合わせて、9で割れば、標準偏差になるはずです。このプロセスで、難しそうなのは、2乗するところです。
NNでは内部的に、固定のウエイトパラメータと入力値の掛け算をおこない、これを足し合わせて活性化関数に渡しています。任意の入力値に対して、これを2乗した値をほとんど誤差がないように返すことは果たして可能なのか?パラメーターを増やせばどんな曲線も表現できるはずですが、どんな計算になるのかちょっと私にはわかりません。
もしかすると、活性化関数に、入力値を2乗(拡張してn乗)してくれるやつがあったりすれば良いのかもしれませんね。これについてはどこかで考えてみたいと思います。
まとめ
平均と標準偏差に近い値を出力できるNNができたということで、第2回は終了したいと思います。
シリーズ第1回 準備編
シリーズ第2回 平均と標準偏差
シリーズ第3回 正規分布
シリーズ第4回 円