はじめに
千葉大学・株式会社Nospareの川久保です.
今回は,回帰モデルのうち,目的変数が連続変数ではなく,カウントだったり二値変数だったりする場合のモデルを含んだ一般化線形モデル(Generalized Linear Model, GLM)について解説します.また,GLMに変量効果を導入した一般化線形混合モデル(Generalize Linear Mixed Model, GLMM)も解説します.
一般化線形モデル(GLM)
線形モデル(LM)のおさらい
目的変数 $y_i \ (i=1,\dots,n)$ を説明変数 $x_i = (x_{i1},\dots,x_{ip})^\top$の線形結合で説明することを目的とした,
$$
y_i = x_i^\top \beta + \varepsilon_i, \quad \varepsilon_i \overset{\mathrm{iid}}{\sim} (0,\sigma^2), \tag{1}
$$
というモデルを,線形回帰モデル,もしくは単に線形モデル(Linear Model, LM)と呼びます.ここで,$\varepsilon_i$は平均$0$,分散$\sigma^2$の連続分布にしたがうとしますが,回帰係数の有意性検定としてt検定などやF検定を行う場合は,暗に$\varepsilon_i$に正規分布を仮定しています.LM(1)は以下のように書き換えることができます.
$$
E[y_i] = x_i^\top \beta, \quad V(y_i) = \sigma^2, \tag{2}
$$
(2)の表現は,$y_i$の平均に$x_i^\top \beta$という構造を入れていると解釈できるので,通常の線形回帰モデルは平均回帰(mean regression)とも呼ばれます.回帰モデルにはmean regressionの他,median regression, その一般化としてのquantile regression(分位点回帰),mode (modal) regressionなどがあります.分位点回帰については,小林先生の一連の記事([R]quantregパッケージで分位点回帰をしてみる,[R]分位点回帰をベイズ推定してみる,[R]打ち切りのある分位点回帰モデルをベイズ推定する)をぜひご覧ください.
LMではまずいケース
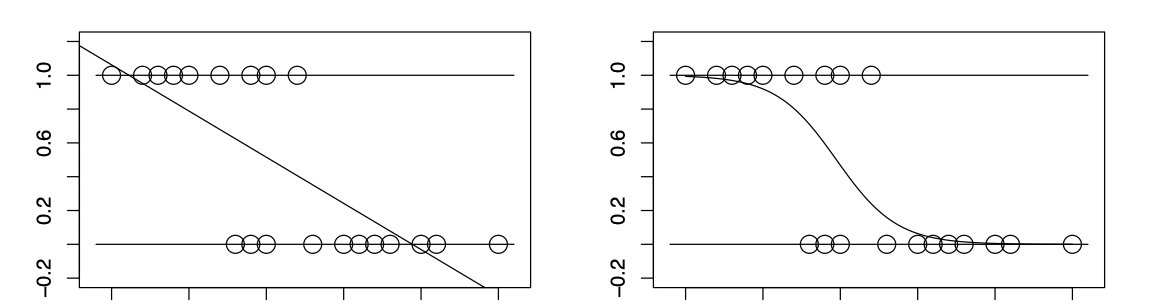
$y_i$が0か1の二値をとる変数に, LMを当てはめるとまずいことがおきます.(2)の表現で考えてみます.いま$y_i$は二値変数(ベルヌーイ確率変数)なので,その平均$E[y_i]$は0から1の間の値をとります.しかし$x_i^\top \beta$は実数全体を取り得るため,このままでは(2)のモデルは不適切です.左図では,当てはめた回帰直線が$x$の値によっては負の値になったり1を超えたりしていますが,これは$y_i = 1$となる確率の当てはめ値としては明らかに不適切です.そこで直線ではなく右図のような曲線を当てはめることを考えます.同様に,$y_i$としてポアソン分布のようなカウントを考えると,その平均$E[y_i]$は正の値をとるため,やはりLMでは不適切です.
リンク関数を用いた回帰
$y_i$として二値変数やカウントを考える場合,その平均構造に$x_i^\top \beta$を仮定することが不適切であることを見てきました.そこで,平均$E[y_i]$に何らかの変換を施して,変換したものと$x_i^\top \beta$を結びつけることを考えます.この変換を施す関数をリンク関数と呼びます.リンク関数を$g(\cdot)$,その逆関数を$g^{-1}(\cdot)$とすると,
$$
E[y_i] = g^{-1}(x_i^\top \beta), \tag{3}
$$
という構造を入れることを考えるわけです.(3)式のモデルを,一般化線形モデル(Generalized Linear Model, GLM)と呼びます.
リンク関数としては,変換を施すことで実数全体に引き延ばされるような関数を導入します.
$y_i$としてカウントを考えると,$E[y_i]$は正の実数をとるため,リンク関数としては正の実数から実数全体に写すような関数を仮定します.よく用いられるのは対数関数で,$g(\cdot) = \log(\cdot)$,その逆関数は指数関数$g^{-1}(\cdot) = \exp(\cdot)$です.
$y_i$として二値変数を考えると,$E[y_i]$は0から1の間の実数をとり,2つのリンク関数がよく用いられます.1つはロジット関数で,
$$
g(p) = \log\left( {p \over 1-p} \right)
$$
という形をとります.この逆関数は
$$
g^{-1}(x) = {\exp(x) \over 1 + \exp(x)}
$$
で,ロジスティック関数と呼ばれます.このリンク関数を用いたGLMのことを,ロジスティック回帰モデル,もしくはロジットモデルと呼びます.もう1つは$g^{-1}(\cdot)$として標準正規分布の累積分布関数を用いるというもので,プロビット(回帰)モデルと呼ばれています.標準正規分布の累積分布関数は陽に書けません.
GLMの推定
パラメータ推定は,頻度論では最尤法が基本ですが,分布の特定を避けるために疑似尤度も用いられます.
ベイズ推定する場合は,事後分布からのサンプリングを容易にしたいというモチベーションがあります.プロビットモデルにおいてはデータ拡大(deta augmentation)法を用いることによって完全条件付分布(full conditional distribution)の共役性を利用でき,容易にギブスサンプリングが実行できます.一方,ロジットモデルでは,近年Polya-Gamma mixtureという表現方法を用いることで,完全条件付分布の共役性が達成されギブスサンプリングが容易に実行できる方法が導入されました.詳しくは,小林先生の記事(ロジットモデルに対するギブスサンプリングを簡単に行う!(理論編),ロジットモデルに対するギブスサンプリングを簡単に行う!(R編))をご覧ください.
一般化線形混合モデル(GLMM)
GLMに変量効果を導入してGLMMに
以前の記事で,線形回帰モデルに変量効果を導入した線形混合モデル(Linear mixed model, LMM)を紹介しました.今回説明したGLMに変量効果を導入すると,一般化線形混合モデル(GLMM)と呼ばれるモデルのクラスになります.LMMの記事でも紹介した,クラスターデータの応用例に即して説明します.
$y_{ij} \ (i=1,\dots,n; j = 1,\dots,n_i)$を$i$番目のクラスターにおける$j$番目の観測とします.共変量$x_{ij}$が利用可能であるとき,
$$
E[y_{ij} \mid b_i] = g^{-1}(x_{ij}^\top \beta + z_{ij}^\top b_i), \quad b_i \sim \mathrm{N}(0,\sigma^2) \tag{4}
$$
というモデルを考えます.$g(\cdot)$はリンク関数で,$y_{ij} \mid b_i$の平均パラメータを実数全体に写すための関数で,(3)式のGLMのときと同じ役割です.リンク関数が恒等関数の場合,GLMMはLMMになります.GLMとGLMMの違いは,GLMMには変量効果$b_i$が入っている点です.クラスターデータの場合,$b_i$はクラスター$i$の個別効果をあらわします.
LM, LMM, GLM, GLMMの違い
これまで説明してきた4つのモデルの比較を表にまとめると以下のようになります.
| 変量効果なし | 変量効果あり | |
|---|---|---|
| リンク関数が恒等関数 | LM | LMM |
| リンク関数が恒等関数でない | GLM | GLMM |
GLMMのパラメータ推定
GLMMのパラメータ推定を尤度関数にもとづいて行う場合,変量効果$b_i$を積分消去した$y$の周辺尤度を考える必要があります.しかしながら,リンク関数が恒等関数で正規分布を仮定したLMMの場合を除き,積分の評価が困難で尤度関数を陽に書けません.そこで,数値積分を使う方法,近似的な尤度を用いる方法,EMアルゴリズムなど,様々な方法が提案されています.
データ解析例
以前の記事のLMMのデータ解析例でも用いたlme4というパッケージを使って,GLMMのデータ解析を実行してみます.lme4内のgrouseticksという,ライチョウ(grouse)に付着したダニ(ticks)の数のデータセットに,ポアソン回帰を当てはめます.変量効果の入ったポアソン回帰(GLMMの一種)をlme4のglmer()関数を使って,変量効果の入っていないポアソン回帰(GLMの一種)をRのstatsパッケージ(起動時に自動的に読み込まれる)のglm()関数を使って,推定を行います.
library(lme4)
fit_GLM <- glm(TICKS ~ YEAR, family = poisson(), data = grouseticks)
fit_GLMM <- glmer(TICKS ~ YEAR + (1 | LOCATION), family = "poisson", data = grouseticks, nAGQ = 25)
ライチョウの個体ごとのダニの数TICKS(カウントデータ)を目的変数,ダミー変数としての観測年YEARを(固定効果の)説明変数としています.またGLMMでは,変量効果として観測地点LOCATIONの効果を入れています.glmer()におけるformulaの書き方は,LMMのときに用いたlmer()のものと同様で,(1 | LOCATION)の項がrandom interceptを表しています.(4)式のモデル表現において,$z_{ij} = 1$としたものに対応します.また,glmer()の引数nAGQは,周辺尤度を評価する際に用いるガウス・エルミート求積法(数値積分の一種)の軸ごとの評価点の個数ですが,この数が多いほど周辺尤度の評価が精確になる一方,数値計算に時間がかかります.デフォルトはnAGQ = 1に設定されており(ラプラス近似に対応),変量効果の次元が高くなると,そのような設定でないと現実的な時間での推定が難しくなりますが,今の例では変量効果は一次元ですので,nAGQ = 25とマニュアル上で推奨されている値を用います.
結果のサマリーは以下です.まずGLMの結果です.
> summary(fit_GLM)
Call:
glm(formula = TICKS ~ YEAR, family = poisson(), data = grouseticks)
Deviance Residuals:
Min 1Q Median 3Q Max
-4.7110 -2.8888 -1.5183 0.7139 17.1467
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.78318 0.03790 47.05 <2e-16 ***
YEAR96 0.62348 0.04492 13.88 <2e-16 ***
YEAR97 -1.64109 0.08977 -18.28 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 5847.5 on 402 degrees of freedom
Residual deviance: 4549.4 on 400 degrees of freedom
AIC: 5486.4
Number of Fisher Scoring iterations: 6
次にGLMMの結果です.
> summary(fit_GLMM)
Generalized linear mixed model fit by maximum likelihood
(Adaptive Gauss-Hermite Quadrature, nAGQ = 25) [glmerMod]
Family: poisson ( log )
Formula: TICKS ~ YEAR + (1 | LOCATION)
Data: grouseticks
AIC BIC logLik deviance df.resid
1374.8 1390.8 -683.4 1366.8 399
Scaled residuals:
Min 1Q Median 3Q Max
-6.6401 -0.8847 -0.4704 0.8549 5.5755
Random effects:
Groups Name Variance Std.Dev.
LOCATION (Intercept) 1.662 1.289
Number of obs: 403, groups: LOCATION, 63
Fixed effects:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.64907 0.18549 3.499 0.000467 ***
YEAR96 0.94352 0.08529 11.063 < 2e-16 ***
YEAR97 -1.43669 0.12362 -11.622 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Correlation of Fixed Effects:
(Intr) YEAR96
YEAR96 -0.293
YEAR97 -0.238 0.521
GLMとGLMMで,固定効果の回帰係数Intercept,YEAR96,YEAR97の推定値の符号に変化があるなどの大きな結果の違いはありませんが,GLMMの変量効果の分散が1.662と推定されており,GLMMはLOCATIONの効果をとらえた推定をしています.また,厳密な分析ではありませんが,GLMMはGLMと比べてAICの値が大きく減少していることからも,変量効果を考慮に入れたGLMMが良さそうです.なぜ厳密でないかは,変量効果の分散が0の状況(GLMに対応)は,パラメータ空間の内点でないため,AICの導出で使用するテイラー展開のテクニックが正当化できないためです.
おわりに
株式会社Nospareには,統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.