[R] quantregパッケージで分位点回帰をしてみる

こんにちは，株式会社Nospareリサーチャー・千葉大学の小林です．本記事では分位点回帰モデルという回帰モデルの一種について取り上げます．分位点回帰を使うことで通常の回帰モデルよりも被説明変数（の分布）と説明変数の間の関係をより詳細に調べることができます．

まず通常の回帰モデルについて

回帰モデルは説明変数$x$の値が変化したときに被説明変数$y$の値ががどのように変化するのかを調べるためによく使われ，以下のような形式で表されます．

y_i=x_i'\beta + \epsilon_i,\quad i=1,\dots,n.

ここで$\beta$は回帰モデルの係数パラメータ，$\epsilon_i$は誤差項を表します．残差平方和

\sum_{i=1}^n(y_i-x_i'\beta)^2

を最小化するように$\beta$の値を選ぶと，最小自乗推定量（OLS）が得られます．また$\epsilon_i$に正規分布$N(0,\sigma^2)$を仮定して最尤法で$\beta$を推定しても（つまり$y_i\sim N(x_i'\beta,\sigma^2)$），$\beta$の最尤推定量（MLE）はOLSと同じものになります．通常の回帰モデルは$x$が与えられたときの$y$の条件付分布の期待値（平均）の構造についてモデル化したものになります：

E[y_i|x_i]=x_i'\beta.

通常の回帰モデルはデータ分析の非常に幅広い領域で適用されてきました．しかし，あくまでも平均についてのモデルですので，

平均の構造について関心があまりない，$y$の条件分布の他の部分について関心がある
$y$の分布が対称でない
データに外れ値がある

などといった場合には，直接の適用は適切ではない場合があります．

分位点回帰モデルについて

分位点回帰モデルは$y$の条件付期待値ではなく，$y$の条件付分布の分位点（quantile）についてのモデル化を行います．$y$の$x$が与えられたときの$\tau$-条件付分位点は数学的には

Q_{y|x}(\tau) = \inf_{y \in \mathbb{R}}\{y: F(y|x) > \tau\},\ \tau \in (0,1),

と定義されます．ここで$F(y|x)$は$y$の条件付分布の分布関数です．イメージとしては$\tau=0.9$のときには分布の上側10%の点，$\tau=0.25$のときには下側25%の点（第１四分位）になります．また$\tau=0.5$のときには分位点は中央値（median regression）になります．線形分位点回帰モデルではこの条件付分位点を$x$によってモデル化し

Q_{y_i|x}(\tau)=x_i'\beta,

係数パラメータ$\beta$を次の非対称な損失関数（チェックロスと呼ばれたりします）を最小化します

\sum_{i=1}^n\rho_\tau(u_i)=\sum_{i=1}^n u_i(\tau-I(u_i<0))

ここで$u_i=y_i-x_i'\beta_\tau$，$I(\cdot)$は支持関数を表します．チェックロス（$\tau=0.1,0.5,0.75$）は次の図ような形状をしています（灰色の点線は二乗ロスを表します）．ここで$\beta_\tau$としているのは，推定する分位点レベルによって係数パラメータの値が異なる可能性があるということを表しています．よって複数の分位点において回帰モデルを推定し，係数を$\tau$の関数としてプロットさせることでそれがどのように変化していくかを視覚化することもできます．

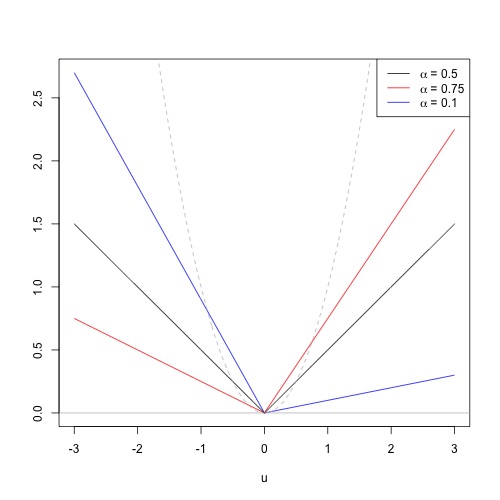
説明変数が定数項のみからなる場合にはチェックロスの最小解は$y$の標本分位点になりますが，一般的な説明変数の場合には最小化は解析的に解くことができないので，数値的に最適化を行うことになります．

分位点回帰のメリット

分位点回帰を使うことで，通常の期待値に関する回帰モデルの上述の問題点を解決することが可能になります．

平均以外のの構造について分析できる
- 売上トップ10%の顧客がマーケティング変数に対してどのように反応するのかがわかる
- 株式などの金融資産のリターンの分布の左裾（損失）について分析することでリスク評価が行える
$y$の分布が対称でなくても大丈夫
- 例えば中央値を分析することで，平均値に代わる分布の中心位置についての回帰分析ができる
データの外れ値に対して頑健
- 平均（期待値）は外れ値に敏感に反応するのに対して，中央値は外れ値に対して頑健であるのでロバストな回帰手法のひとつとして利用できる

quantregパッケージを使ってみる

分位点回帰分析に関するRのパッケージがいくつかリリースされています．まずはquantregパッケージを使ってみましょう．このパッケージで基本となるのがrq()関数で，基本的な分位点回帰モデルの推定を行います．特に設定する必要のある重要な引数としては

formula：回帰モデルの記述，通常の回帰分析で使用されるlm()関数と同様に書きます
tau：分位点のレベル，0.5がデフォルト．$(0,1)$の間の値のベクトルとしても指定できます．また$(0,1)$以外の値に指定すると，$(0,1)$の間のすべての値でモデルが推定されます
method：数値最適化手法を選択します．また"lasso"や"scad"と指定することでそれぞれLASSOやSCADに基づいた変数選択を行うことも可能です．

線形分位点回帰モデルを推定する

イメージを掴むために人工データを使ってみましょう．ここでは真の条件付分位点は$N(1+2x,1)$の分布関数の逆関数で，$\beta_{\tau,1}$の真値は$N(1,1)$の分布関数の逆関数，$\beta_{\tau,1}$の真値はすべての$\tau$の値で$2$です．まず以下のコードでは$\tau=0.1,0.5,0.9$について分位点回帰を行います．

library(quantreg)
# データを発生させる
set.seed(1)
n <- 200
x <- rnorm(n)
# Q(tau) = 1 + 2*x
y <- rnorm(n, mean=1+2.0*x)
# tauを設定
tau  <- c(0.1,0.5,0.9)
# 分位点回帰モデルを推定する
res  <- rq(y~x, tau=tau)
# 予測のためのデータを作成
x_n  <- data.frame(x=seq(-3,3,1))
# 予測を行う
pred <- predict(res, newdata=x_n)
# 描画する
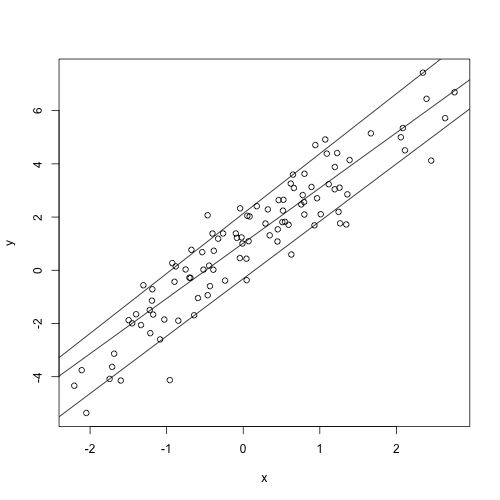
plot(y=y, x=x)
for (i in 1:length(tau))
    lines(y=pred[,i], x=x_n$x)

実行するとデータの散布図について条件付分位点が描かれます．上から順に$\tau=0.1,0.5,0.9$の値に対応しています．

同じデータを使ってもう一度推定してみます．ただし今度はtauを-1に指定することで，$\tau$を$(0,1)$の間のすべての値でモデルが推定されます．推定結果をplot()関数で描画すると$\beta_\tau$を$\tau$の関数として視覚化することができます．

# tauを-1に指定する
res <- rq(y~x, tau=-1)
# beta_tauのプロセスが描画される
plot(res, nrow=1, ncol=2)

実行するとこのような図が作成されます．

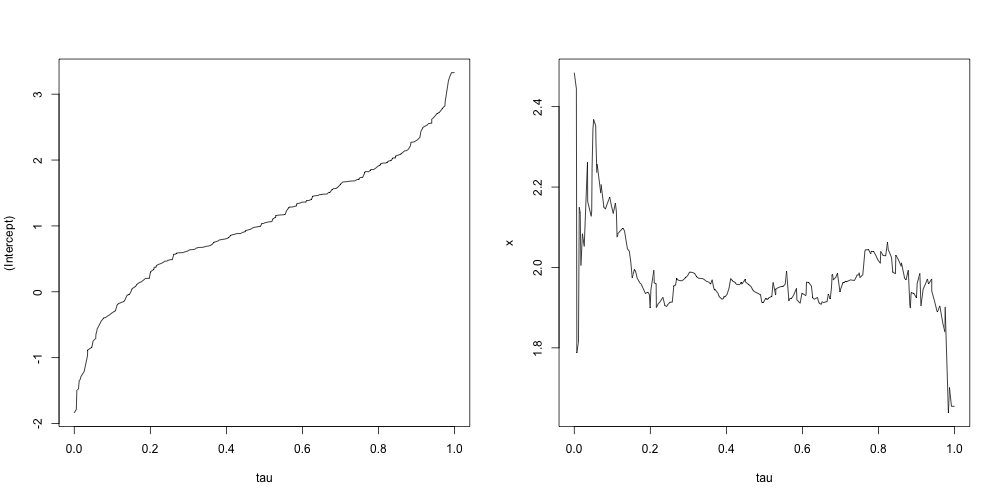
この図を見ると$\beta_{\tau,2}$の推定値は$\tau$の値が$0$か$1$に近くなると不安定になっています．サンプルサイズが小さいときには分布の裾を正確に推定することは難しいということがわかります．数値計算上の問題の部分もあるのでベイズ分位点回帰だともう少し改善される可能性があります．モデルの推定値と信頼区間はsummary()関数で表示できます．

加法モデルを推定する

quatregパッケージではnlrq()関数によって非線形モデルを取り扱うことができますが，ここでは特にノンパラメトリック加法モデルを推定するrqss()関数を紹介します．加法分位点回帰モデルにおいては一般的に次のような条件付分位点関数を考えることになります

Q_{y_i|x}(\tau)=\sum_{j=1}^pf_{\tau j}(x_{ij}) + z_i'\gamma_\tau.

ここで$f_{\tau j}$は説明変数$x_{ij}$の非線形な未知関数でノンパラメトリックに推定されます．$z_i$は$\gamma_\tau$という線形効果をもつ説明変数です．

quantregパッケージではqss()関数によってによって$f_{\tau j}$を1変数あるいは2変数の関数として指定することができ，また関数の形状に制約を課すことができます．重要な引数は

x：ノンパラメトリックな項の変数に対応するデータ．もし２列の行列が指定された場合には２変量の関数となります
constraint：関数の形状に制約を課します．次のように二重引用符で指定します．
- "N"：デフォルトでは制約は課しません
- "I"，"D"：単調増加，単調減少
- "V"，"C"：凸，凹関数
- "VI"，"VD"：単調増加凸，単調減少凸
- "CI"，"CD"：単調増加凹，単調減少凹

その他にも当てはまりの良さと滑らかさをコントロールするlambdaや関数の滑らかさについてのペナルティを関数そのものや導関数に課すDorderなどがあります．

rqss()関数では加法モデルを推定してみます．ノンパラメトリック関数の形状制約をなし，単調増加，単調増加凹の３つの場合で中央値について（$\tau=0.5$）推定します．

set.seed(1)
n <- 200
x <- sort(rchisq(n,4))
y <- log(x)+ 0.1*(log(x))^2 + log(x)*rnorm(n)/4
res_n  <- rqss(y~qss(x, constraint="N"), tau=0.5)
res_i  <- rqss(y~qss(x, constraint="I"), tau=0.5)
res_ci <- rqss(y~qss(x, constraint="CI"), tau=0.5)

plot(y=y, x=x)
# 係数coefは最初の要素が定数項，線形効果，非線形効果の順に格納されている
lines(y=res_n$coef[1] +res_n$coef[-1], x=x[-1], col="black")
lines(y=res_i$coef[1] +res_i$coef[-1], x=x[-1], col="red")
lines(y=res_ci$coef[1]+res_ci$coef[-1], x=x[-1], col="blue")
legend("topleft", legend=c("N", "I", "CI"), lty=1, col=c("black", "red", "blue"))

推定結果は以下の通りになります．

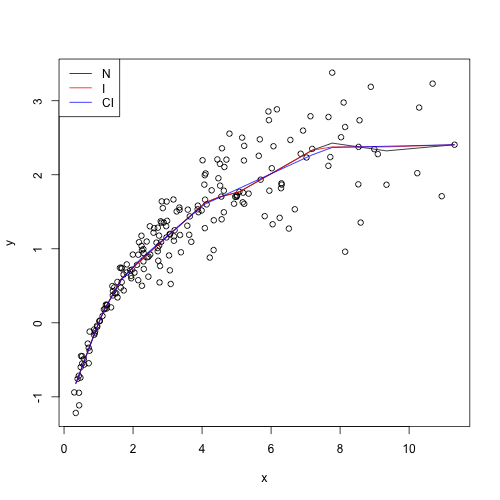
関数の形状が事前にわかっている場合には，より強い制約を課すことで若干ではありますがきれいに関数を推定することができます．

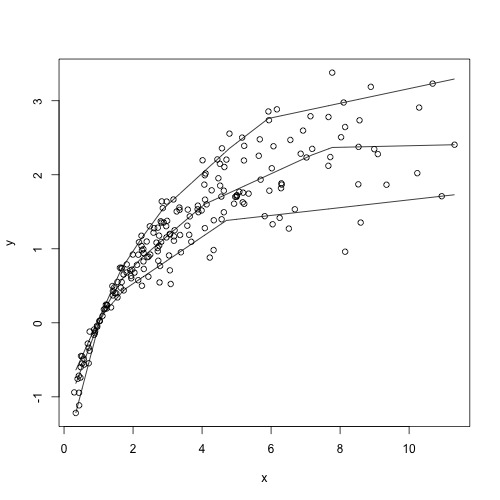
また単調増加凹の場合について$\tau=0.1, 0.5, 0.9$の場合についても推定してみます．ただしrqss関数は引数tauにベクトルを取れないのでループで各分位点について別個に推定します．

plot(y=y, x=x)
for (i in 1:length(tau)){
    res_ci <- rqss(y~qss(x, constraint="CI"), tau=tau[i])
    lines(y=res_ci$coef[1]+res_ci$coef[-1], x=x[-1])
}

最後に

今回は頻度論における分位点回帰モデルを取り上げました．分位点回帰モデル全般について学びたい方はKoenker (2005)やKoenker etal. (2017)を参考にしてみてください．一方でベイズ統計学においても分位点回帰モデルその拡張性の高さから大きな関心を集めてきました．次回はベイズ分位点回帰モデルについてはまた今後記事を書いていきたいと思います．

参考文献

Koenker, R. (2005). Quantile Regression. Cambridge University Press, Cambridge.
Koenker, R., Chernozhukov, V., He, X., Peng. L. (2017). Handbook of Quantile Regression. Chapman & Hall/CRC, Boca Raton.

株式会社Nospareでは分位点回帰モデルに限らず，統計学の様々な分野を専門とする研究者が所属しております．統計アドバイザリーやビジネスデータの分析につきましては弊社までお問い合わせください．