こんにちは,株式会社Nospareリサーチャー・千葉大学の小林です.前の記事「[R]分位点回帰をベイズ推定してみる」 ではベイズの枠組みにおける分位点回帰モデルを紹介しましたが,本記事では打ち切りデータに対するベイズ分位点回帰モデルを取り上げます.
打ち切りとは
まず被説明変数に打ち切り(ここでは例として右側)があるとはどういうことかについて説明します.ここで実際に観測される被説明変数$y_i$に対して観測されない潜在的な被説明変数$y_i^*$を次の式で結びつけます
y_i = \min\left\{y_i^*, c\right\}.
ここである閾値$c$について,潜在的な$y_i^*$が$c$を下回った場合には$y_i^*$の値がそのまま観測され,上回った場合には$c$が観測されるということを表しています.右側の打ち切りは,例えばなにかイベントが起こる(患者が死亡する,機械が壊れる)までの時間を$y_i^*$,(予算などの都合で)観測を終了する時刻を$c$とします.時刻$c$までにイベントが起きていればその時刻がそのまま観測されるのに対し,観測終了時においてイベントが起きていなければそれ以降の観測ができないので$c$とだけ観測されます(すくなくとも時刻$c$までは生存していた).左側打ち切りの場合には
y_i = \max\left\{y_i^*, c\right\}.
と表現します.経済学で労働者の労働時間についての分析を行う場合に$c=0$の左側打ち切りの考え方を用いたりします(Tobitモデル).労働から得られる効用が正の場合にはその効用の値が労働時間として観測され,負の場合には労働を選択しない,つまり観測される労働時間がゼロということです.
打ち切りのあるベイズ分位点回帰
通常の回帰部モデルと比べて分位点回帰の枠組みで打ち切りのある被説明変数を扱うのは統計学的推論的にも数値計算的に困難な課題でした.ところが非対称ラプラス分布に基づいたベイズ推定においてはこれが驚くほど簡単に適用することができます.まず分位点は単調変換に対して不変であるので,打ち切りがかかった被説明変数の分位点は,打ち切りがかかっていない分位点に打ち切りをかけたものと等しくなります.よって,潜在的な$y_i^*$について分位点回帰モデルを考えます:
y_i^* = x_i'\beta_\tau + \epsilon_i,
$\epsilon_i$は非対称ラプラス分布に従います.そして$y_i$と$y_i^*$を上の打ち切りのメカニズムによって結びつけます.
前回紹介した非対称ラプラス分布の混合表現を使って,回帰モデルはこのように書けます
y_i^*=x_i'\beta_\tau + v\theta_1 + \sqrt{\sigma v \theta_2^2}z
ここで$v\sim Exp(\sigma)$,$z\sim N(0,1)$,$\theta_1=(1-2\tau)/\tau(1-\tau)$,$\theta_2^2=2/\tau(1-\tau)$です.
MCMCによるベイズ推定において$y_i=c$と打ち切られたデータに対しては,データ拡大法によって完全条件付事後分布から$y_i^*$を発生させてあたかもすべてのデータが観測されたかのように他のパラメータのサンプリングを行っていきます.このように通常のベイズ分位点回帰モデルのMCMCに$y_i^*$をサンプリングするステップだけ加えるだけでいいということです.
頻度論では
頻度論では,左側打ち切りのデータに対する分位点回帰モデルの回帰係数は
\min_{\beta_\tau}\sum_{i=1}^n\rho(y_i-\max\{c,x_i'\beta_\tau\})
によって得られます.$\rho$はチェックロスです.被説名変数が打ち切られている場合の推測方法の構築や数値計算の安定性は挑戦的な研究テーマでした.今回は取り扱いませんが,Rでは以前紹介したquantregパッケージのcrq()関数でこのモデルを使った分析ができます.
再びBrqパッケージ
Brqパッケージではそんな打ち切りのある分位点回帰モデルを推定できます.ただし,左側に打ち切りのあるバージョン(Tobit分位点回帰)しか取り扱えません...Brq()関数においてmethod=Btqrとし,leftという上記の$c$に対応する左側打ち切りの閾値を指定するだけでいいです(デフォルトではゼロ).
# 先程と同じ設定でデータを生成する
set.seed(1)
n <- 200
x <- rnorm(n)
ys <- rnorm(n, mean=1+2.0*x)
# ysを0で左側を打ち切る
y <- pmax(ys, 0)
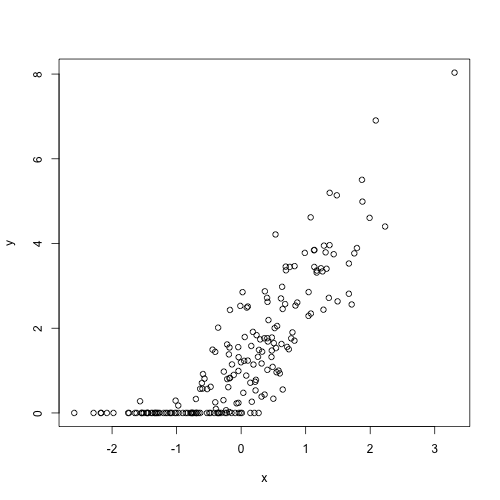
plot(y=y, x=x)
打ち切ったデータはこのようになります.
このデータに対してBrq()関数を使い,method="Btqr",left=0と指定します.
res <- Brq(y~x, tau=c(0.1,0.5,0.9), method="Btqr", left=0, runs=11000, burn=1000)
summary(res)
実行すると
$tau
[1] 0.1
$coefficients
Estimate L.CredIntv U.CredIntv
[1,] -0.2095131 -0.3897879 -0.0521164
[2,] 1.9587274 1.7546510 2.1779446
$tau
[1] 0.5
$coefficients
Estimate L.CredIntv U.CredIntv
[1,] 0.9102426 0.7449792 1.060319
[2,] 1.9402662 1.7507598 2.156534
$tau
[1] 0.9
$coefficients
Estimate L.CredIntv U.CredIntv
[1,] 2.10189 1.962641 2.256092
[2,] 1.91273 1.763909 2.097180
各分位点において$x$の係数パラメータの事後平均が真値である2に近く,また95%信用区間も真値を含んでいることからうまく機能していることがわかります.
ではこのデータに対して打ち切りを考慮しないで分析を行ったらどうなるでしょうか.
res <- Brq(y~x, tau=c(0.1,0.5,0.9), runs=11000, burn=1000)
summary(res)
結果は以下の通り,係数が正しく推定されないことがわかります.
$tau
[1] 0.1
$coefficients
Estimate L.CredIntv U.CredIntv
[1,] 0.3739603 0.2812704 0.4644157
[2,] 0.9288185 0.7439967 1.1228274
$tau
[1] 0.5
$coefficients
Estimate L.CredIntv U.CredIntv
[1,] 1.334646 1.206587 1.471720
[2,] 1.283826 1.108878 1.468776
$tau
[1] 0.9
$coefficients
Estimate L.CredIntv U.CredIntv
[1,] 2.538112 2.394296 2.679508
[2,] 1.333992 1.235872 1.445509
データ分析の問題を一緒に解決しませんか
被説名変数に打ち切りがある場合にもベイズ分位点回帰モデルは簡単に推定することができます.
打ち切りがあるデータに対して通常の分位点回帰モデルを当てはめると正しい分析結果が得られません.分析する際に手元にあるデータが打ち切られたものとして扱うかどうかは,データが観測される過程について考える必要があります.もしデータ分析でお困りのことがあれば株式会社Nospareまでお問い合わせください.ベイズ統計学に限らず統計学の様々な分野を専門とする研究者が所属しており,様々な問題を解決できます!