More than 3 years have passed since last update.

【ベイズ統計学】ロジットモデルに対するギブスサンプリングを簡単に行う！（R編）

Last updated at 2021-04-02Posted at 2021-04-02

こんにちは，株式会社Nospareリサーチャー・千葉大学の小林です．前回の記事では２項ロジットモデルなどロジスティック型の関数がモデルに含まれるときに，Polya-Gamma（PG）mixtureの表現方法を使うことでメトロポリスヘイスティングス（MH）アルゴリズムを使わずにPG分布からのデータ拡大法によって簡単なギブスサンプラーを適用することができる，ということについて説明しました．後編にあたる本記事では２項ロジットモデルと負の二項分布をベイズ推定するためのRでの実装について取り上げることにします．

２項ロジットモデル

被説明変数を$y_i$, $i=1,\dots,N$とします．$y_i$は$0$か$1$の値を取ります．例えば来店時にある製品カテゴリからの購入があった場合に$y_i=1$，なかった場合に$y_i=0$が観測されます．前回の記事でも述べたように，試験の合格・不合格，ある疾患の有無など２つの起こりうる結果のうちどちらかひとつが起こるという選択行動や出来事に関するデータの分析において非常によく用いられます．ロジットモデルでは$y_i=1$が起こる確率（ここでは選択確率と呼ぶことにします）を説明変数のベクトル$x_i$を用いて次のようにモデル化します．

\Pr(y_i=1)=\frac{\exp(x_i'\beta)}{1+\exp(x_i'\beta)},\quad i=1,\dots,N.

ここで$\beta$は$x_i$に対する係数パラメータです．

二項ロジットモデルの場合には，$w_i$の完全条件付分布は単純に$PG(1,x_i'\beta)$となります．よって$\beta\sim N(b_0,B_0)$の場合，次のふたつのステップから成るギブスサンプラーを実行します：

$i=1,\dots,N$まで，$w_i$を$PG(1,x_i'\beta)$からサンプリングする
$\beta$を$N(b_1,B_1)$からサンプリングする，ただし$B_1=\left[X'W X+ B_0^{-1}\right]^{-1}$, $b_1=B_1\left[X'W z+ B_0^{-1}b_0\right]$，$z_i=(y_i-0.5)/w_i$, $z=(z_1,\dots,z_N)'$，$W=diag(w_1,\dots,w_N)$．

以下がMCMCのコードになります．

library(BayesLogit)
library(mvtnorm)
library(mcmcse)

logistic <- function(x){
    ex <- exp(x)
    ex/(1+ex)
}


set.seed(1)
# サンプルサイズ
N  <- 500
# 説明変数の数
P  <- 3

# 真値
beta_true <- matrix(1,nrow=P)

# データを発生させる
X  <- cbind(1, matrix(rnorm(N*(P-1)), nrow=N, ncol=P-1))
pp <- logistic(X%*%beta_true)
Y  <- apply(pp, 1, rbinom, n=1, size=1)

# パラメータを初期化
par_beta <- matrix(0, nrow=P)
par_w    <- rep(1,N)
par_eta  <- X%*%par_beta

# 事前分布
prior_b0    <- matrix(0, nrow=P)
prior_B0    <- 100*diag(P)
prior_invB0 <- solve(prior_B0)

# mcmcの設定
burn <- 2000
draw <- 5000
thin <- 1

storage   <- draw / thin
ss        <- floor((draw+burn)/10)

# ストレージ 
result1 <- list(beta=array(0,dim=c(storage,P)))

# MCMC
cc <- 1
start_time <- proc.time()
for (it in 1:(draw+burn)) {
    # wのサンプリング
      par_w <- rpg(num=N, h=1, z=par_eta)
  
    # betaのサンプリング
    Z <- (Y - 0.5) / par_w
    B <- solve(t(X)%*%(X*par_w) + prior_invB0)
    b <- B %*% (t(X)%*%(Z*par_w) + prior_invB0%*%prior_b0)
    par_beta <- t(rmvnorm(1, mean=b, sigma=B))
    par_eta  <- X%*%par_beta
    par_pi   <- logistic(par_eta)

    # サンプルを保存
    if ( it > burn & (it%%thin)==0 ) {
        result1$beta[cc,]  <- par_beta
        cc <- cc + 1
    }   

    if(it%%ss==0){
        print(it)
    }

}
end_time <- proc.time()
comp_time1 <- (end_time-start_time)[3]

# essを計算
ess1 <- ess(result1$beta)

print(comp_time1)
print(ess1)
print(ess1/comp_time1)
print(summary(result1$beta))

# サンプルパス
png("fig1.png", height=300, width=900)
par(mfrow=c(1,P))
for (j in 1:P){
    plot(result1$beta[,j], type="l", ylab=bquote(beta[.(j)]), xlab="iteration", main=bquote(beta[.(j)]) )
    abline(h=beta_true[j], col="red")
}
dev.off()

# 自己相関関数
png("fig2.png", height=300, width=900)
par(mfrow=c(1,P))
for (j in 1:P){
    auto <-acf(result1$beta[,j], type="correlation", main=bquote(beta[.(j)]))
    
}
dev.off()

ここでは$N=500$， $p=3$，$X_{ij}\sim N(0,1),\ j=1,\dots,p$，パラメータの真値を$\beta=(1,1,1)'$，$\beta$の事前分布は$N(0,100)$としています．前述の通り，このギブスサンプラーではPG分布からのサンプリングが必要なので，BayesLogitパッケージのrpg()関数を使用します．

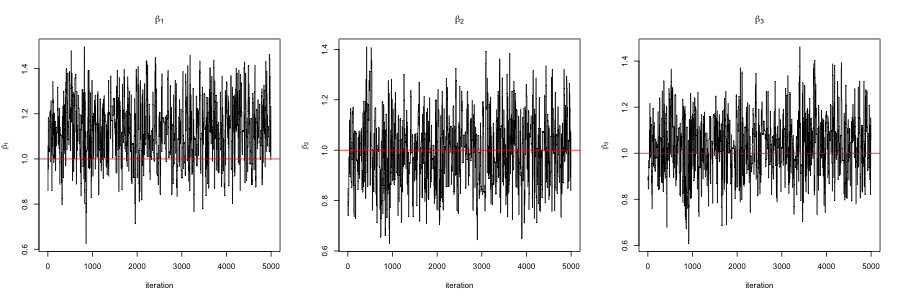
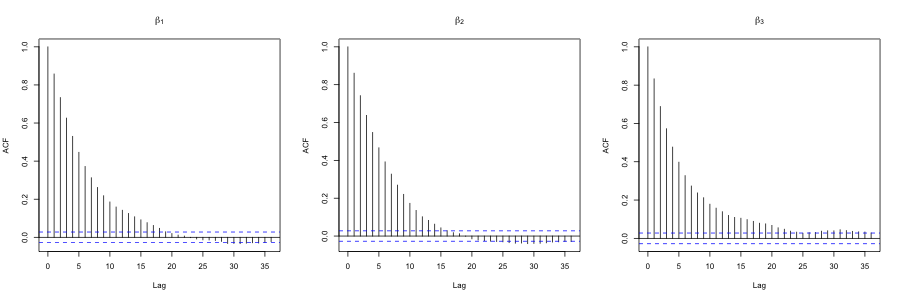
次の図はこのコードを実行して得られたMCMCのサンプルパス（赤線は真値を表します）と自己相関関数を表しています．

コードがうまく動作していることがわかります．また，MCMCのサンプルの自己相関も結構早く減衰しています．
比較のために$\beta$を正規分布のランダムウォークを使ったMHアルゴリズムでサンプリングした結果も以下に載せておきます．

ランダムウォークのステップサイズは採択率が0.24ほどになるように設定しました．こういったチューニングが必要であるのに加え，ギブスサンプラーに比べて自己相関関数の減衰が遅いことがわかります．

7000回（うちburn-in2000回）回すのにギブスサンプラーの計算時間は約2.9秒だったのに対し，MHは約0.5秒でした．
次の表はMCMCのサンプルの有効サンプルサイズ(ESS)と計算時間1秒あたりのESS（ESS/s，ESSを計算時間で割ったもの）をまとめています．

	ギブスのESS	MHのESS	ギブスのESS/s	MHのESS/s
$\beta_1$	1887	474	638	877
$\beta_2$	1958	440	666	813
$\beta_3$	1753	334	596	617

これを見てみるとESS自体は上の図のようにギブスサンプラーのほうがよい結果になって入るのですが，1秒あたりのESSはMHのほうがよい結果になりました．

負の二項分布

負の二項分布はポアソン分布の代替としてカウントデータの分析によく用いられます．ポアソン分布では平均と分散が等しいことが制約的ですが，負の二項分布は分散が平均よりも大きく，大きな観測値を許容します．応用先として，例えばある期間における入院患者数，感染症の感染者数，パッケージ製品の購入数など，カウントデータ分析において幅広く用いることができます．
負の二項分布の確率関数は

p(y_i)=\frac{\Gamma(\xi+y_i)}{\Gamma(\xi) y_i! } (1-\psi_i)^\xi\psi_i^{y_i},\quad  y_i=0,1,2,\ldots

と書け（$\xi>0$はoverdispersionのパラメータ），負の二項分布における回帰モデルは$\psi_i=e^{x_i'\beta}/(1+e^{x_i'\beta})$と与えられます．事前分布$\beta\sim N(b_0,B_0)$の場合，ギブスサンプラーは次のような形式になります．
　

$i=1,\dots,N$まで，$w_i$を$PG(y_i+\xi,x_i'\beta)$からサンプリングする．
$\beta$を$N(b_1,B_1)$からサンプリングする，ただし$B_1=\left[X'W X+ B_0^{-1}\right]^{-1}$, $b_1=B_1\left[X'W z+ B_0^{-1}b_0\right]$, $z=(z_1,\dots,z_N)'$, $z_i=\frac{y_i-\xi}{2w_i}$.
$\xi$をサンプリングする．

$\xi$のサンプリングはMHアルゴリズムでも大丈夫なのですが，チューニングフリーを目指すために以下にあげるコードでは$\xi\sim Ga(a,b)$という事前分布のもと，$\xi$のサンプリングをChinese restaurant table（CRT）分布を使った方法でギブスサンプリングしています．具体的には新たに$l_i$というCRT分布に従う変数を導入し，まず$l_i$をサンプリングしてその次に$\xi$をサンプリングします．$l_i$のサンプリングはベルヌーイ確率変数の和によって行います

l_i=\sum_{j=1}^{y_i}u_j，\quad u_j\sim Bernoulli\left(\frac{\xi}{\xi+j-1}\right),\quad i=1,\dots,N.

そして$\xi$をガンマ分布

Ga\left(a+\sum_{i=1}^Nl_i,b-\sum_{i=1}^N\log(1-\psi_i)\right)

からサンプリングします．

下のコードでは$N=2000$， $p=3$，$X_{ij}\sim N(0,1),\ j=1,\dots,p$，パラメータの真値を$\beta=(1,1,1)'$，$\beta$の事前分布は$N(0,100)$，$\xi$の事前分布は$Ga(0.1,0.1)$としています．

library(BayesLogit)
library(mvtnorm)
library(mcmcse)

logistic <- function(x){
    ex <- exp(x)
    ex/(1+ex)
}


set.seed(1)
# サンプルサイズ
N <- 2000
# 説明変数の数
P <- 3

# 真値
beta_true <- matrix(1,nrow=P)
xi_true   <- 10.0

# データを発生させる
X  <- cbind(1, matrix(rnorm(N*(P-1)), nrow=N, ncol=P-1))
sc <- X%*%beta_true
Y  <- matrix(0, nrow=N)
for (i in 1:N){
    tmp <- rgamma(1, shape=xi_true, scale=exp(sc[i]))
    Y[i] <- rpois(1, tmp)
}

# パラメータの初期化
par_beta <- matrix(0, nrow=P)
par_w    <- rep(1,N)
par_eta  <- X%*%par_beta
par_psi   <- logistic(par_eta)
par_xi   <- 1.0

# 事前分布
prior_b0 <- matrix(0, nrow=P)
prior_B0 <- 100*diag(P)
prior_invB0 <- solve(prior_B0)
prior_xi    <- c(0.1, 0.1)

# mcmcの設定
burn <- 2000
draw <- 5000
thin <- 1

storage   <- draw / thin
ss        <- floor((draw+burn)/10)

# ストレージ
result1 <- list(beta=array(0,dim=c(storage,P)), xi=rep(0,storage))

# CRTからサンプリング
rcrtnb <- function(s, xi){
    if(s>0){
        pr <- c(1, xi/(xi+(2:s)-1))
        return(sum(rbinom(s, size=1, prob=pr)))
    } else{
        return(0)
    }
}
    
# mcmc
cc <- 1
start_time <- proc.time()
for (it in 1:(draw+burn)) {
    # xiのサンプリング
    l  <- apply(Y, 1, rcrtnb, xi=par_xi)
    a1 <- prior_xi[1] + sum(l)
    b1 <- prior_xi[2] - sum(log(1.0-par_psi))
    par_xi <- rgamma(1, shape=a1, rate=b1)

    # wのサンプリング
    par_w <- rpg(num=N, h=par_xi+Y, z=par_eta)

    # betaのサンプリング
    Z <- 0.5*(Y-par_xi) / par_w
    B <- solve(t(X)%*%(X*par_w) + prior_invB0)
    b <- B %*% (t(X)%*%(Z*par_w) + prior_invB0%*%prior_b0)
    par_beta <- t(rmvnorm(1, mean=b, sigma=B))
    par_eta  <- X%*%par_beta
    par_psi  <- logistic(par_eta)

    ## サンプルを保存
    if ( it > burn & (it%%thin)==0 ) {
        result1$beta[cc,]  <- par_beta
        result1$xi[cc]     <- par_xi
        cc <- cc + 1
    }   

    if(it%%ss==0){
        print(it)
    }

}
end_time <- proc.time()

comp_time1 <- (end_time-start_time)[3]

# essを計算
ess1 <- ess(cbind(result1$beta,result1$xi))

print(comp_time1)
print(round(ess1,1))
print(round(ess1/comp_time1,1))
print(summary(result1$beta))
print(summary(result1$xi))

# サンプルパス
png("fig5.png", height=300, width=1200)
par(mfrow=c(1,P+1))
for (j in 1:P){
    plot(result1$beta[,j], type="l", ylab=bquote(beta[.(j)]), xlab="iteration", main=bquote(beta[.(j)]) )
    abline(h=beta_true[j], col="red")
}
plot(result1$xi, type="l", ylab=expression(xi), main=expression(xi))
abline(h=xi_true, col="red")
dev.off()

# 自己相関関数
png("fig6.png", height=300, width=1200)
par(mfrow=c(1,P+1))
for (j in 1:P){
    auto <-acf(result1$beta[,j], type="correlation", lag.max=100, main=bquote(beta[.(j)]))
}
auto <-acf(result1$xi, type="correlation", main=expression(xi), lag.max=100)
dev.off()

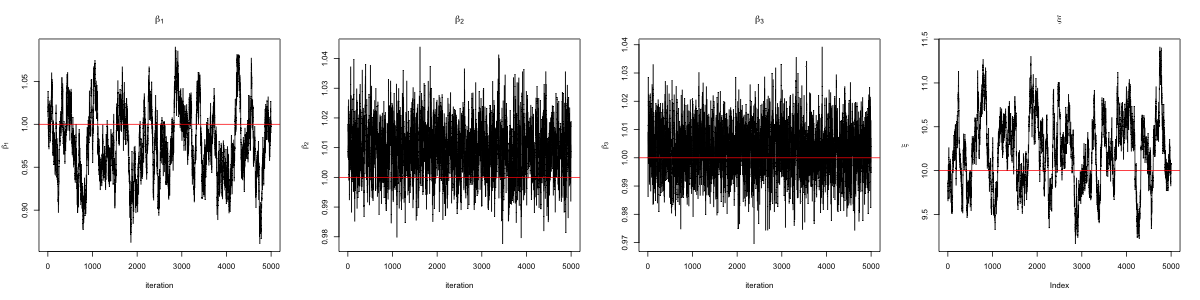
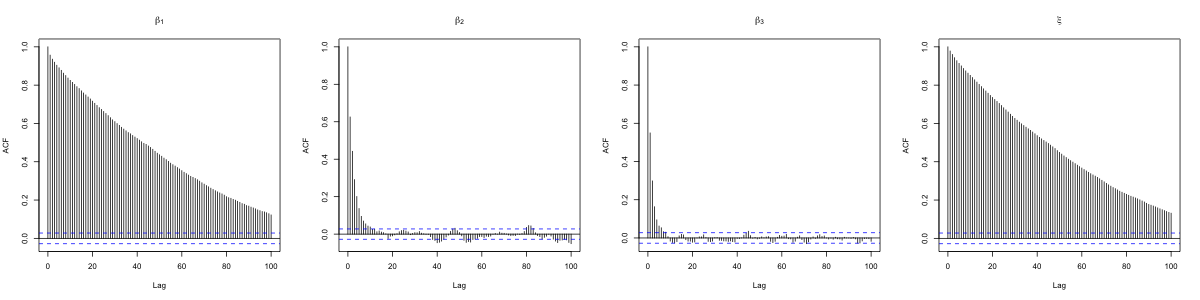
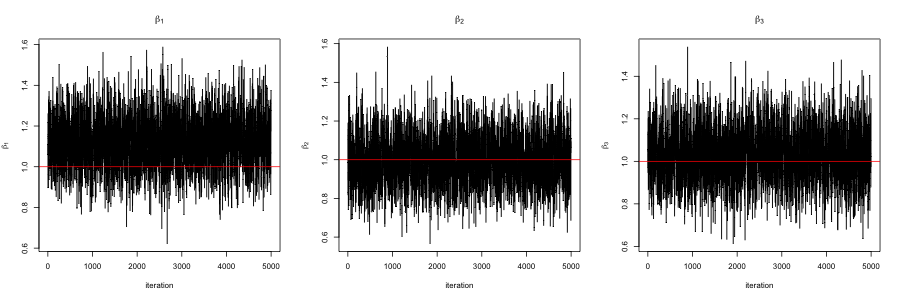
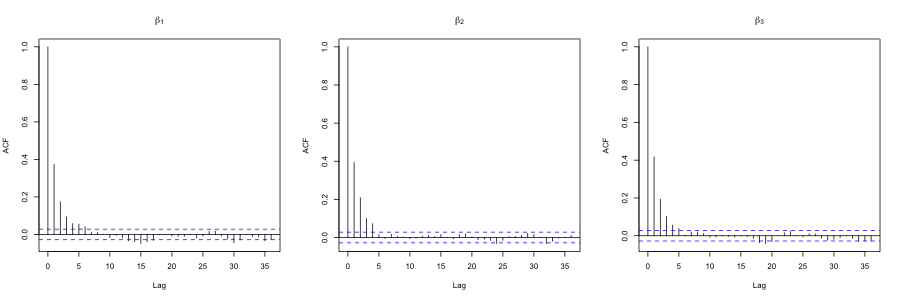
次の図はこのコードを実行して得られたMCMCのサンプルパスと自己相関関数を表しています．
基本的に問題なく作動しているように見えますが，$\beta_1$と$\xi$の依存性が高く，これらのパラメータの自己相関が比較的高い結果となっています．

次に正規分布のランダムウォークのMHアルゴリズムの結果と比較してみます．このMHアルゴリズムでは$\beta$と$\xi$をひとつのブロックで更新し，ここでも採択率がおよそ0.24になるようにランダムウォークのステップサイズをチューニングしています．ギブスサンプラーと同様に$\beta_1$と$\xi$の自己相関が高い結果となっていますが，ギブスサンプラーよりも自己相関の減衰が遅いことが見て取れます．

次の表では上記の$\xi$をCRTでサンプリングするギブスサンプラー（PG+CRT，約189秒），$\xi$をランダムウォークMHでサンプリングするギブスサンプラー（PG+RW，約92秒），ランダムウォークMH（約6秒）のESSと1秒あたりのESSをまとめています．ESS単体で見るとPG+CRTが一番よい結果になっていますが，計算時間1秒あたりのESSでは計算時間の短いMHアルゴリズムがよい結果になっています．

	PG+CRT のESS	PG+RW のESS	MHのESS	PG+CRT のESS/s	PG+RW のESS/s	MHのESS/s
$\beta_1$	62.4	34.5	12.1	0.3	0.4	2.0
$\beta_2$	995.6	880.1	298.5	5.2	10.1	48.9
$\beta_3$	1238.8	1009.1	202.5	6.5	13.0	33.2
$\xi$	42.6	33.7	11.4	0.2	0.3	1.9

#おわりに
本記事では二項ロジットモデルと負の二項分布をPolya-Gammaの定式化に基づいてベイズ推定するためのRコードを紹介しました．RではBayesLogitパッケージやpgdrawパッケージを使うことでスクラッチでコードを書かなくてもPG分布からのサンプリングを行うことができます．ここで紹介した2つの単純なモデルにおいてはMHアルゴリズムが計算時間あたりの効率性が一番よい，というちょっと期待はずれな結果になりました．一方で，この定式化に基づいたギブスサンプラーの利点はやはりチューニングが不要になるということで，階層モデルなどもっと複雑なモデルにおいてよりアドバンテージを発揮することが考えられます．ちなみに，ここで紹介した２つのコードを組み合わせてあともうひと手間加えるとこの論文で取り上げられているZero-inflated negative binomial（ゼロ超過のある負の二項分布）モデルのベイズ推定もギブスサンプラーだけで行うことができます．

一緒にお仕事しませんか！
株式会社Nospareではベイズ統計学に限らず統計学の様々な分野を専門とする研究者が所属しており，新たな知見を日々追求しています．統計アドバイザリーやビジネスデータの分析につきましては弊社までお問い合わせください．

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up