ゼロから作るDeep LearningをJuliaで実装してみる (2)活性化関数 #DeepLearning

この記事の目的

本記事は、Deep Learningの入門書「ゼロから作るDeep Learning」を参考に、Juliaを用いて同書の内容を実装してみる、という試みです。

※これはあくまで筆者の一つの試みと提案で、必ずしも内容が正解ではありませんのでご了承お願い致します。
また、より良いアドバイスや協力のご提案などありましたら、お気軽にお声がけ頂けますと幸いです。

今回取り組むこと

本記事は、参考書の3.2章にあたります。
以下の3つの活性化関数を実装してみます。
　①ステップ関数
　②シグモイド関数
　③ReLU関数

①ステップ関数

入力パラメータが一つの整数または実数の場合のステップ関数は以下のように実装できます。

2_activatioin_function

function step_function(x)
    if x > 0.0
        return 1
    else
        return 0
    end
end

参考書に合わせ、入力パラメータが一次元配列の場合のステップ関数を考えます。
map関数を使用し、配列の各要素が0.0より大きいか小さいかを判定します。
判定結果をfloat型に変換して返す関数を作成します。

2_activatioin_function

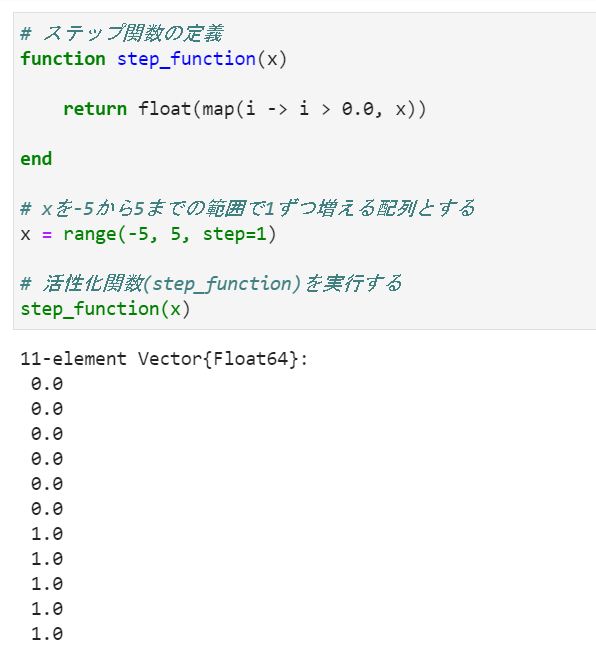
function step_function(x)
    return float(map(i -> i > 0.0, x))
end

実際の動作確認の結果は以下の通りです。

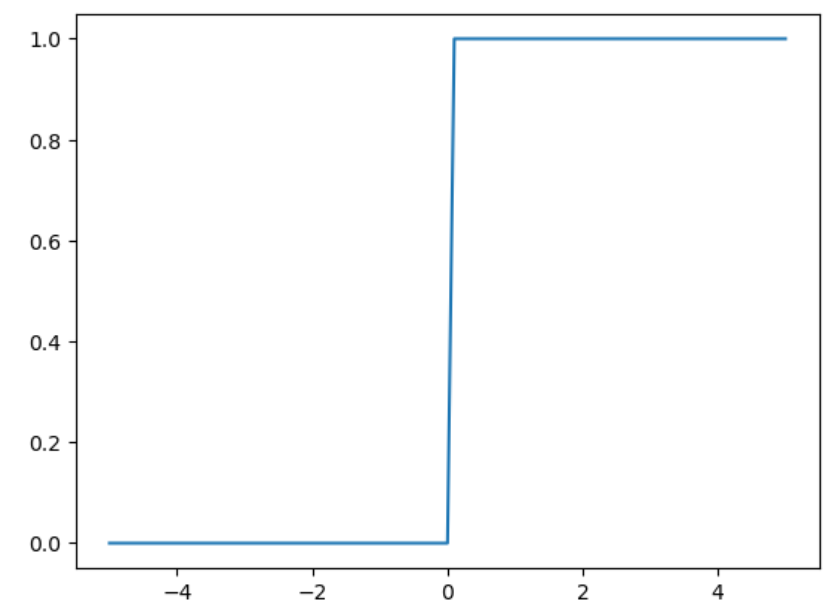
上記のステップ関数をグラフに表してみます。
グラフはPythonと同じMatplotlibによりグラフ描画を実行します。

※Matplotlibによるグラフ描画では、予めPythonのインストール及びMatplotlibのインストールが必要です。
インストール方法についてはこちらをご参照下さい。

Julia早引きノート［23］JuliaでのMatplotlibによるグラフ描画
https://qiita.com/ttabata/items/96a0e172addfac690cca

予め以下のようにインポートの宣言をしておきます。
using PyPlot

以下のようにプログラムを作成しました。

2_activatioin_function

using PyPlot


# ステップ関数の定義
function step_function(x)
    return float(map(i -> i > 0.0, x))
end

# xを-5から5までの範囲で0.1ずつ増える配列とする
x = range(-5, 5, step=0.1)

# ステップ関数を実行し、yに格納します。
y = []
y = step_function(x)

# グラフ描画(x-y座標上にプロット)
plot(x, y)

グラフ描画の実行結果です。

②シグモイド関数

シグモイド関数(sigmoid function)は一般的に以下のように定義されます。
eをネイピア数とします。

\frac{1}{1+e^{-x}}\quad(式1)

入力パラメータが一つの整数または実数の場合のシグモイド関数を以下のように実装してみます。

2_activatioin_function

function sigmoid_function(x)
    return 1 / (1 + exp(-x))
end

次に、ステップ関数の場合と同様に入力パラメータが一次元配列の場合のシグモイド関数を考えます。
map関数を使用し各要素に対して(式1)を計算し、結果を返すという形式にします。

2_activatioin_function

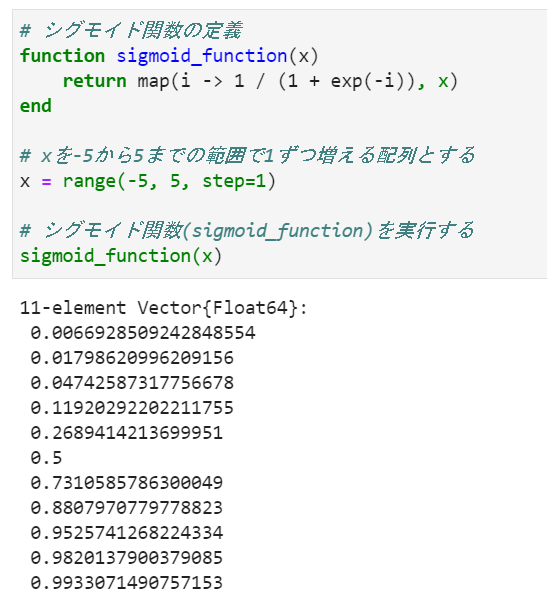
function sigmoid_function(x)
    return map(i -> 1 / (1 + exp(-i)), x)
end

実際の動作確認の結果は以下の通りです。

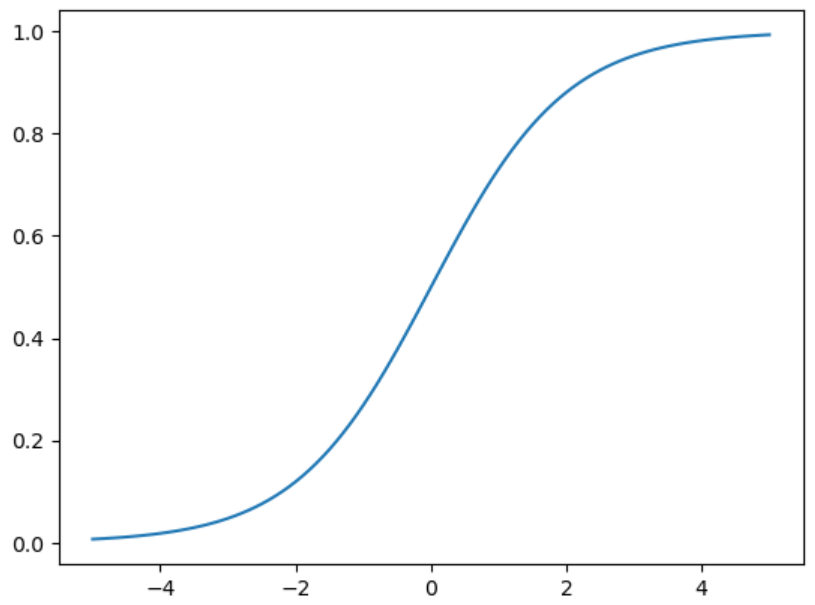
上記のシグモイド関数をグラフに表してみます。
以下のようにプログラムを作成しました。

2_activatioin_function

using PyPlot

# シグモイド関数の定義
function sigmoid_function(x)
    return map(i -> 1 / (1 + exp(-i)), x)
end

# xを-5から5までの範囲で0.1ずつ増える配列とする
x = range(-5, 5, step=0.1)

# シグモイド関数を実行し、yに格納します。
y = []
y = sigmoid_function(x)

# グラフ描画(x-y座標上にプロット)
plot(x, y)

グラフ描画の実行結果です。

③ReLU関数

ReLU関数は以下のように定義されます。

f(x) = \left\{
\begin{array}{ll}
x & (x \gt 0) \\
0 & (x \le 0)
\end{array}
\right.
\quad(式2)

入力パラメータが一つの整数または実数の場合のReLU関数を以下のように実装してみます。

2_activatioin_function

function relu_function(x)
    return max(0, x)
end

シグモイド関数と同様に、入力パラメータが一次元配列の場合のReLU関数を考えます。
map関数を使用し各要素に対して(式2)を計算し、結果を返すという形式にします。

2_activatioin_function

function relu_function(x)
    return map(i -> max(0, i), x)
end

実際の動作確認の結果は以下の通りです。

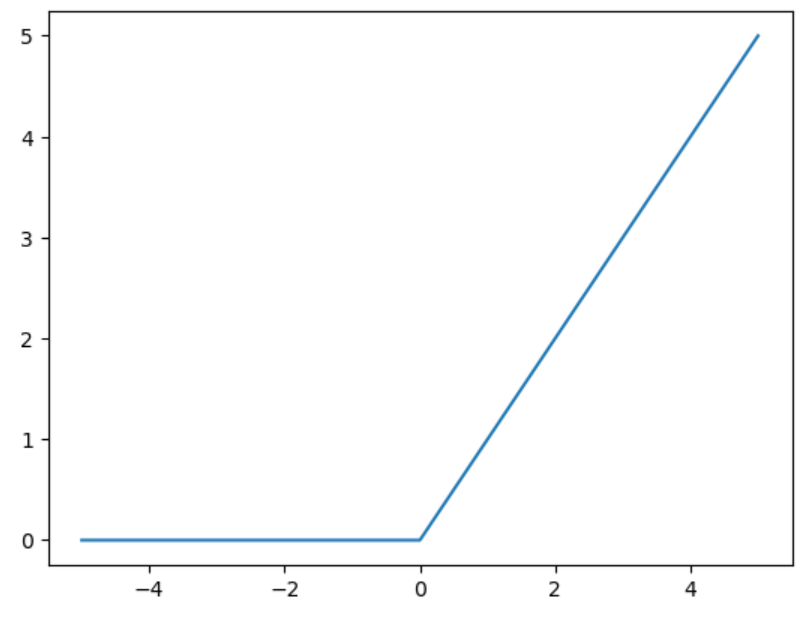
上記のReLU関数をグラフに表してみます。
以下のようにプログラムを作成しました。

2_activatioin_function

using PyPlot

# ReLU関数の定義
function relu_function(x)
    return map(i -> max(0, i), x)
end

# xを-5から5までの範囲で0.1ずつ増える配列とする
x = range(-5, 5, step=0.1)

# シグモイド関数を実行し、yに格納します。
y = []
y = relu_function(x)

# グラフ描画(x-y座標上にプロット)
plot(x, y)

グラフ描画の実行結果です。

以上で活性化関数の実装ができました。
次回は多次元配列の計算を行います。

出典

■参考書
「ゼロから作るDeep Learning ～ Pythonで学ぶディープラーニングの理論と実装」
　斎藤康毅著／オライリー・ジャパン

ご意見など

ご意見、間違い訂正などございましたらお寄せ下さい。

ゼロから作るDeep LearningをJuliaで実装してみる (2)活性化関数

この記事の目的

今回取り組むこと

①ステップ関数

②シグモイド関数

③ReLU関数

もくじ

関連情報

出典

ご意見など