適宜修正や追記を行いながら、勉強した内容を共有していきたいと思います。
※現状、主に回帰タスクにフォーカスして書いています。
他のタスクにおいては、仕様が異なる箇所があるかもしれませんので留意ください。
(ざっと確認している範囲では、タスク間で概ね仕様は共通な様です。)
本ドキュメントについて
PyCaretの前処理にフォーカスしています。
基本的に、モデリングやチューニングなどの部分には触れておりません。
実際に動かしつつ、本家ソースコードを読んだりもしながら記述しております。
https://github.com/pycaret/pycaret
※誤ってる箇所もあるかもしれませんが、あらかじめご了承ください。
実装上の前提
次のように各種ライブラリはimportしているものとします。
import pandas as pd
import numpy as np
PyCaretとは
データの前処理および機械学習モデルのトレーニングを自動化し、ローコード環境でデプロイ可能なライブラリです。
https://pycaret.org/
なお、インストールはpipコマンド一発です。とても簡単。。
pip install pycaret
概要やパイプラインの一連の実装方法については、こちらの記事が参考になります。
https://qiita.com/tani_AI_Academy/items/62151d7e151024733919
前処理の実行方法
PyCaretでは、実行したい前処理をパラメータで指定することができます。
また、PyCaretは動作前に一部の処理内容について、ユーザーへの確認を行います。
動作フローは次のようなイメージです。

データ入力/前処理の実行関数を呼び出す
classificationやregressionといったタスクごとに用意されたパッケージがもつsetup()を呼出すことで、下記のような前処理が実行されます。
- データクリーニングやデータ変換
- train/testのデータ分割
- データサンプリング
PyCaretに処理させたい前処理は、setup()へ引数として与えることで指定可能です。
引数としては、「target(目標変数)」のみが必須となります。
以降の説明では、PyCaretに付属しているデータを取得して実行していきたいと思います。
PyCaret付属のデータについては、本家ページで確認することが出来ます。
https://pycaret.org/get-data/
※もちろん、自前のデータをpandasで読み込んで使うことも可能です。
データ取得、および前処理を実行するコードは下記の通りです。
ここでは、引数「target」のみを指定しています。他のオプションはデフォルト値となります。
from pycaret.datasets import get_data
dataset = get_data("diamond")
from pycaret.regression import *
setup(dataset, target="Price")
※なお、ここではreturn値をスルーしていますが、前処理後のデータなど複数の値が返されます。
return値については、後述の「setup()のreturn値」を確認ください。
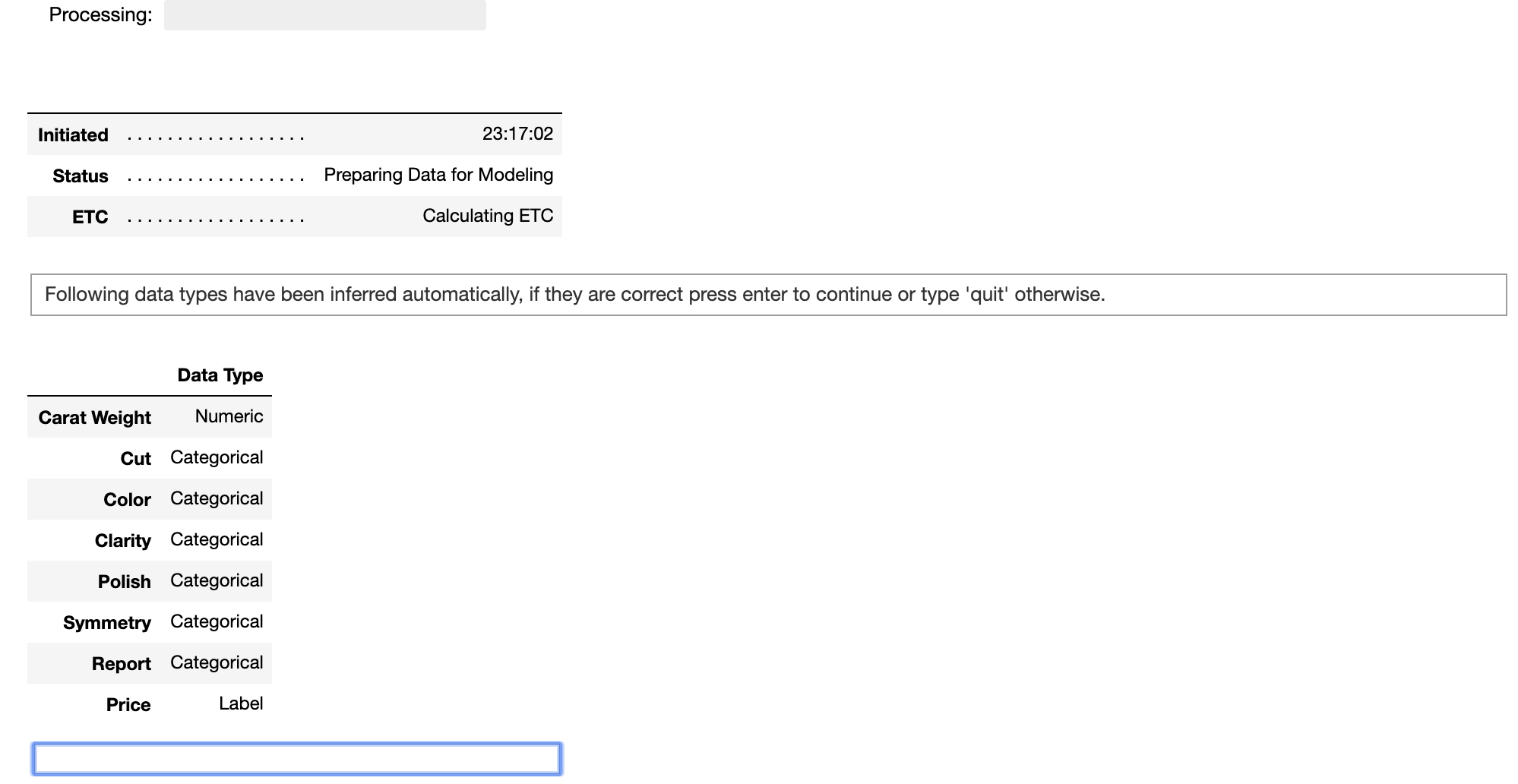
各変数の型の推定結果を確認する
setup()を実行すると、PyCaretは、まず各変数の型(Data Type)を推定して、ユーザに推定結果の確認と処理の続行を促します。
型の推定結果が正しければ、図の青枠のエディットボックスにEnterキーを入力することで処理を続行します。
推定された型がおかしな場合は、「quit」と入力することで処理を中断できます。
型の推定が誤っている変数については、setup()へ明示的に型を指定してやることで解消します。
(詳細は、後述の「Numeric Features および Categorical Features」を確認ください。)
また、setup()の引数として「silent=True」を渡すことで、型推定の確認をスキップして、処理を続行することができます。
前処理の実行サマリを確認する
setup()の実行が終わると、処理内容がデータフレーム形式で出力されます。
| Description | Value | |
|---|---|---|
| 0 | session_id | 3104 |
| 1 | Transform Target | False |
| 2 | Transform Target Method | None |
| 3 | Original Data | (6000, 8) |
| 4 | Missing Values | False |
| 5 | Numeric Features | 1 |
| 6 | Categorical Features | 6 |
| 7 | Ordinal Features | False |
| 8 | High Cardinality Features | False |
| 9 | High Cardinality Method | None |
| 10 | Sampled Data | (6000, 8) |
| 11 | Transformed Train Set | (4199, 28) |
| 12 | Transformed Test Set | (1801, 28) |
| 13 | Numeric Imputer | mean |
| 14 | Categorical Imputer | constant |
| 15 | Normalize | False |
| 16 | Normalize Method | None |
| 17 | Transformation | False |
| 18 | Transformation Method | None |
| 19 | PCA | False |
| 20 | PCA Method | None |
| 21 | PCA Components | None |
| 22 | Ignore Low Variance | False |
| 23 | Combine Rare Levels | False |
| 24 | Rare Level Threshold | None |
| 25 | Numeric Binning | False |
| 26 | Remove Outliers | False |
| 27 | Outliers Threshold | None |
| 28 | Remove Multicollinearity | False |
| 29 | Multicollinearity Threshold | None |
| 30 | Clustering | False |
| 31 | Clustering Iteration | None |
| 32 | Polynomial Features | False |
| 33 | Polynomial Degree | None |
| 34 | Trignometry Features | False |
| 35 | Polynomial Threshold | None |
| 36 | Group Features | False |
| 37 | Feature Selection | False |
| 38 | Features Selection Threshold | None |
| 39 | Feature Interaction | False |
| 40 | Feature Ratio | False |
| 41 | Interaction Threshold | None |
この表から、データサイズや特徴量の数や、各種前処理の指定の有無などを確認ができます。
デフォルトでは、ほとんどのオプションが無効(FalseやNone)です。
setup()の引数でオプションを指定すると、該当項目が「True」となり色塗りされます。

次節以降で、各種項目についての内容を解説していきます。
セッションに関する情報
session_id
| Description | Value | |
|---|---|---|
| 0 | session_id | 3104 |
PyCaretの実行時の識別子で、内部的には乱数のseedとして使っている模様です。
指定しないとランダムに決定されます。
setup()の引数「session_id」で指定が可能です。
繰り返し実行時に、再現性を保つ場合にこちらの値を指定します。
(scikit-learnにおける「random_state」に近いイメージですね。)
setup(dataset, target="Price", session_id=123)
入力データに関する情報
Original Data
| Description | Value | |
|---|---|---|
| 3 | Original Data | (6000, 8) |
| 入力データのサイズ(shape)が出力されます。 |
実際に確認してみると、たしかに同じサイズです。
dataset.shape
# 実行結果
# (6000, 8)
Missing Values
| Description | Value | |
|---|---|---|
| 4 | Missing Values | False |
| 入力データの欠損の有無が出力されます。 | ||
| 今回のデータには欠損が含まれていないため「False」が出力されています。 |
なお、欠損がある場合、setup()の中で欠損埋めが処理されます。
欠損埋めの手法の指定については後述します。
Numeric Features および Categorical Features
| Description | Value | |
|---|---|---|
| 5 | Numeric Features | 1 |
| 6 | Categorical Features | 6 |
| それぞれ、連続値およびカテゴリの特徴量の個数の推測値が出力されます。 |
setup()の引数「numeric_features」および「categorical_features」で明示的に指定できます。
setup(dataset, target="Price",
categorical_features=["Cut", "Color", "Clarity", "Polish", "Symmetry", "Report"],
numeric_features=["Carat Weight"])
上述したPyCaretによる型推定の確認ダイアログにおいて、型推定が誤っている変数がある場合、本引数で明示的に指定してやります。
train / testのデータ分割に関する情報
Transformed Train Set、Transformed Test Set
| Description | Value | |
|---|---|---|
| 11 | Transformed Train Set | (4199, 28) |
| 12 | Transformed Test Set | (1801, 28) |
| train / testデータに分割後のそれぞれのサイズが出力されます。 | ||
train / testデータの分割の割合は、setup()の引数「train_size」で指定が可能です。 |
||
| デフォルトは0.7です。 |
なお、カラム数は前処理後の特徴量数が表示されているため、入力データとは異なります。
(今回は、前処理により特徴量の数が7から28に増えています。)
データサンプリングに関する情報
Sampled Data
| Description | Value | |
|---|---|---|
| 10 | Sampled Data | (6000, 8) |
| ``setup()`内でデータのサンプリングを行った場合に、サンプル後のデータ数が出力されます。 | ||
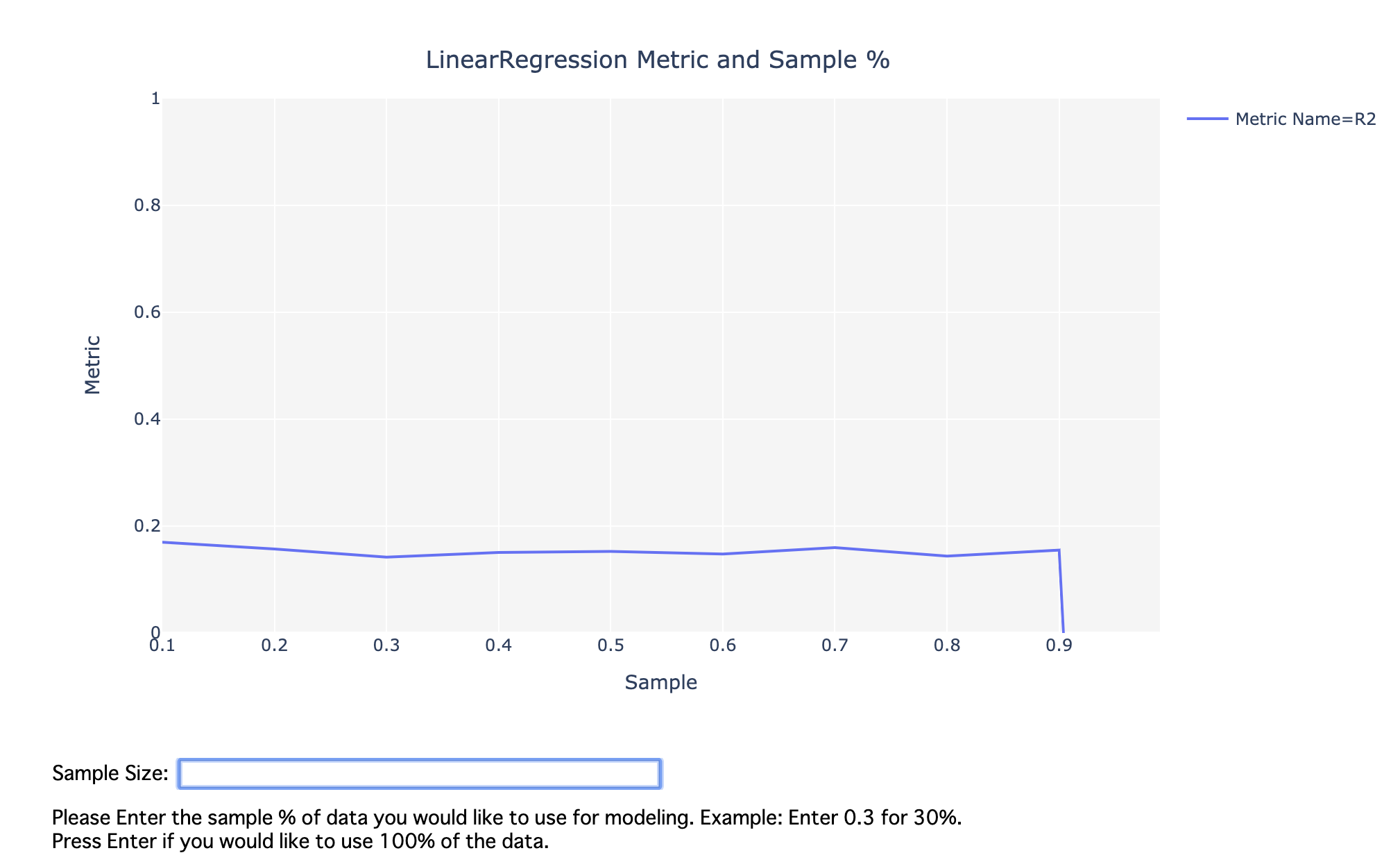
| PyCaretは、データ行数が25,000よりも大きい場合に、データをサンプリングした上で一連の処理を実行することを促します。 |
行数が25,000を超えるデータでsetup()を実行すると、型推定の確認ダイアログ実行後に、サンプリングの実行確認ダイアログが表示されます。
サンプリングを行う場合は、青枠のエディットボックスにサンプリングするデータの割合を入力します。
サンプリングせず全行数を使用する場合は空欄のままEnterキーを入力します。
ここで描画されるグラフは、サンプリングによる精度の劣化の目安を示したものとなります。
- 回帰タスクにおいては、(デフォルトでは線形回帰モデルの)決定係数をプロットしたもの
- 分類タスクにおいては、(デフォルトではロジスティック回帰モデル)の各種指標をプロットしたもの
このプロットに使用するモデルは、setup()の引数「sample_estimator」で指定することができます。
例えば、RandomForestRegressorを指定するコードは下記の通りです。
from sklearn.ensemble import RandomForestRegressor
traffic = get_data("traffic")
setup(traffic, target="traffic_volume", sample_estimator=RandomForestRegressor())
また、setup()の引数「sampling」を指定することで、この機能自体をOFFすることができます。
(サンプリングの実行有無の確認は行われず、全てのデータを使用して処理を継続します。)
(その他)データクリーニング・特徴量の変換処理に関する手法
その他の項目については、データクリーニングや特徴量の変換処理の実行有無や手法に関する情報です。
次章にて、それぞれに該当する処理を解説していきます。
データクリーニングおよび特徴量の変換処理
処理内容および指定方法を考察していきます。
setup()のreturn値
setup()を呼び出すと、前処理後のデータや処理パイプラインが返ってきます。
なお、解きたいタスクの種類によって異なるようです。
X, y, X_train, X_test, y_train, y_test, seed, prep_pipe, target_inverse_transformer, experiment__ \
= setup(dataset, target="Price")
from pycaret.classification import *
dataset = get_data('credit')
X, y, X_train, X_test, y_train, y_test, seed, prep_pipe, experiment__ \
= setup(dataset, target = 'default')
regressionとclassificationでは、微妙にreturn値が異なります。
Xやyには前処理後のデータが返ってくるため、具体的な処理結果を確認することができます。
PyCaretによる前処理後のデータに対して、さらに自前で加工を行い、PyCaretへ設定し直せるのか?については、現状分かっていません。
※引き続き調査していきたいと思います。
特徴量の除外
前処理や以降のモデリングで除外する特徴量を設定できます。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- ignore_features(stringのリスト型, default = None)
- 除外したい特徴量のカラム名をリストで指定します。
参考
IDと日付(datetime)は、デフォルトでモデリング時に除外する設定となっている様です。
なお、日付のカラムが日付として認識されない場合、「date_features」という引数で明示的に指定できる様です。
また、正しい仕様は確認中ですが、全く同じデータのカラムがある場合にも片方を自動で除外するような挙動をします。
欠損埋め
欠損を、指定した方法で補間します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- numeric_imputation(string型, default = 'mean')
- 数値データに対する欠損埋めの方法を指定します。
- 'mean'または'median'を指定可能です。
- 'mean'は平均値で欠損を埋めます。
- 'median'は中央値で欠損を埋ます。
- 'mean'または'median'を指定可能です。
- 数値データに対する欠損埋めの方法を指定します。
- categorical_imputation(string型, default = 'constant')
- カテゴリデータに対する欠損埋めの方法を指定します。
- 'constant'または'mode'を指定可能です。
- 'constant'は、常に「not_available」という文字列で埋めます。
- 'mode'は、特徴量ごとの最頻値で埋めます。
- 'constant'または'mode'を指定可能です。
- カテゴリデータに対する欠損埋めの方法を指定します。
参考
現時点ではカラムごとに指定はできず、全て統一の手法で処理する様です。
順序データのエンコード
順序データとして定義したいカラムを指定することで、ラベル変換します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- ordinal_features(dictionary型, default = None)
- 順序データのカラム名と値の順序を辞書形式で指定します。
以下のようなイメージで指定します。
ordinal_features = { 'column_name' : ['low', 'medium', 'high'] }
辞書データのvalue部分には、順序データの小さい方から順に値を指定します。
特徴量の正規化
各特徴量を正規化します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- normalize(bool型, default = False)
- 本処理の実行有無(True/False)を指定します。
- normalize_method(string型, default = 'zscore')
- 正規化に使用するメソッド(下記のいずれか)を定義します。
- 'zscore' : 標準化と呼ばれる手法で、z = (x - u) / s として計算します。
- 'minmax' : Min-Maxスケーリングと呼ばれる手法で、0-1の範囲にスケーリングします。
- 'maxabs' : 最大、最小の絶対値を1にスケーリングします。
- `robust' : データの四分位点を基準にしてスケーリングします。
- 正規化に使用するメソッド(下記のいずれか)を定義します。
参考
'robust'スケーリングについては、こちらの記事が参考になります。
https://qiita.com/unhurried/items/7a79d2f3574fb1d0cc27
データセットに外れ値が含まれている場合、'robust'スケーリングが強いようです。
その他のスケーリングについては、こちらの記事が参考になります。
https://qiita.com/Umaremin/items/fbbbc6df11f78532932d
一般的に、線形アルゴリズムでは、正規化した方が精度がよくなる傾向がありますが、必ずしもそうなるとは限らないため複数の実験が必要になるかと思います。
カテゴリ変数内のレア値の統合
カテゴリ変数において、指定した閾値未満となるカテゴリを1つのカテゴリとして統合します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- combine_rare_levels(bool型, default = False)
- 本処理の実行有無(True/False)を指定します。
- rare_level_threshold(float型, default = 0.1)
- レア値とみなすしきい値を指定します。
- 出現頻度がしきい値未満となるカテゴリを、全て1つのカテゴリとして統合します。
- しきい値未満となるカテゴリが2つ以上存在するときのみ有効となります。
- 統合されたカテゴリは「XXX_others_infrequent」というような名称で定義されます。
参考
一般的にこの手法は、カテゴリ変数に大量のカテゴリがある場合にダミー変数化することで疎行列となるようなケースを回避します。
数値データのビン化
数値データの特徴量をビン化します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- bin_numeric_features(stringのリスト型, default = None)
- ビン化したい数値データ特徴量のカラム名をリストで指定します。
参考
内部的には、sklearn.preprocessing.KBinsDiscretizerを実行するイメージです。
(1次元のk-means法を用いたアルゴリズムを用いる模様です。)
※ビン数の決め方などの詳細は理解していないので、今後勉強していきたいと思います。
外れ値の除去
trainデータから外れ値を除去します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- remove_outliers(bool型, default= False)
- 本処理の実行有無(True/False)を指定します。
- outliers_threshold(float型, default= 0.05)
- データセット内の外れ値の割合を指定します。
- たとえばデフォルトの0.05を指定すると、分布の裾の両側の値の0.025%が除去されます。
- データセット内の外れ値の割合を指定します。
参考
内部的な処理には、特異値分解やPCAを用いている模様です。
※詳細は理解していないので、今後勉強していきたいと思います。
マルチコの除去
マルチコ(多重共線性)が発生しうる特徴量を除去します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- remove_multicollinearity(bool型, default= False)
- 本処理の実行有無(True/False)を指定します。
- multicollinearity_threshold(float型, default= 0.9)
- 本パラメータで定義されたしきい値よりも高い相互相関を持つ変数が削除されます。
- (2つの特徴量のうち、目的変数との相関が低い方を削除する様です。)
- 本パラメータで定義されたしきい値よりも高い相互相関を持つ変数が削除されます。
参考
マルチコについては、こちらの記事が参考になります。
https://qiita.com/ynakayama/items/36b7c1640e6a02ce2e00
クラスリング結果の特徴量化
各特徴量を用いたクラスタリングを行い、各レコードのクラスラベルを新たな特徴量として追加します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- create_clusters(bool型, default=False)
- 本処理の実行有無(True/False)を指定します。
- cluster_iter(int型、default=20)
- クラスタ数を決める際の反復数を指定します。
参考
クラスターの数は、Calinski Harabasz基準とシルエット基準の組み合わせを使用して決定される模様です。
Calinski Harabasz基準とシルエット基準については、こちらの記事が参考になります。
https://qiita.com/yasaigirai/items/ec3c3aaaab5bc9b930a2
データの分散による特徴量の除去
統計的に有意ではない分散を持つ特徴量を削除します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- ignore_low_variance(bool型, default=False)
- 本処理の実行有無(True/False)を指定します。
参考
ここでいうデータの分散は、全サンプルのうちの一意の値(unique値)の比率などを使用して計算される様です。
ある変数において「同じ値」が多いほど分散が低いとみなし、除外の候補となるイメージでしょうか。
※詳細は理解していないので、今後勉強していきたいと思います。
交互作用特徴量の生成
指定したパラメータを用いて、交互作用特徴量を生成します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- polynomial_features(bool型, default = False)
- Trueを指定すると、全ての数値データ特徴量の多項式の組み合わせで新たな特徴量を生成します。
- 多項式の次数は、polynomial_degree paramで指定します。
- ただし、生成される特徴量のうち、重要でないと判断したものは除外されます。
- polynomial_thresholdで判定のしきい値を設定します。
- trigonometry_features(bool型, default = False)
- Trueを指定すると、全ての数値データ特徴量の三角関数の組み合わせで新たな特徴量を生成します。
- 次数やしきい値は、polynomial_features同様に指定します。
- polynomial_degree(int型, default = 2)
- 多項式特徴の次数を指定します。
- polynomial_threshold(float型、default = 0.1)
- 新たに生成した特徴量を残すか否かを判定するしきい値を指定します。
- (判定方法については下記の「参考」を参照ください。)
- 新たに生成した特徴量を残すか否かを判定するしきい値を指定します。
たとえば、入力が[a、b]2つの変数の場合、polynomial_degree=2を指定すると、[1, a, b, a^2, ab, b^2]という特徴量が生成されるイメージです。
上記に加えて、さらに交互作用特徴量を指定できます。
カテゴリ変数のダミー変数特徴量や、polynomial_features、trigonometry_featuresにより生成した特徴も含むすべての数値データ特徴量に対して、1次の交互作用特徴量を生成します。
- feature_interaction(bool型、default = False)
- Trueを指定すると、交互作用(a * b)を計算し、新しい特徴量として生成します。
- ただし、生成される特徴量のうち、重要でないと判断したものは除外されます。
- polynomial_thresholdで判定のしきい値を設定します。
- feature_ratio(bool型、default = False)
- Trueを指定すると、比率(a / b)を計算し、新しい特徴量として生成します。
- しきい値は、feature_interaction同様に指定します。
- interaction_threshold(bool型、default = 0.01)
- 新たに生成した特徴量を残すか否かを判定するしきい値を指定します。
- (判定方法については下記の「参考」を参照ください。)
- 新たに生成した特徴量を残すか否かを判定するしきい値を指定します。
参考
polynomial_thresholdおよびinteraction_thresholdについて
しきい値と比較する指標は、ランダムフォレスト、AdaBoost、および線形相関など複数の組み合わせに基づく重要度の様です。
※詳細は理解していないので、今後勉強していきたいと思います。
trigonometry_featuresについて、こちらは文字とおり三角関数(sin, cos, tan)を用いた特徴量を作る?のでしょうか。
※詳細は理解していないので、今後勉強していきたいと思います。
本機能は、大きな特徴量空間を持つデータセットでは非効率となる可能性があるので注意が必要です。
グループ特徴量の生成
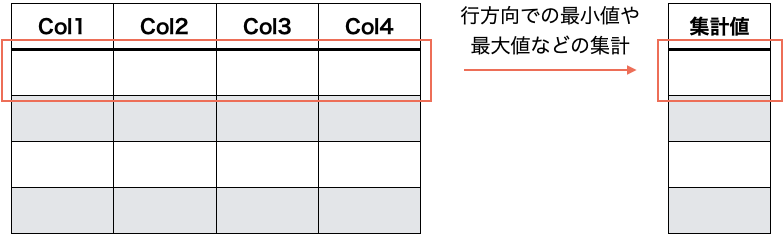
データセット内に、関連し合う特徴量を指定することで、それらを基にした統計的な特徴量を抽出します。
指定する特徴量間の下記のような集計値を計算し新たな特徴量を生成します。
- 最小値
- 最大値
- 平均値
- 中央値
- 最頻値
- 標準偏差
パラメータ
setup()へ下記の引数を与えることで実行できます。
- group_features(stringのlist型 または listを包含したlist型, default = None)
- グループ特徴量を生成したい(関連する)数値データ特徴量のカラム名を指定します。
- group_names(list型, default = None)
- 各グループ名を文字列で指定できます。
- 「グループ名_Min」というイメージで集計値ごとにカラム名が付けられます。
- group_featuresと長さが一致しないか、本引数が指定されない場合、group_1、group_2という順番で名前が付けられます。
- 各グループ名を文字列で指定できます。
実装イメージは下記の通りです。
setup(dataset, target="Price", group_features=[["cal1", "cal2" "cal3"], ["cal4", "cal5"]], group_names=["gr1", "gr2"])
特徴量選択の実行
いくつかの評価指標を用いて特徴量を選択します。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- feature_selection(bool型, default = False)
- 本処理の実行有無(True/False)を指定します。
- feature_selection_threshold(float型、デフォルト= 0.8)
- 特徴選択に使用される割合しきい値を指定します。(新しく生成される多項式特徴量なども含みます)
- この値が大きいほど、選択される特徴量の数が多くなります。
- 特徴選択に使用される割合しきい値を指定します。(新しく生成される多項式特徴量なども含みます)
参考
feature_selection_thresholdについて
しきい値と比較する指標は、ランダムフォレスト、AdaBoost、および線形相関など複数の組み合わせに基づく重要度の様です。
※詳細は理解していないので、今後勉強していきたいと思います。
本家ソースコメントによれば、polynomial_featuresおよびfeature_interactionを使用する場合は、本パラメータは低い値で定義したほうが良いとのことです。
交互作用で作成した特徴量は、本処理である程度絞っておいた方が良いというイメージでしょうか。
高カーディナリティ特徴量の低減
高いカーディナリティを持つカラムを指定することで、カラム内のデータ種類を削減し、カーディナリティを低くします。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- high_cardinality_features(string型, default = None)
- 変換する(高カーディナリティ)カラムを指定します。
- high_cardinality_method(string型, default = 'frequency')
- 変換方法を指定します。
- 'frequency'または'clustering'が選択可能です。
- 'frequency'を指定すると、データ種別ごとの出現頻度(数値)で元のデータを置き換えます。
- 'clustering'を指定すると、クラスタリングを実行し、その結果(クラスラベル)で元データを置き換えます。
参考
※カーディナリティデータについてはこちらの記事が参考になります。
https://qiita.com/soyanchu/items/034be19a2e3cb87b2efb
'clustering'による手法では、本家のソースをざっと眺めた感じではk-meansを用いてそうです。
※カーディナリティの低減による効用等については理解しきれていないので、今後勉強していきたいと思います。
特徴量のスケーリング
指定した方法により特徴量をスケーリングします。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- transformation(bool型, default = False)
- 本処理の実行有無(True/False)を指定します。
- transformation_method(string型, default = 'yeo-johnson')
- 変換方法を指定します。
- 'yeo-johnson'または'quantile'が選択可能です。
- 'yeo-johnson'は、Yeo-Johnson変換を行います。
- 'quantile'は、 四分位変換?を行います。
参考
'yeo-johnson'および'quantile'どちらも、データを正規分布に従うように変換する様です。
※詳細は理解していないので、今後勉強していきたいと思います。
ざっと本家コードを確認したところ、'yeo-johnson'は、sklearn.preprocessing.PowerTransformer、'quantile'は、sklearn.preprocessing.QuantileTransformerを用いています。
一般的には、特徴量を正規分布に近づけることでモデリング時に有効になることがあります。
本家ソースコメントによると、'quantile'は非線形であり、同じ尺度で測定された変数間の線形相関を歪める可能性に注意が必要とのことです。
目的変数のスケーリング
指定した方法により目的変数をスケーリングします。
※現時点では、本項目はclassficationパッケージでは指定できません。
正規分布に近づけるための変換にのみ対応しており、それらは分類タスクにおいては不要な処理だからかと思われます。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- transform_target(bool型, default = False)
- 本処理の実行有無(True/False)を指定します。
- transform_target_method(string型, default = 'box-cox')
- 変換方法を指定します。
- 'Box-cox'または'yeo-johnson'が選択可能です。
- `Box-cox'は、Box-Cox変換を行います。
- 'yeo-johnson'は、Yeo-Johnson変換を行います。
参考
目的変数を正規分布に近づけることでモデリング時に有効になることがあります。
Box-Cox変換では全てのデータが正の値であるという制約があるため、データに負の値が含まれる場合は、強制的にYeo-Johnson変換に切り替える様です。
※Box-Cox変換についてはこちらの記事が参考になります。
https://qiita.com/dyamaguc/items/b468ae66f9ce6ee89724
特徴量の次元削減
特徴量の次元削減を行います。
パラメータ
setup()へ下記の引数を与えることで実行できます。
- pca(bool型, default = False)
- 本処理の実行有無(True/False)を指定します。
- pca_method(string型, default = 'linear')
- 'linear' : 主成分分析(線形)による次元削減を行います。
- 'kernel' : カーネル主成分分析による次元削減を行います。
- 'incremental' : 主成分分析(大量データver)による次元削減を行います。
- pca_components(int/float型, default = 0.99)
- 次元削減後に残す特徴量の数/割合を指定します。
- int型で指定すると、残す特徴量の数として扱われます。
- もともとの特徴量数よりも小さい値を指定する必要があります。
- float型で指定すると、残す特徴量の割合として扱われます。
- int型で指定すると、残す特徴量の数として扱われます。
- 次元削減後に残す特徴量の数/割合を指定します。
参考
一般的に、重要でない特徴量を削る、およびメモリ・CPU資源の節約を目的として実施します。
本処理(次元削減)は、前処理パイプラインの最後に実行する様です。
(他の前処理が完了した後のデータを対象に次元削減をします。)
主成分析についてはこちらの記事が参考になります。
https://qiita.com/shuva/items/9625bc326e2998f1fa27
https://qiita.com/NoriakiOshita/items/460247bb57c22973a5f0
'incremental'については、Incremental PCAという手法を用いる様です。
scikit-learnの解説によると、対象とするデータセットが大きすぎてメモリに収まらない場合に、主成分分析(PCA)の代わりに、Incremental PCA(IPCA)を用いると良いそうです。IPCAでは、入力データ数に依存しないメモリ量を用いて、入力データの低次元の近似を作成するとのことです。
https://scikit-learn.org/stable/auto_examples/decomposition/plot_incremental_pca.html
実装サンプル
特徴量を大量に作る
from pycaret.regression import *
X, y, X_train, X_test, y_train, y_test, seed, prep_pipe, target_inverse_transformer, experiment__ \
= setup(dataset, target="Price", session_id=123,
bin_numeric_features = ["Carat Weight"],
create_clusters = True,
polynomial_features = True, feature_interaction = True, feature_ratio = True)
setup()から出力される実行内容(抜粋)は下図の通りです。

returnされた前処理後のデータを確認すると、下記のように72の特徴量が生成されました。
print(X.info())
# 出力結果
# <class 'pandas.core.frame.DataFrame'>
# Int64Index: 6000 entries, 0 to 5999
# Data columns (total 72 columns):
# # Column Non-Null Count Dtype
# --- ------ -------------- -----
# 0 Carat Weight_Power2 6000 non-null float64
# 1 Cut_Fair 6000 non-null float64
# 2 Cut_Good 6000 non-null float64
# 3 Cut_Ideal 6000 non-null float64
# 4 Cut_Signature-Ideal 6000 non-null float64
# 5 Cut_Very Good 6000 non-null float64
# 6 Color_D 6000 non-null float64
# 7 Color_E 6000 non-null float64
# 8 Color_F 6000 non-null float64
# 9 Color_G 6000 non-null float64
# 10 Color_H 6000 non-null float64
# 11 Color_I 6000 non-null float64
# 12 Clarity_FL 6000 non-null float64
# 13 Clarity_IF 6000 non-null float64
# 14 Clarity_SI1 6000 non-null float64
# 15 Clarity_VS1 6000 non-null float64
# 16 Clarity_VS2 6000 non-null float64
# 17 Clarity_VVS1 6000 non-null float64
# 18 Clarity_VVS2 6000 non-null float64
# 19 Polish_EX 6000 non-null float64
# 20 Polish_G 6000 non-null float64
# 21 Polish_ID 6000 non-null float64
# 22 Polish_VG 6000 non-null float64
# 23 Symmetry_EX 6000 non-null float64
# 24 Symmetry_G 6000 non-null float64
# 25 Symmetry_ID 6000 non-null float64
# 26 Symmetry_VG 6000 non-null float64
# 27 Report_GIA 6000 non-null float64
# 28 Carat Weight_0.0 6000 non-null float64
# 29 Carat Weight_1.0 6000 non-null float64
# 30 Carat Weight_10.0 6000 non-null float64
# 31 Carat Weight_11.0 6000 non-null float64
# 32 Carat Weight_12.0 6000 non-null float64
# 33 Carat Weight_13.0 6000 non-null float64
# 34 Carat Weight_2.0 6000 non-null float64
# 35 Carat Weight_3.0 6000 non-null float64
# 36 Carat Weight_4.0 6000 non-null float64
# 37 Carat Weight_5.0 6000 non-null float64
# 38 Carat Weight_6.0 6000 non-null float64
# 39 Carat Weight_7.0 6000 non-null float64
# 40 Carat Weight_8.0 6000 non-null float64
# 41 Carat Weight_9.0 6000 non-null float64
# 42 data_cluster_0 6000 non-null float64
# 43 Polish_EX_multiply_Carat Weight_Power2 6000 non-null float64
# 44 Symmetry_EX_multiply_Carat Weight_Power2 6000 non-null float64
# 45 Report_GIA_multiply_Carat Weight_Power2 6000 non-null float64
# 46 Clarity_VVS2_multiply_Carat Weight_Power2 6000 non-null float64
# 47 Clarity_IF_multiply_Carat Weight_Power2 6000 non-null float64
# 48 Clarity_SI1_multiply_Carat Weight_Power2 6000 non-null float64
# 49 Carat Weight_Power2_multiply_data_cluster_0 6000 non-null float64
# 50 Symmetry_EX_multiply_data_cluster_0 6000 non-null float64
# 51 Report_GIA_multiply_data_cluster_0 6000 non-null float64
# 52 Symmetry_VG_multiply_Carat Weight_Power2 6000 non-null float64
# 53 Carat Weight_8.0_multiply_Carat Weight_Power2 6000 non-null float64
# 54 Cut_Signature-Ideal_multiply_Carat Weight_Power2 6000 non-null float64
# 55 data_cluster_0_multiply_Symmetry_EX 6000 non-null float64
# 56 Color_E_multiply_Carat Weight_Power2 6000 non-null float64
# 57 data_cluster_0_multiply_Cut_Ideal 6000 non-null float64
# 58 Carat Weight_Power2_multiply_Polish_EX 6000 non-null float64
# 59 data_cluster_0_multiply_Report_GIA 6000 non-null float64
# 60 Color_F_multiply_Carat Weight_Power2 6000 non-null float64
# 61 Carat Weight_Power2_multiply_Carat Weight_8.0 6000 non-null float64
# 62 Cut_Ideal_multiply_Carat Weight_Power2 6000 non-null float64
# 63 Color_D_multiply_Carat Weight_Power2 6000 non-null float64
# 64 data_cluster_0_multiply_Carat Weight_Power2 6000 non-null float64
# 65 data_cluster_0_multiply_Polish_EX 6000 non-null float64
# 66 Color_I_multiply_Carat Weight_Power2 6000 non-null float64
# 67 Polish_EX_multiply_data_cluster_0 6000 non-null float64
# 68 Color_H_multiply_Carat Weight_Power2 6000 non-null float64
# 69 Carat Weight_Power2_multiply_Report_GIA 6000 non-null float64
# 70 Clarity_VS2_multiply_Carat Weight_Power2 6000 non-null float64
# 71 Carat Weight_Power2_multiply_Symmetry_VG 6000 non-null float64
# dtypes: float64(72)
# memory usage: 3.3 MB
returnされた前処理のパイプラインを確認すると下記の通りです。
print(prep_pipe)
# 実行結果
# Pipeline(memory=None,
# steps=[('dtypes',
# DataTypes_Auto_infer(categorical_features=[],
# display_types=True, features_todrop=[],
# ml_usecase='regression',
# numerical_features=[], target='Price',
# time_features=[])),
# ('imputer',
# Simple_Imputer(categorical_strategy='not_available',
# numeric_strategy='mean',
# target_variable=None)),
# ('new_levels1',
# New_Catagorical_Levels_i...
# ('dummy', Dummify(target='Price')),
# ('fix_perfect', Remove_100(target='Price')),
# ('clean_names', Clean_Colum_Names()),
# ('feature_select', Empty()), ('fix_multi', Empty()),
# ('dfs',
# DFS_Classic(interactions=['multiply', 'divide'],
# ml_usecase='regression', random_state=123,
# subclass='binary', target='Price',
# top_features_to_pick_percentage=None)),
# ('pca', Empty())],
# verbose=False)
まとめ
PyCaretは様々なデータクリーニングや特徴量の変換処理を簡潔なコードで実現できる
PyCaretは、パラメータの指定のみで様々な前処理を記述でき、大幅な時間短縮に繋がると感じました。また、コードがすっきりし統一的な記述となるため、チーム内や自分自身にとっての読みやすさや思考の効率も向上するように思いました。
PyCaretでできる前処理を理解していくことは様々なテクニックの勉強にも繋がる
PyCaretは、コーディングが苦手な方にも比較的易しい作りです。これまでコーディングで躓いていた初学者の方にとっても、実際に動かしながら、理論の習得に注力できる良いツールになるのではないかと思いました。
(僕自身、今回調査を進める中で、今まで知らなかったテクニックを多く学ぶことができました。)
一方で (現時点では)PyCaretはあくまで効率化のためのツールである
PyCaretは、あくまでユーザから入力されたデータに基づき、クリーニングや特徴量の変換処理を行うものであり、仮説立てやデータ収集、特徴量設計についてはやはり人の手で行う必要があるという点を実感できました。