PCA
Kernel PCAの説明に入る前にPCAとは何か、ざっとおさらいしたいと思います。
PCAとは?
PCA(Principle Component Analysis)/主成分分析は、機械学習で主にデータの次元を減らすのに使われるテクニックです。「次元の呪い」としても知られるよう、特徴量が多すぎると学習に支障をきたします。なので、「不必要な特徴量はなるべく取り除きたい。本当に必要な特徴量だけを使いたい」のです。
PCAのメカニズム
各$x_i$がD次元(D個の特徴量)ベクトルのデータセットがあるとします。これをM次元に写すのに、y = Ax となる $A = [u_1^{T}, ... u_M^{T}]$、$u_k^{T}u_k = 1, k = 1,2... M$ があるとします。この時、PCAでは$y_i$の分散が最大になるAをみつけます。
A^* = argmax tr(S_y)
S_y=\dfrac {1}{N}\sum ^{N}_{i=1}\left( y_{i}-\overline {y}\right) \left( y_{i}-\overline {y}\right) ^{T}
\overline {y} = \dfrac {1}{N}\sum ^{N}_{i=1}x_i
$S_x$をSの分散共分散行列とした時、$tr(S_y) = tr(AS_xA^T)$により、ラグランジ定数を使い微分すると、下のような固有値ベクトル $u_k$による式になります。
S_xu_k = \lambda_ku_k
このように、PCAではxの分散が最大になるような固有値をとることで、特徴量を絞り出すことができます。
この固有値ベクトルによる写像は、下のような回転写像になります。
縦と横の広がりである、それぞれの特徴量の分散だけが残ったことがわかります。

Kernel PCA
上記のPCAでは、線形分離できるデータに対して次元削除を行いましたが、データが線形分離できない時に Kernel PCAを使います。
D次元の特徴量をもつデータをM次元に写す$\phi (x)$があるとします。この時、スタンダードなPCAを新たな次元空間で行うこともできますが、大変なので、カーネルトリックを使います。
まず、写像後の特徴量は平均0をとると仮定します。
\dfrac {1}{N}\sum ^{N}_{i=1} \phi(x_i) = 0
この時、分散共分散は
C = \dfrac {1}{N}\sum ^{N}_{i=1} \phi(x_i)\phi(x_i)^T
となります。
固有値ベクトル$v_i$は、下の式から求めることができます。
Cv_k = \lambda_k v_k
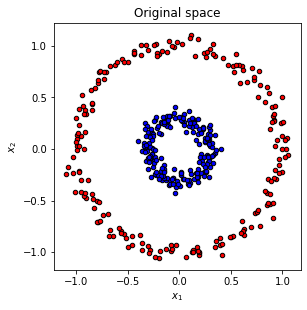
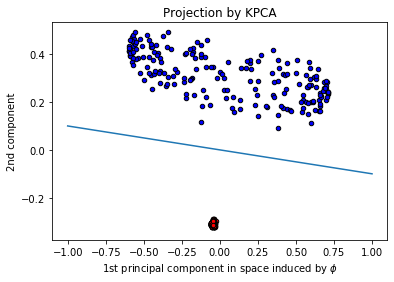
例えば、下のように、左のデータでは線形分離できませんが、カーネルを使うことで、線形分離可能になります。

scikit learn Kernel PCA
| パラメター | 概要 | 選択肢 | デフォルト |
|---|---|---|---|
| n_components | ターゲットの次元数 | int | None(そのまま) |
| kernel | カーネルタイプ | “linear” ,“poly” , “rbf” ,“sigmoid” ,“cosine” | "linear" |
| gamma | rbfとpolyのカーネル係数 | float | 1/n_features |
| degree | polyの係数 | int | 3 |
| coef0 | polyとsigmoidの独立係数 | float | 1 |
| kernel_params | カーネルのパラメターの名前 | Stringからのmapping | None |
| alpha | リッジ回帰 | 1.0 | |
| eigen_solver | 固有値の選択 | "auto", "dense", "arpack" | "auto" |
| tol | arpackの収束 | float | 0 |
| max_iter | arpackの最大反復回数 | int | None |
| remove_zeros | 固有値0の削除 | bool | False |
| random_state | arpackでのrandom_state | RandomState Instance or None | None |
| n_jobs | 並列作業 | int/None | None |
使用例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles
np.random.seed(0)
X, y = make_circles(n_samples=400, factor=.3, noise=.05)
plt.figure(figsize=(10,10))
plt.subplot(2, 2, 1, aspect='equal')
plt.title("Original space")
reds = y == 0
blues = y == 1
plt.scatter(X[reds, 0], X[reds, 1], c="red",s=20, edgecolor='k')
plt.scatter(X[blues, 0], X[blues, 1], c="blue",s=20, edgecolor='k')
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
-> 線形分裂できない。。。
RBFカーネル!
kpca = KernelPCA(kernel="rbf", fit_inverse_transform=True, gamma=10)
X_kpca = kpca.fit_transform(X)
pca = PCA()
X_pca = pca.fit_transform(X)
plt.scatter(X_kpca[reds, 0], X_kpca[reds, 1], c="red",s=20, edgecolor="k")
plt.scatter(X_kpca[blues, 0], X_kpca[blues, 1], c="blue",s=20, edgecolor="k")
x = np.linspace(-1, 1, 1000)
plt.plot(x, -0.1*x, linestyle="solid")
plt.title("Projection by KPCA")
plt.xlabel(r"1st PC induced by $\phi$")
plt.ylabel("2nd component")
分割後:
PCAの利点と欠点
利点
- 特徴量間の関係を無視できる。
- 学習がシンプルで速くなる。
- 過学習を防ぐ。
- より理解しやすい可視化。
欠点
- 元々の特徴量の解釈が難しくなる。
- 正規化が必要。
引用
Quan Wang, "Kernel Principal Component Analysis and its Applications in Face Recognition and Active Shape Models", 2014
https://arxiv.org/pdf/1207.3538.pdf