概要
背景
最近機会学習を始め、特徴量エンジニアリングを勉強している。
そのとき、Box-Cox変換を知ったのだか、この変換が何なのか、何をしているのか理解できなかったので、自分なりにできるだけ理解しやすいようにまとめてみた。
本投稿では、Box-Cox変換が何なのか、どう変換されるのかについて扱う。
Box-Cox変換を行うために必要な、ライブラリのインストールなど環境準備は記載しないので、他の記事を参照いただきたい。
環境
実行環境は次の通り。
$sw_vers
ProductName: Mac OS X
ProductVersion: 10.13.6
BuildVersion: 17G6030
$python3 --version
Python 3.7.3
Box-Cox変換とは
定義
Wikipedia( https://en.m.wikipedia.org/wiki/Power_transform )によるとBox-Cox変換は下のように定義される。
y^{(\lambda)} = \left\{
\begin{array}{ll}
\frac{x^{\lambda} - 1}{\lambda} & ( \lambda \neq 0)\\
\ln(x) & (\lambda = 0 )
\end{array}
\right.
ここで、$x$は変換したい変数、λは変換のパラメータで、λの値によって変換の関数形が異なる。
変換関数の概要
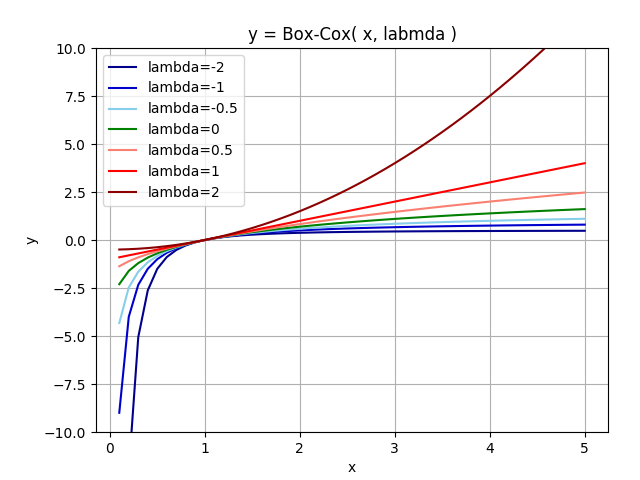
数式のままだと元の変数$x$がどう変換されるのか分かりにくいため、λの値を
[-2.0、-1.0、-0.5、0、0.5、1.0、2.0]のそれぞれに設定したときの関数をグラフに表した(下図)。
ここで分かる通り、$λ \leq 0$ のとき、$x \rightarrow 0$ とすると変換後の値$y$が$ - \infty $となってしまう。
また、$x$が負の値の場合には対応していない。
この問題に対応したものが、Yeo-Johnson変換だが、本投稿では記載しない。
$x > 0$ に着目すると、λの値によっていくつか特徴がある。
例えば、$λ < 0$のとき、$x \gg 1$では$y \rightarrow const$となる。
一方で、$λ > 0$のとき、$x \gg 1$では$y \rightarrow \infty$となる。
スケール変換の特徴をまとめると、下表のようになる。
| パラメータ | $x$:小 | $x$:大 |
|---|---|---|
| $\lambda < 0$ | $+$ | $-$ / (const) |
| $\lambda = 0$ | $+$ | $-$ |
| $0 < \lambda < 1$ | $+$ | $-$ |
| $\lambda > 1$ | $-$ | $+$ |
| ここで、$+$は変換によって$x$のスケールが伸びること、$-$は$x$のスケールが縮むことを表している。 |
したがって、例えばある分布に対してBox-Cox変換を施すと横軸の値$x$が小さい領域のスケールを縮めて、$x$が大きい領域のスケールを伸ばすというような変化をすることが分かる。
もちろん、λの値によって、その逆もあり得る。
Box-Cox変換の関数を描画したときに使ったコードは次の通り。
df_trans = pd.DataFrame({'x':np.arange(0.1, 5.1, 0.1)})
list_lambda = [-2, -1, -0.5, 0, 0.5, 1, 2]
for i, i_lambda in enumerate(list_lambda):
df_trans[ 'y'+str(i) ] = stats.boxcox( df_trans.x, lmbda = i_lambda )
fig, ax = plt.subplots()
ax.plot(df_trans.x, df_trans.y0, color='darkblue', label="lambda="+str(list_lambda[0]))
ax.plot(df_trans.x, df_trans.y1, color='mediumblue',label="lambda="+str(list_lambda[1]))
ax.plot(df_trans.x, df_trans.y2, color='skyblue', label="lambda="+str(list_lambda[2]))
ax.plot(df_trans.x, df_trans.y3, color='green',label="lambda="+str(list_lambda[3]))
ax.plot(df_trans.x, df_trans.y4, color='salmon', label="lambda="+str(list_lambda[4]))
ax.plot(df_trans.x, df_trans.y5, color='red', label="lambda="+str(list_lambda[5]))
ax.plot(df_trans.x, df_trans.y6, color='darkred', label="lambda="+str(list_lambda[6]))
ax.legend()
ax.set_title('y = Box-Cox( x, labmda )')
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.ylim(-10, 10)
plt.grid()
plt.subplots_adjust(left=0.15, right=0.95, bottom=0.1, top=0.9)
plt.show()
パラメータλ
次に気になるのは、パラメータλをどう決めたらいいのか。
scipyのドキュメント( https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.boxcox.html )によると、λは自分で与える必要はない。与えない場合は
If lmbda is None, find the lambda that maximizes the log-likelihood function
と記載されている。この記載だけでは分からないので、論文( https://www.ime.usp.br/~abe/lista/pdfQWaCMboK68.pdf )を読んだところ、要するに、
変換後の分布が最も正規分布(ガウス分布)らしくなるときのλを求めるということである。
Box-Cox変換とは、変数のスケールを変えて分布を正規分布(ガウス分布)の形に変えてくれる変換であることがわかった。
調査
Box-Cox変換についてなんとなく分かって気がしたところで、実際にある分布に対して変換を実行してみる。
変換前
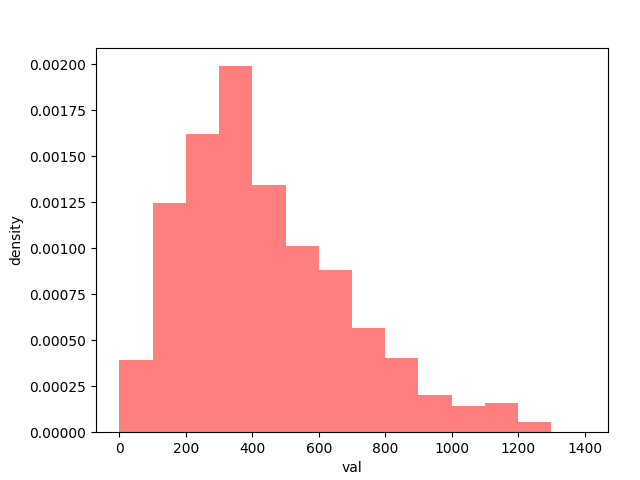
今回扱う分布は下図の通り。
横軸が変数valで、縦軸が規格化した行数(density)である。
変数valの値が大きい方に長いテールをもつような分布であることが分かる。
この分布をBox-Cox変換してみる。
分布を描画した際のコードは次の通り。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
df = pd.read_csv( 'data.csv', index_col=0, header=None, names=['val'] )
binlist=range(0, 1401, 100)
plt.hist(df['val'], bins=binlist, color='r', alpha=0.5, density=True)
plt.xlabel('val')
plt.ylabel('density')
plt.subplots_adjust(left=0.15, right=0.95, bottom=0.1, top=0.9)
plt.show()
変換後
元の分布の形状を左右対象の正規分布(ガウス分布)にするには、変換valが小さい領域のスケールを伸ばしつつ、大きい領域のスケールを縮めればよいので、λが0.5あたりになるのではと予想できる。
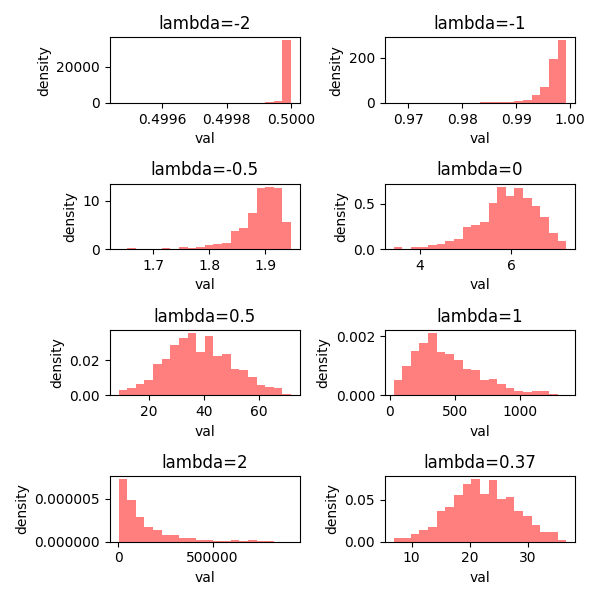
下図は、λを
[-2.0、-1.0、-0.5、0、0.5、1.0、2.0]と与えて変換した場合に加えて、λの値を指定しないで変換した場合、合計8個の分布を示している。
パラメータλを指定しないで変換した場合、$λ = 0.37$となり、予想とおおよそ一致し、左右対象の正規分布(ガウス分布)らしい分布に変換されたことが分かった。
上図を描画した際のコードは次の通り。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
fig = plt.figure(figsize=(6.0, 6.0))
list_lambda = [-2, -1, -0.5, 0, 0.5, 1, 2]
for i, i_lambda in enumerate(list_lambda):
df[ 'val_'+str(i) ] = stats.boxcox( df.val, lmbda = i_lambda )
fig.add_subplot(4, 2, i+1).hist(df['val_'+str(i)], bins=20, color='r', alpha=0.5, density=True)
plt.title("lambda="+str(list_lambda[i]))
plt.xlabel('val')
plt.ylabel('density')
df[ 'val_auto' ], best_lambda = stats.boxcox( df.val )
fig.add_subplot(4, 2, 8).hist(df['val_auto'], bins=20, color='r', alpha=0.5, density=True)
plt.title("lambda="+str(round(best_lambda, 2)))
plt.xlabel('val')
plt.ylabel('density')
fig.tight_layout()
fig.show()
plt.show()
まとめ
Box-Cox変換が何者か理解できた。
図を描画する際に参考にした。