これ書くだけで土日2日間まるまる潰れてしまった。
学んだ内容に沿っているので、順に読み進めるに従ってコードの話になっていきます。
Tensorflow触ってみたい/みたけど、いろいろまだ理解できてない!という方向けに書きました。
※2018年10月4日追記
大分古い記事なのでリンク切れや公式ドキュメントが大分変更されている可能性が高いです。
この記事のTensorflowは ver0.4~0.7くらいだった気がするので ver2.0~となりそうな現在は文章の大半が何を参考にしているのか分からないかもしれません。
1: Deep Learningってそもそも何してるの?
専門の人からはご指摘入りそうですが、要は回帰分析してくれるブラックボックスと言い切ってはどうでしょう。
"回帰"という単語が出てくるだけで ?が出てきちゃいますよね。
求めたい"値"があってそれに限りなく近い数値を機械に計算させまくり学んでもらう。で、いいんじゃないでしょうか。
eg.適度な関数が知りたい
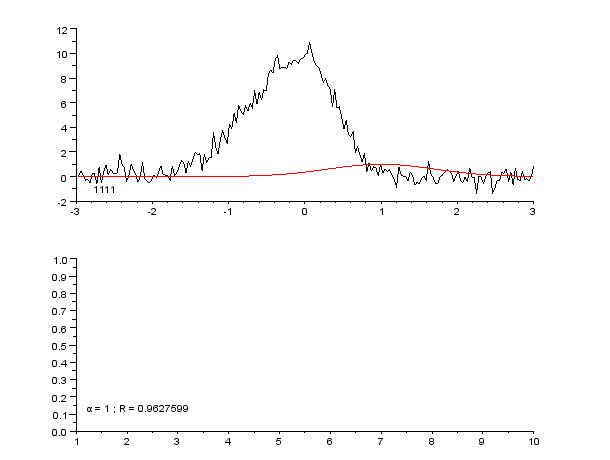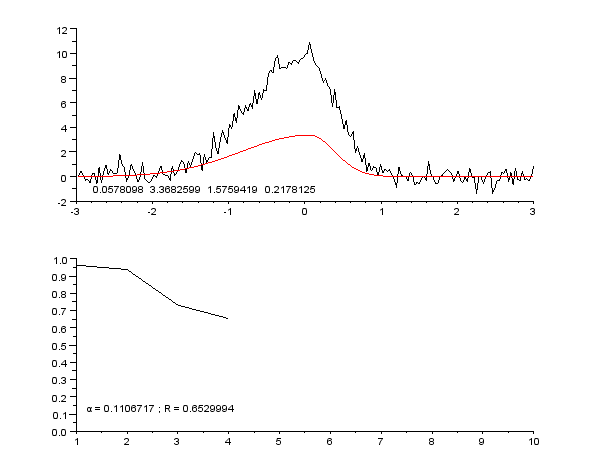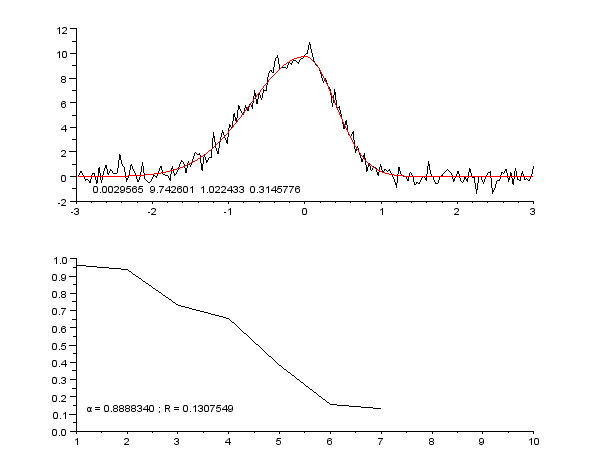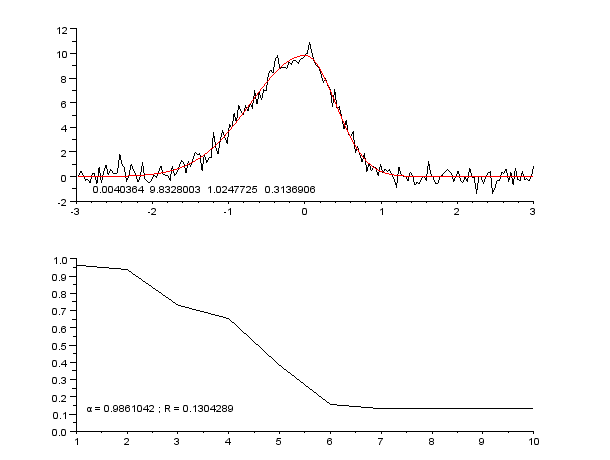
eg.適度なクラスターを知りたい
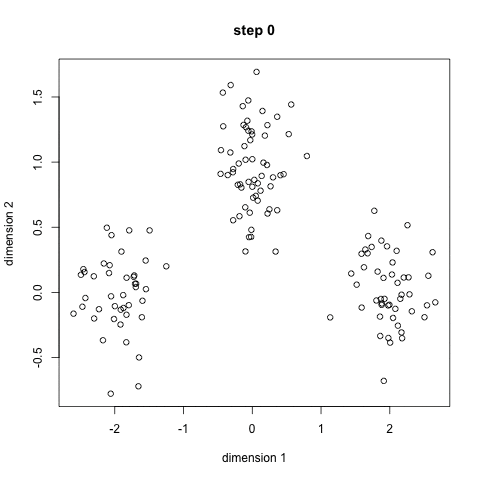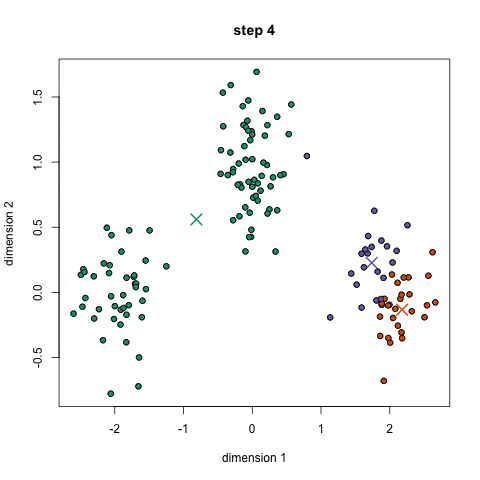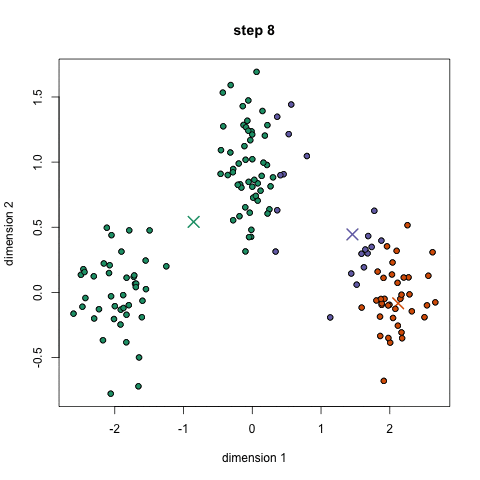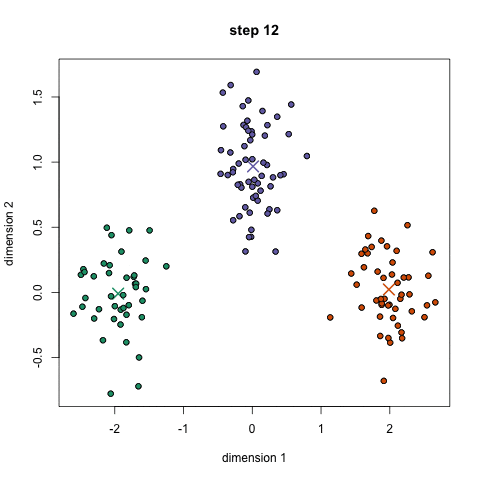
eg.適度な"顔"というものをpixelの集合で知りたい

それなら自分だって知りたいことはたくさんあるよ!という方々は多いと思います。
アイドルの動画からすげーブサイクな顔になってる時(値)だけを求めて、キャプチャしたい!とか、Qiita: - ディープラーニングで顔写真から巨乳かどうかを判別してみる (うまくいったか微妙)だとか。
偉大なる先人達は常にいるようですね。
というわけでDeep Learning始めてみよう!となりました。
2: フレームワーク選び - Tensorflowの良いところ
結論から先に言うと情報量
最初の方はTensorflowの中身やら関数が何やってるか分からないので、途中Theanoに乗り換えを何度も考えましたが、今のところは大抵の疑問はすでに(英語で)Stackoverflowにあったり、Githubのイシューにも色々書いてあるので、やっぱりGoogleのネーム力って凄い。 Tensorflow本体のコードも普通に関数名でgoogle検索したりすると出てくるので、使ううちにどんどん本体の理解が勝手に深まります。
そもそも触り始める前はなにができて、なにができないのか?も分かっていない状態だったので、Deep Learning系フレームワークで色々な実験をされている方々のブログを読み漁りました。
ドキュメントの分かりやすさなどは Tensorflow > Theano > Chainerですかね。
その他に:
- Caffe
- 元GoogleのAndy Rubinが投資しているNervana
- GUIベースのドラッグ&ドロップで機械学習とかできちゃうMicrosoft Azure Machine Learning
などなど見てみました。
ただ中身の評価モデルなどを理解していない段階だとなにもできません。 なので結局情報が一番ありそうなTensorflowでスタートしました。
多分この分野に慣れてくると評価モデルの関数がたくさん用意されているとかが主な使用理由になるのではないでしょうか。
※2016/4/26追記
日々githubにコミットされていく内容とかを追っていると、もうTensorflow以外はしばらく様子見でいいんじゃないかなぁーと思います。
読み漁ったブログ一覧
-Tensorflow
kivantium活動日記: - TensorFlowでアニメゆるゆりの制作会社を識別する
すぎゃーんメモ: - TensorFlowによるディープラーニングで、アイドルの顔を識別する
-Theano
人工知能に関する断創録: - Theanoによる畳み込みニューラルネットワークの実装 (1)
StatsFragments: - Theano で Deep Learning <3> : 畳み込みニューラルネットワーク
-Chainer
せかいらぼ: -LSTMで自然な受け答えができるボットをつくった
Oriental Robotics: - RNNによる学習で文豪っぽいテキストを出力させる (aka DeepDazai)
Preferred Research: - 分散深層強化学習でロボット制御
3: Hello, World!的なMNIST ビギナー編
※インストール的な話は沢山出てるので飛ばします。
※※ビギナーチュートリアルを読んでからがオススメです。
ここから真面目な解説スタートです。
機械学習のベンチマーク的なものMNIST。
Tensorflowの最初のチュートリアルとして 0〜9の手書き数字画像を大量に与えて、数字を理解させる練習です。
ビギナーもエキスパートもコピペすれば動くのですが... ここで学ぶべきことは直接のコードというより、Tensor, Rank, Scalar, Vector (テンソル、ランク, スカラー、ベクトル, シェイプ)などTensorflowにおける概念や処理、そして数学的な理解の再確認でした。
まずは一番重要なTensorについて。
入力となるデータなどを取り扱ってくれる頼りになるTensorはあくまでデータ構造で、学習処理の間でやりとりされるだけです。 Tensorはn次元の配列もしくはPython的にはlistと考えるのが良いそうな。
学習のバッチ毎にTensorの中にデータを入れてあげる感じですね。
なので学習処理以外の時にprint hoge_Tensorなんてしてみても中身は入ってないんです。
"重み"など学んでいく過程の値はtf.Variable変数で持ち続けます。
そしてTensorにはRank, Shape, Typeが必ずあります。
エラーでよく言われるので、理解してからはだいぶ楽になりました。
Rank
t = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] はRank2
要はTensor自身の次元数ですね。
| Rank | 数学単位 | Python example |
|---|---|---|
| 0 | Scalar (実数量のみ) | s = 483 |
| 1 | Vector (量と方向) | v = [1.1, 2.2, 3.3] |
| 2 | Matrix (よくあるテーブル) | m = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] |
| 3 | 3-Tensor (三次元) | t = [[[2], [4], [6]], [[8], [10], [12]], [[14], [16], [18]]] |
| n | n-Tensor (n次元) | .... |
Shape
先のt = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] Shapeは3次元x3次元なので[3, 3]
| Rank | Shape | Dimension number | Example |
|---|---|---|---|
| 0 | [] | 0-D | A 0-D tensor. A scalar. |
| 1 | [D0] | 1-D | A 1-D tensor with shape [5]. |
| 2 | [D0, D1] | 2-D | A 2-D tensor with shape [3, 4]. |
| 3 | [D0, D1, D2] | 3-D | A 3-D tensor with shape [1, 4, 3]. |
| n | [D0, D1, ... Dn-1] | n-D | A tensor with shape [D0, D1, ... Dn-1]. |
Type
これはintやらfloatなので、あまり説明はいりません。
MNISTでそれらTensorを見る
MNISTの例で言うと、55000枚の画像データ(images)Tensorと画像の答え(labels)Tensorがでてきます。
Images Tensorは Shape[55000, 784], Rank2, dtype=tf.float32
Labels Tensorは Shape[55000, 10], Rank2, dtype=tf.float32
チュートリアルではtf.placeholderでまず挿入されています。(Tensor確保と言った方がわかりやすいかも)
x = tf.placeholder(tf.float32, [None, 784]) #images
y_ = tf.placeholder(tf.float32, [None, 10]) #labels
# None部分にはバッチの数が入る
なおtf.placeholder()は学習実行毎に必ずfeed_dict引数でデータを与えてもらう必要があります。
チュートリアルの場合は最後の方で学習実行開始するのですが:
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
なので、実際にはTensor達はx:Shape[100, 784] y_:Shape[100, 10]の画像100枚ごとに処理されてますね。
余談: 画像の次元数について
画像データの方はもともと28x28pixelsのグレースケール = 1 channelですが、ビギナーチュートリアルでは簡単に考えるため784次元のベクトルにフラット変換(というか既にされてます。)
28281 = 784-Dimension
- 図で見るとなんとなくわかる -
縦横に並んでる数字を全部横にする的な。
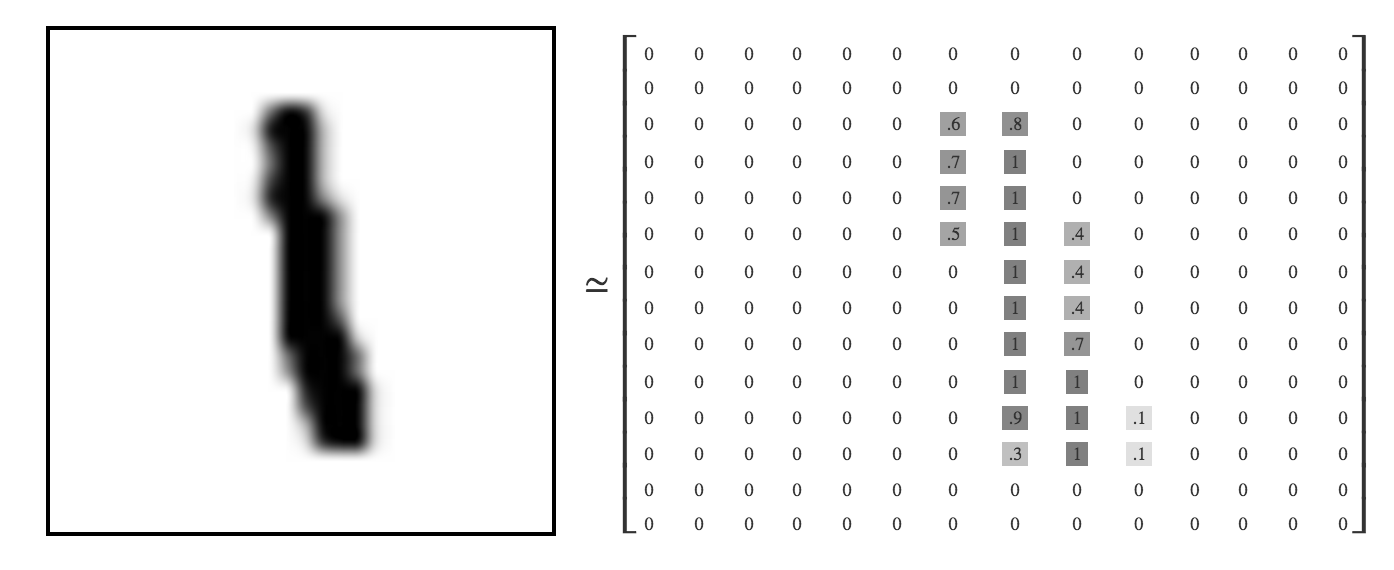
00000000000000000000000000000000000000000000000000000000000000000000000000000000000000.6.7.7.50000000000.81111111.9.30000000.4.4.4.7111000000000000.1.10000000000000000000000000000000000000000000000000000000000
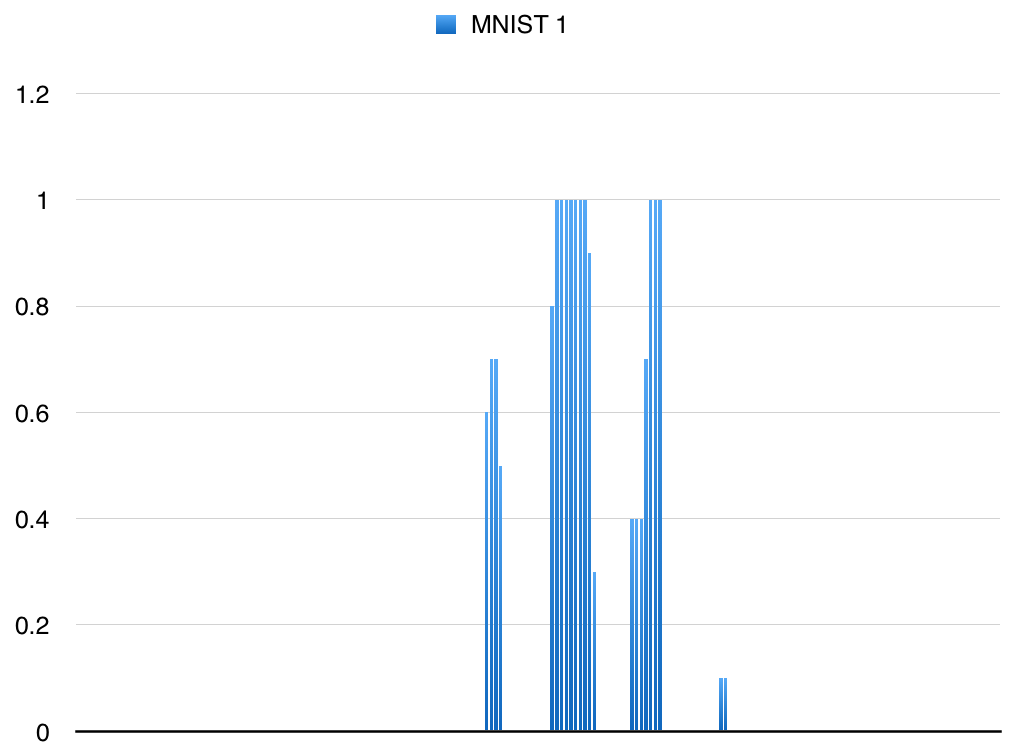
見える人には"1"に見えるらしい。
ちなみに画像をフラット化しない[55000, 28, 28, 1]の場合はRank4
カラー画像の場合でも3 channelsに変わるだけなので[55000, 28, 28, 3] Rank4
4: Tensorflowの処理: - ビギナーチュートリアルでしていること
さてさて、Tensorが理解できた所でやっとTensorflowの機械学習的な処理が追えるようになります。
用意したImage Tensorx:[batch_num, 784]ですが、784次元ベクトルから一体どうやって10通りある正解の中から正確な答えを導き出すのでしょうか?
ここで行列演算と"重み", "バイアス", Softmax回帰 4つの存在を理解します。
行列演算
行列演算は簡単な話です。
x:[batch_num, 784]に[784, 10]の行列演算をすると[batch_num, 10]の行列が生まれるので答えが10通りになります。
wikipediaの画像を参考にすると;
A:[4,2]とB:[2,3]が[4,3]になっています。
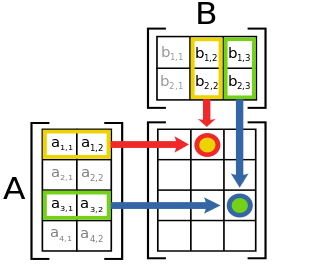
Tensorflowでいうと
tf.matmul(A,B) # A is [4,2] and B is [2,3]. output would be [4,3]
'''
x: [batch_num, 784]
W: [784, 10]
matmul: [batch_num, 10]
'''
matmul = tf.matmul(x,W)
このB[2,3]、MNISTでいうとW:[784, 10]が重要な重みとなります。
重み
重みW:[784, 10]が登場しました。 コードでいう部分は
W = tf.Variable(tf.zeros([784, 10]))
tf.Variable()はin-memory buffersということで、学習に使いたいパラメーターが保持されつづけるTensorを含んだ変数です。
tf.zeros()は中身をすべて0で埋めているTensorを作ります。
0で埋めているのは学習の過程で随時アップデートされるので、0スタートなだけです。ランダムな数値を入れるtf.random_normal()もあります。
重みの役割
W:[784, 10]の中身は画像が持つ1pixel単位の数値に、0の可能性は0.XXX, 1の可能性は-0.XXX, 2の可能性は0.0XX....といった感じで数値を掛け合わせにきます。
例えば先の"1"の画像の場合、一番最初の左上のピクセルに対しては、実際の学習させた重みW[0]は[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]なことが多いです。理由は明快で0〜9の全数字でその左上ピクセルが意味をなすことがないからです。
ど真ん中あたりの重みW[380]を見てみると:
[-0.23017341 0.03032022 0.02670325 -0.06415708 0.07344861 -0.05119878 0.03592584 -0.00460929 0.09520938 0.08853132]
となっています。 0の重み-0.23017341がマイナスということはつまり**ど真ん中のピクセルが黒い時に”0”の可能性は低い。**ということが理解できます。

エキスパートチュートリアルの畳み込み層などの話になるとより思うのですが、個人的には重みというよりフィルターという言葉が一番しっくりする気がしている。
この重みをImages Tensorに行列演算すると
matmul = tf.matmul(x,W)
print "matmul:", matmul[0] #最初の画像(答えは7)
matmul: [ 1.43326855 -10.14613152 2.10967159 6.07900429 -3.25419664
-1.93730605 -8.57098293 10.21759605 1.16319525 2.90590048]
が返ってきます。
うーん、まだよくわかりませんね。
バイアス
バイアスはすごい感覚で言うため不適切かもしれないですが、
y = x(sin(2+(x^1+exp(0.01)+exp(0.5)))+x^(2+tan(10)))+x(x/2x+x^3x)+0.12
みたいな関数があった場合の最後の0.12みたいなものでしょうか。
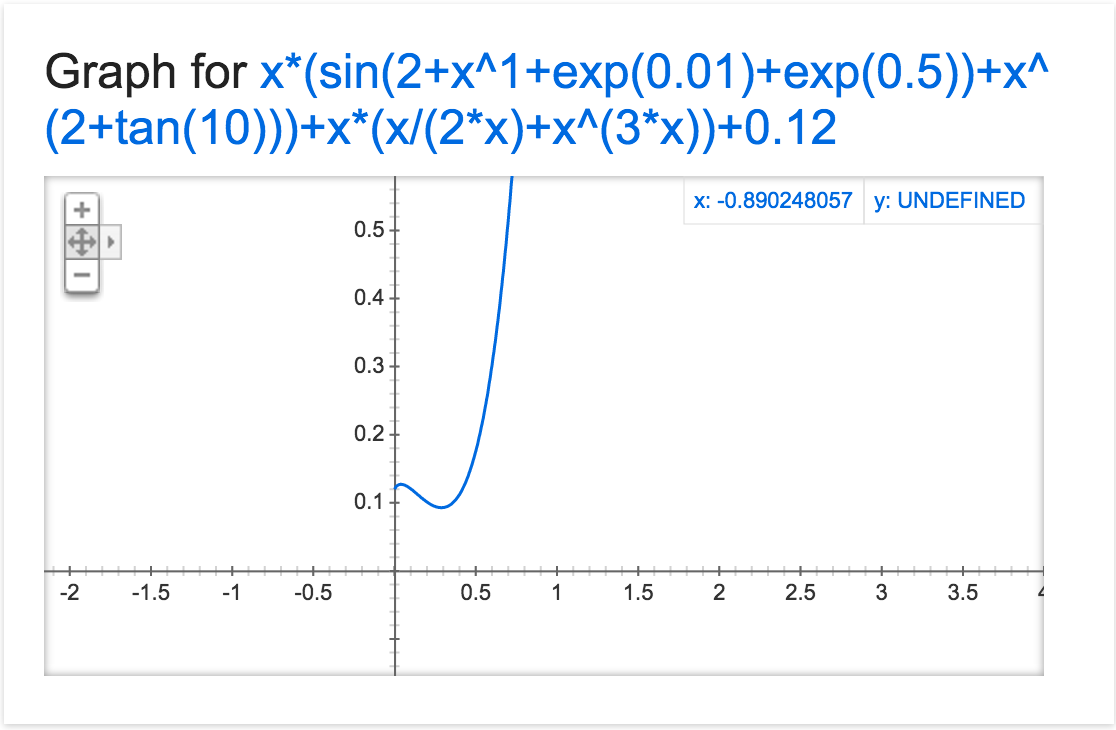
もっと簡単にいうとy = xa + bのb?
あっ、だからbiasなんですかね。
ただチュートリアルの場合はバイアスなしでも答えの精度はあまり変わりませんでした。
仮にバイアスの真値がb = 1e-10とかだとあまり意味ないのかもしれませんね。
コードでは重みと同じように作ってあげますが、画像Tensorと重みはすでに行列演算されているため、後から付け足すバイアスはRank1のShape[10]です。
b = tf.Variable(tf.zeros([10]))
print "b:",b #学習後のバイアス
b: [-0.98651898 0.82111627 0.23709664 -0.55601585 0.00611385 2.46202803
-0.34819031 1.39600098 -2.53770232 -0.49392569]
こっちもこれ単体だとよくわかりませんね。
Softmax関数 - 答え合わせ -
元のImages Tensor x:[batch_num, 784]は、
x 重みW:[784, 10]と行列演算され
= matmul:[batch_num, 10]になった後、
+ バイアスb:[10]を付け足されてしまいます。
しかし、それなのにいまだこれら数値が示す意味がわかりません。
そこでこれらをtf.nn.softmax()に渡して人でもわかるような数値にさせます。
y = tf.nn.softmax(tf.matmul(x, W) + b)
print "y", y[0] #最初の画像(答えは7)
y [ 2.04339485e-05 6.08732953e-10 5.19737077e-05 2.63350527e-03
2.94665284e-07 2.85405549e-05 2.29651920e-09 9.96997833e-01
1.14465665e-05 2.55984633e-04]
見てみると7番目の数値が一番高いですね。どうやら7の確率が高そうです。
配列の中の確率というより単純に答えを合わせをしたい場合は
x_answer = tf.argmax(y,1)
y_answer = tf.argmax(y_,1)
print "x",x_answer[0:10] #Tensorflowが思う最初の10画像の答え
print "y",y_answer[0:10] #10画像の本当の答え
x [7 2 1 0 4 1 4 9 6 9]
y [7 2 1 0 4 1 4 9 5 9]
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print "accuracy:", accuracy
accuracy: 0.9128
※2016/05/19追記
Softmax関数はアービタリーな実数値のまとまりをrange(0, 1)に押し潰してくれる関数です。
最初Softmax回帰と書いていたんですが、正確には確率に対する回帰を行うので"ロジスティック回帰"と呼ぶそうな。 Softmaxはあくまでも入力を入れると出力が帰ってくる関数なんですね。
MNISTは画像を分類する問題なので一連の処理としては、
"この画像に対する各ラベルの確率が知りたい" → "ロジスティック回帰(softmax)" → "一番確率が高いものを答えとする(argmax)" となります。
なので実数値を求めたい回帰分析の場合はsoftmaxを多分使いません。
5: いつ学習しているの?
TensorflowがMNISTの答えを出してくれるまでの仕組みがこれで理解できました。
でも重みWやバイアスbの学習はどうやって進んでいるの?となりますよね。
ヒントはTensorflowの学習実行が繰り返される部分にあります。
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
このtrain_stepがどうやらトレーニングしていそうです。中身は
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)
'''
y: [batch_num, 10] y is a list of processed numbers of x(images)
y_: [batch_num, 10] y_ is labels
0.01 is a learning rate
'''
となっていますが、もう少し噛み砕いてみましょう
tf.log()はわかりやすくlogを計算します。Tensor自体に変化はないのでlog-y:[batch_num, 10]です。
そして答えTensory_と掛け合わせるのですが、y_は答え以外は全て0が入っているため掛け合わせると答え以外のindexは値が0になります。
掛け合わさったTensorもShapeは[batch_num, 10]ですが、答え部分以外は0のため実質的な次元は[batch_num, 1]と考えたほうがわかりやすいかもしれません。
log-y = tf.log(y)
print log-y[0]
[ -1.06416254e+01 -2.04846172e+01 -8.92418385e+00 -5.71210337e+00
-1.47629070e+01 -1.18935766e+01 -1.92577553e+01 -3.63449310e-03
-1.08472376e+01 -8.88469982e+00]
y_times_log-y = y_*tf.log(y)
print y_times_log-y[0] #7の値のみが残る。
[-0. -0. -0. -0. -0. -0.
-0. -0.00181153 -0. -0. ]
tf.reduce_sum()は次元間すべてでの加算を行い、第2引数とkeep_dims=Trueオプションがない場合はRank0のTensor(スカラー)になります。 MNISTの場合は[batch_num]の保有する値を全部足した数ですね。
# 'x' is [[1, 1, 1]
# [1, 1, 1]]
tf.reduce_sum(x) ==> 6
tf.reduce_sum(x, 0) ==> [2, 2, 2]
tf.reduce_sum(x, 1) ==> [3, 3]
tf.reduce_sum(x, 1, keep_dims=True) ==> [[3], [3]]
tf.reduce_sum(x, [0, 1]) ==> 6
------
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
print "cross_entropy:", cross_entropy #y_*tf.log(y)の中身を全部足した数
cross_entropy 23026.0 #最初の学習後の数値
.
.
.
cross_entropy: 3089.6 #最後の学習後の数値
クロスエントロピーについてはこちらの記事がとても参考になります。
ニューラルネットワークと深層学習: -無料のオンライン書籍- チャプター3
http://nnadl-ja.github.io/nnadl_site_ja/chap3.html
要はどれだけ学習できているかの指標的なものですかね。
これを参考にしつつ重みやバイアスを最適化していけば学習成功のようです。
実際の最適化を行っているtf.train.GradientDescentOptimizer()ですが、他にも選べるチョイスclass tf.train.Optimizerがありますので、一度見てみるのも楽しいです。
Tensorflow/api_docs - Optimizers:
https://www.tensorflow.org/versions/r0.7/api_docs/python/train.html#optimizers
追加で.minimize()を呼ぶとGradientの計算とtf.Variablesへの適用を一緒に行います。
逆に.compute_gradients()を呼ぶことで最適化の際に重みWやバイアスbをアップデートするための値、つまりは誤差値/修正値をみることができます。
実際には±大きな数値でスタートしてアッチコッチ行ったり来たりしながら収束していくみたいです。
# 学習初期
cross_entropy 23026.0
grad W[0] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
grad W[380] [ 511.78765869 59.3368187 -34.74549103 -163.8828125 -103.32589722
181.61528015 17.56824303 -60.38471603 -175.52197266 -232.44744873]
grad b [ 19.99900627 -135.00904846 -32.00152588 -9.99949074 18.00206184
107.99274445 41.992836 -27.99754715 26.00336075 -8.99738121]
# 学習最後
cross_entropy 2870.42
grad W[0] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
grad W[380] [ 6.80800724 1.27235568 -6.85943699 -22.70822525 -17.48428154
13.11752224 19.7425499 -32.00106812 -41.48160553 79.59416199]
grad b [ 19.52701187 3.17797041 -20.07606125 -48.88145447 -28.05920601
37.52313232 40.22808456 -34.04494858 -74.16973114 104.77211761]
重みWに関しては最初のピクセルは完全に無視してるみたいですね...笑
これらの数値はまぁ機械に計算を任せて、我々はゆっくりお茶でも飲んでいるのがいいのではないでしょうか。
6: 次回はエキスパートを詳しく解説するよっ!
私自身がやりたいことは実はまだ実現できていないのですが... 機械学習は"モノづくり心"を超刺激してくれるのですっかり魅了されてしまいました。 理解が深まるほど、次は"こうしてみよう"、"あーしてみよう"とアイデアが出てきます。
うまくいかないけど楽しい。 なんだろう...この懐かしい感じ。
次はチュートリアルのMNIST エキスパート編を解説したいと思います。
畳み込み、プーリングなどがイマイチわかっていない方にはオススメの内容にしたいです。
ストック、ツイート、いいね、はてぶ、コメントなどなど、全て励みになるのでもしよければお願いします〜。
※2016.3.29追記
エキスパート編の解説書きました。
-
Tensorflowを2ヶ月触ったので"手書きひらがな"の識別95.04%で畳み込みニューラルネットワークをわかりやすく解説
※2016.12.08追記
Advent CalenderでLSTMの解説を書きました。
これを理解できれば自然言語処理もできちゃう? MNISTでRNN(LSTM)を触りながら解説