師走に調子乗ってTensorflow Advent calendar 2016登録して完全にヒーヒー言いながら今回の内容を書きました。おそらく後から読みやすいように追記や更新もすると思います。8日目です。どうも。

この記事はTensorflowのチュートリアルを読んでなんとなくの機械学習的な理解がある方達がおそらく対象です。
それらに関連した解説も一応書いてます。

・ビギナーの解説 : 特にプログラマーでもデータサイエンティストでもないけど、Tensorflowを1ヶ月触ったので超分かりやすく解説
・エキスパートの解説 : Tensorflowを２ヶ月触ったので"手書きひらがな"の識別95.04%で畳み込みニューラルネットワークをわかりやすく解説

機械学習がどんどん盛り上がってますね。　みなさん楽しそう。
そんなわけで今更word2vecなんてやっても...感もあるので、すっ飛ばしてReccurent Neural Network(RNN)やりましょう、今更。

RNNといっても色々柔軟性たかそうなLSTMにしました。扱うデータも文章だとややこしくなるのでMNISTです。レポジトリはこちらを使います。
Github: TensorFlow-Examples/recurrent_network.py

実は過去にはプチRNNでカオスの回帰というのやったりしたのですが、やはり過去の情報から未来を予測しようとした時に、ただ単に過去の情報を引き継ぐだけだとそのうち限界がくるみたいで。 LSTMなら適度に忘れたり覚えたりしてくれるみたいなので良さげです。

1.今回よく使う用語 :

いきなり説明し始めると私自身も支離滅裂になってしまうので、(私的解釈な)用語を説明しておきます。

input : 入力情報　今回の場合は例の如く画像のピクセル達グレースケールの0〜1で表現されているやつです。
output : 出力結果　あくまでもRNNから吐き出されるものなので最終的な答えとは限らない。次の入力情報と合わせて再利用もされる。
cell state: 内部状態　前回までの入力情報&予測結果などを考慮して今の考えてる状態を保持してる人
sigmoid (σ): シグモイド　覚えるか・忘れるかなど判断してくれるやつ
tanh: ハイパボリック・タンジェント　内部状態 -> 予測結果や、入力情報->内部状態などのシーンで使われる活性化関数。
weight: 重み　　機械学習の様々な場面で登場する奴らtf.Variable。主にこれを学習させる。
bias: バイアス　　出力を微調整してくれるやつ。　最近存在感が薄い

2.RNNで大事なのはループ構造と内部状態

Recurrent(循環, 回帰性)というくらいなので、RNNは情報を再利用します。　有名な Christopher Olahさんの記事から図を参考にさせていただきますが、基本的には内部の状態というものがあってそこから出力結果を出します。

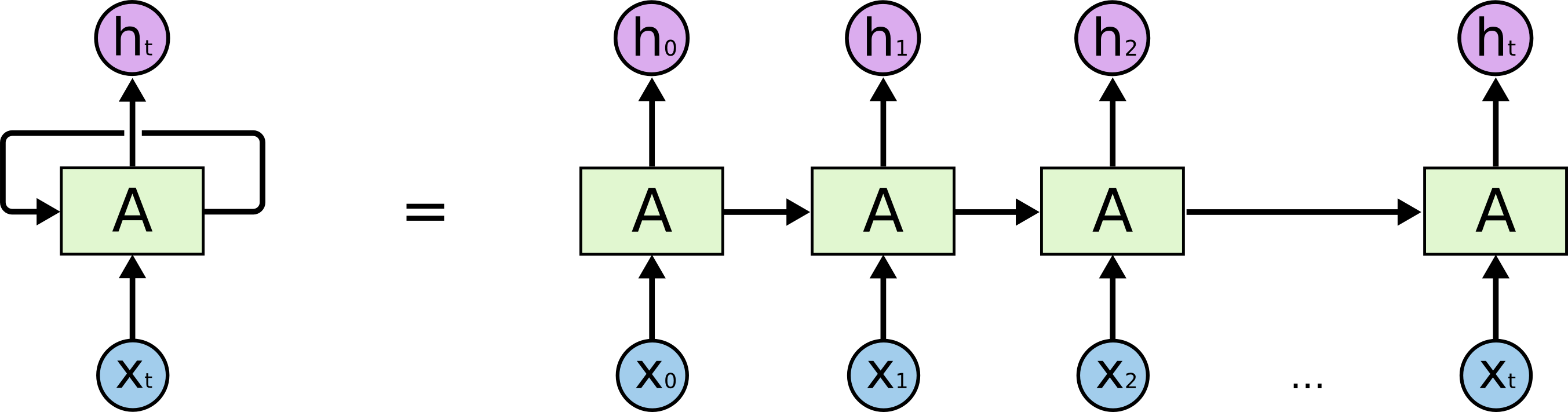
感の良い方は図を見て気づくかもしれません。　通常のRNNだと情報の取捨選択をしないので、このループの長さが長くなればなるほど過去の情報の特徴が内部状態の中で薄れてしまうんです。
つまり単純にループさせるだけではダメで、入力->内部->出力のパイプラインをクリエイティブに作らなくてはいけないのです。　

頭の良い人たちはきっとこう思ったのでしょう。"時系列データで答えを出すには情報の取捨選択が必要だ。でも特徴は内部状態に保持し続けたい。"
そこでLSTMでは

ループ構造による情報の再利用
情報選択のシグモイド
特徴保持の内部状態
などが出てきます。

3.ループの構造 : 入力から出力までの流れ

音声やら文章やらの時系列データなどで活躍するRNNは、前の出来事と今回の出来事を比べた上で次の現象はなんじゃらほい？と考えてくれるんですね。
じゃあMNISTみたいな数字の画像でどうやって前の出来事と今回の出来事比べるのでしょう？　時系列データではないじゃないですか先輩。と思う方もいると思います。でもMNISTのビギナーでも画像を一列に並べるという荒技を使っているので、世の中考え方を変えればどうとでもなるみたいですよ。

画像データを時系列として扱うには、ハサミで紙を切り刻むように、28回続く28次元ベクトルとして扱います。 CNNの28x28ピクセルのマトリックスと似たようなものでしょうか。空間的な縛りは無くなりますが。

イメージとしてはこんな感じ?

コードで見ていきましょう。

LSTM.py

n_input = 28
n_steps = 28
n_hidden = 128
batch_size = 50
x = tf.placeholder("float", [None, n_steps, n_input]) # Noneはバッチサイズが入る。つまり [50, 28, 28]

def RNN(x, weights, biases):
  x = tf.transpose(x, [1, 0, 2])  #[28, 50, 28]のtensor
  x = tf.reshape(x, [-1, n_input]) #[28*50, 28]のtensor
  x = tf.split(0, n_steps, x) #[50*28] 28 tensors (sequences)
  lstm_cell = rnn_cell.BasicLSTMCell(n_hidden, forget_bias=1.0)
  outputs, states = rnn.rnn(lstm_cell, x, dtype=tf.float32) 
  #outputs [28,50,128]  states [28,50,128]  つまり [n_steps, batch_num, hidden_vectors] 
  return tf.matmul(outputs[-1], weights['out']) + biases['out']

入力情報がものすごいごにゃごにゃされてますね...
最初のtransposeでshapeを入れ替えたのは考えなくてもわかるのですが、Tensorflowの性質上、RNNCellというものはシーケンスの数だけtensorを作ってあげないといけないらしいために tf.split()でこのようなShape[50, 28]のTensor x 28個にしないといけないようです。

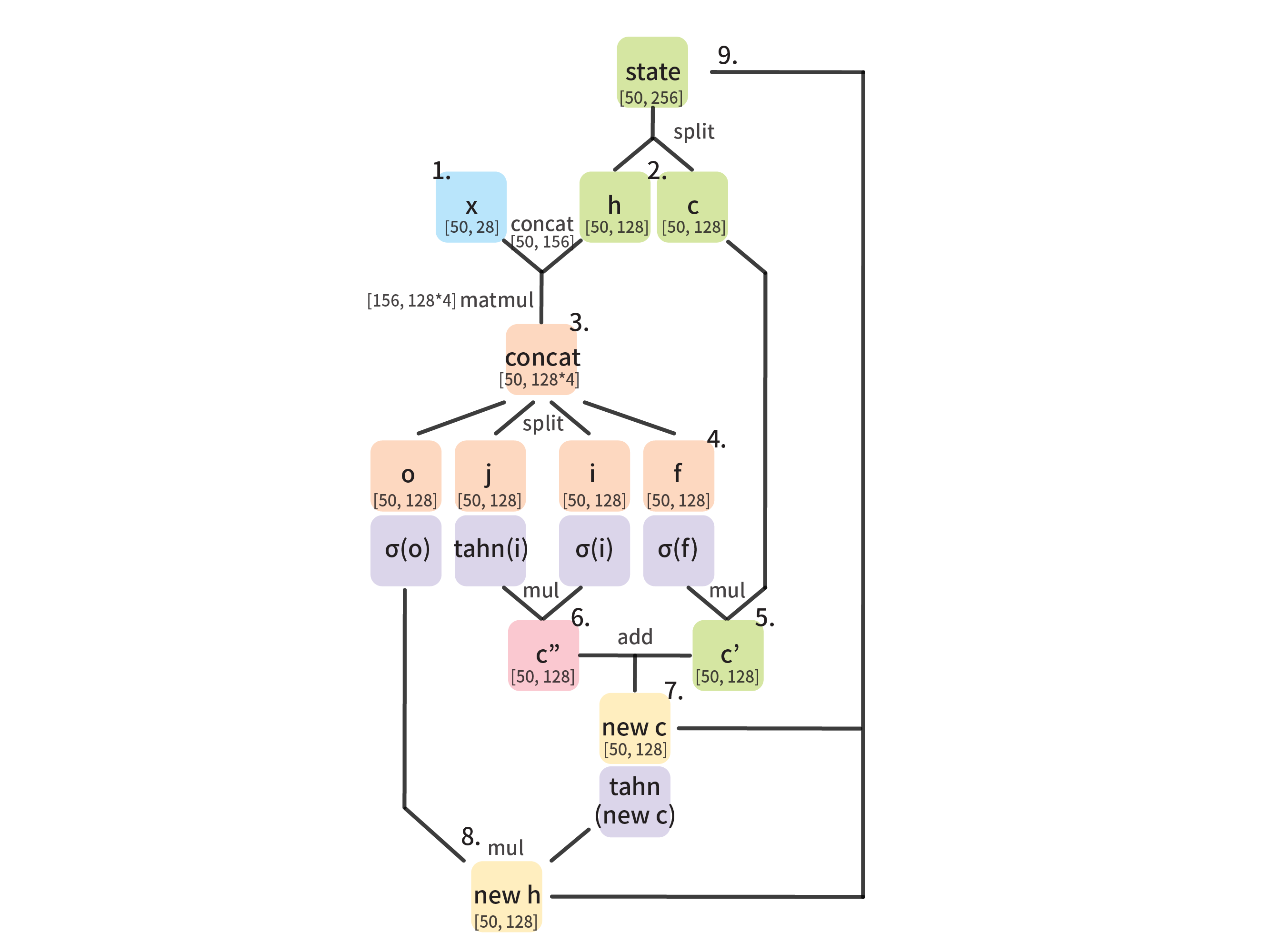
そしてその後は謎のtf.nn.rnn_cell.BasicLSTMCell()とtf.nn.rnn()が出てきました。こいつの中身を知らないとループ構造を語ることは難しそうです。ここら辺に書かれてます

抜粋-rnn_cell_impl.py

class BasicLSTMCell(RNNCell):
.
.
.
 def __call__(self, inputs, state, scope=None):
    """Long short-term memory cell (LSTM)."""
    #num_unit = n_hidden = 128
    #inputs = x [50, 28]*28 tensors
    #activation is tanh
    with vs.variable_scope(scope or "basic_lstm_cell"):
      # Parameters of gates are concatenated into one multiply for efficiency.
      if self._state_is_tuple:
        c, h = state
      else:
        c, h = array_ops.split(1, 2, state)
      concat = _linear([inputs, h], 4 * self._num_units, True, scope=scope) #[batch*output_size]

      # i = input_gate, j = new_input, f = forget_gate, o = output_gate
      # each parameter is [50, 128]
      i, j, f, o = array_ops.split(1, 4, concat)

      new_c = (c * sigmoid(f + self._forget_bias) + sigmoid(i) *
               self._activation(j))
      new_h = self._activation(new_c) * sigmoid(o)

      if self._state_is_tuple:
        new_state = LSTMStateTuple(new_c, new_h)
      else:
        new_state = array_ops.concat(1, [new_c, new_h])
      return new_h, new_state

見た感じ上のoutputsにはnew_hが statesにはnew_cとnew_hを合わせたものが入ってそうです。hが出力結果 cが内部状態
なので一連の流れとしてまとめると

xのシーケンスno.1が[50, 28]のshapeで投下される
前回の内部状態cと出力結果hを生成ただしシーケンスno.1だと初期化なのでまっさらな0
xとhをconcatしてさらにn_hidden*4の重みで行列演算する
3で誕生した[50, n_hidden*4]のtensorを４分割し、 i = input_gate, j = new_input, f = forget_gate, o = output_gateとする。
c * sigmoid(f)でシグモイドでcの中の忘れるもの決めて、忘れさせる
sigmoid(i)*tanh(j)でシグモイドで新しい情報として覚えるもの(cに渡すもの)を決め、tahn活性化させる
5と6を足し合わせると新しい内部状態 new_cが完成
新しい内部状態があれば結果を出力できるので、tahn(new_c)*sigmoid(o)で内部状態を活性化させさらにシグモイドでフィルタリングし new_hが完成
new_cとnew_hを合わせたものがシーケンスno.2のc hとして再利用される

言葉で言うと難しいので図にして見た

このループ構造から最後にでた出力結果outputs[-1]を
tf.matmul(outputs[-1], weights['out']) + biases['out']
と行列演算してさらにその後softmaxを通すことでやっと答えになります。

なので -よく使う用語- の項目でも書きましたが RNNの出力結果は必ずしも答えではない、と言うことになります。　他のRNNを連結したりもするらしいので適度なベクトルで留めておきたいのでしょうね。

さて、このループ構造が肝でいかに内部状態を作ることが非常に重要なのだけど、その内部状態を作るのにどうやらシグモイドがすごい頑張っているように見えますね。

4.何を覚える/忘れるか情報選択をしてくれるシグモイド

シグモイドがなぜ覚える・忘れる機能として使われるかと言うと...
図で見てみましょう

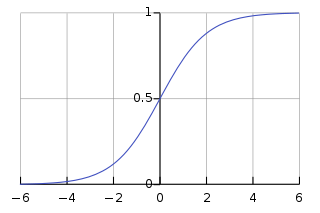
シグモイドを通してあげると数値が0〜1に収まるのです。と言うことは入力情報のベクトルxなどに重みをかけてからこの関数を使うと、忘れたいものは0覚えていたいものは1に近づくという風に機能します。その0〜1になったベクトルと内部状態のベクトルを掛け合わせると、都合よく情報選択された状態に変化します。

実際にどのように変化するのか見てみたいですね。rnn_cell_impl.pyに書いてあるBasicLSTMCellの中身から直接変化を見れるようにしたかったですがうまくいじれなかったので、同じMNISTでここに出てくる10次元のベクトルに行列演算された7の画像の配列を使ってみます。
[ 1.43326855 -10.14613152 2.10967159 6.07900429 -3.25419664 -1.93730605 -8.57098293 10.21759605 1.16319525 2.90590048]

これをシグモイドに通すとこうなります。

sigmoid_test.py

test = tf.sigmoid(tf.constant([1.43326855, -10.14613152, 2.10967159, 6.07900429, -3.25419664, -1.93730605, -8.57098293, 10.21759605, 1.16319525, 2.90590048]))

test [  8.07410061e-01   3.92260008e-05   8.91839623e-01   9.97714758e-01
   3.71763781e-02   1.25944108e-01   1.89490354e-04   9.99963522e-01
   7.61912763e-01   9.48137343e-01]

#e-01とかだとわかりづらいので

test [  0.807410061   0.0000392260008   0.891839623   0.997714758
   0.0371763781   0.125944108   0.000189490354   0.999963522
   0.761912763   0.948137343]

といった感じで一番数値の大きかった7番目の10.21759605が0.999963522と限りなく1に近づいています。逆に一番数値が低い2番目の-10.14613152も0.0000392260008と限りなく0に近づいてますね。 (このレベルの桁数はあくまでも人間的な限りなくですが)

解釈するなれば7,4,9あたりは特に覚えておいて2,6,5あたりはあまり気にしないようにする。といった感じでしょうか。　

今回のLSTMのループ構造内では実際には10次元のベクトルではなく、隠れ層128次元のベクトルとしてもう少し細かく情報の取捨をしています。LSTMでsigmoid(f)*cなどとしているのはcの中身が0に近いものをかけられて忘れるようにしているためですね。そして忘れた部分に+ sigmoid(i)*self._activation(j)として新しく活性化させたものを覚えさせるということをしています。うまい具合に特徴が保持されたり・更新されたりすることに数学ってすごいなとシミジミ思いました。

5.特徴保持をする内部状態

日本語で言うとなんとも言いづらいですけども、stateとかメモリーとかそんなニュアンスで理解していれば良いと思います。この内部状態が変化してくれるからこそ時系列データでうまく特徴を捉えられるようです。
内部状態の変化を追うにはそこから実際の予測した数字をシーケンスごとに並べてみると良いかもしれません。

ステップ毎の内部状態.py

Iter 1280, Minibatch Loss= 1.806859, Training Accuracy= 0.35938
y_ [ 0.  0.  0.  0.  0.  0.  0.  0.  1.  0.]
answers of n_steps 6 6 6 6 6 0 0 6 6 6 7 2 2 2 0 0 0 0 0 0 0 0 0 0 0 7 4 4
#右に行くほど最後のステップ
.
.
.
Iter 8960, Minibatch Loss= 0.827538, Training Accuracy= 0.75000
y_[ 0.  0.  0.  0.  0.  0.  1.  0.  0.  0.]
answers of n_steps 6 6 6 6 6 6 7 7 7 7 7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 6 6 6
.
.
.
Iter 99840, Minibatch Loss= 0.125606, Training Accuracy= 0.96094
y_[ 0.  0.  0.  0.  1.  0.  0.  0.  0.  0.]
answers of n_steps 6 6 6 6 6 6 6 6 6 6 9 8 9 9 9 9 0 0 0 0 0 0 4 4 4 4 4 4

こんな感じでシーケンスの最初の方はもう適当に答え6を出してるんですね。そして途中から何かを覚えたか忘れるかして、考え方を変えていきます。学習初期ではコロコロ考え方を変えていて最終シーケンスの答えもあっていませんが、学習終了頃にはしっかり最終シーケンスで正解の答えを言ってきてくれるようになります。ただし最初のシーケンスでは必ず6と言うようになってしまいました。　
ここでちょっと面白いなと思ったのは、この最初の適当な答え6が新規で学習されるたびに1やら3やらとこれまた適当な数字になったりするのです。実行するたびに学習してる感があった。

とまぁループ構造があってその中で細かくシグモイドが情報の取捨選択をうまくしてくれているからこそ内部情報に正しい特徴が保持されてLSTMがうまく機能しているんですね。

例えば音楽の話でいうと、Cコードが来たら次はGコードに行くみたいなギターの初心者の練習を曲のシーケンスとしてLSTMに与えると、見事にメジャーコードだけ弾いてくれるような学習をさせられるんじゃないでしょうか。 4分の4拍子で４回連続で出たCコードをsigmoidが毎回覚えると、内部状態にあるCコードの情報がかなり1に近くなり、活性化させるとGコードが出てくるといったイメージですね。多分。

6.ToBeContinued 色々実験

ちょっと時間なくて書ききれなかったので後からここら辺追記してみたいと思います。

画像を90度回転させたらどうなる

途中を黒塗りしたらどうなる

7.次回は強化学習で遊びたい

ちょっと急ぎ足で書いたので説明が荒いかもしれません。更新や追記は確実にします🙇
とりあえず個人的な解釈に基づいたLSTMの解説は以上です。　word2vecの解説をしていないのであれなのですが、RNN系の機械学習を理解しようとした時に自然言語などいきなり文字から入るとベクトルの扱いとかがわけわからなくて挫折してしまうことがあるんじゃないかと思います。　なので今回は誰でも馴染みのあるMNISTを使って説明いたしました。これが少しでも役に立つと嬉しいです。

もし次回があるとしたら強化学習あたりがいいなぁーなんて思ったり。　その頃にはもっと面白い何かが出て来ているかもしれませんが。

いいねが励みになるので、気に入ってくれたら嬉しいです⭐️🎉

自然言語系のデータでLSTM理解しようとすると難しいので、MNISTデータでLSTMの基礎を解説