Recurrent Neural Network (リカレントニューラルネットワーク)
時系列データなど連続値で相関がありそうなものに対して、入力を一つづつ処理しつつネットワーク内部で状態値を保持して、入力が全て終わった後に最終的な出力をしてくれるRNNさん。
実世界の時系列データだとノイズが入りすぎるし、Tensorflowのチュートリアルのような言語系だとイマイチ"時系列"としてのイメージが難しい。
そしてイマイチRNNCellクラスの仕様がつかめないので、諦めて実験的に簡単な自己フィードバックのモデルを作ってみます。
検証対象 : カオス力学
バタフライエフェクトで有名なカオスですが、一見ランダムに見えるんだけど実はある法則みたいなものがある事象を分析する上で役に立つやつです。
その中でも個人的に一番分かりやすい Logistic Map(ロジスティック写像)を例にお話をします。
離散型ロジスティック方程式
ある時点 $t$ における $x(t)$ の値が、一つ前の時点 $x(t-1)$ の値と固有のパラメータ $r$ から導き出せる下記の超簡単な式があります。
x_t = rx_{t-1}(1-x_{t-1})
もしくは一つ先の時点を予測したいのであれば、こうなります。
x_{t+1} = rx_t(1-x_t)
$x$は0 ≤ x ≤ 1 $r$は0 ≤ r ≤ 4
これのどこかカオスなのかというと、この数式は $r$ が 3.6あたりから$x$のとりえる値が莫大に増えます。
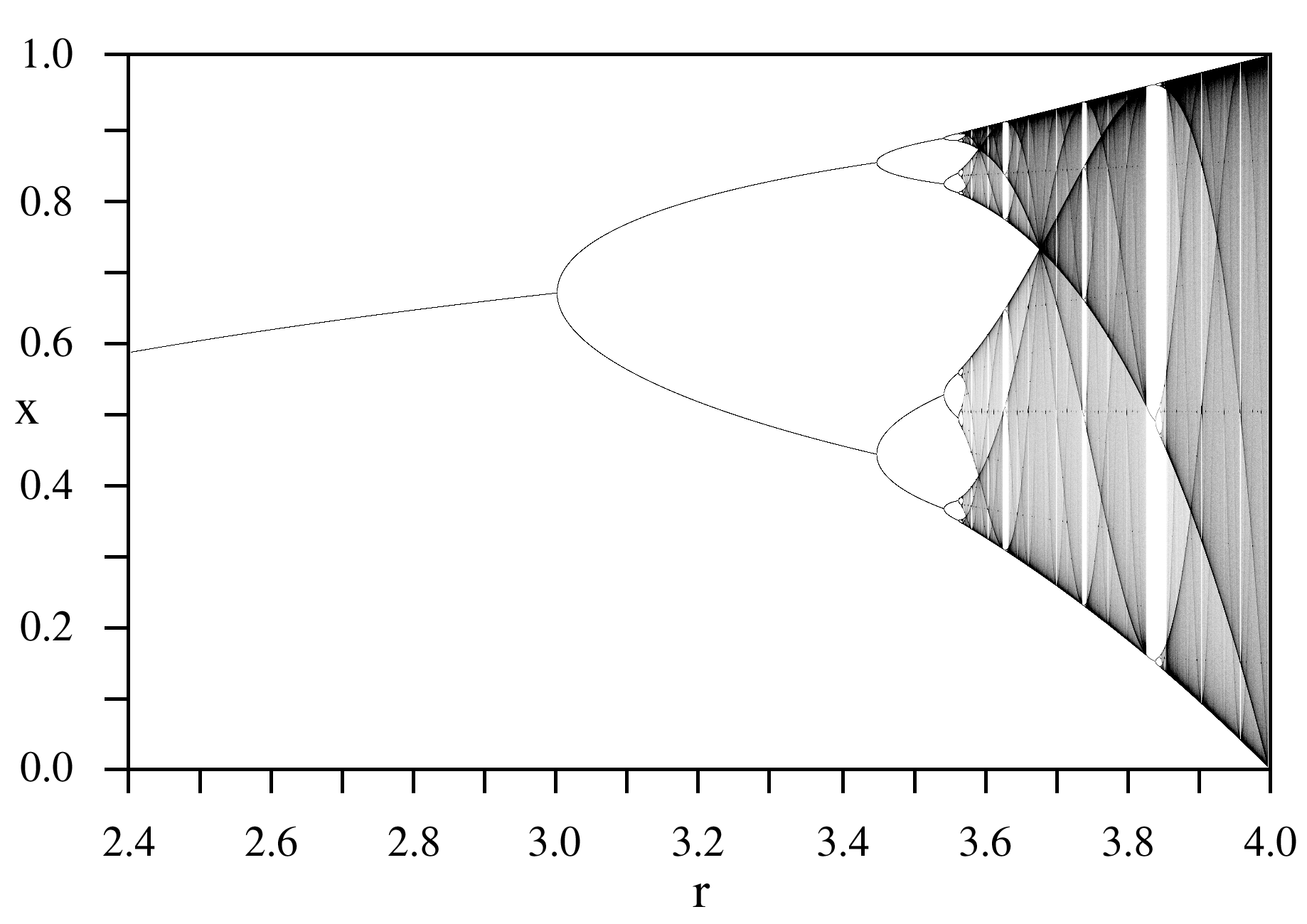
$x$を時系列データとしてみると、見事な乱数になってます。
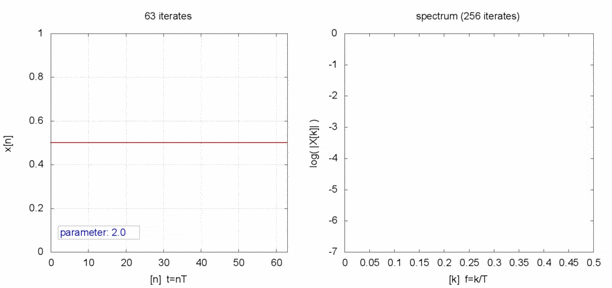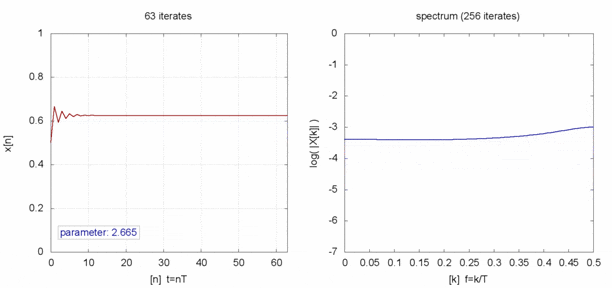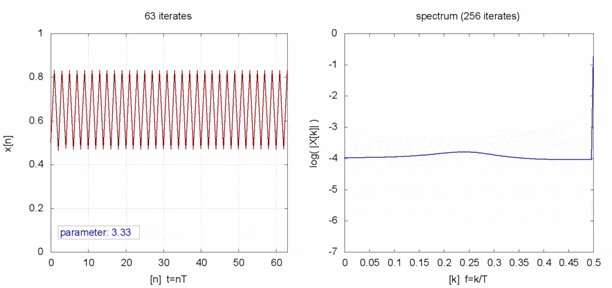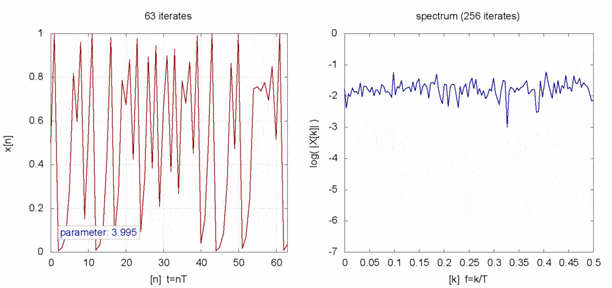
完全にランダムな値と時系列で比べると何も言われなければ違いが分からなそうです。
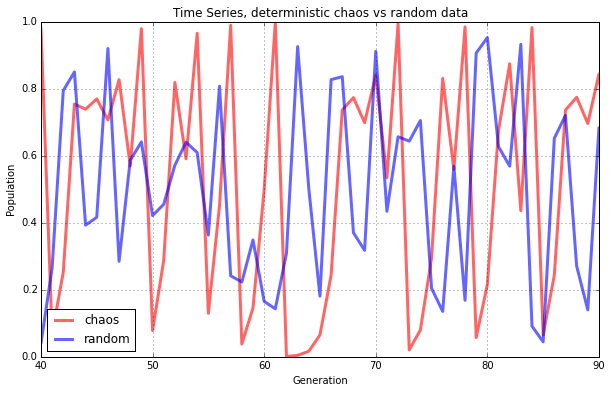
カオスが素晴らしいのはここで、$x_t$ と $x_{t+1}$を散布図にしていくと、なにやらカッコいい形(フラクタル)がでてきます。さきほどのランダムな値と比べても違いは明らかですね。
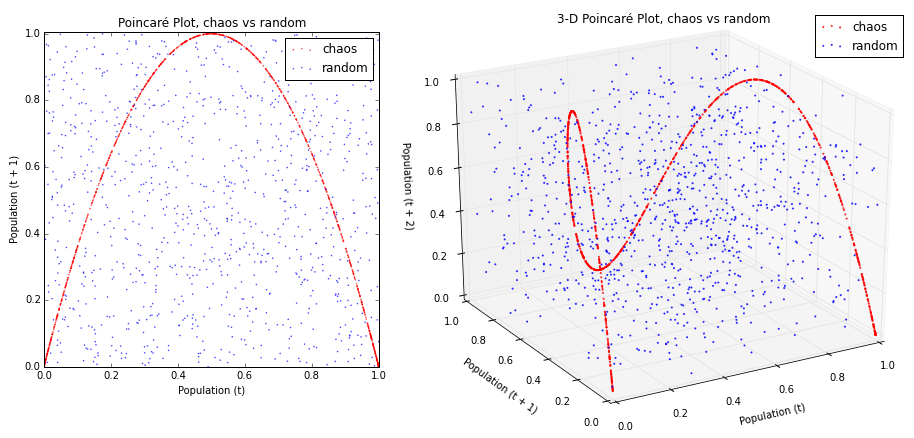
$r$を起点にしているようです。あー美しい。
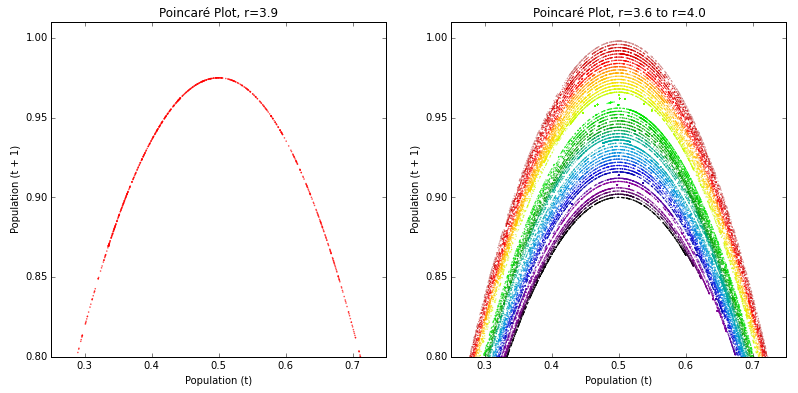
カオス力学の短期予測
さてさてそんな美しいカオスですが、ランダムに見えても法則にしたがっているなら簡単に予測できそうですよね。ところがどっこい。カオスがカオスたる所以なのですが、初期値やパラメーターがほんの僅か違うだけでまったく違う値になってしまうため、連続したデータの予測が難しいのです。
適当に比べてみましょう。
def logistic(r, t_first, num_steps):
array = []
for i in range(num_steps):
if "t" not in locals():
t = t_first
else:
t = tt
tt = r*t*(1-t)
array.append(tt)
return array
initial = 0.5
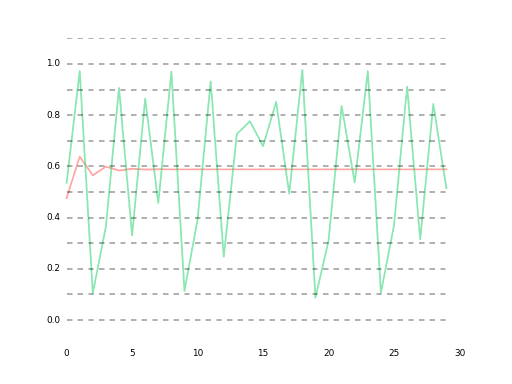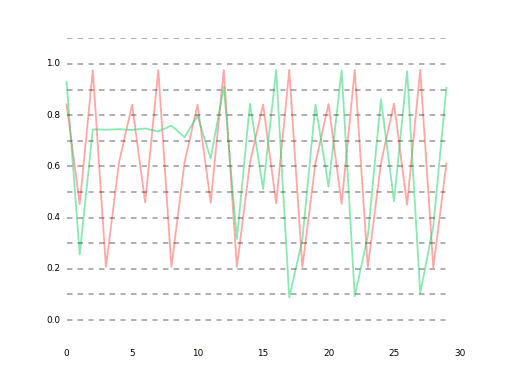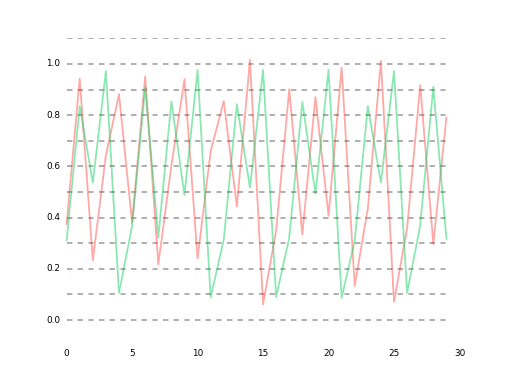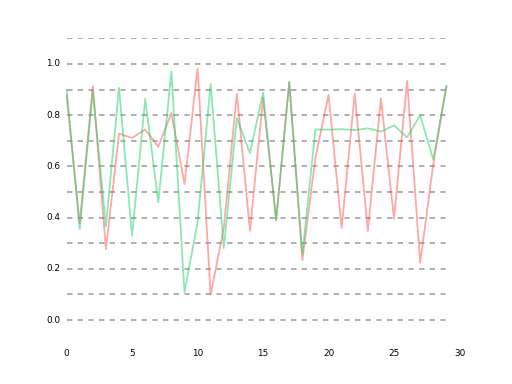
data1 = logistic(3.91, initial, 100)
data2 = logistic(3.9100000000001, initial, 100)
data3 = logistic(3.91, initial+0.0000001, 100)
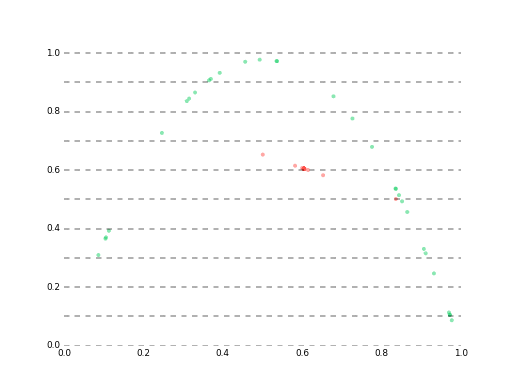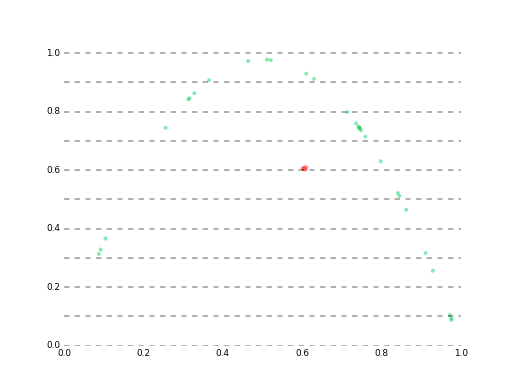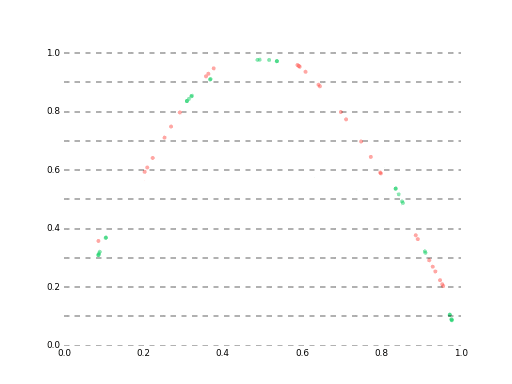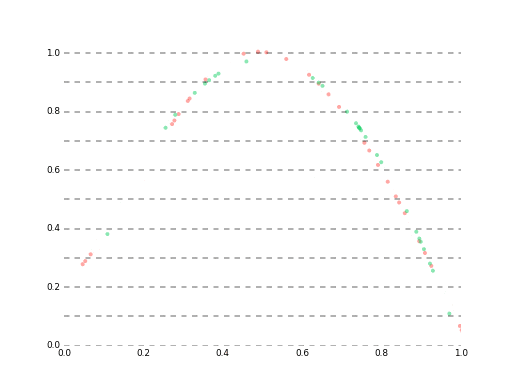
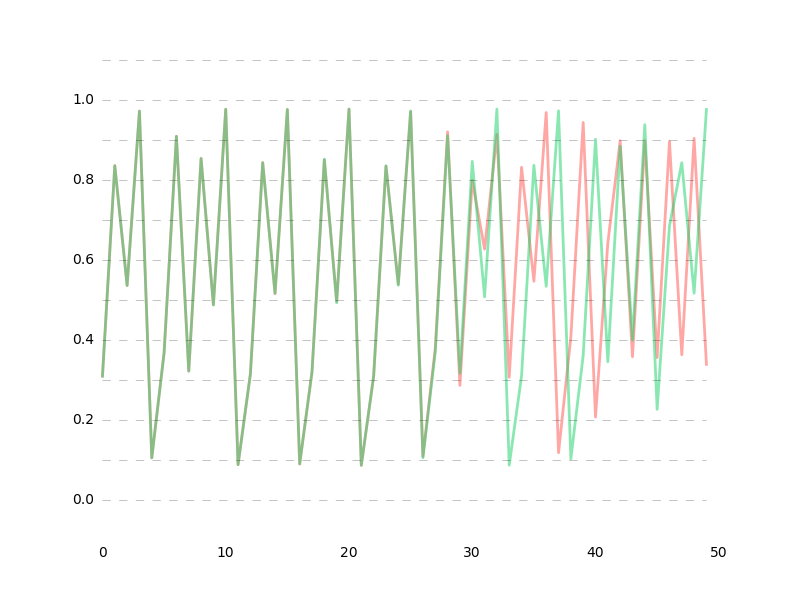
※緑がdata1
data1 vs data2
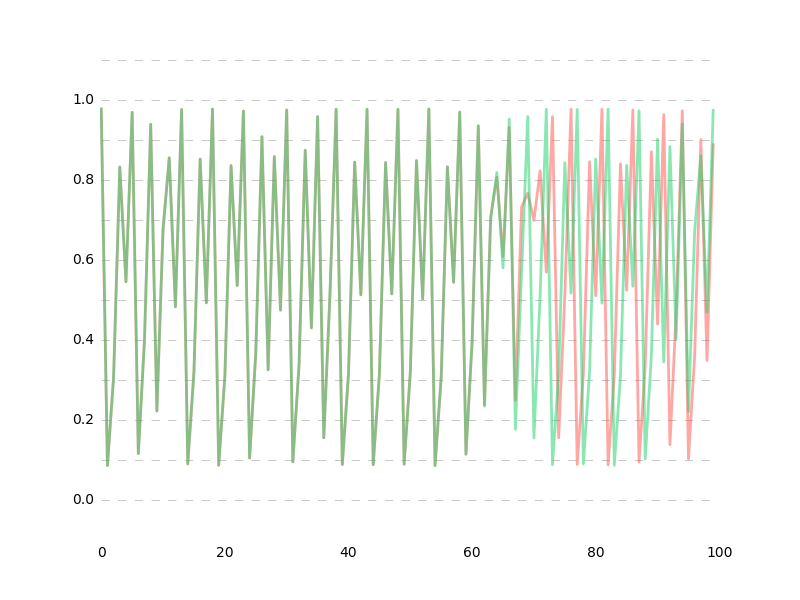
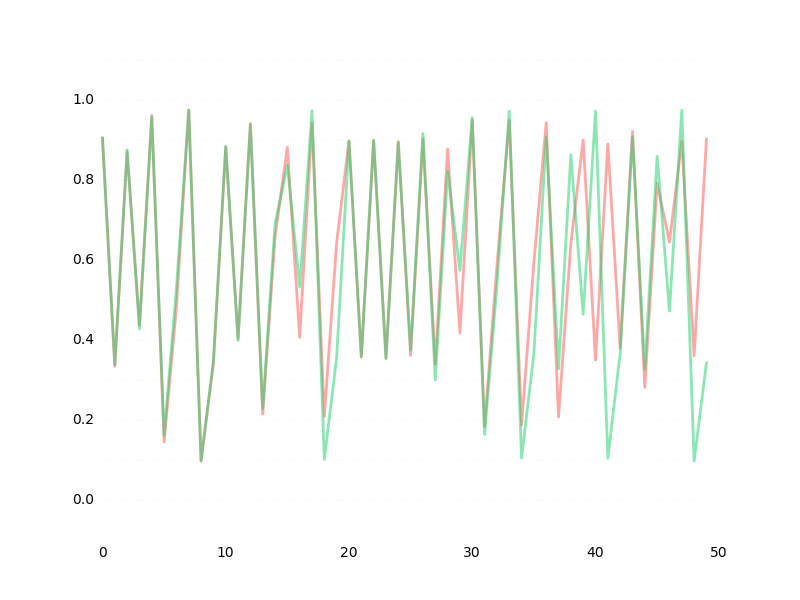
data1 vs data3
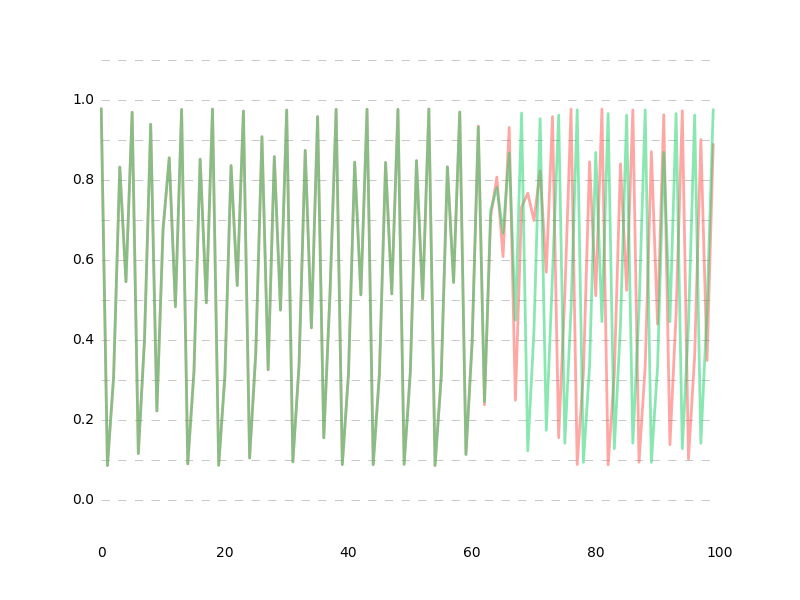
推定値の誤差が1e-10%以下の超超高精度だったとしても、60データ先ではもう予測が困難になってしまいます。
逆に言うならば$r$を探すような回帰を行えば、短期の予測はある程度できるんじゃなかろうか。
import os, sys
import numpy as np
import tensorflow as tf
num_steps = 1 # Number of inputs. logistic map only needs a current input
batch_size = 100
epoch_size = 10000
initial = 0.5 # 0 <= x <= 1: to generate data
L = 0.01 # learing rate
PRE_STEPS = 30 # Number of predictions. how far do you want to predict?
N_HIDDEN = 30 # Hidden nodes
'''
generate data
'''
def logistic(r, t_first, num_steps):
array = []
for i in range(num_steps):
if "t" not in locals():
t = t_first
else:
t = tt
tt = r*t*(1-t)
array.append(tt)
return array
def logmap_iterator(raw_data, batch_size, num_steps, prediction_steps):
raw_data = np.array(raw_data)
data_len = len(raw_data)
batch_len = data_len // batch_size
data = np.zeros([batch_size, batch_len])
for i in range(batch_size):
data[i] = raw_data[batch_len * i:batch_len * (i + 1)]
epoch_size = (batch_len - 1) // num_steps
if epoch_size == 0:
raise ValueError("epoch_size == 0, decrease batch_size or num_steps")
for i in range(epoch_size):
x = data[:, i*num_steps:(i+1)*num_steps]
y = data[:, (i+1)*num_steps:(i+1)*num_steps+(prediction_steps)]
yield(x, y)
raw_data = logistic(3.91, initial, num_steps*batch_size*epoch_size)
'''
mini-RNN Model
'''
x = tf.placeholder("float", [None, num_steps])
y = tf.placeholder("float", [None, PRE_STEPS])
weights = {
'hidden': tf.get_variable("hidden", shape=[1, N_HIDDEN], initializer=tf.truncated_normal_initializer(stddev=0.1)),
'out': tf.get_variable("out", shape=[N_HIDDEN, 1], initializer=tf.truncated_normal_initializer(stddev=0.1))
}
biases = {
'hidden': tf.get_variable("b_hidden", shape=[N_HIDDEN], initializer=tf.truncated_normal_initializer(stddev=0.1)),
'out': tf.get_variable("b_out", shape=[1], initializer=tf.truncated_normal_initializer(stddev=0.1))
}
def simple_reg(x, _weights, _biases, K = 1.0):
with tf.variable_scope("weight"):
h1 = tf.matmul(x, _weights['hidden']) + _biases['hidden']
h1 = tf.nn.dropout(tf.nn.sigmoid(h1), K)
o1 = tf.matmul(h1, _weights['out']) + _biases['out']
with tf.variable_scope("weight", reuse=True):
h2 = tf.matmul(o1, _weights['hidden']) + _biases['hidden']
h2 = tf.nn.dropout(tf.nn.sigmoid(h2), K)
o2 = tf.matmul(h2, _weights['out']) + _biases['out']
o = tf.concat(1, [o1, o2])
def more_step(predicted_value, o):
with tf.variable_scope("weight", reuse=True):
h = tf.matmul(predicted_value, _weights['hidden']) + _biases['hidden']
h = tf.nn.dropout(tf.nn.sigmoid(h), K)
o_v = tf.matmul(h, _weights['out']) + _biases['out']
o = tf.concat(1, [o, o_v])
return o, o_v
for i in range(PRE_STEPS-2):
if "o_v" not in locals():
o, o_v = more_step(o2, o)
else:
print o_v
o, o_v = more_step(o_v, o)
return o, o1
o, o1 = simple_reg(x, weights, biases)
z = tf.split(1, PRE_STEPS, y)
z = z[0]
cost = tf.reduce_sum(tf.square(o1 - z))
optimizer = tf.train.AdamOptimizer(L).minimize(cost)
init = tf.initialize_all_variables()
with tf.Session() as sess:
saver = tf.train.Saver()
sess.run(init)
for step in range(10):
gen = logmap_iterator(raw_data, batch_size, num_steps, PRE_STEPS)
for i in range(epoch_size-batch_size):
s, a = gen.next()
training = sess.run([optimizer, o, cost], {x:s, y:a})
if i % 100 == 0:
print "i", i, "cost", training[2]
print "initial input", s[0][:5]
print "pred", training[1][0][:5]
print "answ", a[0][:5]
if i % 2000 == 2000:
L = L/2
save_path = saver.save(sess, "dynamic_model.ckpt")
モデルの形としてはこんな感じですかね。 久しぶりにイラストレーター触った...
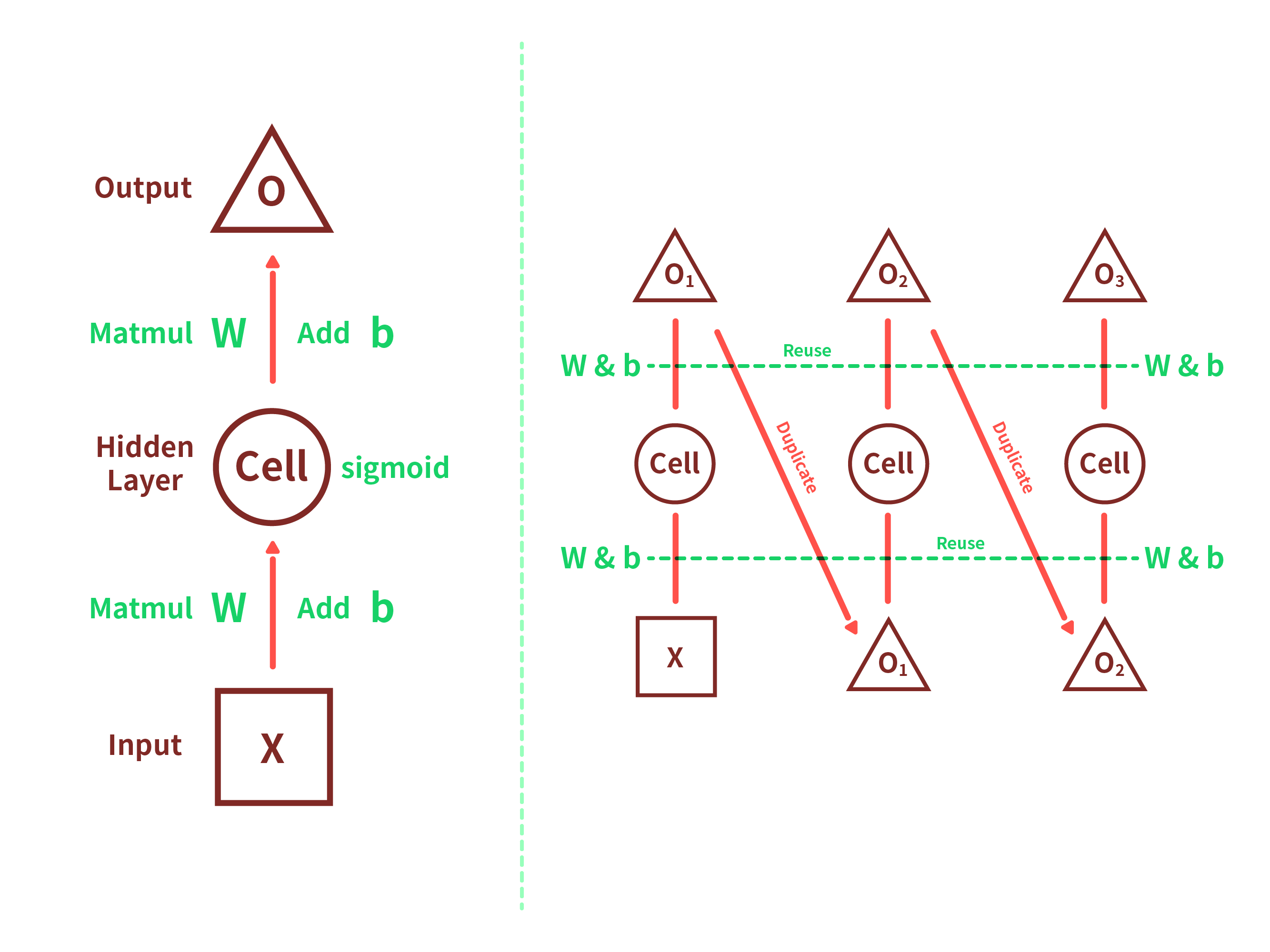
隠れ層の数は適当で、$sigmoid$を使っている理由は単純に出力がbetween 0 and 1で収まるからです。
入力は1つだけの数値になっていますが、これは$x_{t+1}$を求めるために$x_t$以外意味をなさないためです。そのためネットワーク内部の状態値の共有とかはありません。
(本当は入力を増やすとlossがうまく減少しなかったのは内緒)
これを正式にRNNとは呼べないのでしょうが、まぁ一応Feedloopなので。
(本当は連続した$\in x_n$から $r$ を推定して $x_{n+1}$を出力、その $x_{n+1}$ をまた入力に加えて$x_{n+...}$ としたほうが精度もあがるんじゃないかなとも思うけど、TensorflowのRNNCellがイマイチうまく使えなかった。)
とりあえず個人的には満足する結果が出ました。
最終的にはlossが大体1e-5あたりに落ち着いて、ベストな予測でこんな感じになります。
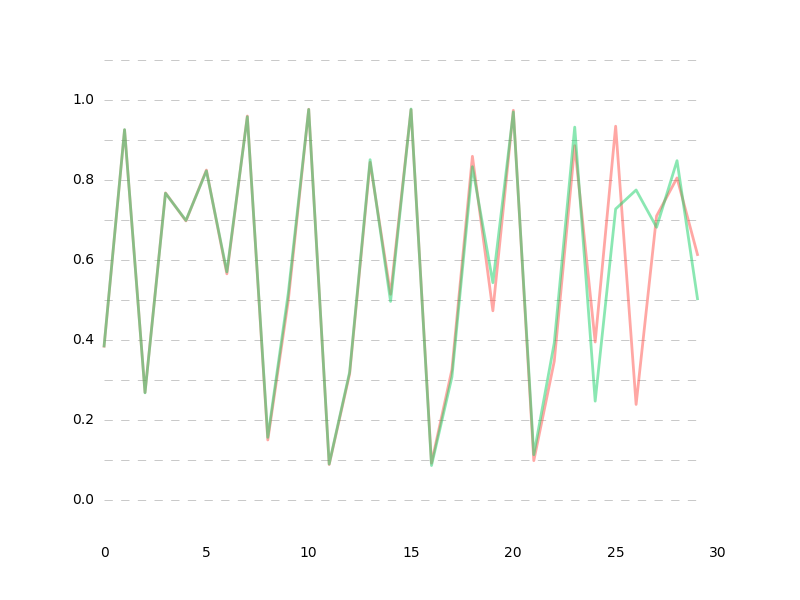
※一度アップした記事なんですが、高精度なモデルを模索してる間だけ非公開にしてました。
高精度なモデルはイマイチ発見できなかったので、単純にlossを1e-6くらいまで下げ続けた結果は35ステップ先まであらかた予測できる(というか$r$ができるだけ近似した)状態になりました。
これがローレンツなど他のカオス系方程式に使えるかはまだ試してないのでわかりません。