どうも、データセットの用意でバイナリーとの戦いを5時間繰り広げたあげく、記事に1日かかりました。丁寧に記事書くって大変ですね。うふふっ☆
前回: 特にプログラマーでもデータサイエンティストでもないけど、Tensorflowを1ヶ月触ったので超分かりやすく解説
に続き、MNISTのエキスパート編を解説しようと思ったのですが、せっかくなので数字ではなくひらがなデータセット計71文字を識別していくなかで**"畳み込みニューラルネットワーク"の解説をしたいと思います。 英語ではConvolutional Neural Networkなので以下CNN**と呼びます
コードはほぼTensorflowのチュートリアルエキスパート編のものですので、そちらを見てからだとよりわかりやすいかと。
1: データセット
産総研(AIST)の公開しているETL手書き文字データベースからいただきました。(旧:電総研のためETL(ElectroTechnical Laboratory))
あえて名付けるならMNISTならぬMAIST (Mixed Advanced Industrial Science and Technology) データセット

実データは127x128で大きめなのですが、Tensorflowのチュートリアルに合わせるため28x28に縮小しています。
2: 大事なのは特徴と次元削減方法や!
さて、エキスパートのチュートリアルですが。
いきなり畳み込みとかプーリングとか新しい単語言われても、本当にチンプンカンプンじゃないですか。
もう少し前回とつながるように話をしましょ?ね?
ビギナーチュートリアルでは重みW:[784, 10]を行列演算して画像を10次元にまで減らして答え合わせをしていました。 この重みはピクセル単位で「ここが0の可能性は0.3%、1の可能性は21.1%...ほにゃほにゃ」と言っているやつです。
しかしながら0なんだけどかなり下に寄ってるちっちゃい0とか出てきた場合、この重みで次元削減された画像は結構な確率で「答えは6です!」と言ってくるでしょう。少なくとも"0"の答えが返ってくる可能性がかなり下がります。
なぜなら重みWが持つ真ん中あたりのピクセルの評価は「0の可能性は-0.23017341」などとなっているからです。 人間なら「丸いから0」と即判断できますよね。 この**"丸いから"というのが実は大事な特徴**だったりします。
もう少し詳しく述べるなら、画像なので対象のピクセルと周辺のピクセルとの関係性があるはずなのに、ベクトル変形して次元削減をするとその関係性(特徴)が失われてしまうのではないでしょうか。
前回の"1"の画像だったベクトルグラフを改めて見てみると、ここから周辺のピクセルとの関係性が全くわかりません。
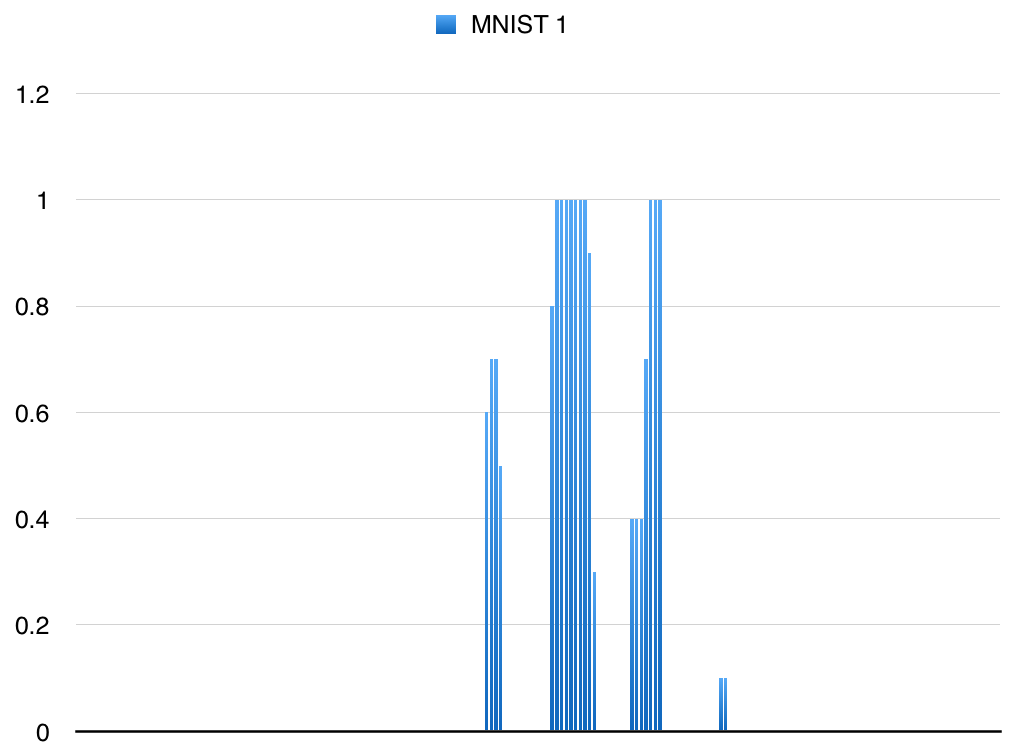
この784次元ベクトルから10次元ベクトルまで減らすということは、かなり大雑把に答えを出すようなものです。
つまり次元削減の過程で**"丸い"という特徴が失われた**と言えます。
ビギナーチュートリアルのモデルだと、手書きひらがなは認識できない。
Tensorflowのチュートリアルだと、正答率がビギナーの91%の精度からエキスパートの99.2%精度なので一般人にとっては「ふーん。」で終わってしまいます。
(実はこの差が超すごいというのはサイエンス畑の人には明白のようです。ブレイキングバッドでも言われてました。)
なので今回のひらがなMAISTは2つのチュートリアルを比べる上でとても良いベンチマークになりました。
train_step = tf.train.GradientDescentOptimizer(1e-4).minimize(cross_entropy)
# 学習回数が多いと発散してしまうので、学習レートを1e-4に変更
for i in range(10000):
batch = random_index(50) #load 50 examples
train_step.run(feed_dict={x: train_image[batch], y_: train_label[batch]})
print accuracy.eval(feed_dict={x: test_image, y_: test_label})
> simple_maist 10000 steps accuracy 0.287933
> simple_maist 50000 steps accuracy 0.408602
> simple_maist 100000 steps accuracy 0.456392
なんということでしょう...前回使ったビギナーチュートリアルのコードでは10000回学習させても**28.79%**にしかなりません。 50000回学習させても40.86%、100000回学習させても45.63%。
次元削減によって特徴が失われることがいかに恐ろしいかよく分かります。
頭の良い人たちはきっとこう思ったのでしょう。"答え出すには次元削減が必要だ。でも特徴を残したい。"
そこでエキスパート編のモデル: CNNには
特徴検出のConvolution: 畳み込み
特徴強調のActivation:活性化
次元削減のPooling: プーリング
全結合のConnected Layer(Hidden): 隠れ層
が登場します。
3: Convolution: 畳み込み
さて順番に中身を見てみましょう。
まずはコードの解説
x_image = tf.reshape(x, [-1,28,28,1])
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
W_conv1 = weight_variable([5, 5, 1, 32])
Conv1 = conv2d(x_image, W_conv1)
CNNでは画像をベクトルとして処理せずに、画像として特徴の意味を保てる28x28のマトリックスで処理していきます。Tensorflow的に言うとx_image = tf.reshape(x, [-1,28,28,1])でベクトルだったものを元の画像のshapeに戻してあげてるんですね。
そして特徴検出の畳み込みです。 "畳み込む"という単語が意味不明ですし、前回でも若干書きましたがこれは"重み"変数でもあるのでフィルターと解釈しちゃいましょう。
W_conv1の中にRank 4のVariable変数/Tensor[5, 5, 1, 32]が入ります。 このTensorW_conv1:のshapeですが、意味は[width, height, input, filters]となっていて各画像に対して5x5のサイズのフィルターを適用していきます。
前回は初期化がtf.zeros()でしたが、今回の初期化はtf.truncated_normal()で様はランダムな数値が入ります。
うーん、わからん!
このフィルター達ですがconv2d(x_image, W_conv1)でもちろん画像に適用されます。適用された画像:(ふ)はこちら。はい、どん!

なんか余計分かりづらくなりましたね。 それもそのはずで、最初の段階ではこちらのフィルター達も最適化されていないからです。
では学習完了後のフィルターとその適用画像をみてみましょう。
学習完了後のフィルター:なんとなく線っぽくなってる気がするようなしないような。

学習完了後の適用画像:(ず): なんか立体感がこうクワっ!と増したような気がします

ちょっと人間には解釈が難しいですね...
4: Activation: 活性化
意味のある特徴もあれば、意味のない空白の白いピクセル達もいますよね。
次元削減するまえにできるだけ特徴のみ強調しておきたいです。
そこで活性化関数 Reluが登場します。 (バイアスはもはや( ^o^)デフォ...)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(Conv + b_conv1)
バイアスb_conv1はtf.constant()で指定した数値で満たされたTensorになっています。今回は0.1ですね。
活性化も分かりやすく、先ほどのConvをtf.nn.reluに渡しているだけです。
※2016/5/16補足
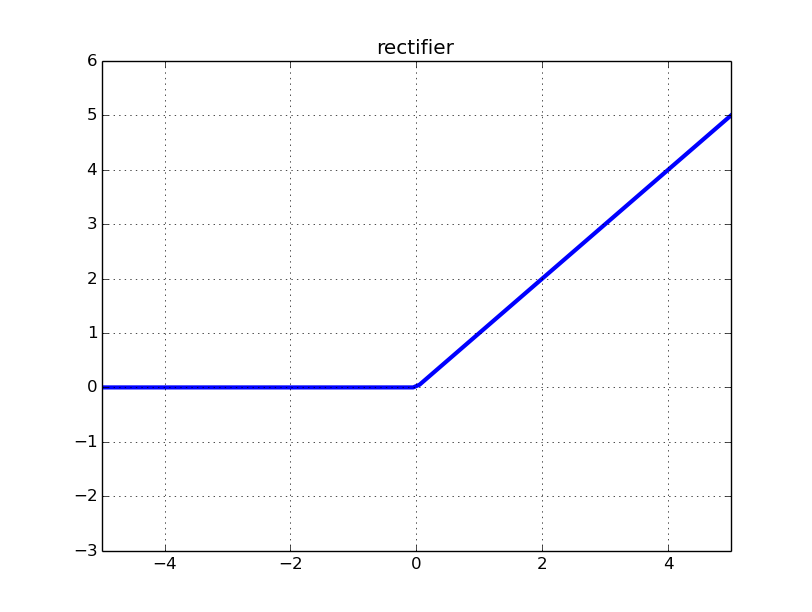
Relu関数ですが、Rectified Linear Unitなので簡単に言うと補正付きの直線関数に持っているもの渡します。Reluの場合は入力が0.以下、つまりマイナスの数値であると全て0.に補正されます。
図を見ると一目で理解できます。こんな感じです。
実はeluやらLeakyReluなど他にもあります。
直線ではないものでsigmoidやtanh関数などもあります。
今回のMAISTで言うと画像の色が濃い部分は数値が低くなっており、コンピューター的には特徴として検出されていないので、あまり考慮したくない状態(数値)になっています。
そこで活性化関数を通して無用な奴らを全て0.にします。要は足切りですね。リストラ怖い。
-> x
[ 1.43326855 -10.14613152 2.10967159 6.07900429 -3.25419664
-1.93730605 -8.57098293 10.21759605 1.16319525 2.90590048]
-> Relu(x)
[ 1.43326855 0. 2.10967159 6.07900429 0.
0. 0. 10.21759605 1.16319525 2.90590048]
何が起きてるのか画像:(ず)にするとさらに分かりやすいです。

特徴が強く残っている(白い)部分以外が真っ黒になりました。
わぁー綺麗に特徴だけ残ってるぅ〜!分かりやすい〜!といった感じでしょうか。
5: Pooling: プーリング
畳み込まれて活性化された画像はうまい具合に特徴抽出されているので、次元削減のお時間です。
プーリングの場合はどちらかと言うと圧縮に近いかもしれません。
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
h_pool1 = max_pool_2x2(h_conv1)
プーリングはちょっと分かりづらいのですが、 ksize=[1, 2, 2, 1]が2x2のpixel枠を作り、strides=[1, 2, 2, 1]で 2x2のpixel移動をしていきます。 tf.nn.max_poolの場合はksizeで指定されたサイズの枠の中で一番大きい値を圧縮後の1pixelとして捉えます。
この図が分かりやすいです。

図の場合はピンクで6,緑で8,黄色で3,青で4が値として圧縮後の画像として生成されています。
tf.nn.max_pool以外にも枠内の平均値をとるtf.nn.avg_poolもあります。
特徴メインに圧縮というより、そのまま圧縮したい場合や空白の位置関係とかも意味がある場合にはtf.nn.avg_poolの方がいいのかもしれませんね。
さて肝心のMAISTの場合で見てみましょう。
先ほどの活性化された画像:(ず)はプーリングでこのような14x14の画像になります。

人間には視認で判断できなくなりましたが、特徴だけうまく残りながら画像が小さくなったのではないでしょうか。
このあとにもう一回同じ処理を一通りして、画像は最終的に[batch_num, 7, 7, 64]なります。
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
よくよく考えると画像の次元は減ったけども、対象の画像は64の特徴に増えてますね。
ここら辺はフィルターの数の設定次第ですし、フィルターの数増やすと計算処理がどんどん重くなるのでパソコンのスペックやデータ数などを考慮しながら調整すればいいようです。
フィルターを1枚にして[batch_num, 7, 7, 1]だとしても一応学習はできます。
もちろん精度は落ちますが、それでもビギナーのモデルよりは精度が良いです。2倍くらい。
6: Hidden layer: 隠れ層
答え合わせが近づいてきました。
隠れ層は行列演算をしているだけなので、そこまで難しくはありません。
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
W_fc1 = weight_variable([3136, 1024]) #[7*7*64, 1024] 3136はTensorのsize, 1024は適当。 業界的に大抵は1024もしくは1024*nの倍数らしい。
b_fc1 = bias_variable([1024])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
# Dropout
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
特徴いっぱい☆ウハウハTensor h_pool2: [batch_num, 7, 7, 64]
こいつをまずはtf.reshape(h_pool2, [-1, 7*7*64]) でベクトルに戻します。
あとは重みW_fc1: [3136, 1024]と行列演算してバイアスを付け足して、活性化しているだけです。
なぜ一気に答えの数まで行列演算しないかというと、できるだけ特徴を残しながら答え合わせに近づきたいというのと、学習データだけに適応してしまう過学習を回避するためのようです。
次元を潰しすぎた場合にうまく答えが出せなくなってしまう理由/隠れ層の役目は
@KojiOhkiさん訳のQiita: ニューラルネットワーク、多様体、トポロジーの**"トポロジーと分類"**を参照してください。
適当に言うと別クラスのデータ同士の特徴相関が強いor被ったりしている場合や、次元削減でうまく切り分けられない場合、または決定変数がどこか違う場所にある場合などは回帰分析って難しいよってことなのかと。
顔だけからおっぱいのサイズを判断できないのは、これに当てはまるかもしれません。 逆に声からおっぱいのサイズが分かったりするのかもしれない。 だからこそ試して楽しいDeep Learningであります。
過学習については h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob) の部分ですが学習結果のあとに後述します
7: 学習結果
今回のネットワークだと10000stepsで**87.15%**精度になりました。
ビギナーのモデルでは28.79%だったので、CNN様様と言ったところでしょうか。
simple_maist 10000 steps accuracy 0.287933
now MAIST-CNN...
i 0, training accuracy 0 cross_entropy 1200.03
i 100, training accuracy 0.02 cross_entropy 212.827
i 200, training accuracy 0.14 cross_entropy 202.12
i 300, training accuracy 0.02 cross_entropy 199.995
i 400, training accuracy 0.14 cross_entropy 194.412
i 500, training accuracy 0.1 cross_entropy 192.861
i 600, training accuracy 0.14 cross_entropy 189.393
i 700, training accuracy 0.16 cross_entropy 174.141
i 800, training accuracy 0.24 cross_entropy 168.601
i 900, training accuracy 0.3 cross_entropy 152.631
...
i 9000, training accuracy 0.96 cross_entropy 8.65753
i 9100, training accuracy 0.96 cross_entropy 11.4614
i 9200, training accuracy 0.98 cross_entropy 6.01312
i 9300, training accuracy 0.96 cross_entropy 10.5093
i 9400, training accuracy 0.98 cross_entropy 6.48081
i 9500, training accuracy 0.98 cross_entropy 6.87556
i 9600, training accuracy 1 cross_entropy 7.201
i 9700, training accuracy 0.98 cross_entropy 11.6251
i 9800, training accuracy 0.98 cross_entropy 6.81862
i 9900, training accuracy 1 cross_entropy 4.18039
test accuracy 0.871565
今のDeep Learning業界はいかにうまく特徴を見つけて、次元削減をするか?を極めることで結構有名になれるのかもしれません。

8: (Fine Tuning) 学習発散と過学習防止
頭良かったCNNモデルが何も分からなくなってしまう学習発散
今回のひらがなMAISTですがエキスパートチュートリアルのように学習回数を20000回にすると、15000あたりから、学習データに対する正答率の精度がいっきにがくっと2%くらいまで落ちます。
なぜいきなり発散するのか、詳しいメカニズムを把握していないのですが、学習が進んだら学習レートを下げていかないと、おそらくCross Entropyが完全な0かマイナスに達するのか何かになってGradientが爆発して起きるのかなと適当に予想してます。
そのための防止策はこんな感じでしょうか。
L = 1e-3 #学習レート
train_step = tf.train.AdamOptimizer(L).minimize(cross_entropy)
for i in range(20000):
batch = random_index(50)
if i == 1000:
L = 1e-4
if i == 5000:
L = 1e-5
if i == 10000:
L = 1e-6
...
i 19800, training accuracy 1 cross_entropy 6.3539e-05
i 19900, training accuracy 1 cross_entropy 0.00904318
test accuracy 0.919952
学習を20000回すると精度91.99%。まぁこんなものですかね。
学習100回毎くらいのcross_entropyを見て、適当な段階をつけただけです。
ほんとうはこの学習レートを自動で調整してくれるようにもできるのですが、意外と超精度を目指すなら手作業でもいいのかもしれない。
評価用データでのスコアが悪いんだけどぉ? (`・ω・´)っ[過学習防止]
隠れ層にのっていたコード h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)ですが
過学習防止で結構重要みたいです。
学習発散防止と合わせてさらに設定するとこうなりました。
for i in range(20000):
batch = random_index(50)
# tune the learning rate
if i == 1000:
L = 1e-4
if i == 3000:
L = 1e-5
if i == 7000:
L = 1e-6
if i == 10000:
L = 1e-7
if i == 14000:
L = 1e-8
if i == 19000:
L = 1e-9
# tune the dropout
if i < 3000:
train_step.run(feed_dict={x: train_image[batch], y_: train_label[batch], keep_prob: 1})
elif i >= 3000 and i < 10000:
train_step.run(feed_dict={x: train_image[batch], y_: train_label[batch], keep_prob: 0.3})
elif i >= 10000 and i < 15000:
train_step.run(feed_dict={x: train_image[batch], y_: train_label[batch], keep_prob: 0.1})
elif i >= 15000 and i < 19000:
train_step.run(feed_dict={x: train_image[batch], y_: train_label[batch], keep_prob: 0.05})
else:
train_step.run(feed_dict={x: train_image[batch], y_: train_label[batch], keep_prob: 0.8})
...
i 19900, training accuracy 1 cross_entropy 0.0656946
test accuracy 0.950418
評価データで95.04%
学習が発散しない限り学習回数を増やしまくるのも手ではありますが、はじめに一気に学ばせてから最後の直前までどんどん忘れさせる形式にしてみたら、ここまでの精度にできました。
最初の 87.15% から 95.04% なのでなかなか良い調整できたのではないでしょうか。
モデルが機能しているならば、そこからは職人技なのかもしれません。
計算処理が多い場合は時間がかかるので、評価用データの精度もできれば学習1000step毎位で見てあげた方が過学習検知をすぐできて良いです。 意外と作ってみたモデルの学習精度が80%いったのに、評価用データでは20%とかあったりします。 分類するクラスの数にも依存しますけども。
まとめと次回...?
CNNで学習がうまくいかない場合は可視化をすることで結構構造上の問題点が把握しやすくなります。
可視化はsess.runでTensorの中身を受け取り、matplotlibとか使えば簡単にできますので。
MNISTの可視化、詳しい処理を見たい方は下記のサイトがおすすめです。
なんとJavaScriptでディープラーニング実装するという狂気
ConvNetJS - http://cs.stanford.edu/people/karpathy/convnetjs/demo/mnist.html
次回はできれば検索予測などの基盤になっているLSTMのさらに基礎となるword2vecを解説したいのですがいつになることやら。 word2vecはWeb系(もしくは全)企業がデータ分析に応用しやすそうな楽しいアルゴリズムです。
ただし高度なモデルや大量のデータになればなるほど、個人が手持ちのパソコンでやるには時間がかかりすぎて限界になってくるのをヒシヒシと感じております。
画像認識モデル最強のGoogle Inceptionとかも解説したいのですが...超金欠な私にクラウド環境使ったDistributed Tensorflowは難しいかなぁー!
そんなこんなで余談は以上です。
ストック、ツイート、いいね、はてぶ、コメントなどなど、全て励みになるのでもしよければお願いします〜。
バズり方が前回超えたら次回やろう。うん、そうしよう。
※2016.12.12追記
Advent CalendarでLSTMの解説を書きました。
>これを理解できれば自然言語処理もできちゃう? MNISTでRNN(LSTM)を触りながら解説
