巡回セールスマン問題をいろんな近似解法で解く（その1: 総当たり法とグリーディ法）

はじめに

巡回セールスマン問題（traveling salesman problem, TSP）とは、ある都市から出発してすべての都市をちょうど1度ずつ訪れたのち、もとの都市に戻るルート（巡回路）のうち、総距離が最小となるものを求める問題です。組合せ最適化という分野で古くから研究されており、かつ同分野の代表的な問題でもあるため、一度はどこかで耳にしたことがあるかもしれません。

一見、コンピュータで簡単に解けそうな問題のように思えますし、実際都市の数が少ないうちは結構いけるのですが、都市の数が増えると解の候補が爆発的に増え、途端に解くのが難しくなることが知られています。

本記事では、TSPをいろいろな手法を用いて解き、どの程度の時間と精度で解が得られるかを見ていきたいと思います。

他の記事 （2022/05/30 追記）

他の記事へのリンクを以下に記載しましたので、ご興味ある方はぜひ読んでみてください。

• その2: 局所探索法と2-opt近傍
• その3: ランダム化最近近傍法とGRASP法
• その4: 反復局所探索法
• その5: 焼きなまし法
• その6: さまざまな近傍

総当たり法で解く

まずはシンプルに総当たり法で解いてみます。

以下に示すように、$n$都市のTSPについて一つ一つの都市に1から番号を振っていくとすると、その巡回路は1から$n$までの整数の並び替え（順列）で表現できます。

$n$個の要素の並び替えなので、総当たり法で解こうとすると$n!$通りの組み合わせを虱潰しに調べる必要がありますが、TSPの場合は円順列かつ裏返しの解は省略できる¹ため、厳密には数珠順列となり$\frac{(n-1)!}{2}$通りとなります。

このことを$O(n!)$の計算量と呼んだりしますが、詳しい説明は省きます。大体$n!$の定数倍くらいの計算ステップ（四則演算や条件判定の一つ一つ）が必要だよ、という程度の意味だと理解してもらえれば良いと思います。

それではさっそく、10都市の問題を解いた例を以下に示します。

10都市TSP

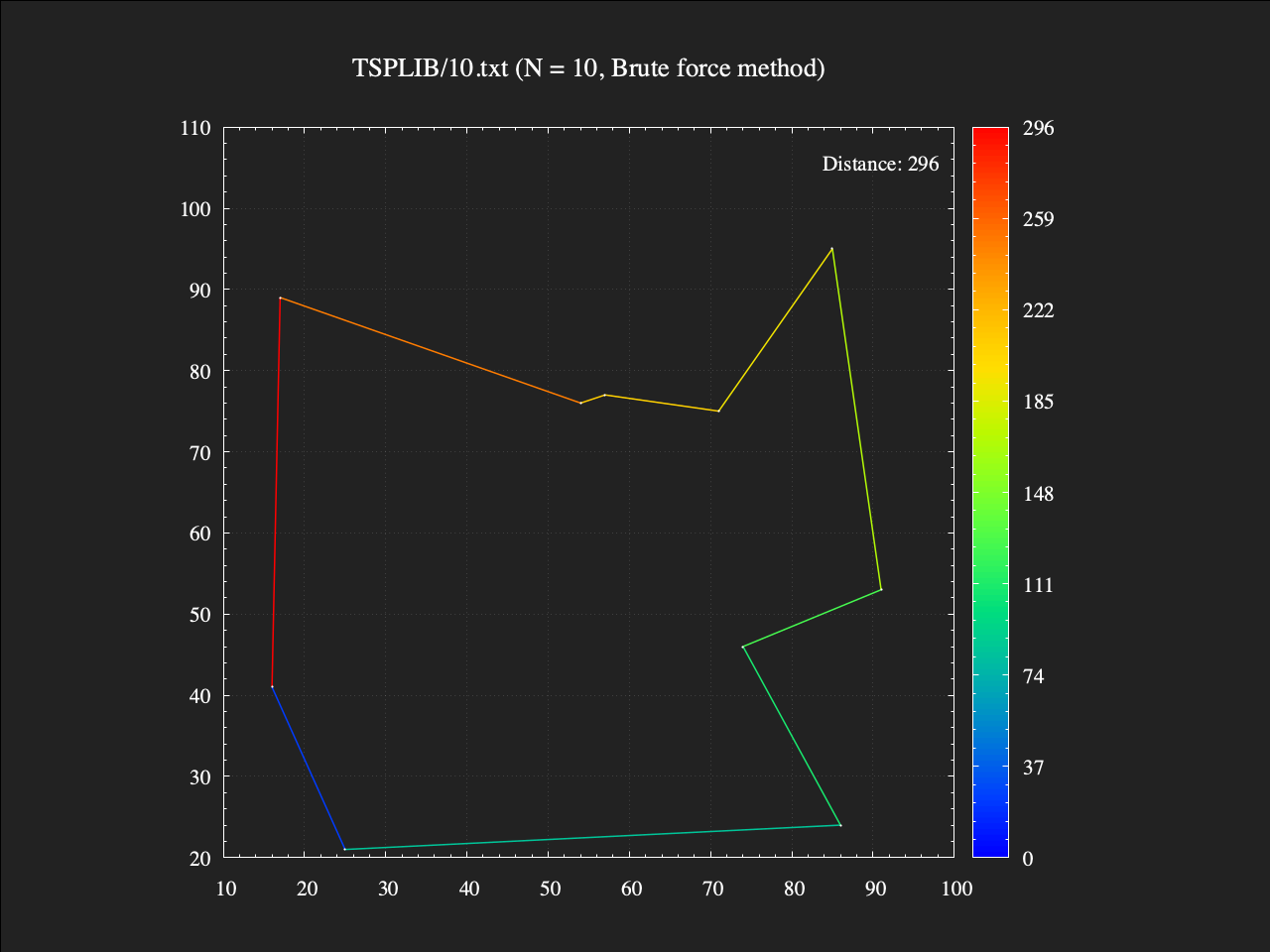
手元のMacBook（1.2 GHz Intel Core m3, 8 GB RAM）では約0.7秒で解けました。列挙した解の個数は$\frac{(10-1)!}{2}=181,440$個でした。

11都市TSP

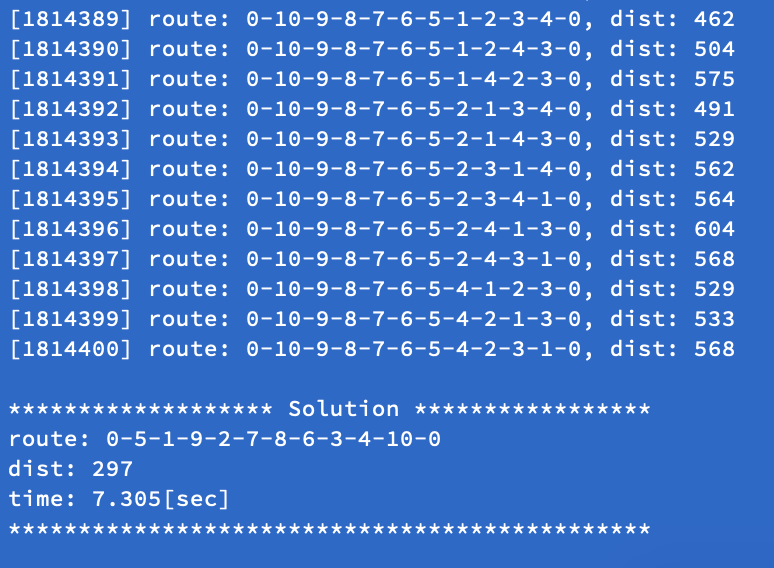
たった1点増やしただけですが、解の列挙数は$\frac{(11-1)!}{2}=1,814,400$個となり、計算時間も約7秒まで増えました。計算量として階乗オーダーで効いてくるので、10点->11点への変更で約10倍増えたのですね。

…

この調子で$n$を増やしていくと、例えば20点ですら既に現実的な計算時間で解を得るのが難しいのが分かると思います。更に30点になると解の候補の総数は$4.42×10^{30}$通りとなり、仮にスーパーコンピュータ「京」²を用いて解いたとしても、少なくとも1,000万年以上かかる見積もりになります。まさに天文学的数字になってしまい、現実的ではありません。何らかの計算上の工夫が必要なことが分かりますね！

組合せ最適化問題を解く上での計算の工夫として、大きく分けると厳密解法と近似解法の2つがあります。

厳密解法

改善解を逃さない範囲でなるべく探索を効率化しつつ大域最適解（TSPの場合、すべての巡回路の候補のうち最も距離が短いもの。以降は単に最適解と呼ぶことにします）を得る手法で、代表的なものとしては計算中に無駄な解の列挙を省く分枝限定法や、過去に得られた解の情報を表に書き込み、後々うまく利用しながら計算していく動的計画法がありますが、本記事では特段取り扱わないことにします。

近似解法

近似解法は、最適解は諦めつつも現実的な計算時間である程度良い解を得ようとする手法で、代表的なものとしてはグリーディ法（貪欲法）、少し発展的なものとしては局所探索法など、様々なものが提案されています。また、数学的な精度保証（最悪でも最適解と比べてこれ以上悪くなることはない、という保証）を与えることのできる場合があるのも特徴です。このうち、今回はグリーディ法について紹介していきます。

グリーディ法で解く

グリーディ法のアイデアはかなりシンプルで、基本的にはある時点における最適な操作を繰り返すだけです。以下、最近近傍法（nearest neighbor method）と呼ばれるTSPに対するグリーディ法の擬似コードを載せます。

nnm_pseudo_code.py

# 最近近傍法のpython擬似コード
def nnm():
    current = 出発する都市
    route = [ current ]

    while routeに含まれない都市が存在する:
        current = currentに一番近い未訪問の都市
        route.append( current )

    return route

現在の都市から最も近い未訪問の都市に移動することを繰り返し、すべての都市を訪問したら終了するという、簡単で直感的にも理解しやすいアルゴリズムであることがわかります。またすべての都市について、それらが未訪問かどうかを判定しつつ見ていくので、計算量は$O(n^2)$となります。

それでは最近近傍法を実際に試してみましょう。まずは総当たり法の際に7秒で解けた11都市の問題です。

11都市TSP

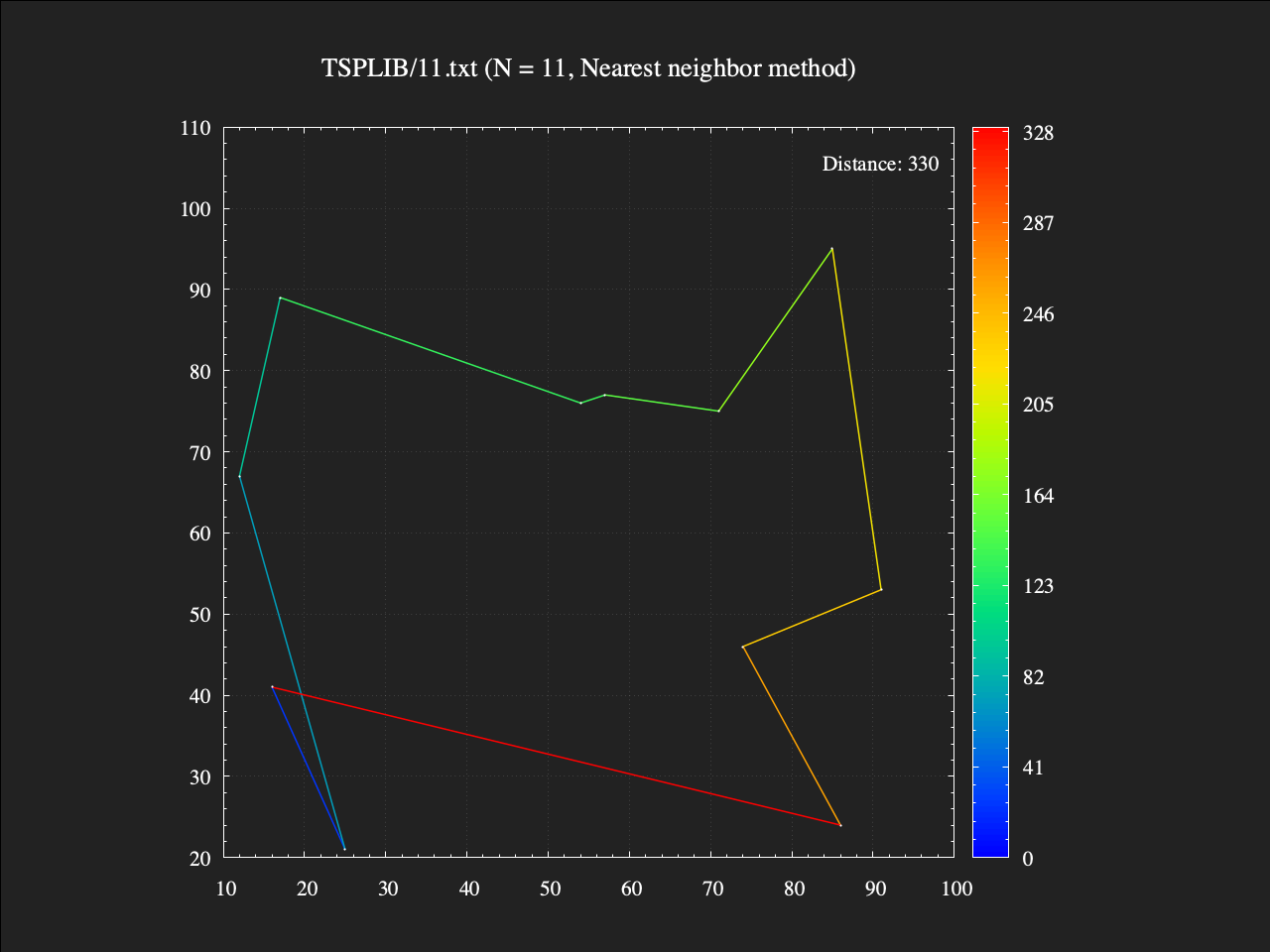
0.002秒で解けました。ですが解の総距離をよく見ると、総当たり法では297だったものが330となっており、またルートの見た目にも辺（2都市間を結ぶ線分）の交差があることから明らかに改善できる³部分があり、最適解ではないことがわかります。

ちなみに、図のルートの辺の色は出発からの累積距離を表しており、出発直後から 青 -> 緑 -> 黄 -> 橙 -> 赤 とグラデーションになるように設定しています。

48都市TSP

さらに、総当たり法では明らかに現実的な時間内で解けない規模の問題例も解いてみます。ちなみに実際のアメリカの都市の座標を用いた問題例となっており、TSPLIB⁴と呼ばれる有名なベンチマークにも含まれています。

0.005秒で解けたのは良いのですが、やっぱり辺が何箇所か交差してしまっており、解の改善の余地があることが分かります。

…

ここまで見てきたように、最近近傍法の欠点として、解の構築途中で現在地点の周囲に未訪問の都市が少なくなってくると遠い都市に移動せざるを得なくなり、結果として辺の交差が起きやすくなることが知られています。

このような欠点を補う手法として、解に含まれるいくつかの辺や点同士を交換することで解を改善していく手法（局所探索法）などがありますが、今回はここまでということで、次回以降書きたいと思います。

まとめ

• TSPの総当りは現実的な時間内には厳しい
• 近似解法だとそこそこ良い解を素早く出せる
• さらに局所探索法を適用することで解を改善できる（次回）

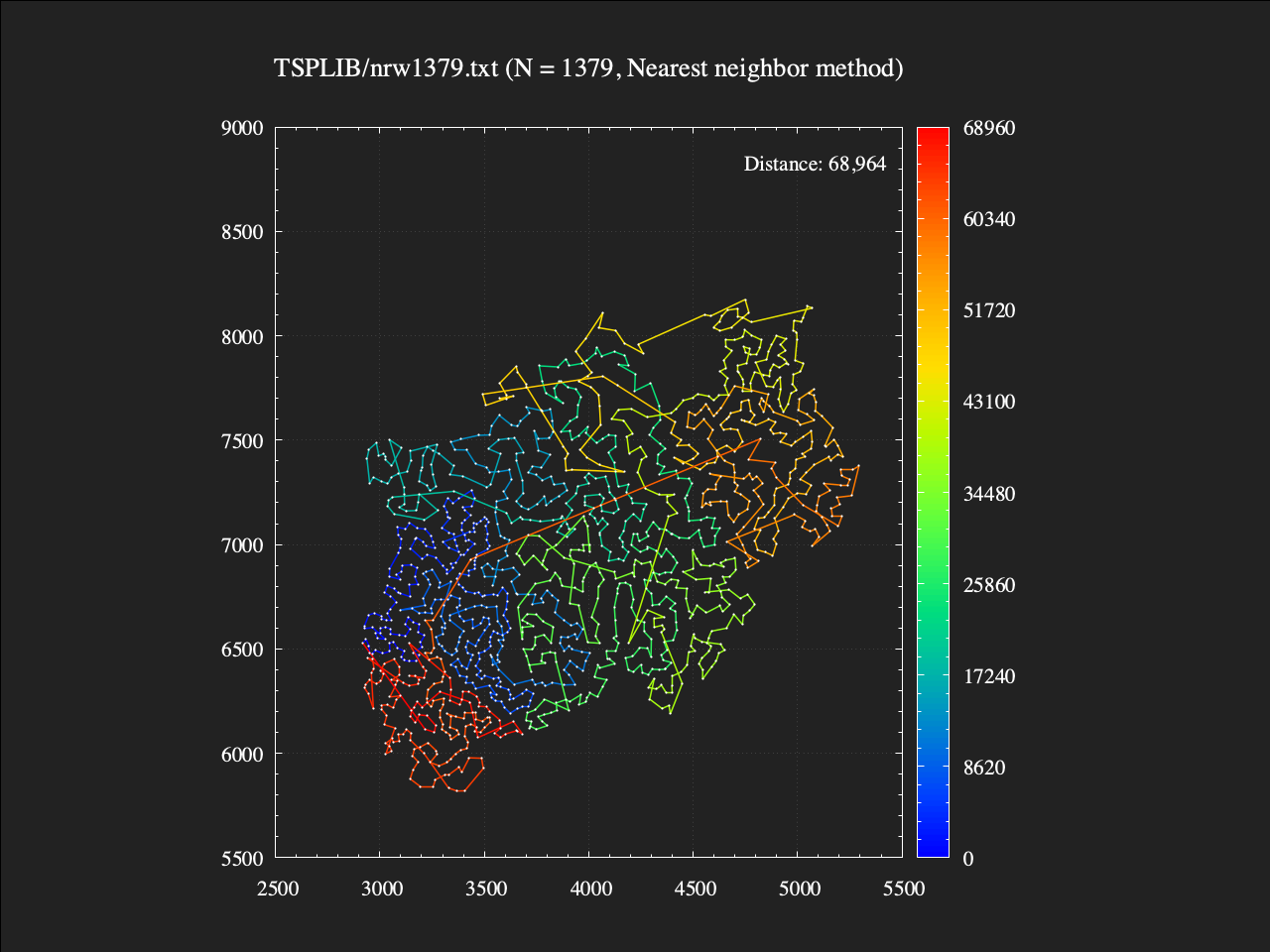
付録: 最近近傍法で1379都市TSP

計算時間は約1.3秒。解の構築途中、近くに未訪問点が無くなった場合にエリアを大きく横断するような辺が選ばれてしまっているのがよく分かる。

参考文献

柳浦睦憲 / 茨木俊秀 著、『組合せ最適化 -メタ戦略を中心として-』

1. 今回は対称TSP（都市A->都市Bの距離と都市B->都市Aの距離が同じとなるTSP。距離行列が対称行列となる）を仮定しているため。非対称TSPでは成り立たない。 ↩

2. スーパーコンピュータ「京」の計算能力は1京FLOPS（1秒間に$10^{16}$回の浮動小数点演算が可能）。 ↩

3. 各都市は2次元平面上にあり、かつ2都市間の距離はユークリッド距離を仮定しているため、三角不等式からほぼ自明。 ↩

4. TSPLIB: https://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/ ↩