はじめに
本記事は、巡回セールスマン問題をいろんな近似解法で解く（その1: 総当たり法とグリーディ法）の続きとなります。
前回の投稿から2年以上開いてしまいました…。
前回はTSPを総当たり法やグリーディ法で解き、それらの解がどうなるかを簡単に紹介しました。今回はグリーディ法で得た解に対して局所探索法という手法を用いることで、解をさらに改善できることを紹介していきたいと思います。
他の記事 （2022/05/30 追記）
他の記事へのリンクを以下に記載しましたので、ご興味ある方はぜひ読んでみてください。
局所探索法とは
ざっくりいうと、現在自分のいる場所から「周囲を見渡し」てみて、より良さそうな場所があればそこに移動する、ということを、これ以上改善できなくなるまで続けよう、というような考え方です。
上のアニメーションはある解$x_0$に対して局所探索法を適用した場合のイメージです。解$x_0$の周囲$N(x_0)$を見渡してみると、改善解$x_1$が見つかったので移動します。更に解$x_1$の周囲$N(x_1)$を見渡すとさらなる改善解$x_2$が見つかったため、また移動します。このような移動を改善解が見つけられなくなるまで繰り返します。この例では、解$x_k$に到達したところで改善解が見つからなくなったので、ここで終了です。
ここで、解$x$の「周囲を見渡す」ことで得られる解の集合$N(x)$を解$x$の近傍と呼びます。また、探索の入力として最初に与える解を初期解と呼び、アニメーションに出てきた$x_0$に対応します。さらに、局所探索の最後に到達した解はこれ以上改善できないため、局所最適解と呼び、アニメーション中の$x_k$に対応します。
局所探索法の擬似コードは以下のようになります。
# 局所探索法のpython擬似コード
def local_search(x_0 = 初期解):
x = x_0
N_x = x_0の近傍
while N_xに改善解が存在する:
x = xの近傍に含まれる改善解 # 改善解に移動
N_x = xの近傍 # 近傍を再評価
return x
ちなみに、近傍を評価する際に改善解が見つかれば即その解に移動することを即時移動戦略と呼び、近傍のすべての解を評価した上で最も改善幅の大きい改善解に移動することを最良移動戦略と呼んだりします。
近傍操作と2-opt近傍
さて、ここまでの説明では解の「周囲を見渡す」という曖昧な表現をしてきましたが、これは解を「少し変形」させるということに対応しており、近傍操作と呼んだりします。「少し変形」と言ってもまだ曖昧でよくわからないので、以下に例を示します。
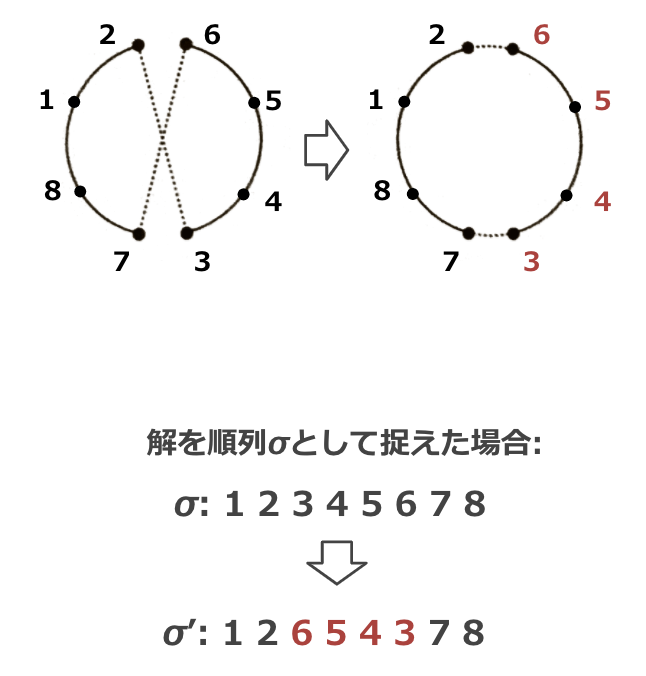
この例では、解に含まれる任意の2つの辺を付け替える操作である2-optという近傍操作を考えています。解を順列として捉えると、これは部分列の順序を反転させる操作に対応しています。図を見ると、確かに解が「少し変形」していることが分かります。ちなみに2-optはTSPに対する代表的な近傍操作のうちの1つであり、図で示したように辺の交差を解消するような働きをするため、解を改善する力が強いことがわかっています。
一般的に、都市数$n$のTSPの解$x$に対して2-optを適用することによって得られる解集合$N_\mathrm {2-opt}(x)$の要素数は、解に含まれる$n$個の辺から2つ選んで付け替えるという操作の総数となるため、$O(n^2)$となります（実際は逆順にすると等価な解などが含まれるため、厳密な$n^2$よりは少なくなります）。また、$N_\mathrm {2-opt}(x)$は2-optによって得られる解集合であるため、特に2-opt近傍と呼ぶこともあります。さきほどの局所探索法の説明に出てきた近傍$N(x)$の一例というわけですね。
...
それでは、前回の記事に出てきた48都市TSPに対するグリーディ法の解に対して、2-optを用いた局所探索法を適用してみましょう。比較のため、適用前の解も載せています。使用した計算機はMacBook Pro（1.4 GHz クアッドコア Intel Core i5, 16 GB RAM）です。
48都市TSP
この問題例は最適値（すべての解の中で最も小さい総距離）が求められており、その総距離は10628です1。
適用前
総移動距離は12861であり、最適値に対しておよそ+21.0%という結果。計算時間は0.003秒であった。構築が進むにつれて遠い点への移動が避けられなくなるという最近近傍法の特徴が見えている。また、数カ所で辺の交差が起きているため、これらを取り除くことができれば総距離をもっと小さくできそう。
適用後
総移動距離は11010であり、最適値に対しておよそ+3.6%の結果。計算時間は0.004秒であり、これには最近近傍法による初期解構築の時間も含めている。たった0.001秒の増加にも関わらず、最適値からの差を+21.0%から+3.6%へ大幅に改善出来ていることが分かる。また、適用前に生じていた辺の交差もすべて取り除くことができた。
...
さらに、前回の記事の最後に紹介した1379都市TSPに対するグリーディ法の解に対しても2-optによる局所探索法を適用してみます。
1379都市TSP
この問題例も最適値が求められており、その総距離は56638です1。
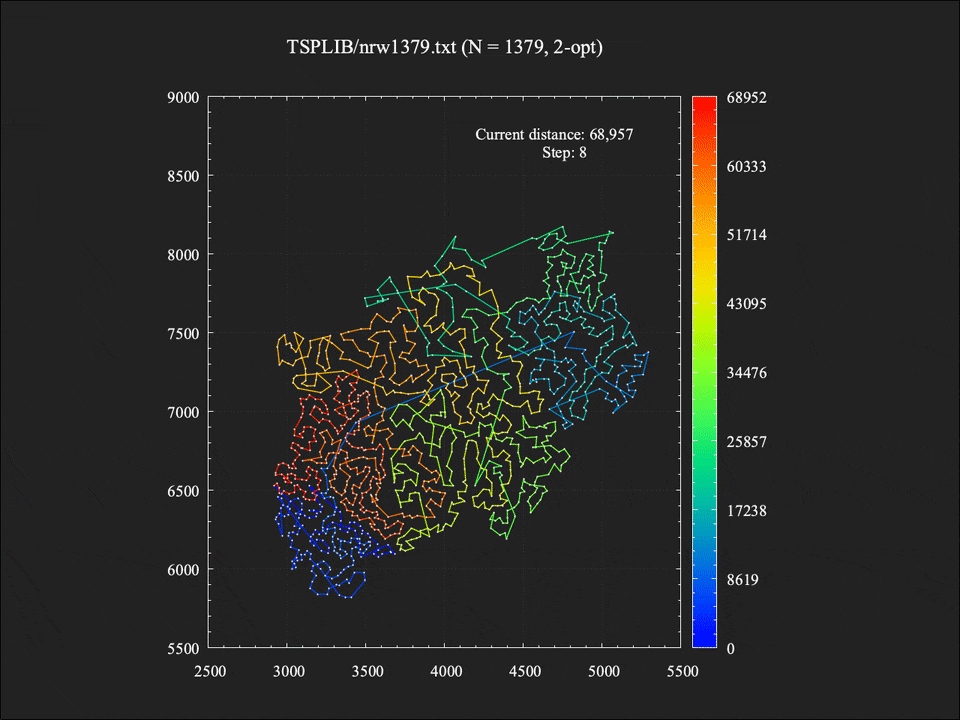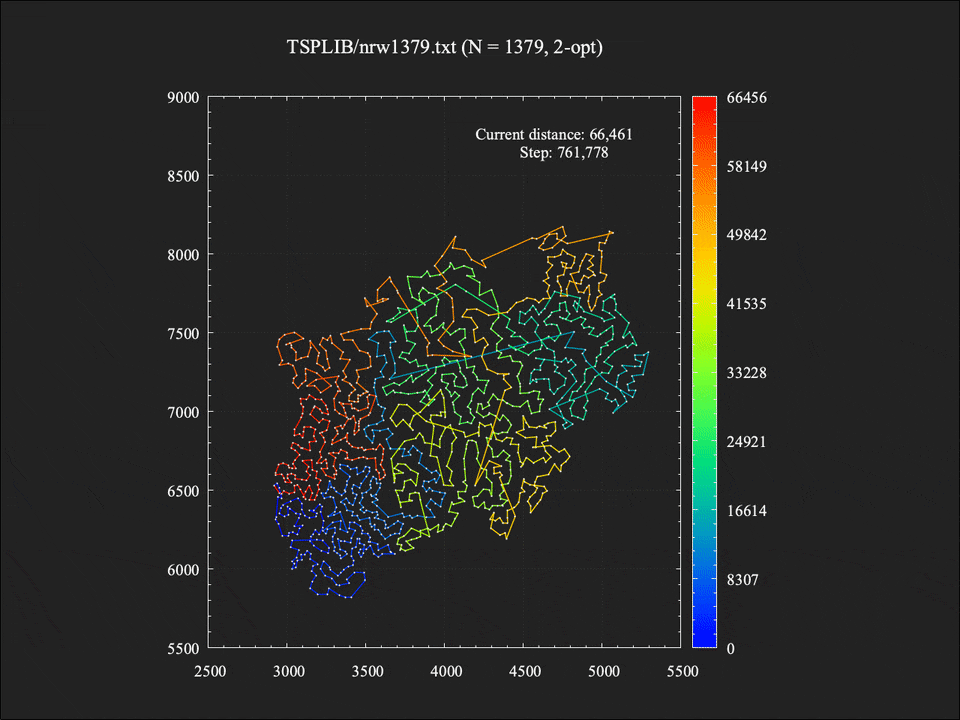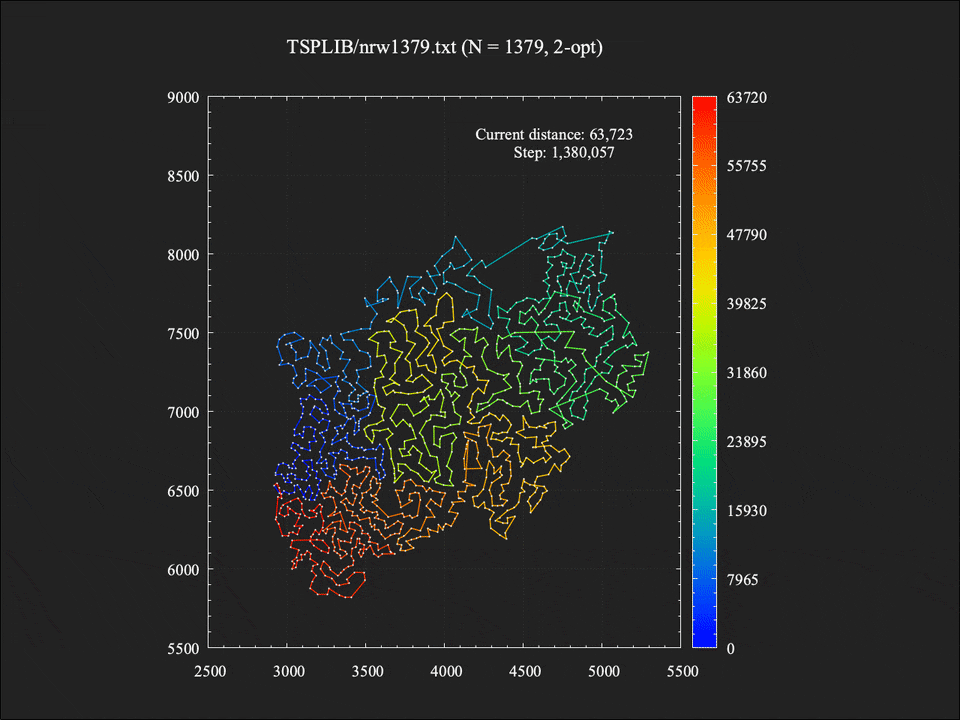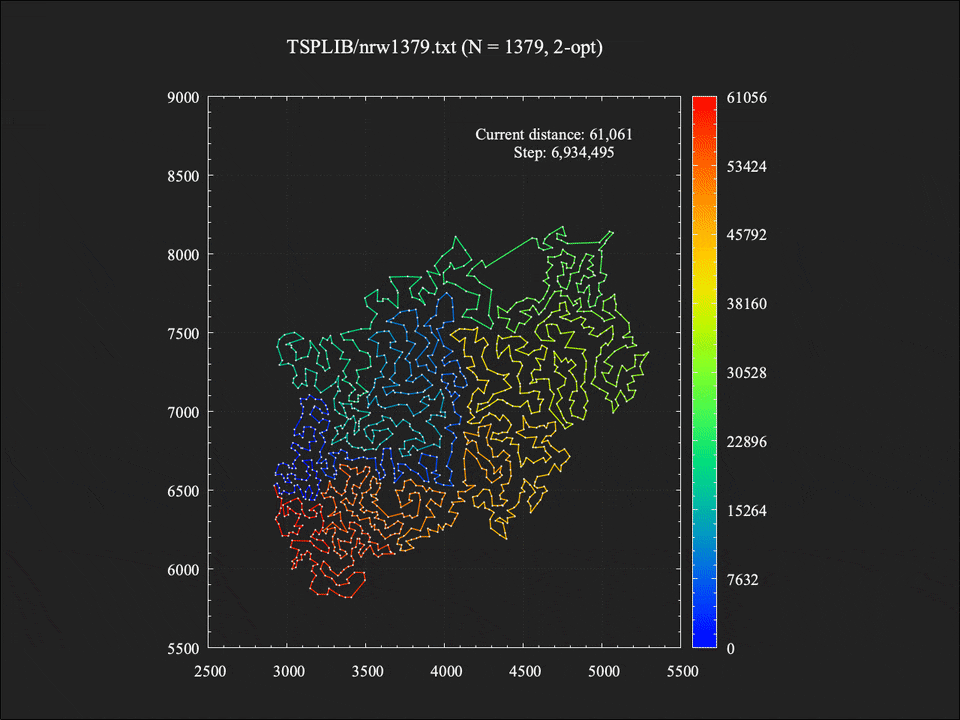
適用前
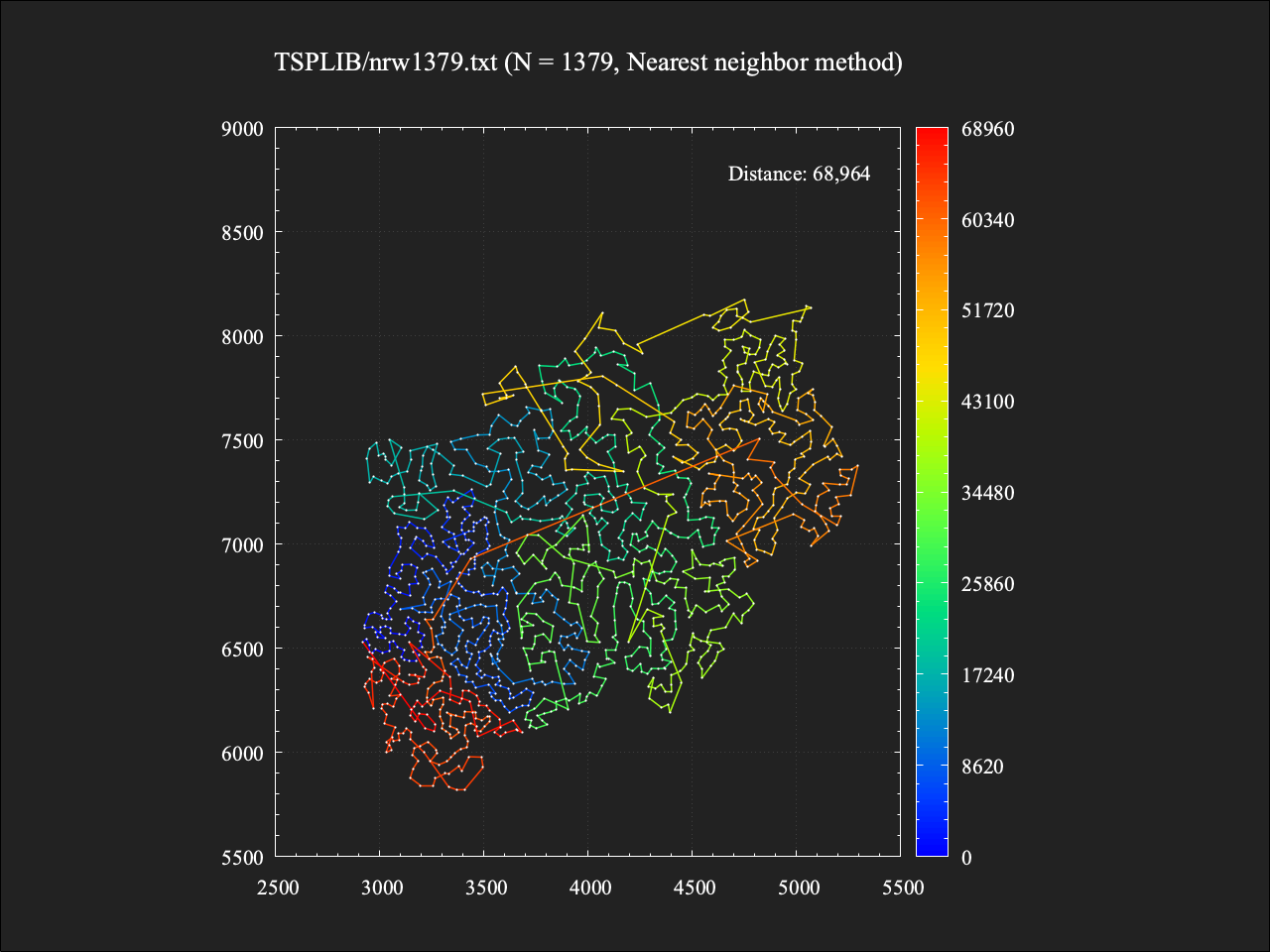
総移動距離は68964であり、最適値に対しておよそ+21.8%という結果。計算時間は約1秒であった。かなりの箇所で辺が交差しており、まだまだ改善の余地がありそう。
適用後
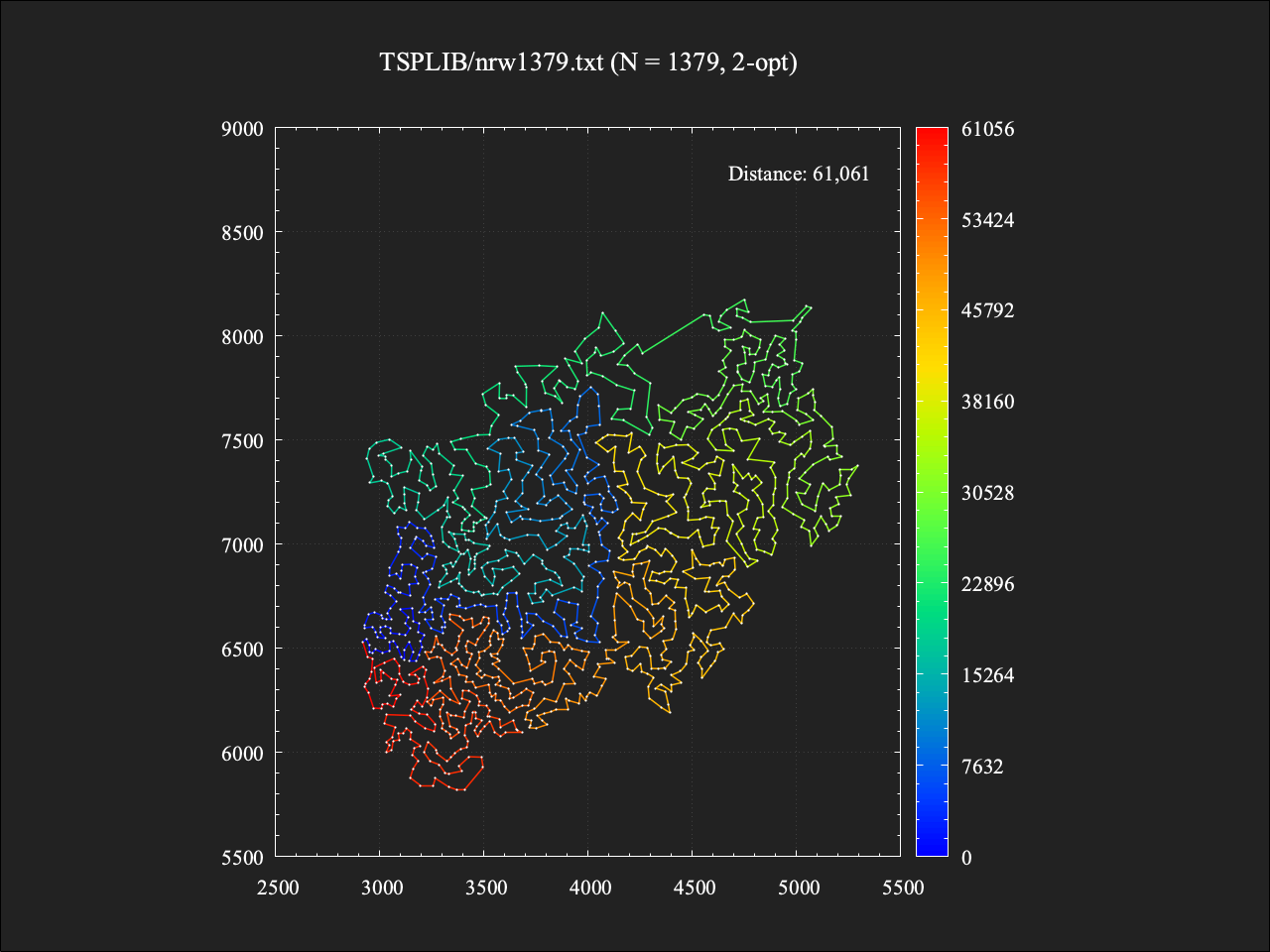
総移動距離は61061であり、最適値に対しておよそ+7.8%という結果。計算時間は約1.4秒であった。48点の問題例ほどの改善は見られなかったものの、辺の交差もすべて取り切っており、ぱっと見でも悪くないな、と感じられるような解が得られている（感じ方は人それぞれなので個人差があるかもしれません…）。
...
局所探索法を適用することで、現実的な時間で解を大きく改善できることがわかりました。
今回紹介した2-optを繰り返し適用するだけでも、人間の目で見てそれほど違和感のない解が得られるのですが、例えば3つの辺の付け替えによって得られる3-opt近傍や、解に含まれる都市を1つ選んで他の位置に挿入する挿入近傍、都市を2つ選んで互いの位置を交換する交換近傍など、他の近傍も組み合わせて探索することで、2-optのみでは到達できない解空間の探索が可能となるため、更なる解の改善が見込めます。
また、今回は初期解として最近近傍法で生成したものを使用していましたが、そこにランダム要素を加えて複数の初期解から局所探索を始めることで探索の多様性を広げる多スタート局所探索法などもあり、次回はそのあたりを解説していければ、と思います。
まとめ
- 局所探索法を用いることで、解を現実的な時間で大きく改善できる
- 複数の初期解を利用することで更に改善できる（次回）
付録: 局所探索法（2-opt）のアニメーション
局所探索中に改善解への移動が395回起きていたため、それらのスナップショットをすべてつなぎ合わせてアニメーションにしてみました。Stepは2-opt近傍操作を評価した回数の累計です。探索が進むにつれて辺の交差が徐々に少なくなり、それにしたがって総距離も減少していく様子が分かります。ちなみに実際の計算時間は約1.4秒でしたが、アニメーションの分かりやすさのため10倍ほどスローに再生しています。
参考文献
柳浦睦憲 / 茨木俊秀 著、『組合せ最適化 -メタ戦略を中心として-』
おわりに
ここまで読んでいただきありがとうございました。
株式会社オプティマインドでは、一緒に働く仲間を大募集中です。
カジュアル面談も大歓迎ですので、気軽にお声がけください。
【エンジニア領域の募集職種】
●ソフトウェアエンジニア
●QAエンジニア
●Androidアプリエンジニア
●組合せ最適化アルゴリズムエンジニア
●経路探索アルゴリズムエンジニア
●バックエンドエンジニア
●インフラエンジニア
●UXUIデザイナー
【ビジネス領域の募集職種】
●セールスコンサルタント
●上場準備担当
『Loogiaってどんなサービス？』については、こちら
Wantedlyでもこちらで募集中