はじめに
本記事は、巡回セールスマン問題をいろんな近似解法で解く(その5: 焼きなまし法)の続きとなります。他の記事へのリンクを以下に記載しましたので、ご興味ある方はぜひ読んでみてください。
他の記事
さまざまな近傍
ここまでの連載ではTSPに対する局所探索法や焼きなまし法など様々な手法を紹介してきましたが、それらの内部に組み込まれた近傍操作は2-opt近傍のみでした。今回はまずはじめに2-opt以外の代表的な近傍についてご紹介し、複数の近傍を用いることの利点をざっくり説明したあと、前回紹介した焼きなまし法に対していくつかの近傍操作を追加で組み込むことで探索の多様性が向上し、より良い解が得られることを見ていきたいと思います。
挿入近傍
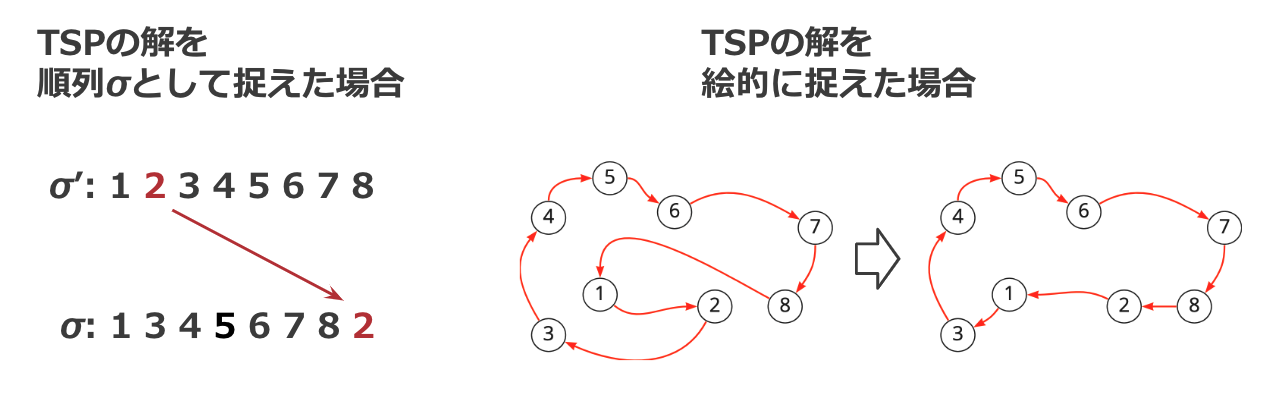
TSP以外の最適化問題でもよく利用される近傍の一つで、解に含まれる1つの要素を他の位置に挿入することで得られる近傍となります。TSPの場合、解を順列として捉えたときにある1つの数字を他の位置に移動させるイメージです。
交換近傍
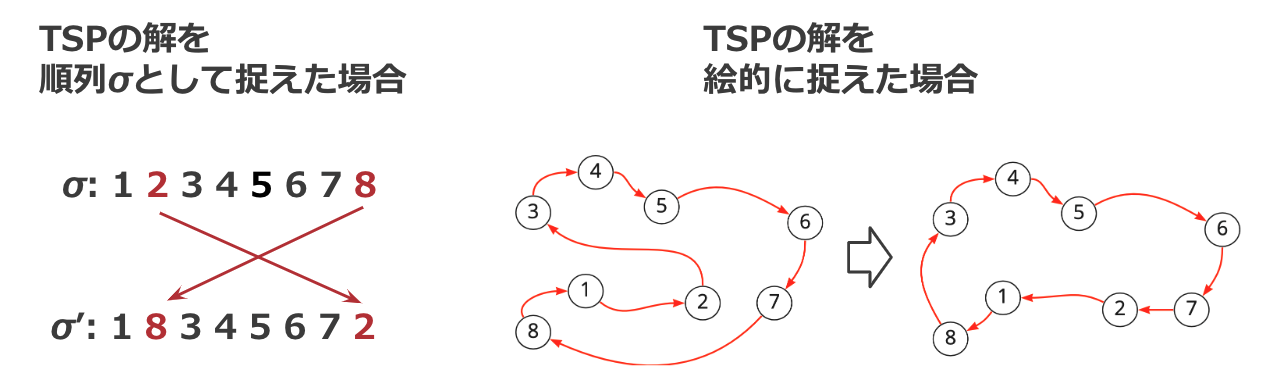
こちらもTSP以外の最適化問題でもよく利用される近傍の一つで、解に含まれる2つの要素の位置を交換することで得られる近傍です。TSPの場合、解を順列として捉えたときに2つの数字の位置を交換するイメージとなります。
Or-opt近傍
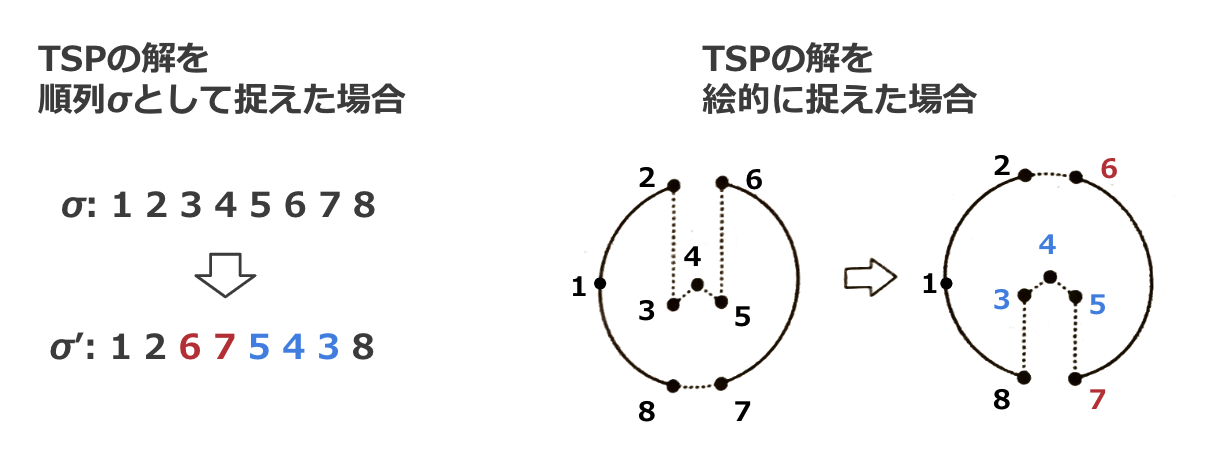
こちらは解において連続する3本以下の枝を他の位置に挿入することで得られる近傍となります。
λ-opt近傍
2-opt近傍を一般化した近傍であり、たかだかλ本の枝を付け替えることにより得られる解の集合となります。3-opt近傍がOr-opt近傍を部分集合として含んでいることや、4-opt近傍が反復局所探索法(2-opt)のkickとして効果的であることなど興味深い内容が多く含まれますが、今回の記事では省略します。
複数の近傍を使うと何が嬉しい?
ここまで新しい近傍をいくつかご紹介しましたが、単一の近傍を使う場合に比べて複数の近傍を使うと何が嬉しいのでしょうか?複数の近傍を使うほうが良い探索ができそうだというのは何となく直感的に分かると思うのですが、ポイントはある近傍の局所最適解は他の近傍の局所最適解とは限らない、ということです。
例えばある8都市の問題例に対する最適解が1-2-3-4-5-6-7-8であるとし、現在の解が1-2-6-5-4-3-7-8であるとしましょう。現在の解をよく見ると、部分列6-5-4-3を反転させれば最適解となることがわかります。ここで、現在の解から最適解に移動するのに挿入近傍だけしか使えないとすると、1回の操作でこの部分列を反転させることは不可能であり、少なくとも操作を3回繰り返す必要があることがわかると思います。しかし第2回の記事でご紹介したとおり、部分列の反転は2-opt近傍操作と等価であるため、2-opt近傍を用いる場合は操作を1回行うだけで最適解にたどり着けることがわかります。
以上のことからも分かる通り、ある近傍に関する1回の操作でたどり着くことのできる解は他の近傍に関する1回の操作でたどり着ける解とは基本的に異なるため、複数の近傍を使うことで探索の多様性が高まり、より良い解を見つけやすくなります。ただし、実際は近傍操作の種類ごとに計算量が異なる場合もあるため、闇雲に近傍をたくさん使えば良いというわけでもなく、問題の構造や近傍の性質を注意深く観察した上で適切なものを選ぶことが重要だと思います。
焼きなまし法に近傍操作を追加してみる
前回紹介した焼きなまし法では近傍として2-opt近傍のみを考えていましたが、そのアルゴリズムに対して今回はOr-opt近傍と3-opt近傍を追加で組み込んでみたいと思います。組み込み方は至ってシンプルで、whileループの最初で近傍解を選ぶ際、2-opt近傍、Or-opt近傍および3-opt近傍の解の中からパラメータで指定した確率に応じて選ぶようにしました。以下に疑似コードを示します。
疑似コード
# 焼きなまし法(2-opt, 3-opt, Or-opt)のpython擬似コード
def simulated_annealing_multiple_neighbors(x_0 = 初期解, t_0 = 初期温度, c = 冷却率):
x_current = x_best = x_0 # x_current, x_bestを初期解で初期化
t = t_0 # 温度を初期化
while 終了条件を満たさない:
N = N_2opt, N_3opt, N_oroptの中から指定確率で選んだ近傍
x = 近傍Nに関するx_currentの近傍解からランダムに選んだ解
d = f(x) - f(x_current) # f: 評価関数
if d <= 0:
x_current = x # 改善解ならば常に移動する
if f(x) < f(x_best):
x_best = x
elif rand() <= e ** (-d / t): # e: ネイピア数, rand: 0以上1以下のランダムな実数を返す関数
x_current = x # 改悪解であっても、温度と改悪幅に応じた確率で移動する
t = c * t # 冷却する
return x_best
実験
それでは今回の手法をいくつかの問題例に適用してみます。使用した計算機はMacBook Pro(1.4 GHz クアッドコア Intel Core i5, 16 GB RAM)です。
...
48都市TSP
この問題例は最適値(すべての解の中で最も小さい総距離)が求められており、その総距離は10628です1。
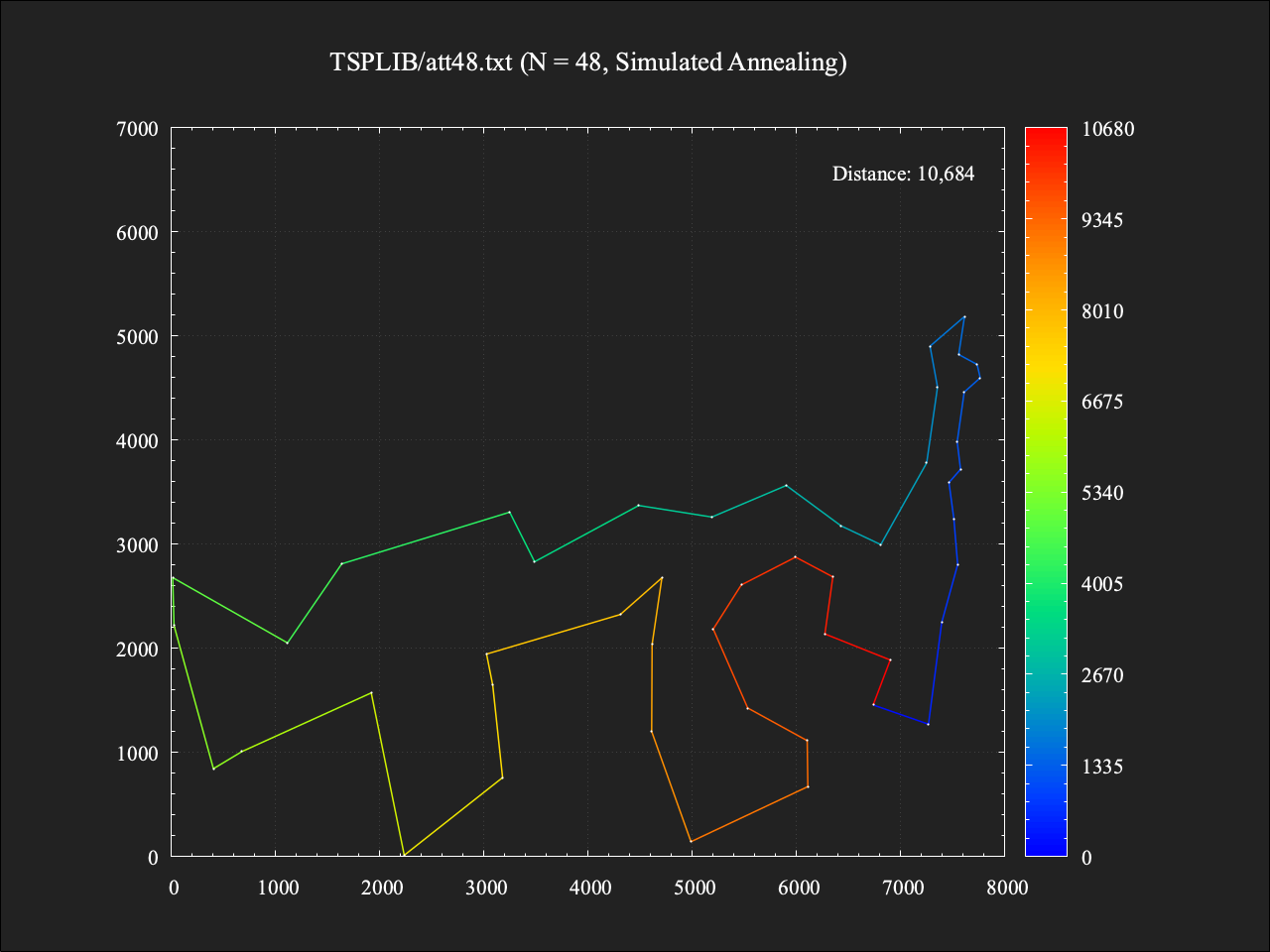
総移動距離は10684であり、最適値に対しておよそ+0.53%の結果。計算時間は0.011秒であった。
...
1379都市TSP
この問題例も最適値が求められており、その総距離は56638です1。
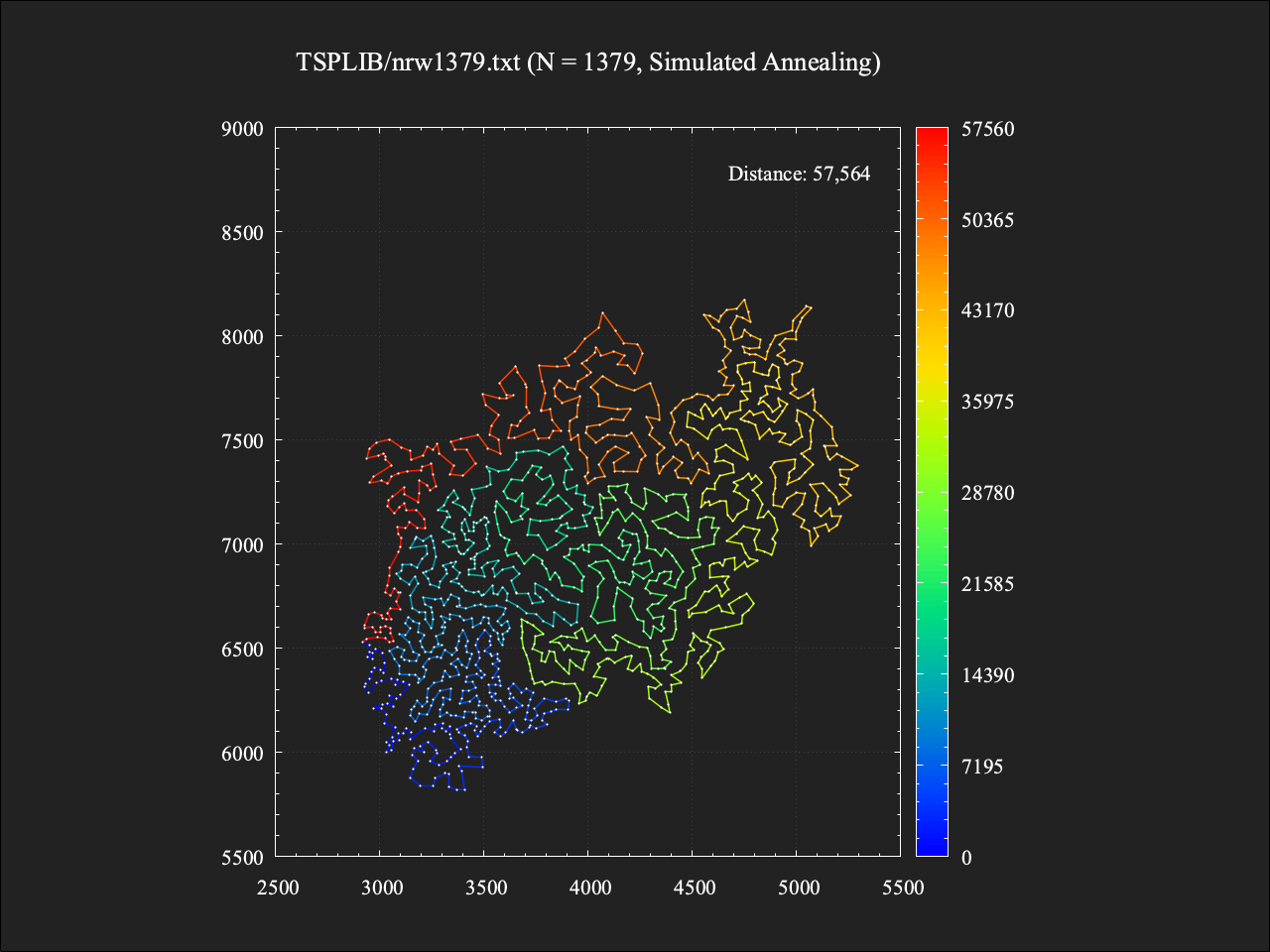
総移動距離は57564であり、最適値に対しておよそ+1.6%という結果。計算時間は約3.9秒であった。前回の焼きなまし法の結果を更に更新できた。
これまでの手法の結果と比較
表
| att48(10628) | kroA100 (21282) |
tsp225 (3916) |
att532 (27686) |
nrw1379 (56638) |
|
|---|---|---|---|---|---|
| その1: 最近近傍法 | 12861 0.000秒 |
27807 0.000秒 |
5030 0.000秒 |
35516 0.000秒 |
68964 0.000秒 |
| その2: 局所探索法 (最近近傍法+2-opt) |
11010 0.002秒 |
22399 0.002秒 |
4304 0.013秒 |
29739 0.192秒 |
61061 0.435秒 |
| その3: GRASP法 (ランダム化最近近傍法+2-opt) |
10895 0.013秒 |
21843 0.014秒 |
4158 0.103秒 |
29320 1.142秒 |
60512 5.009秒 |
| その4: 反復局所探索法 (2-opt+double bridge) |
10739 0.013秒 |
22177 0.022秒 |
4208 0.099秒 |
29718 1.036秒 |
61061 4.317秒 |
| その5: 焼きなまし法 (2-opt) |
10711 0.012秒 |
22190 0.016秒 |
3988 0.060秒 |
28591 0.834秒 |
58572 3.966秒 |
| 今回: 焼きなまし法 (2-opt, 3-opt, Or-opt) |
10684 0.011秒 |
21381 0.020秒 |
3965 0.056秒 |
28141 0.991秒 |
57564 3.853秒 |
これまでの連載で紹介してきた手法の結果をまとめた表です。問題例名の下の丸括弧は最適値を表しています。また、各問題例においてこれまで紹介した手法の中でベストな総距離の値を太字で示しています。さらに、今回から総距離の下に計算時間も記載しました。
結果と考察
過去記事の焼きなまし法やGRASP法、反復局所探索法の結果との比較を行いたかったため、それらのアルゴリズムにかかった秒数と同程度となるようにそれぞれの問題例で終了条件と冷却率を調整した上で実験しました。前回も注意書きした通り、今回もラフな比較実験のため参考程度の結果ではありますが、すべての問題例で同程度の時間でもより良い解が得られていることがわかります。
ある近傍に対する局所最適解は他の近傍における局所最適解とは限らないということもあり、2-opt近傍のみを使うよりも複数の近傍を使ったほうがより良い解が得られているのは自然な結果かと思います。またコストの更新幅も大きいことから、組合せ最適化に対するアルゴリズムの設計において近傍を適切に選ぶことはフレームワーク(焼きなまし法や反復局所探索法などのメタヒューリスティック)を工夫するのに劣らないくらい重要な要素であることがわかります。
まとめ
複数の近傍を用いることで単一の近傍を用いる場合よりも多様な探索を行うことができ、その結果より良い解が得られることがわかりました。
この連載は今回で最終回となります。ここまで読んでいただきありがとうございました!
参考文献
柳浦睦憲 / 茨木俊秀 著、『組合せ最適化 -メタ戦略を中心として-』
おわりに
株式会社オプティマインドでは、一緒に働く仲間を大募集中です。
カジュアル面談も大歓迎ですので、気軽にお声がけください。
【エンジニア領域の募集職種】
●ソフトウェアエンジニア
●QAエンジニア
●Androidアプリエンジニア
●組合せ最適化アルゴリズムエンジニア
●経路探索アルゴリズムエンジニア
●バックエンドエンジニア
●インフラエンジニア
●UXUIデザイナー
【ビジネス領域の募集職種】
●セールスコンサルタント
●オペレーションコンサルタント
『オプティマインドってどんな会社?』については、こちらから
Wantedlyでもこちらで募集中