はじめに
本記事は、巡回セールスマン問題をいろんな近似解法で解く(その3: ランダム化最近近傍法とGRASP法)の続きとなります。
前回はランダム化最近近傍法を用いたGRASP法をご紹介しました。GRASP法では複数の初期解から局所探索を始めることで解の探索の多様性が増すことを見ましたが、今回はGRASP法とはまた違った方向性で探索の多様性を広げた手法である反復局所探索法をご紹介します。
他の記事 (2022/05/30 追記)
他の記事へのリンクを以下に記載しましたので、ご興味ある方はぜひ読んでみてください。
反復局所探索法
以前にこちらの記事で扱いましたが、局所探索法は解に対してそれ以上改善ができなくなるまで近傍操作を加え続けることで局所最適解を見つける手法であり、一度局所最適解を見つけてしまえばそれで終了となるため、解の探索の多様性という観点では課題がありました。反復局所探索法は局所最適解に対してkickと呼ばれる少しの変形を加えた解を新たな初期解として局所探索法を行う、ということを反復する手法であり、アルゴリズムの中で複数の局所最適解を評価することが可能であるため、通常の局所探索法に比べて探索の多様性が高くなります。疑似コードを以下に載せます。
# 反復局所探索法のpython擬似コード
def iterated_local_search(x_0 = 初期解):
x_best = local_search(x_0)
while 終了条件を満たさない:
x_seed = x_best # 各反復において暫定解x_bestから探索を始める
x_kicked = kick(x_seed) # x_seedにkickを加える
x = local_search(x_kicked)
if xがx_bestよりも良い解である:
x_best = x
return x_best
local_search関数としては、例えばこれまでの連載でもおなじみの2-opt近傍による局所探索を用いることが出来るでしょう。またkick関数は局所最適解の周辺の解領域から大きく移動できるような操作であることが望ましいです。局所探索に用いる近傍と同じものを用いても良いのですが、kick後の解が局所探索に用いている近傍内に含まれる場合が多いと考えられるため、局所探索中にkick前の解に戻ってしまう可能性があります。これを防ぐため、kickには局所探索に用いる近傍とは別のものを用意する場合が多く、例えば局所探索に2-opt近傍を用いる場合はkickとしてdouble bridge近傍を利用するのが効果的であると言われています。double bridge近傍操作では、以下の図の点線で示した辺の付け替えが行われます。

この近傍では4つの辺の付け替え操作が行われるため、4-opt近傍の特別な場合とみなすことができます。この近傍は2-opt近傍操作を2回繰り返しても到達できないような解の集合となっているため、局所探索として2-opt近傍を採用した場合にkick前の解にすぐに戻ってしまうことを防ぐ効果が高いと考えられます。
...
それでは2-opt近傍による局所探索法とdouble bridge近傍によるkickを用いた反復局所探索法をいくつかの問題例に適用してみます。iterated_local_search関数に与える初期解としてはこれまでも扱ってきた最近近傍法による解を利用しました。また、反復局所探索法の終了条件はイテレーション10回としました。使用した計算機はMacBook Pro(1.4 GHz クアッドコア Intel Core i5, 16 GB RAM)です。
48都市TSP
この問題例は最適値(すべての解の中で最も小さい総距離)が求められており、その総距離は10628です1。
結果

総移動距離は10739であり、最適値に対しておよそ+1.0%の結果。計算時間は0.010秒であった。
1379都市TSP
この問題例も最適値が求められており、その総距離は56638です1。
結果
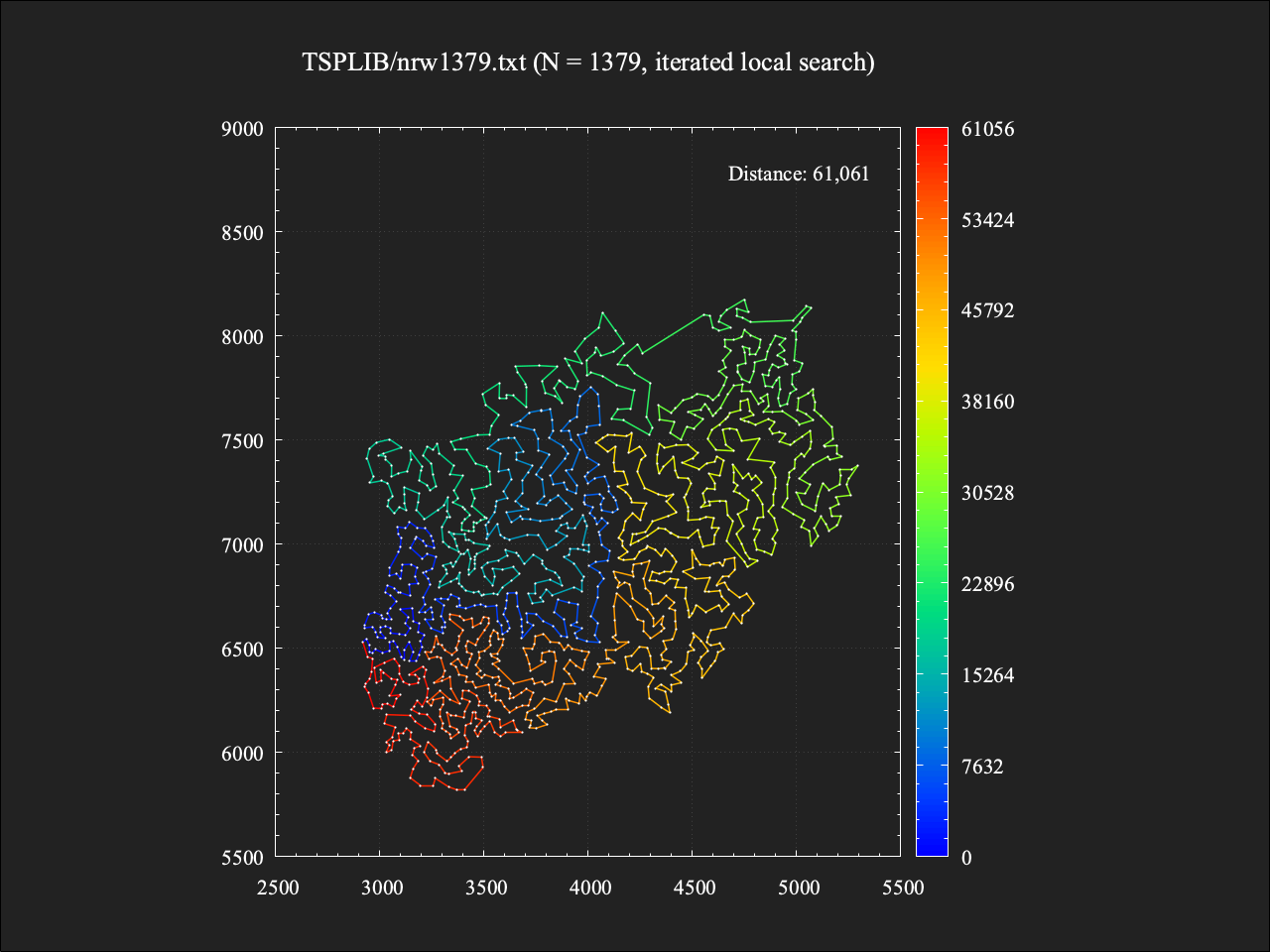
総移動距離は61061であり、最適値に対しておよそ+7.8%という結果。計算時間は約4.5秒であった。この解は第二回の記事で紹介した手法による結果(最近近傍法で得た初期解に対して2-opt近傍による局所探索法を適用したもの)と同じものであり、局所探索(+kick)を反復しても初期解よりも良い解を得ることができなかったものと思われる。
これまでの手法の結果を比較
| att48(10628) | kroA100 (21282) |
tsp225 (3916) |
att532 (27686) |
nrw1379 (56638) |
|
|---|---|---|---|---|---|
| その1: 最近近傍法 | 12861 | 27807 | 5030 | 35516 | 68964 |
| その2: 局所探索法 (最近近傍法+2-opt) |
11010 | 22399 | 4304 | 29739 | 61061 |
| その3: GRASP法 (ランダム化最近近傍法+2-opt) |
10895 | 21843 | 4158 | 29320 | 60512 |
| 今回: 反復局所探索法 (2-opt+double bridge) |
10739 | 22177 | 4208 | 29718 | 61061 |
これまでの連載で紹介してきた手法の結果をまとめた表です。att48とnrw1379はこれまで48都市TSP、1379都市TSPとして扱ってきた問題例です。問題例名の下の丸括弧は最適値を表しています。また、各問題例においてこれまで紹介した手法の中でベストな総距離の値を太字で示しています。
アルゴリズムの性質上、反復局所探索法は局所探索法と同等かそれ以上の結果が得られるはずであり、たしかにそのような結果が得られているものの、前回紹介したGRASP法と比べた場合は必ずしもどちらが高性能であるとは言えなさそうです。ただし今回ご紹介した反復局所探索法は最もシンプルな形式のものであり、例えばkickに採用する近傍を1種類ではなく複数種類用意することで探索の多様性を更に増やすことができます(今回は割愛)。
...
まとめ
局所探索法による局所最適解の探索とkickによる局所最適解からの脱出を反復することによって、単純な局所探索法よりも多様な解の探索を行うことが可能となり、より良い解を得られることがわかりました。
次回は解遷移時の評価値の改悪幅および「温度」と呼ばれるパラメータに依存するような確率で改悪解への移動も許容することで、探索の序盤では多様な探索を、終盤では集中的な探索を行うことの出来る焼きなまし法についてご紹介したいと思います。
参考文献
柳浦睦憲 / 茨木俊秀 著、『組合せ最適化 -メタ戦略を中心として-』
おわりに
ここまで読んでいただきありがとうございました。
株式会社オプティマインドでは、一緒に働く仲間を大募集中です。
カジュアル面談も大歓迎ですので、気軽にお声がけください。
【エンジニア領域の募集職種】
●ソフトウェアエンジニア
●QAエンジニア
●Androidアプリエンジニア
●組合せ最適化アルゴリズムエンジニア
●経路探索アルゴリズムエンジニア
●バックエンドエンジニア
●インフラエンジニア
●UXUIデザイナー
【ビジネス領域の募集職種】
●セールスコンサルタント
●オペレーションコンサルタント
『オプティマインドってどんな会社?』については、こちらから
Wantedlyでもこちらで募集中