はじめに
本記事は、巡回セールスマン問題をいろんな近似解法で解く(その2: 局所探索法と2-opt近傍)の続きとなります。
前回は最近近傍法で得られた初期解に対して2-optを用いた局所探索法を適用することで解を大きく改善できることを紹介しました。今回は最近近傍法にランダム性を加えたランダム化最近近傍法と、その解に対して局所探索法を適用することを繰り返すGRASP法と呼ばれる手法を用いることで探索の多様性が広がり、更に解を改善できることを見ていきたいと思います。
他の記事 (2022/05/30 追記)
他の記事へのリンクを以下に記載しましたので、ご興味ある方はぜひ読んでみてください。
ランダム化最近近傍法
最近近傍法は過去にこちらの記事で扱いましたが、簡単に言うと「現在の都市から最も近い未訪問の都市に移動することを繰り返し、すべての都市を訪問したら終了する」というグリーディ法に基づいたアルゴリズムでした。一方、ランダム化最近近傍法においては現在の都市から最も近い都市に移動するとは限らず、現在の都市に近い上位$k$都市の集合の中からランダムに1都市を選び、移動します。以下に擬似コードを示します。
# ランダム化最近近傍法のpython擬似コード
def randomized_nnm():
current = 出発する都市
route = [ current ]
while routeに含まれない都市が存在する:
nearest_set = routeに含まれない都市のうちcurrentに近い上位k都市の集合
current = nearest_setからランダムに選んだ都市
route.append( current )
return route
なお、$k=1$とした場合はもとの最近近傍法と同じものになります。
また、nearest_setの決め方として、currentから最も近い未訪問の都市までの距離を$d_{min}$とし、$α$を1以上の定数として、currentから$α \cdot d_{min}$以内の距離にある未訪問の都市の集合で与える手法もありますが、今回は割愛します。こちらの手法も$α=1$とした場合はもとの最近近傍法と同様の動作となります。
...
グリーディ法はそのアルゴリズムの性質上、複数の多様な解を生成するのには向いていませんが、そこにランダム性を加えたランダム化グリーディ法では、解に多様性を持たせることができます。この性質を局所探索法に応用した手法が以下にご紹介するGRASP法になります。
GRASP法
簡単に述べると、ランダム化グリーディ法によって得られた初期解に対して局所探索法を適用する、ということを反復し、その中で得られた実行可能な最良解を出力する手法となります。1989年にFeoとResendeらによって提案されました。ちなみにGRASPとは"greedy randomized adaptive search procedure"の略のようです。以下に擬似コードを示します。
# GRASP法のpython擬似コード
def grasp():
best = 空の解
while 終了条件を満たさない:
init = randomized_greedy()
current = local_search(init)
if bestが空の解である or currentがbestよりも良い解である:
best = current
return best
TSPに対してGRASP法を適用することを考えると、whileループの終了条件としては、シンプルにイテレーション数の制限や計算開始からの経過時間の制限が与えられる場合が多いと思います。randomized_greedy関数にはまさに今回説明したランダム化最近近傍法が使えますね。local_search関数はTSPに対する局所探索法であれば何でも良いのですが、例えば前回の記事で登場した2-optによる局所探索法を採用しても良いでしょう。
ところで、GRASP法では初期解生成にランダム化グリーディ法を用いていますが、それに限らず何らの手法によって生成した初期解に対して局所探索法を適用することを反復する枠組みを多スタート局所探索法(multi-start local search, MLS法)と呼んだりします。GRASP法は多スタート局所探索法の一種というわけです。
...
それでは、これまでの記事で度々登場した48都市TSPの問題例に対してランダム化最近近傍法を用いたGRASP法を適用してみましょう。
今回の計算実験にあたって、GRASP法の終了条件はイテレーション10回としました。また、ランダム化最近近傍法において要素数$k$のnearest_setからランダムに次の移動先を選びますが、今回は$k=2$、つまり2都市のうちからランダムに選んで移動することとしました。さらに、最も近い都市に99%の確率で移動し、残り1%の確率で2番目に近い都市に移動することとしました。局所探索法には前回の記事で紹介した2-optによる局所探索法を利用しました。
比較のため、適用前の解として前回の記事で得られた結果(最近近傍法と2-optによる局所探索法)も載せています。使用した計算機はMacBook Pro(1.4 GHz クアッドコア Intel Core i5, 16 GB RAM)です。
48都市TSP
この問題例は最適値(すべての解の中で最も小さい総距離)が求められており、その総距離は10628です1。
適用前

総移動距離は11010であり、最適値に対しておよそ+3.6%の結果。計算時間は0.001秒(アルゴリズム自体は前回と変わっていませんが、今回の執筆にあたって時間計測まわりのコードの無駄を見直したため、前回の結果よりも短くなっています…)。
適用後
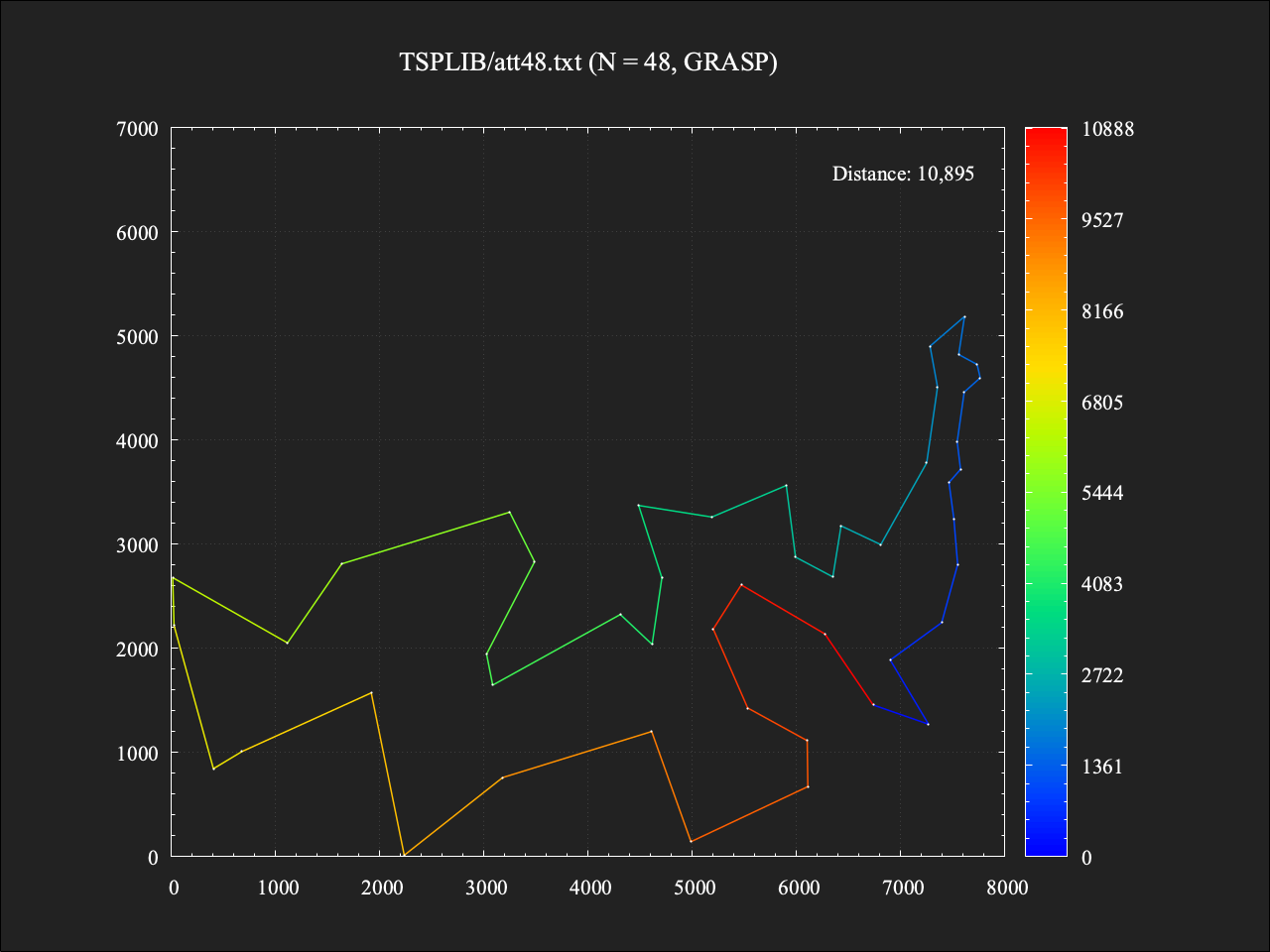
総移動距離は10895であり、最適値に対しておよそ+2.5%の結果。計算時間は0.013秒となり、適用前のおよそ10倍となったが、これは単純にGRASP法のイテレーション数を10としたためである。最適値からの差としては約1.1%改善できた。
...
さらに、いつもの1379都市TSPの問題例に対してもGRASP法を適用してみます。
1379都市TSP
この問題例も最適値が求められており、その総距離は56638です1。
適用前
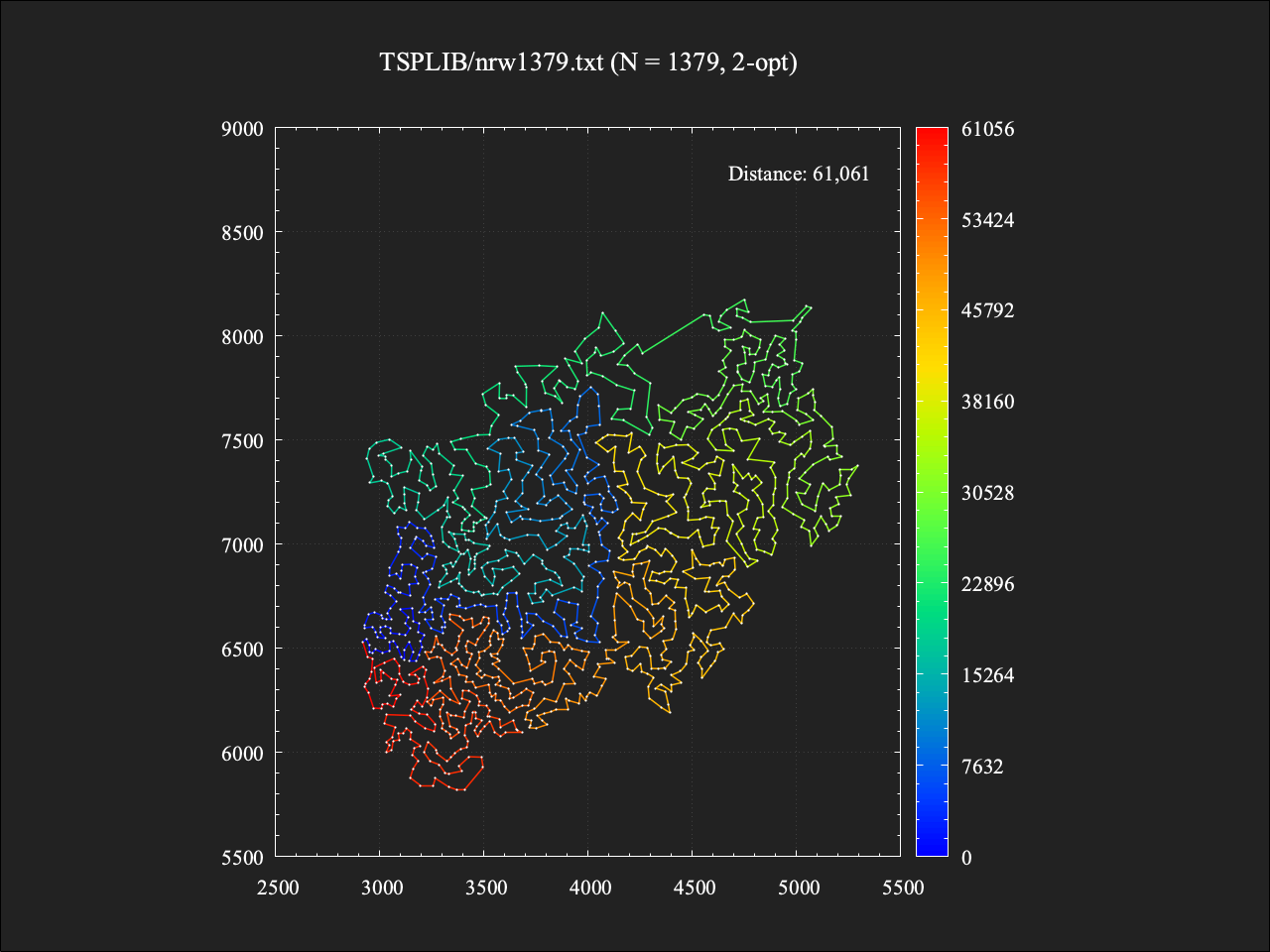
総移動距離は61061であり、最適値に対しておよそ+7.8%という結果。計算時間は約0.4秒であった。
適用後
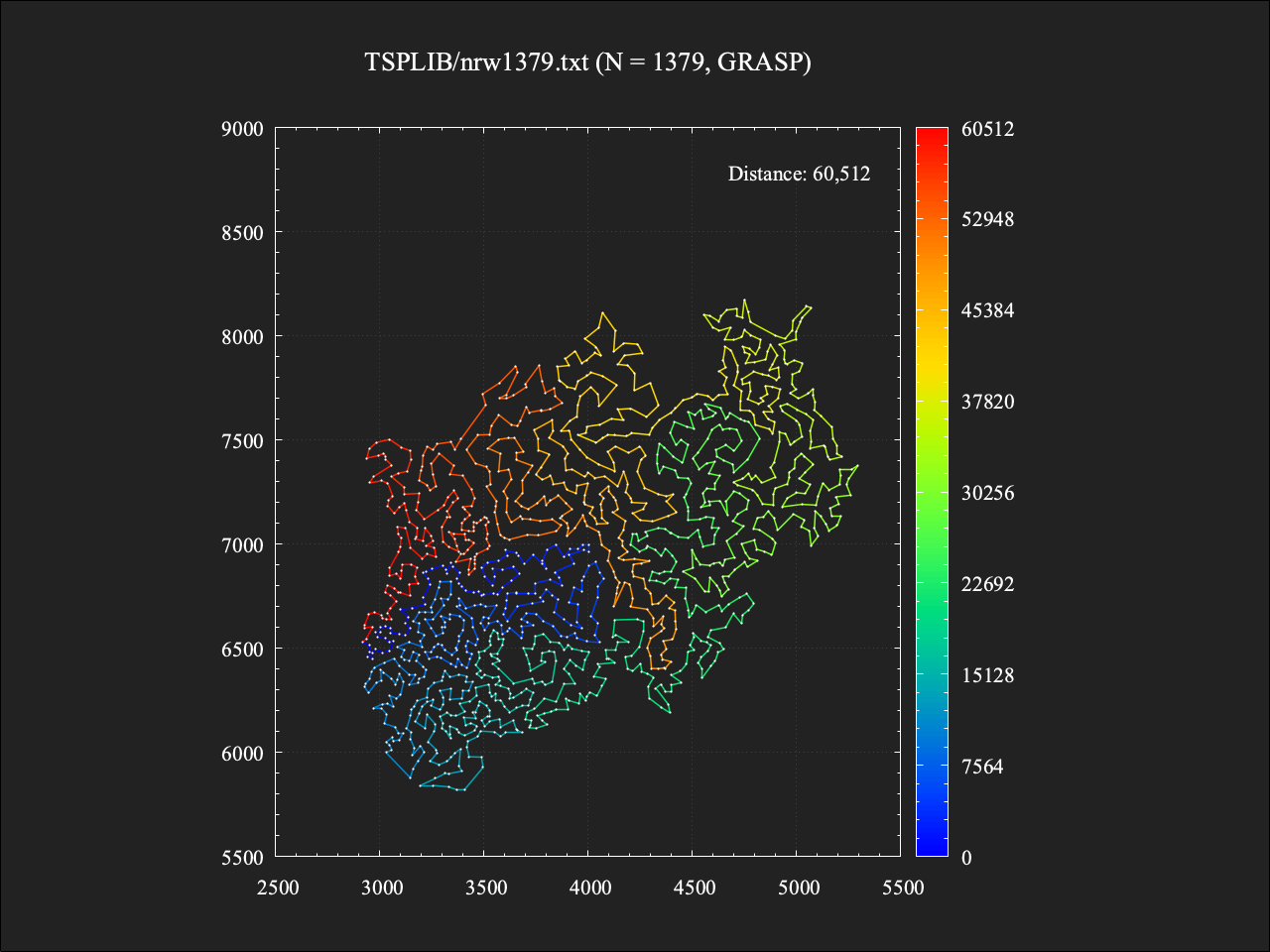
総移動距離は60512であり、最適値に対しておよそ+6.8%という結果。計算時間は約4.5秒であった。こちらも計算時間は約10倍となるものの、最適値からの差を1%改善できた。
これまでの手法の結果を比較
| att48 (10628) |
kroA100 (21282) |
tsp225 (3916) |
att532 (27686) |
nrw1379 (56638) |
|
|---|---|---|---|---|---|
| その1: 最近近傍法 | 12861 | 27807 | 5030 | 35516 | 68964 |
| その2: 局所探索法 (最近近傍法+2-opt) |
11010 | 22399 | 4304 | 29739 | 61061 |
| 今回: GRASP法 (ランダム化最近近傍法+2-opt) |
10895 | 21843 | 4158 | 29320 | 60512 |
これまでの連載で紹介してきた手法の結果を表にまとめてみました。att48とnrw1379はこれまで48都市TSP、1379都市TSPとして扱ってきた問題例です。問題例名の下の丸括弧は最適値を表しています。それぞれの手法で計算時間に差があることをはじめ、実装の任意性があったり、パラメータ調整で更に改善の余地があったりなどもするため、この結果から厳密にどれが一番とは言い難いですが、どの手法でもある程度現実的な時間内で解が得られているという意味では、ここまでのところ今回のGRASP法がざっくり性能高いかな、というところでしょうか。
...
まとめ
単純な局所探索法から発展させた多スタート局所探索法の一種であるGRASP法を用いることで、局所探索法のみの場合と比べて計算時間を犠牲にしつつも更に解を改善できることがわかりました。局所探索法のみの場合、最終的にある特定の局所最適解に陥ってしまい探索終了となるのみでしたが、GRASP法では多様な初期解から探索を始めることで、結果的に複数の局所最適解を比較・評価することが可能となるため、アルゴリズム全体として探索の多様性が増し、より良い結果が得られたのだと言えると思います。
次回は解の多様性をいかに広げるかに着目した手法の一つである反復局所探索法をご紹介できればと思います。
- ランダム化最近近傍法により、多様なTSPの初期解を生成できる
- GRASP法により、探索の多様性が増すことで計算時間を犠牲にしつつも解を更に改善できる
- 反復局所探索法と呼ばれる手法により、単純な局所探索法よりも解を改善出来る(次回)
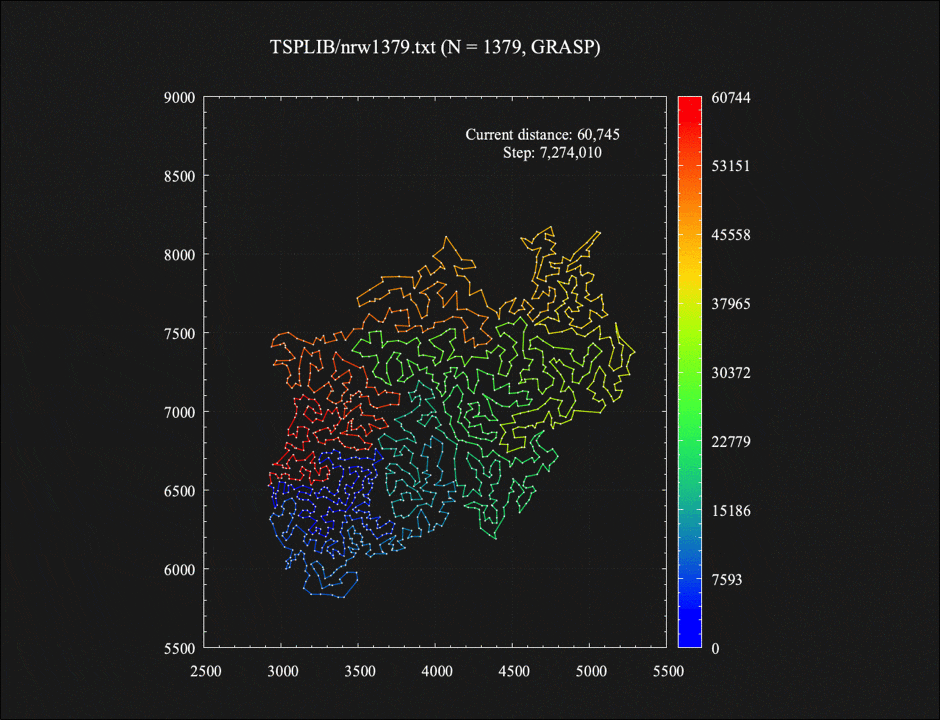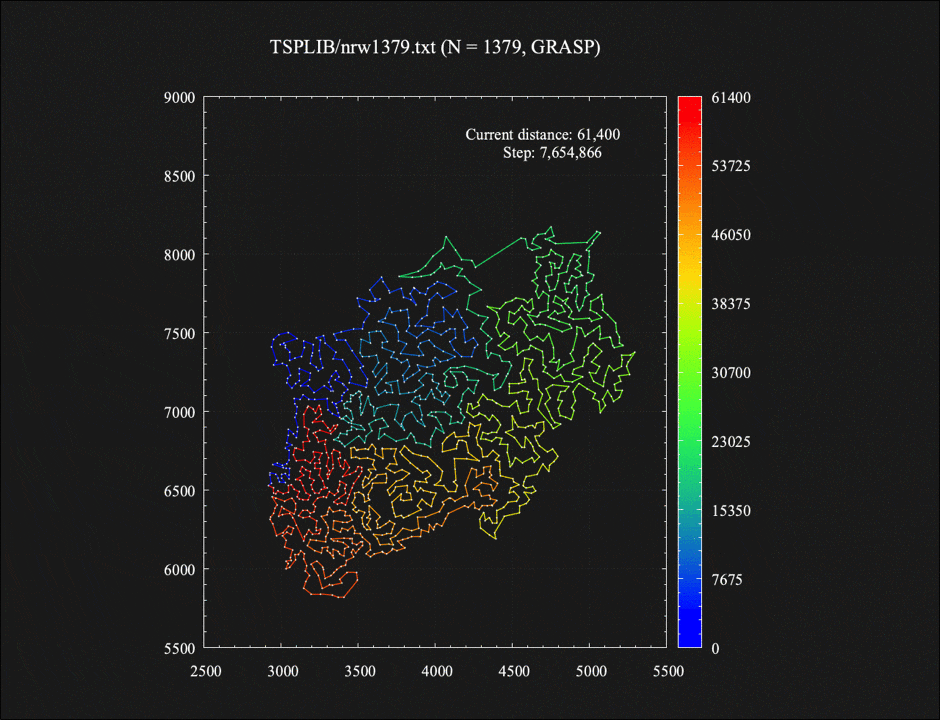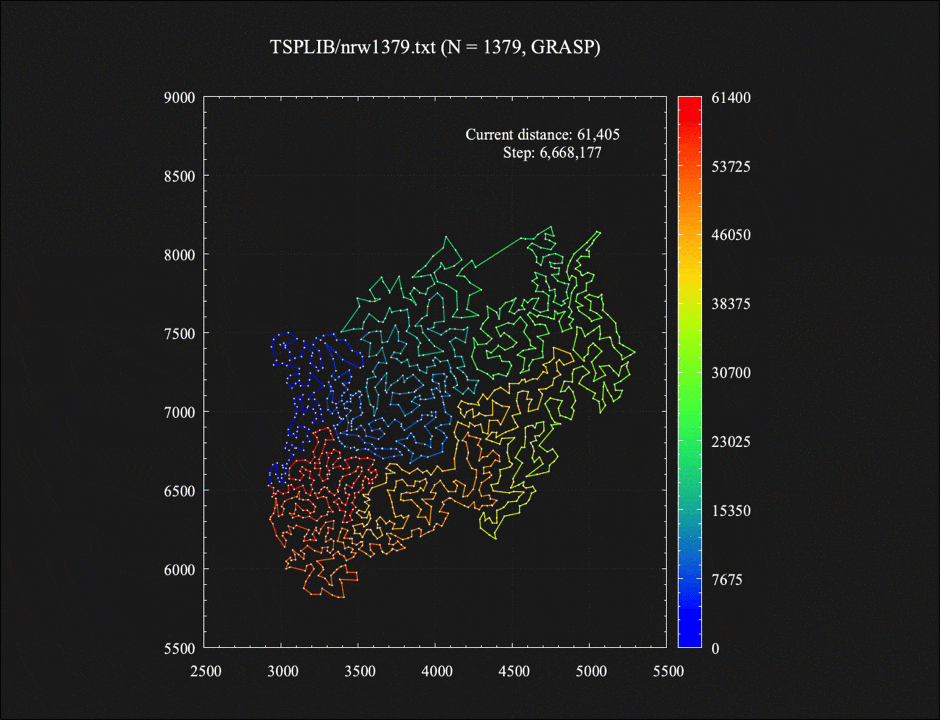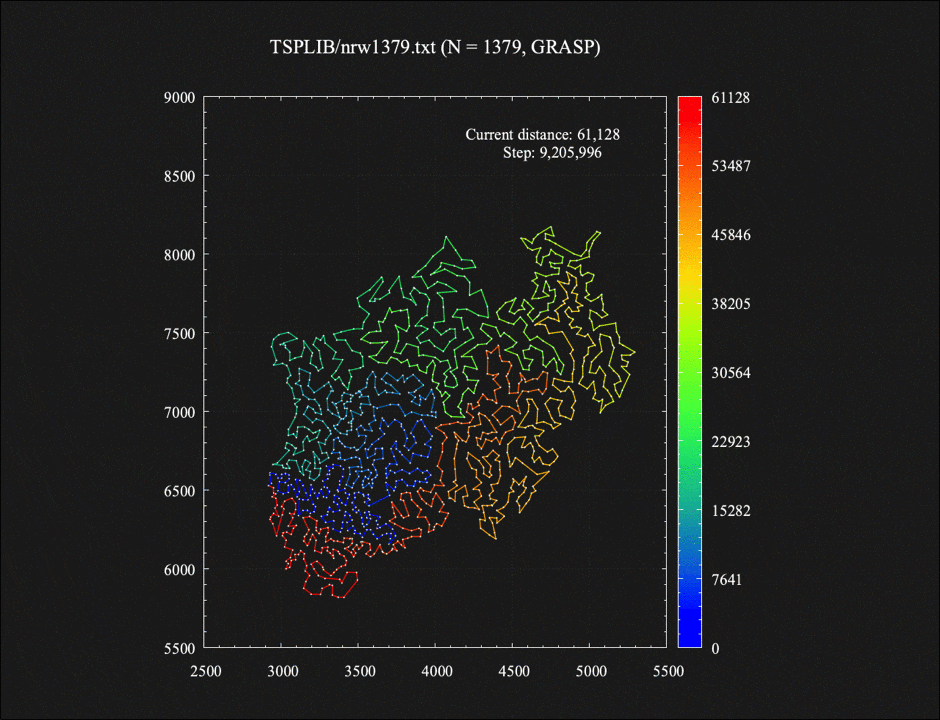
付録: 1379都市TSPに対するGRASP法の各イテレーション終了時に生成された解たち
GRASP法の各イテレーション終了時に生成された10個の解をつなげてコマ送りのアニメーションにしてみました。それぞれの解が(2-opt近傍における)局所最適解となっています。最近近傍法による初期解生成時、1%の確率で2番目に近い都市に移動する、という一見わずかなランダム性を加えただけなのに、最終的に得られる解としてはそれぞれ大きく異なってくるのが面白い気がします。
参考文献
柳浦睦憲 / 茨木俊秀 著、『組合せ最適化 -メタ戦略を中心として-』
T.A. Feo and M.G.C. Resende, "Greedy Randomized Adaptive Search Procedures," J. Global Optimization, vol.6, pp.109-133, 1995.
おわりに
ここまで読んでいただきありがとうございました。
株式会社オプティマインドでは、一緒に働く仲間を大募集中です。
カジュアル面談も大歓迎ですので、気軽にお声がけください。
【エンジニア領域の募集職種】
●ソフトウェアエンジニア
●QAエンジニア
●Androidアプリエンジニア
●組合せ最適化アルゴリズムエンジニア
●経路探索アルゴリズムエンジニア
●バックエンドエンジニア
●インフラエンジニア
●UXUIデザイナー
【ビジネス領域の募集職種】
●セールスコンサルタント
●上場準備担当
『Loogiaってどんなサービス?』については、こちら
Wantedlyでもこちらで募集中