本記事について
深層学習の基本である「回帰」を使って、
住宅価格を予測するプログラムを作ってみようと思います。
出来るだけ初心者目線で書いていきます。
前回記事はこちらです。
回帰ってなに?
回帰とは、特徴的なデータをもとに__数値を予測__するタスクのことを言います。
今回は住宅価格を予測するプログラムを作りますが、株やFX(外国為替取引)の値動きの予測も可能です。
import
インポートは↓です。
今回はデータの確認用にpandasをインポートしましょう。
ちなみに、pandasは非常に扱いやすいですが速度はとても遅いです。
学習の際にはnumpyを使い、目視確認やデータの前処理段階でpandasを使うのが一般的です。
from tensorflow.keras.datasets import boston_housing
from tensorflow.keras.layers import Activation, Dense, Dropout
from tensorflow.keras.models import Sequential
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.optimizers import Adam
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
住宅価格のダウンロード
今回、住宅価格を予測するにあたって、boston_housingというライブラリを使います。
boston_housingには、米国ボストンの住宅を決めるにあたっての特徴的な情報とその正解ラベルが入っています。
特徴的な情報(以下、説明変数)には、その地域の犯罪率とかアクセスの良さとかが入ってます。
当然ですが、この説明変数にいい加減な情報が入っていると、予測の精度が悪くなります。
例えば、周辺にあるパチンコ店の数を説明変数に加えても
パチンカーしか価値を感じないので、予測の邪魔になるでしょう。
万人が価値を感じるようなものを加えなければいけません。
回帰予測で最も難しいのはこの説明変数の定義なのですが、
今回はダウンロードしたデータに含まれるので楽ですね。
ダウンロードは以下のコードです。
ダウンロードした説明変数は正解ラベルを学習用と検証用で分けています。
(train_data, train_labels)が学習用で、(test_data, test_labels)が検証用です。
この辺は前回記事の分類と同じです。
(train_data, train_labels), (test_data, test_labels) = boston_housing.load_data()
shape数を確認します。
学習用データは404件、検証用データが102件。
前回記事の分類と比べてやたらと少ないですね。本当に予測できるのか不安になる件数です。

データの前処理
続いて、最も地味で最も重要な作業、データの前処理です。
今回の住宅価格の予測は時系列データではないので、連続性がありません。
そんなデータを予測する場合は、データをシャッフルしておいた方が無難です。
※株やFXなどの時系列データ予測の際にはシャッフルは厳禁です。
random.random()で乱数を作り、np.argsort()でインデックスを作ってソートします。
order = np.argsort(np.random.random(train_labels.shape))
train_data = train_data[order]
train_labels = train_labels[order]
続いて、住宅価格を決める説明変数を正規化します。
今回は正規化で説明変数を平均0の分散1の数値にします。
回帰予測では大きい数値の説明変数に予測が引っ張られることがあるため、
このように正規化しておくと良いと言われています。
正規化は、正規化したいデータから平均を引いて標準偏差で割ると算出できます。
コードは↓です。
mean = train_data.mean(axis=0)
std = train_data.std(axis=0)
train_data = (train_data - mean) / std
test_data = (test_data - mean) / std
pandasを使って、説明変数が正規化されていることを確認しましょう。
# データセットの前処理後のデータの確認
column_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
df = pd.DataFrame(train_data, columns=column_names)
df.head()

モデルの作成
ニューラルネットワークのモデルを作成します。
今回は全総結合の層を3つ用意します。
※今回はDropoutはありません
model = Sequential()
model.add(Dense(64, activation='relu', input_shape=(13,)))
model.add(Dense(64, activation='relu'))
model.add(Dense(1))
model.compile(loss='mse', optimizer=Adam(lr=0.001), metrics=['mae']) # コンパイル
1つ1つ解説します。
まず、model = Sequential()でシーケンシャルモデルを作成します。
model.add(Dense(64, activation='relu', input_shape=(13,)))は入力層です。
Dense:全総結合、ユニット数:64、活性化関数:ReLU、説明変数:13個
model.add(Dense(64, activation='relu'))は隠れ層です。
Dense:全総結合、ユニット数:64、活性化関数:ReLU
model.add(Dense(1))は出力層です。
今回は数値の予測なので、ユニット(出力数)は1つだけです。
モデルのコンパイル
model.compile(loss='mse', optimizer=Adam(lr=0.001), metrics=['mae'])でコンパイルします。
loss='mse'で予測値と実際の値の__誤差の求めるための損失関数__をセットします。
回帰に向いているといわれるmseをセットしましょう。
optimizer=Adam(lr=0.001)で__誤差を小さくするための最適化関数__にAdam、学習率は0.01をセットします。
metrics=['mae']で__モデルの性能を評価するための評価関数__のmaeをセットします。
学習
今回はEarlyStoppingを使って学習をしたいと思います。
EarlyStoppingを使うと、指定のエポック数で学習の改善が見られなかった場合、自動で止めてくれます。
今回は20エポックで改善が見られなかった場合、止めたいと思います。
学習は、最大エポック数を500、検証用データは2割にセット、callbacks=[early_stop]でEarlyStoppingを有効化します。
# EarlyStoppingを準備
early_stop = EarlyStopping(monitor='val_loss', patience=30)
# 学習の実行
history = model.fit(train_data, train_labels, epochs=500,
validation_split=0.2, callbacks=[early_stop])

学習状況の説明です。
__lossは訓練データの誤差__です。0に近いほど良い結果です。
__maeは訓練データの平均絶対誤差__です。0に近いほど良い結果です。
__val_lossは検証データの誤差__です。0に近いほど良い結果です。
__val_maeは検証データの平均絶対誤差__です。0に近いほど良い結果です。
エポック数を500でセットしていますが、途中で改善が見られなくなって打ち切られているかと思います。
学習結果をグラフで表示
学習結果が保存されているhistory.historyをmatplotlibで描画します。
plt.plot(history.history['mae'], label='train mae')
plt.plot(history.history['val_mae'], label='val mae')
plt.xlabel('epoch')
plt.ylabel('mae [1000$]')
plt.legend(loc='best')
plt.ylim([0,5])
plt.show()
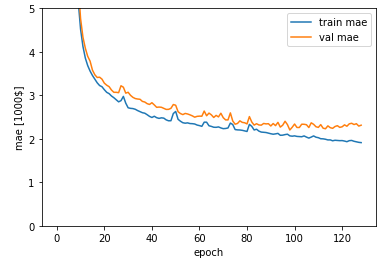
学習の評価
model.evaluteで学習データを評価します。
test_loss, test_mae = model.evaluate(test_data, test_labels)
print('loss:{:.3f}\nmae: {:.3f}'.format(test_loss, test_mae))

学習データより結果が悪いですが、概ね近い結果が出せました。
400件程度の少ない件数でもここまで近い数値が出せるのはすごいですね。
おそらく説明変数の定義が優秀なんでしょう。
推論
最後に予測データを出力して確認してみましょう。
最初に正解ラベルを表示して、そのあと推論します。
推論の出力結果は2次元なので、flatten()で1次元に変換しておきましょう。
# 正解ラベルを表示
print(np.round(test_labels[0:10]))
# 推論した値段の表示
test_predictions = model.predict(test_data[0:10]).flatten()
print(np.round(test_predictions))
 正解ラベルに近い数値が出せているようです。
正解ラベルに近い数値が出せているようです。
この予測値より下回っている物件は相場よりも安く売られている可能性があるということです。
ただ、説明変数で表現できない理由(幽霊が出る等)で安くなっている場合もあります。
この予測結果だけで売買をするのは危険ですが、参考にはなるかと思います。