本記事について
深層学習の基本である「分類」を使って、
手書きの数字文字が、なんの数字か予測するプログラムを作ってみようと思います。
出来るだけ初心者目線で書いていきます。
深層学習ってなに?
簡単に言いますと、大量のデータを使ってデータの規則性を見つける手法のことです。
以下の3プロセスから構成されています。
- モデル作成とコンパイル
- 学習
- 推論
深層学習の分類ってなに?
ざっくり言いますと、特徴的なデータをもとに__データの種類__を予測することです。
特徴的なデータというのは画像であったり、
直近の時系列データであったり、
予測をするためのヒントになるようなものです。
特徴量とか説明変数なんて言ったりもします。
「犬」と「猫」といった2種類のパターンを分類する場合は、__2クラス分類__といいます。
この場合の特徴量は大量の犬と猫の画像になると思います。
また、「晴れ」「曇り」「雨」といった3種類以上のパターンを分類をする場合は、__多クラス分類__といいます。
今回の記事では、0~9の手書き数字の画像を、実際の数値に分類(多クラス分類)してみます。
import
ライブラリはtensorflowを利用します。
tensorflowがなかったら、事前にpip installでインストールしておいてください。
ちなみに、今回、tensorflowのkerasというパッケージを利用するのですが、これは独立したkerasとは異なるパッケージです。
tensorflowのkeras ≠ 独立したkeras
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Activation, Dense, Dropout
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.utils import to_categorical
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
手書き数字データのダウンロード
手書きの数字を分類を予測するので、実際に手書き数字データを用意しなければなりません。
実際に手で書いて用意するというのもアリですが、面倒なのでMNISTというライブラリを利用してダウンロードしましょう。
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
MNISTでダウンロードしたデータを、以下の4種類のデータに分割します。
学習で使うための手書き数字のデータと、その答えが入ったラベルデータ:(train_images, train_labels)
テストで使うための手書き数字のデータと、その答えが入ったラベルデータ:(test_images, test_labels)
train_imagesというくらいだから、画像が入っているの?
と思うかもしれませんが、中身は配列です。
画像データを28行28列の配列で表現したものが大量に入っています↓
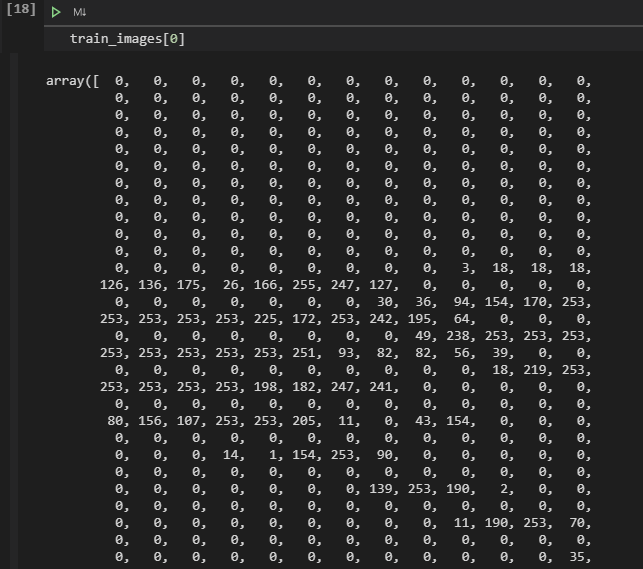
そして、train_labelsにはその画像の答えのデータが入ってます。
私の環境だと、train_labels[0]を中身を見ると、数字の5が入ってます。
これは、「train_images[0]の画像(配列)は5です」という意味になります。
(test_images, test_labels)も中身の構造は同じです。
test_images[0]の答えはtest_labels[0]に入っています。
この後の手順では、(train_images, train_labels)を使って学習して、
(test_images, test_labels)で正誤を確かめるという流れになります。
※一般的に、機械学習などで使う学習データをtrainと表現し、学習結果の確認に使うデータをtestと表現することが多いようです。
手書き数字データの確認
配列だと人間の目に優しくないので、
10個ほど画像に変換して確認します。
for i in range(10):
plt.subplot(1, 10, i+1)
plt.imshow(train_images[i], 'gray')
plt.show()
なにやら手書き数字っぽいものが入っていることが確認できました。
続いて、ラベルデータを確認します。
print(train_labels[0:10])
[5 0 4 1 9 2 1 3 1 4]が出力されます。
ちゃんと手書き数字の画像と一致しているようです。
データセットの前処理
データの読み込みは終わりましたが、このままでは予測は出来ません。
予測が出来るように画像の配列データと答えのラベルデータを整形したいと思います。
これをデータの前処理といい、とても重要な作業です。
とある現役データサイエンティストさんのブログを見ると、
AI作成作業よりも前処理の作業が大半を占めていると書かれていました。
現在のimagesに入っている各画像は28行28列の2次元配列になっています↓
これを、reshapeを使って1次元の配列に直します↓
(28×28=784だから784)
train_images = train_images.reshape((train_images.shape[0], 784))
test_images = test_images.reshape((test_images.shape[0], 784))
続いて、ラベルデータの整形処理です。
ラベルデータは、「One-Hot表現」に変換します。
「One-Hot表現」とは、ある要素のみが1で他が0になる表現方法です。
答えが「5」だった場合、以下のような表現方法になります。
[0,0,0,0,1,0,0,0,0] #5番目に1が入る
to_categoricalを使って直します↓
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
これでデータの前処理は完了です。
モデルの作成
前処理が終わったので、次はモデルを作成します。
モデルというのは、簡単に言いますと設計図のようなものです。
入力層の数、隠れ層の数、Dropoutの無効化率、出力層の数、なんの活性化関数を使うかなどを宣言します。
model = Sequential()
model.add(Dense(256, activation='sigmoid', input_shape=(784,))) # 入力層
model.add(Dense(128, activation='sigmoid')) # 隠れ層
model.add(Dropout(rate=0.5)) # ドロップアウト
model.add(Dense(10, activation='softmax')) # 出力層
1つ1つ解説します。
モデルの宣言
model = Sequential()でSequentialモデルを作成しています。
Sequential(シーケンシャル)は、層がいくつも重なっているような構造体のモデルです。
ケーキのミルフィーユを想像すると良いかもしれません。
入力層
model.add(Dense(256, activation='sigmoid', input_shape=(784,)))が入力層です。
Denseは全結合層を表します。全結合層とは、すべてのユニットを次の層に繋げるという意味です。
今回は256のユニットを作成しています。
activation='sigmoid'は、利用する活性化関数です。
sigmoidと書くことで、活性化関数にシグモイド関数を利用できます。
活性化関数を使うことで、線形分離が難しい複雑なデータでも特徴を捉えることが可能になります。
input_shape=(784,)は、入ってくるデータの数です。
隠れ層
model.add(Dense(128, activation='sigmoid'))は隠れ層です。
隠れ層があることで、複雑な特徴を捉えることが可能になります。
隠れ層はいくらでも増やせるのですが、
やりすぎると学習データでしか通用しない分類予測のモデルが出来てしまいます。
「過学習」や「カーブフィッティング」などと言ったりします。
ドロップアウト
model.add(Dropout(rate=0.5))はドロップアウトです。
ドロップアウトは過学習を防ぐために、一部のユニットを無効にする手法です。
rateで無効化率を定めます。一般的に50%を無効化にすると良いと言われています。
ただ、必ずしも実行しなければいけないというものでも無いようです。
出力層
model.add(Dense(10, activation='softmax'))は出力層です。
今回は0~9の10種類の多クラス分類になるので、ユニット数は10になります。
また、活性化関数にはソフトMAX関数を利用しています。
ソフトMAX関数は、分類の合計値が1になるのような多クラス分類に向いていると言われています。
今回はsigmoidとsoftmaxしか使っていませんが、他にも色々な活性化関数があるそうです。
モデルのコンパイル
次に作成したモデルのコンパイルを行います。
以下の1行で終わりですが、重要な情報が詰まってます。
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=0.1), metrics=['acc'])
コンパイルには以下の3つを設定する必要があります。
- 損失関数
- 最適化関数
- 評価指標
損失関数とは
モデルの予測値と正解データの__誤差__を計算する関数です。
多クラス分類では、categorical_crossentropy(多クラス交差エントロピー誤差)という関数がよく使われます。
loss='categorical_crossentropy'でセットしましょう。
最適化関数とは
損失関数で計算した誤差が0に近づくよう重みとバイアスを調整してくれる関数です。
SGDやAdamという最適化関数が代表的です。
今回はSGDを使います。SGDの引数であるlrは学習率を表します。
各層の重みをどの程度の頻度で更新するかを決める値です。今回は0.1を設定します。
optimizer=SGD(lr=0.1)
評価指数とは
モデルの性能を測定するための指標です。
主な評価指標として、accやmseなどがあります。
分類でよく利用されるのは正解率を表すacc(Accuracy)です。
回帰などの数値を予測する場合は、mseが良いとされています。
metrics=['acc']
学習
ようやく準備が整ったので学習しましょう。
train_imegesとtrain_labelsを使って学習します。
学習はmodel.fitで行います。
history = model.fit(train_images, train_labels, batch_size=500,
epochs=5, validation_split=0.2)
batch_sizeというのは訓練データをいくつの単位で訓練に利用するかの設定です。
大きくなればなるほど学習速度は速くなりますが、メモリを消費します。
epochsは訓練するエポック数です。
validation_splitは訓練データと検証データを分ける割合です。
0.2だと検証データに2割利用することになります。
実行すると↓のような感じになります。
各エポックでの学習状況が記載されていきます。
これを見ると「すごい!AIを作ってる!」という気がしてとてもワクワクしてきます。
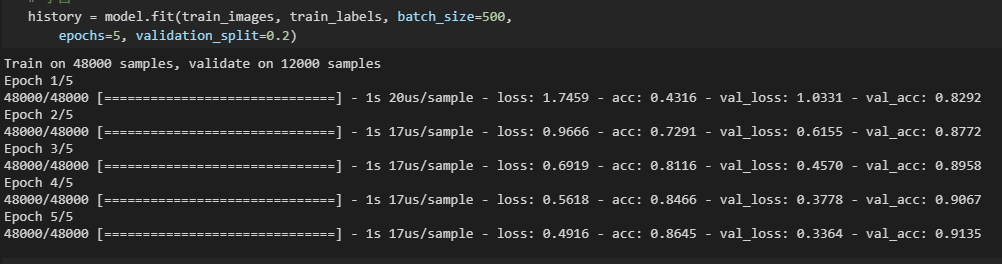
学習状況の説明です。
lossは__訓練データの誤差__です。0に近いほど良い結果です。
accは__訓練データの正解率__です。1に近いほど良い結果です。
val_lossは__検証データの誤差__です。0に近いほど良い結果です。
val_accは__検証データの正解率__です。1に近いほど良い結果です。
エポック数を増やし過ぎて過学習になると、
lossとaccはすごくいい数値なのに
val_loss,val_accが悪い数値になります。
ようは__過去問やりすぎて過去問しか解けないバカ__になってしまうのです。
エポック数はほどほどの数値にセットしましょう。
ちなみに、学習結果はhistory.historyで確認できます。
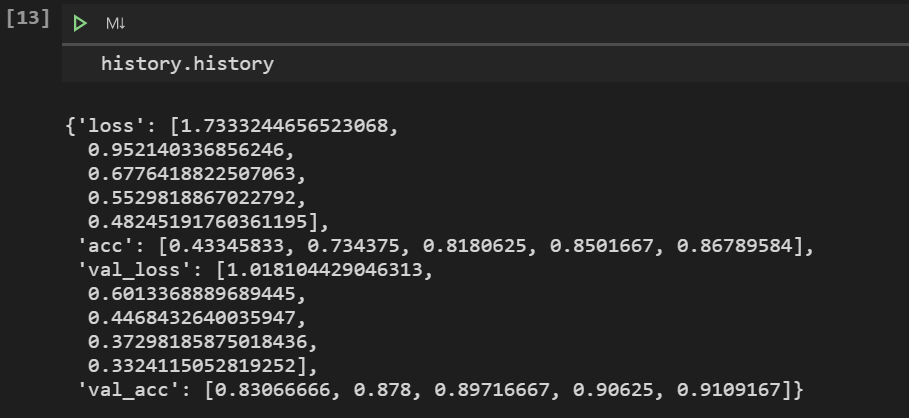
グラフ表示する場合は以下のコードです。
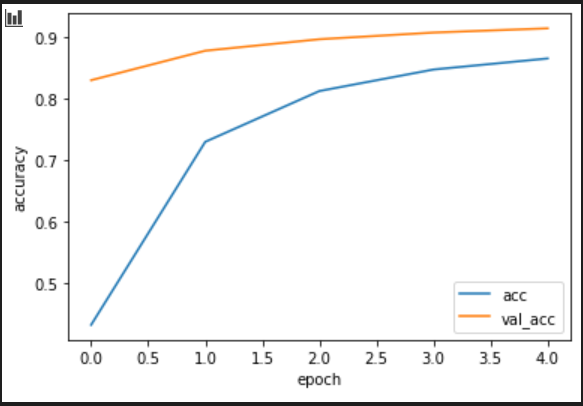
plt.plot(history.history['acc'], label='acc')
plt.plot(history.history['val_acc'], label='val_acc')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(loc='best')
plt.show()
学習結果の評価
学習が完了したら、テストデータを使って評価を行います。
評価はmodel.evaluateを使います。
test_loss, test_acc = model.evaluate(test_images, test_labels)
print('loss: {:.3f}\nacc: {:.3f}'.format(test_loss, test_acc ))
推論
最後に、実データをもとに推論を行います。
これにより、予測した個別の結果が取得できます。
推論する画像の表示します↓
for i in range(10):
plt.subplot(1, 10, i+1)
plt.imshow(test_images[i].reshape((28, 28)), 'gray')
plt.show()

この画像を、model.predictに入れて、推論を行います。
np.argmaxでその結果を取り出すことができます。
test_predictions = model.predict(test_images[0:10])
test_predictions = np.argmax(test_predictions, axis=1)
print(test_predictions)
出力結果は以下のようになりました。
[7 2 1 0 4 1 4 9 6 9]
すべて正解したようです。
実際にAIとして運用する場合はtest_imagesではなく、
予測したいデータをmodel.predictに放り込んで予測します。
modelを保存しておけば、再度の学習は不要です。
長くなりましたが、以上になります。

