はじめに
本記事は全4回の連載のうちの第3回です.
前回の記事はこちら.
AlphaGoを模したオセロAIを作る(2): RLポリシーネットワーク - Qiita
また, ソースコードの全文はこちらにあります.
前の2回で作ったSLポリシーネットワークとRLネットワークを使って対戦結果を大量に生成して, 盤面の評価値を決める関数を作っていきます.
SLポリシーネットワークの対象が, 盤面から打つ場所を選択する分類問題であったのに対し, バリューネットワークの対象は盤面から勝てる見込みを算出する回帰問題となります.
教師データ生成
バリューネットワークに読ませる教師データを用意します.
盤面と勝敗(勝ち/負け/引き分けを+1/-1/0とする)の組合せがたくさんあればいいのですが, 同じゲームから複数の盤面と勝敗のセットを取り出すと独立性が損なわれるので, 1ゲームからは1セットのみを取り出すこととします.
アルファ碁を参考に, 次のような手順でデータを生成しました.
- 4から63までの間でランダムに数字$N$を選ぶ
- 石が$N$個になるまでSLポリシーネットワークどうしでゲームを進める
- この時の盤面を保存する
- 合法手の中からランダムに選んだ場所に石を置く
- RLポリシーネットワークどうしで終局までゲームを進める
- 勝敗を保存する
これを約125万回繰り返し, 反転・回転対称性を利用して8倍にデータを拡張して約1000万組のデータセットを得ました.
(複数のマシンを使っても1日以上かかりました. 後日ゲームのアルゴリズムを改良したいです)
自己対戦を行うためのコードがこちらです.
class SelfPlay:
def __init__(self, stop_num):
# 盤面の初期化
self.state = np.zeros([8, 8], dtype=np.float32)
self.state[4, 3] = 1
self.state[3, 4] = 1
self.state[3, 3] = 2
self.state[4, 4] = 2
# ゲーム内変数の初期化
self.stop_num = stop_num # 乱数N
self.stone_num = 4
self.pass_flg = False
# モデルをセット
self.model0 = L.Classifier(SLPolicy.SLPolicyNet(), lossfun=softmax_cross_entropy)
serializers.load_npz("./models/sl_model.npz", self.model0)
self.model1 = L.Classifier(SLPolicy.SLPolicyNet(), lossfun=softmax_cross_entropy)
serializers.load_npz("./models/rl_model.npz", self.model1)
# 呼び出されたら盤面と勝敗を返す
def __call__(self):
# SLポリシーネットワークで自己対戦
cl = 1
while(self.stone_num<self.stop_num):
self.turn(cl, self.model0)
cl = order(cl)
# ここで盤面を保存
color = cl
state = copy.deepcopy(self.state)
if color==1:
# AI1's turn
tmp = 3*np.ones([8,8], dtype=np.float32)
state = state*(tmp-state)*(tmp-state)/2
# ランダムに置く
positions = self.valid_pos(cl)
if len(positions)==0:
return state, -1
position = random.choice(positions)
self.place_stone(position, cl)
self.pass_flg = False
self.stone_num += 1
cl = order(cl)
# RLポリシーネットワークで自己対戦
while(self.stone_num<64):
self.turn(cl, self.model1)
cl = order(cl)
return state, self.judge(color)
自己対戦を実行して盤面と勝敗をtxtファイルに書き出すコードがこちらです.
import argparse
import numpy as np
from tqdm import tqdm
import value_self_play
def main():
parser = argparse.ArgumentParser(description='IaGo:')
parser.add_argument('--size', '-s', type=int, default=1250000, help='Number of games to play')
args = parser.parse_args()
for i in tqdm(range(args.size)):
rand = np.random.randint(4,64)
self_play = value_self_play.SelfPlay(rand)
state, result = self_play()
with open("./value_data.txt", "a") as f:
f.write(str(state) + "\n")
f.write(str(result) + "\n")
if __name__ == '__main__':
main()
終わったら, 第1回を参考に, テキストファイルを読み込み, 8倍に拡張してからnpy形式で保存してください.
私はshapeが1000万88のstates.npy, 1000万のresults.npy, 100088のstates_test.npy, 1000のresults_test.npyを作りました.
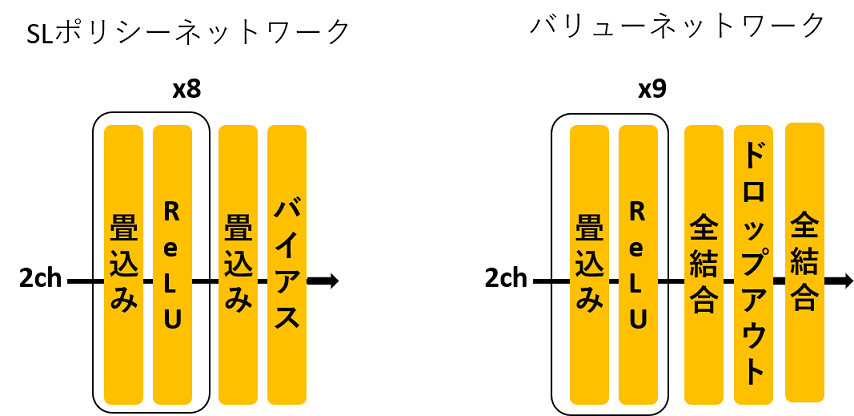
モデル構築
ネットワーク構造はSLポリシーネットワークとほぼ同じですが, 回帰問題なので最後に全結合層とドロップアウトを加えました.
import chainer
import chainer.functions as F
import chainer.links as L
from SLPolicy import Block
class ValueNet(chainer.Chain):
def __init__(self):
ksize = 3
super(ValueNet, self).__init__()
with self.init_scope():
self.block1 = Block(64, ksize)
self.block2 = Block(128, ksize)
self.block3 = Block(128, ksize)
self.block4 = Block(128, ksize)
self.block5 = Block(128, ksize)
self.block6 = Block(128, ksize)
self.block7 = Block(128, ksize)
self.block8 = Block(128, ksize)
self.block9 = Block(1, ksize)
self.fc10 = L.Linear(None, 128, nobias=True)
self.fc11 = L.Linear(None, 1, nobias=True)
def __call__(self, x):
h = self.block1(x)
h = self.block2(h)
h = self.block3(h)
h = self.block4(h)
h = self.block5(h)
h = self.block6(h)
h = self.block7(h)
h = self.block8(h)
h = self.block9(h)
h = self.fc10(h)
h = F.dropout(h, 0.4)
h = self.fc11(h).reshape(-1)
return h
学習
損失関数を平均二乗誤差として学習させました.
学習ループもSLポリシーネットワークとほぼ同じです.
import argparse
import numpy as np
from tqdm import tqdm
import chainer
import chainer.links as L
from chainer import serializers, cuda, optimizers, Variable
from chainer.functions import mean_squared_error
import value
def main():
# エポック数とGPU IDの指定
parser = argparse.ArgumentParser(description='IaGo:')
parser.add_argument('--epoch', '-e', type=int, default=10, help='Number of sweeps over the dataset to train')
parser.add_argument('--gpuid', '-g', type=int, default=0, help='GPU ID to be used')
args = parser.parse_args()
# モデル定義
model = value.ValueNet()
optimizer = optimizers.Adam()
optimizer.setup(model)
optimizer.add_hook(chainer.optimizer_hooks.WeightDecay(5e-4))
cuda.get_device(args.gpuid).use()
# データ読み込み
test_x = np.load('./value_data/npy/states_test.npy')
test_y = np.load('./value_data/npy/results_test.npy')
test_x = np.stack([test_x==1, test_x==2], axis=0).astype(np.float32)
test_x = chainer.Variable(cuda.to_gpu(test_x.transpose(1,0,2,3)))
test_y = chainer.Variable(cuda.to_gpu(test_y.astype(np.float32)))
train_x = np.load('./value_data/npy/states.npy')
train_y = np.load('./value_data/npy/results.npy')
train_size = train_y.shape[0]
minibatch_size = 4096 # 2**12
for epoch in tqdm(range(args.epoch)):
model.to_gpu(args.gpuid)
# 損失関数が変化しない場合はコメントを外す
# chainer.config.train = True
# chainer.config.enable_backprop = True
# データをシャッフル
rands = np.random.choice(train_size, train_size, replace=False)
train_x = train_x[rands,:,:]
train_y = train_y[rands]
for idx in tqdm(range(0, train_size, minibatch_size)):
x = train_x[idx:min(idx+minibatch_size, train_size), :, :]
x = np.stack([x==1, x==2], axis=0).astype(np.float32)
x = chainer.Variable(cuda.to_gpu(x.transpose(1,0,2,3)))
y = train_y[idx:min(idx+minibatch_size, train_size)]
y = chainer.Variable(cuda.to_gpu(y.astype(np.float32)))
train_pred = model(x)
train_loss = mean_squared_error(train_pred, y)
model.cleargrads()
train_loss.backward()
optimizer.update()
# 損失関数の計算
with chainer.using_config('train', False):
with chainer.using_config('enable_backprop', False):
test_pred = model(test_x)
test_loss = mean_squared_error(test_pred, test_y)
print('\nepoch :', epoch, ' loss :', test_loss)
# ログ
with open("./log_value.txt", "a") as f:
f.write(str(test_loss)[9:15]+", \n")
# モデル保存
model.to_cpu()
serializers.save_npz('./models/value_model.npz', model)
serializers.save_npz('./models/value_optimizer.npz', optimizer)
if __name__ == '__main__':
main()
学習曲線を見てみると, 10エポック付近で底を打ってしまいました.

結果
実際に適当なデータを入力して結果を見てみましょう.
AIは白(プレイヤー2)なので, 白が勝ちそうなときは+1に近い値を, 負けそうなときは-1に近い値を出すはずです.
適当な例で入力してみましたが, 概ね正しく予測できていると思われます.
これで時間のかかるディープラーニングは終わりです!
次回はモンテカルロ木探索を実装して, SLポリシーネットワークとバリューネットワークを組み合わせます.
AlphaGoを模したオセロAIを作る(4): モンテカルロ木探索 - Qiita
参考文献
[1] D. Silver et al., "Mastering the game of Go with deep neural networks and tree search," nature, Vol. 529, No. 7587, pp. 484-489, 2016.
DeepMindによるAlphaGoの論文です.
[2] 大槻知史, 三宅陽一郎, 『最強囲碁AI アルファ碁 解体新書 深層学習, モンテカルロ木探索, 強化学習から見たその仕組み』, 翔泳社, 2017.
原著論文[1]の解説書です. 非常にわかりやすかったです.
