AlphaGoを模したオセロAIを作る(1): SLポリシーネットワーク

はじめに

研究で，ある探索問題を解くためにAlphaGoの勉強をしています．
学んだアルゴリズムを自分で実装をしようと思ったのですが，囲碁だととてつもない計算資源が必要になるので，スケールを落としてオセロで試してみました．
本記事では，ChainerでAlphaGoのSLポリシーネットワークを実装し，ターミナル上でプレイできるようにします．
今のところ，このAI(IaGoという名前を付けました)は先読みを一切していませんが，結構強いです．
今後，強化学習やモンテカルロ木探索も実装していくつもりです．ご期待ください！
2018年8月23日追記: 全記事公開しました.

AlphaGoの背景

囲碁の難しさは第一に，そのパターンの多さにあります．探索空間の広さは$10^{360}$と言われており，表のとおり他のゲームよりも広いことがわかります．

ゲーム	探索空間の広さ	AIが人間に勝った年	AI	対戦した人
オセロ	$10^{60}$	1997	NEC Logistello	世界チャンピオン 村上健
チェス	$10^{120}$	1997	IBM Deep Blue	世界チャンピオン Garry Kasparov
将棋	$10^{220}$	2013	東京大学 GPS将棋	三浦弘行 八段
囲碁	$10^{360}$	2016	DeepMind AlphaGo	李世乭 九段

$10^{360}$というと，もう「億」や「兆」のような名前すらない規模でイメージもできませんが，観測可能な宇宙に存在する原子の総数と言われている$10^{80}$よりもずっと大きいのですから驚異的です．
ちなみに，情報の世界では「天文学的数字」よりも大きい数字がしばしば出てくるので，「組合せ論的数字」なんて言い方も耳にすることがあります．
この膨大なパターン数が原因で，AlphaGoが開発されるまでは「AIが囲碁で人間に勝利するまであと10年はかかる」と言われていましたが，2016年にディープラーニングを応用したAlphaGoが李世乭九段を破り世界を驚かせました．

AlphaGoのすごさを感じていただけたでしょうか？でも，$10^{360}$の世界で戦う人間の棋士もすごいですよね．
ともあれ，囲碁は難しいので私はオセロにしました．

必要なもの

ディープラーニングの基礎とChainerの基本的な使い方に関する知識を前提とします．
訓練から試す場合はGPUが無いと厳しいと思います．

完成したAIと対戦してみる

IaGoという名前をつけてソースコードを公開しています．
ターミナルで次のコマンドを順に実行すればゲームが始まります．詳しくはリンク先のREADMEを読んでください．

$ pip install chainer
$ git clone [e-mail]:shionhonda/IaGo.git
$ python ./IaGo/game.py

*Iago: Shakespear『オセロ』の登場人物

AlphaGoの全体像

AlphaGoで用いられているアルゴリズムは，SLポリシーネットワーク，RLポリシーネットワーク，バリューネットワーク，モンテカルロ木探索の4つに分けることができます．

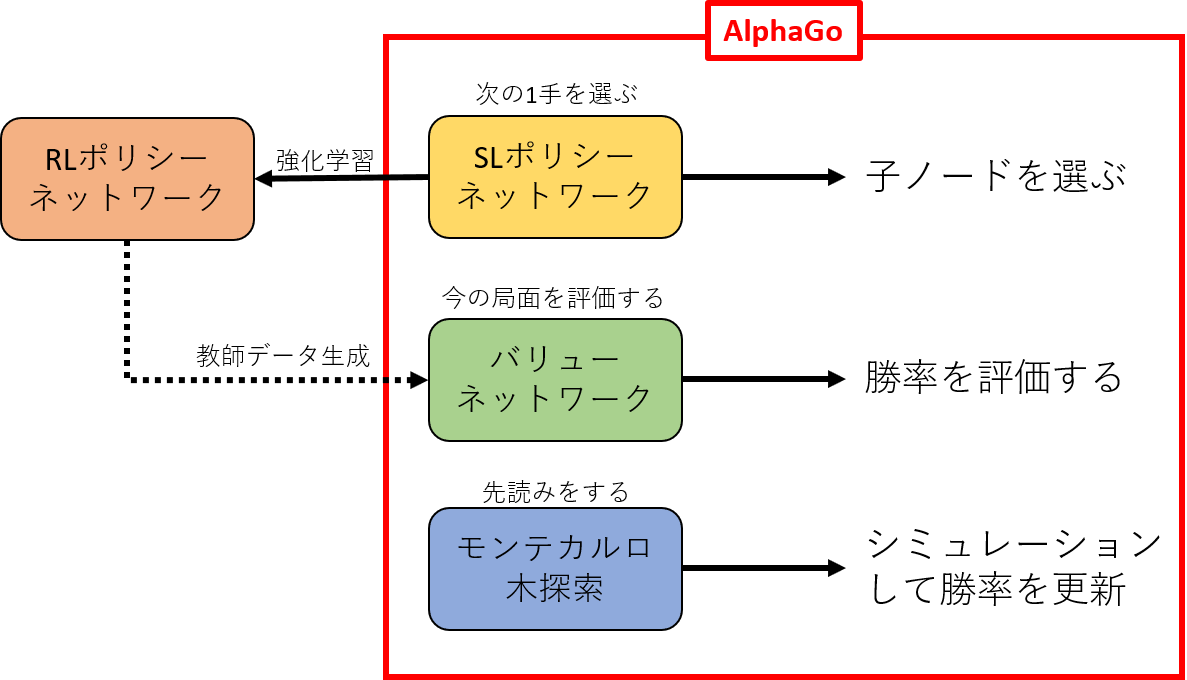
SLポリシーネットワーク

畳込みニューラルネットワーク(CNN; convolutional neural network)によって，ある局面から最適な次の一手を選択します．先読みはしません．
今回実装したのはこのSLポリシーネットワークです．
なお，AlphaGoでは，SLポリシーネットワークを単純化・高速化したロールアウトポリシーというものを用意して，モンテカルロ木探索のプレイアウトに使っています．
*SLは教師あり学習(supervised learning)の略

RLポリシーネットワーク

SLポリシーネットワークを元にして，自己対戦による強化学習でパラメータを調整したものです．
自己対戦の勝敗を報酬としてフィードバックを与えてあるので，極めて近視眼的なSLポリシーネットワークに「ゲームの勝敗」という大局的視点が加わっています．
バリューネットワークの教師データ生成に使いますが，AlphaGoそのものには使いません．
*RLは強化学習(reinforcement learning)の略

こちらは第2回で取り上げます．
AlphaGoを模したオセロAIを作る(2): RLポリシーネットワーク - Qiita

バリューネットワーク

ある局面から「勝てる見込み」を算出する評価関数です．
まず，入力された局面からRLポリシーネットワークによるプレイアウト(自己対戦を終局まで行うこと)を繰り返し，局面と勝率のデータセットを作ります．
このデータセットをCNNで学習し，局面から勝率を出力するネットワークを作ります．

こちらは第3回で取り上げます．
AlphaGoを模したオセロAIを作る(3): バリューポリシーネットワーク - Qiita

モンテカルロ木探索

囲碁やオセロを上手にプレイするには，「自分が次Aに打ったら盤面がこうなって，そうすると相手はBかCに打って…」と先読みすることが必要です．
しかし，囲碁では探索空間が膨大なので，全ての可能性を探索することは現実的な時間では不可能です．
この問題を解決するのがモンテカルロ木探索で，バリューネットワークにより局面の勝率を評価しながら，勝率の高い局面は深く探索し，勝率の低い局面をなるべく探索しないというアルゴリズムです．
こちらは第4回で取り上げます．
AlphaGoを模したオセロAIを作る(4): モンテカルロ木探索 - Qiita

データの用意

それではIaGoの実装に入ります．
まずはデータを用意しましょう．

データ取得

約23万対局分のオンラインオセロの棋譜がこちらで公開されています．
が，そのうち勝った方だけのデータをtxtファイルにまとめてくださった方がいるので，以下のリンク先で入手しdata.txtとして保存してください．
オセロの教師データ公開【ディープラーニング】 - Deeplearning とか 人工知能とか

データ読込み

リンクの説明に従って，「盤面」と「石を置く位置」の配列を作成します．

load.py

# data.txtを１行ずつ展開してstate(盤面)とaction(石を置く場所)を返す
def transform(string):
    flat = string.replace("\n", "").split(" ")
    state = np.array([int(flat[j]) for j in range(64)]).reshape(8,8)
    action = (int(flat[65])-1)*8 + int(flat[64])-1
    return state, action

def main():
    print("Loading data... (it might take a few minutes)")
    with open("../policy_data/txt/data.txt", "r") as f:
        data = f.readlines()

    # 白黒分けて保存する
    B_data = [] # 黒
    W_data = [] # 白
    for line in data:
        if 'B' in line:
            B_data.append(line)
        elif 'W' in line:
            W_data.append(line)
    len_B = len(B_data)
    len_W = len(W_data)

    # listをndarrayに変換
    states = np.zeros([len_B+len_W, 8, 8]) # 盤面
    actions = np.zeros(len_B+len_W) # 石を置く位置
    for i in range(0, len_B):
        states[i,:,:], actions[i] = transform(B_data[i])
    for i in range(len_B, len_B+len_W):
        st, actions[i] = transform(W_data[i-len_B])
        # 白の手は黒の手として読み込む(AIは黒番)
        st[np.where(st==0)] = 3
        states[i,:,:] = 3-st
    del B_data, W_data # メモリ解放
    '''後略'''

このAIは白番で後手なので逆になっていることに気づきましたが，おそらく大きな影響はないでしょう．
2018年8月14日追記: 元データと数字の割り当てを逆にしているので問題ありませんでした．

データ拡張

stateとactionの組が約607万セットできました．3GBくらいになると思います．
ここで，オセロの盤を90度回転・反転することによりデータを8倍に拡張することができます．メモリに余裕のある方は欲張ってみましょう．
stateの回転と転置はnumpyの組込み関数で簡単にできるので，actionが示す座標を回転・転置する関数を作ります．
rotate関数の式の導出は省略しますが，回転行列と平行移動の組合せです(高校数学を思い出しましょう！)．

load.py

# 反時計回りに90度回転
# actionは0-63の数字で盤上の位置を表す
# 回転するときは，中心が原点，左上のマスが(-3.5, -3.5)になるように軸をずらす
def rotate(action):
    y, x = action//8-3.5, action%8-3.5
    y_, x_ = -x+3.5, y+3.5
    return y_*8+x_

# 転置
# 転置するときは，中心が原点，左上のマスが(-3.5, -3.5)になるように軸をずらす
def transpose(action):
    y, x = action//8-3.5, action%8-3.5
    y_, x_ = x+3.5, y+3.5
    return y_*8+x_

これらの関数をmain関数に追加します．

load.py

def main():
    with open("../policy_data/txt/data.txt", "r") as f:
    '''中略'''
    del B_data, W_data #メモリ解放

    print("Augmenting data... (it might take a few minutes)")
    S = states # 拡張した盤面
    A = actions # 拡張した位置
    # 90度回転を3回
    for i in range(3):
        states = np.rot90(states, k=1, axes=(1,2))
        S = np.concatenate([S, states], axis=0)
        actions = rotate(actions)
        A = np.concatenate([A, actions], axis=0)
    # 転置
    states = states.transpose(0,2,1)
    S = np.concatenate([S, states], axis=0)
    actions = transpose(actions)
    A = np.concatenate([A, actions], axis=0)
    # 90度回転を3回
    for i in range(3):
        states = np.rot90(states, k=1, axes=(1,2))
        S = np.concatenate([S, states], axis=0)
        actions = rotate(actions)
        A = np.concatenate([A, actions], axis=0)
    del states, actions # メモリ解放
    '''後略'''

これで，stateとactionの組が約4856万セットできました．
このままだとデータが対局の順番になっているので，シャッフルしたうえで訓練データとテストデータに分割し，保存します．

load.py

def main():
    with open("../policy_data/txt/data.txt", "r") as f:
    '''中略'''
    del states, actions

    print("Saving data...")
    data_size = A.shape[0]
    test_size = 1000
    rands = np.random.choice(data_size, data_size, replace=False)
    S_test = S[rands[:test_size],:,:] # 1000個はテスト用
    A_test = A[rands[:test_size]]
    np.save('../policy_data/npy/states_test.npy', S_test)
    np.save('../policy_data/npy/actions_test.npy', A_test)
    del S_test, A_test # メモリ解放
    S_train = S[rands[test_size:],:,:] # 残りは訓練用
    A_train = A[rands[test_size:]]
    np.save('../policy_data/npy/states.npy', S_train)
    np.save('../policy_data/npy/actions.npy', A_train)
    del S, A, S_train, A_train # メモリ解放

モデル構築

次はモデルの構築です．
AlphaGoのSLポリシーネットワークを元にして，図のようなモデルをChainerで書きました．
実際のAlphaGoは特徴抽出をして入力を48チャネルとしていますが，IaGoでは「黒石が存在するか」と「白石が存在するか」の2チャネルのみとしました．
その他は，層やチャネル数を減らすなどの小さな変更しか与えていません．

network.py

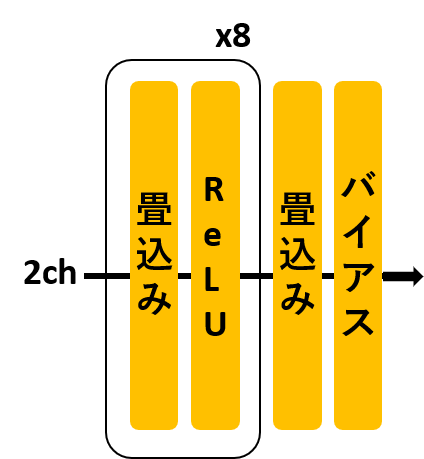
import chainer
import chainer.functions as F
import chainer.links as L

# 畳込みとReLUをブロックにまとめる
class Block(chainer.Chain):
    def __init__(self, out_channels, ksize, pad=1):
        super(Block, self).__init__()
        with self.init_scope():
            # 入力チャネル数をNoneとすると自動で設定される
            self.conv = L.Convolution2D(None, out_channels, ksize, pad=pad)

    def __call__(self, x):
        h = self.conv(x)
        return F.relu(h)

# SLポリシーネットワーク
class SLPolicy(chainer.Chain):

    def __init__(self):
        ksize = 3
        super(SLPolicy, self).__init__()
        with self.init_scope():
            self.block1 = Block(64, ksize)
            self.block2 = Block(128, ksize)
            self.block3 = Block(128, ksize)
            self.block4 = Block(128, ksize)
            self.block5 = Block(128, ksize)
            self.block6 = Block(128, ksize)
            self.block7 = Block(128, ksize)
            self.block8 = Block(128, ksize)
            self.conv9 = L.Convolution2D(128, 1, 1, nobias=True)
            self.bias10 = L.Bias(shape=(64))

    def __call__(self, x):
        h = self.block1(x)
        h = self.block2(h)
        h = self.block3(h)
        h = self.block4(h)
        h = self.block5(h)
        h = self.block6(h)
        h = self.block7(h)
        h = self.block8(h)
        h = self.conv9(h)
        h = F.reshape(h, (-1,64)) # -1にした要素は自動で設定される
        h = self.bias10(h)
        h = F.softmax(h, axis=1)
        return h

学習

図のように，盤面(state)を2チャネルに分けた入力から，64通りの打つ場所(action)に分類するモデルを学習させます．

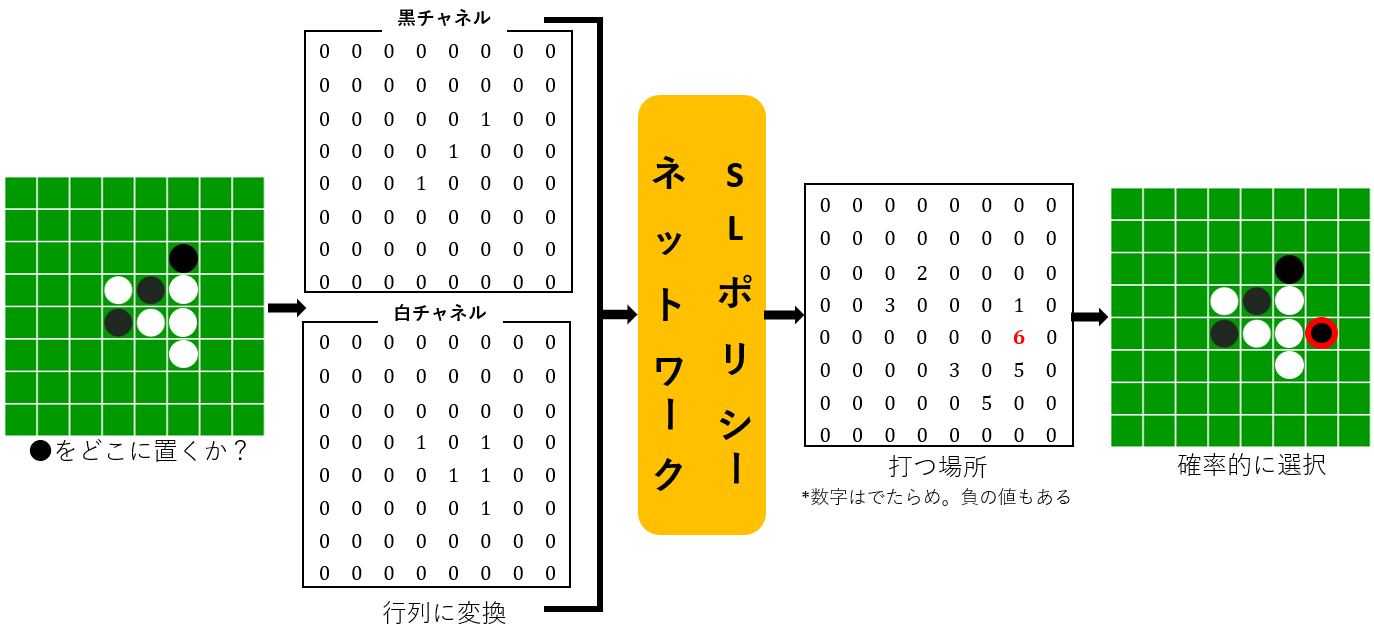
損失関数は交差エントロピー，最適化アルゴリズムはAdamとしました(AlphaGoではSGD)．

train_policy.py

import argparse
import numpy as np
from tqdm import tqdm
import chainer
import chainer.functions as F
import chainer.links as L
from chainer import serializers, cuda, optimizers, Variable
import network

# 教師データをGPU用に変換する
def transform(x, y):
    x = np.stack([x==1, x==2], axis=0).astype(np.float32)
    X = Variable(cuda.to_gpu(x.transpose(1,0,2,3)))
    Y = Variable(cuda.to_gpu(y.astype(np.int32)))
    return X, Y

def main():
    # エポック数とGPU番号の指定
    parser = argparse.ArgumentParser(description='IaGo:')
    parser.add_argument('--epoch', '-e', type=int, default=30, help='Number of sweeps over the dataset to train')
    parser.add_argument('--gpu', '-g', type=int, default="0", help='GPU ID')
    args = parser.parse_args()

    # モデル定義
    model = network.SLPolicy()
    optimizer = optimizers.Adam()
    optimizer.setup(model)
    optimizer.add_hook(chainer.optimizer_hooks.WeightDecay(5e-4))
    cuda.get_device(args.gpu).use()
    '''後略'''

次が学習部分です．
繰り返しになりますが，入力はstateそのものではなく，黒石が存在するかどうか，白石が存在するかどうかのbool配列を2チャネルで入力しています．
学習ループをtrainerで実装できればよかったのですが，わかりませんでした．
また，進捗状況を示すためにtqdmを利用しました．
1エポックの計算に1時間ほどかかります．

train_policy.py

def main():
    parser = argparse.ArgumentParser(description='IaGo:')
    '''中略'''
    cuda.get_device(args.gpu).use()

    X_test = np.load('../policy_data/npy/states_test.npy')
    y_test = np.load('../policy_data/npy/actions_test.npy')
    X_test, y_test = transform(X_test, y_test)
    X_train = np.load('../policy_data/npy/states.npy')
    y_train = np.load('../policy_data/npy/actions.npy')
    train_size = y_train.shape[0]
    minibatch_size = 4096 # 2**12

    # 学習ループ
    for epoch in tqdm(range(args.epoch)):
        model.to_gpu(args.gpu)
        # 訓練データのシャッフル
        rands = np.random.choice(train_size, train_size, replace=False)
        X_train = X_train[rands,:,:]
        y_train = y_train[rands]

        # ミニバッチ学習
        for idx in tqdm(range(0, train_size, minibatch_size)):
            x = X_train[idx:min(idx+minibatch_size, train_size), :, :]
            y = y_train[idx:min(idx+minibatch_size, train_size)]
            x, y = transform(x, y)
            pred_train = model(x)
            loss_train = F.softmax_cross_entropy(pred_train, y)
            model.cleargrads()
            loss_train.backward()
            optimizer.update()
        # ロスと正解率の計算
        with chainer.using_config('train', False):
            with chainer.using_config('enable_backprop', False):
                pred_test = model(X_test)
        loss_test = F.softmax_cross_entropy(pred_test, y_test).data
        test_acc = F.accuracy(pred_test, y_test).data
        print('\nepoch :', epoch, '  loss :', loss_test, ' accuracy:', test_acc)
        # ログ
        with open("../log/sl.txt", "a") as f:
            f.write(str(loss_test) + ", " + str(test_acc) + "\n")
        # モデル保存
        model.to_cpu()
        serializers.save_npz('../models/sl_model.npz', model)
        serializers.save_npz('../models/sl_optimizer.npz', optimizer)

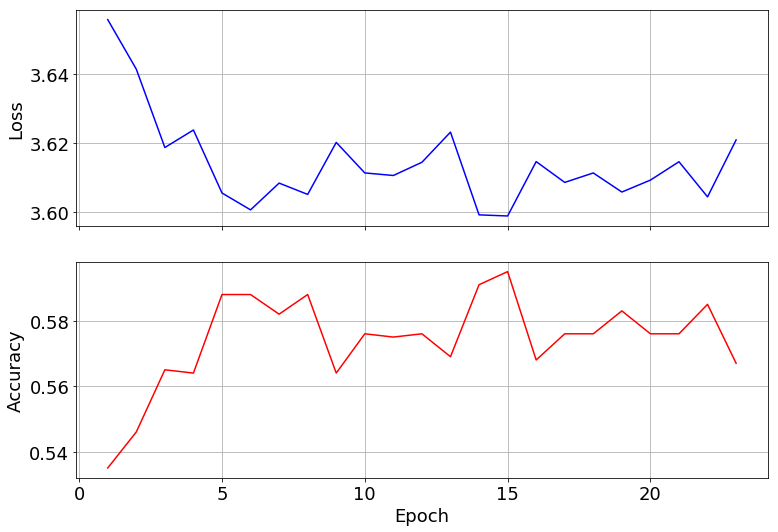
長めに学習させてロスと正解率を出力してみました．
5-15エポックくらいで十分そうですね．ちなみに，AlphaGoの正解率は57%程度だそうです．

ゲームの実装

ターミナル上で対話形式でプレイできるようにしました．
ルールを実装する部分が地味に大変でした．
詳細はソースコードのgame.pyとself_play.pyをご覧ください．

人間 vs AI

まずは，ゲームに必要な盤面などを定義します．
gamelogには棋譜を保存します．

game.py

class Game:

    def __init__(self):
        # 盤面の初期化
        self.state = np.zeros([8, 8], dtype=np.float32)
        self.state[4, 3] = 1
        self.state[3, 4] = 1
        self.state[3, 3] = 2
        self.state[4, 4] = 2
        # ゲーム内変数
        self.stone_num = 4 # 盤上の石の数
        self.play_num = 1 # 何手目か
        self.pass_flg = False # 前の手がパスならTrue
        self.date = datetime.now().strftime("%Y-%m-%d-%H-%M") # ログのファイル名に使う
        self.gamelog = "IaGo v1.3\n" + self.date + "\n"
        # モデル読込み
        self.model = L.Classifier(SLPolicy.SLPolicyNet(), lossfun=softmax_cross_entropy)
        serializers.load_npz('./models/sl_model.npz', self.model)

次に重要なのは，手を選択するインターフェイス部分です．
ここで，先ほど学習したSLポリシーネットワークが利用され，確率分布action_probabilitiesに従って手を選択します．
colorは石の色を表す変数で，１なら白番，２なら黒番を示します．

game.py

class Game:

    def get_position(self, color, positions):
        # 人間のターン(白番)
        if color==1:
            position = [int(e) for e in self.safeinput()]
            if not position in positions:
                print("This position is invalid. Choose another position")
                return self.get_position(color, positions) # ルール違反の場合はもう一度選ばせる
        # AIのターン(黒番)
        else:
            # SLポリシーネットワークで次の手を選択する
            X = np.stack([self.state==1, self.state==2], axis=0).astype(np.float32)
            state_var = chainer.Variable(X.reshape(2,1,8,8).transpose(1,0,2,3))
            action_probabilities = self.model1.predictor(state_var).data.reshape(64)
            action_probabilities -= np.min(action_probabilities) # 確率に変換するために，すべての要素を正にする
            distrib = action_probabilities/np.sum(action_probabilities)
            idx = np.random.choice(64, p=distrib) # 確率的に選択
            position = [idx//8+1, idx%8+1]
            if not position in positions:
                # ルール違反の場合はもう一度選ぶ
                return self.get_position(2, positions)
        return position

次に，石を置いて挟まれた石を裏返すplace_stoneや，盤面を表示するshow，合法手の選択肢を返すvalid_posなどの関数を定義してから，1ターンで行う処理をturn関数にまとめます．

game.py

class Game:

    def turn(self, color):
        players = ["You", "AI"]
        positions = self.valid_pos(color) # 合法手の座標
        print("Valid choice:", positions)
        if len(positions)>0:
            # 合法手が存在するなら，石を置く座標を選択する
            position = self.get_position(color, positions)
            self.place_stone(position, color)
            self.show()
            self.pass_flg = False
            self.gamelog += "[" + str(self.play_num) + "]" + players[color-1]\
             + ": " + str(position) + "\n"
            self.stone_num += 1
        else:
            # 合法手が存在しないならパス
            if self.pass_flg:
                self.stone_num = 64 # パスが２回続いたらゲーム終了
            print(players[color-1] + " pass.")
            self.pass_flg = True
            self.gamelog += "[" + str(self.play_num) + "]" + players[color-1] + ": Pass\n"
        self.play_num += 1

最後に，ゲームの開始から終了までの処理をmain関数にまとめます．

game.py

def main():
    print("\n"+"*"*34)
    print("*"*11+"Game Start!!"+"*"*11)
    print("*"*34+"\n")
    game = Game()
    game.show()

    while(game.stone_num<64): # 盤が埋まるまで繰り返す
        game.turn(1)
        game.turn(2)

    print("\n"+"*"*34)
    print("*"*12+"Game End!!"+"*"*12)
    print("*"*34)
    jd = game.judge()
    print(jd)
    game.gamelog += jd + "\n"
    game.save_gamelog()

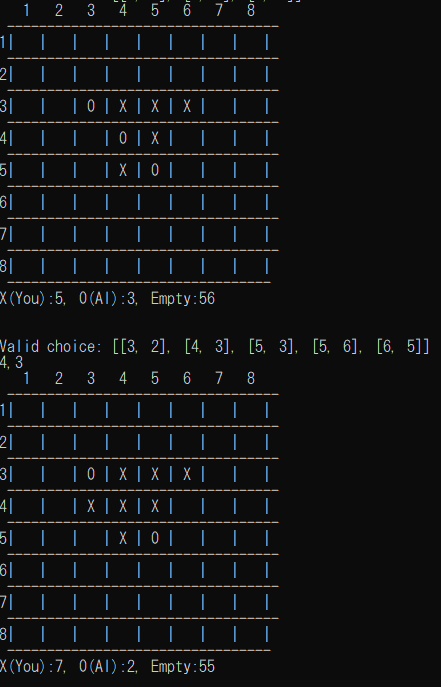
game.pyを実行すると，こんな感じで対戦が進みます．

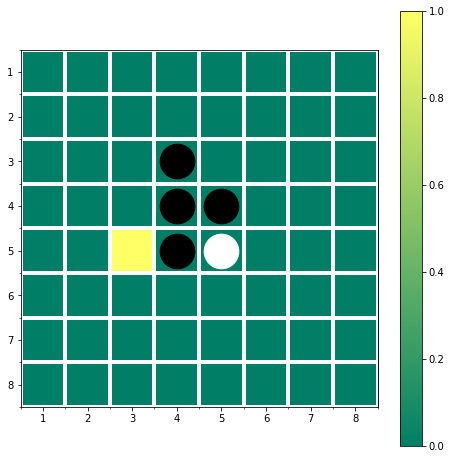
途中でaction_probabilitiesを取り出し，カラーマップで表示してみました．
AIが各マスに白石を置く確率が色で示されています．
[5,3]を除いて，他のマスはほぼ確率0になっています．[3,3]や[3,5]も悪手なのでしょうか．

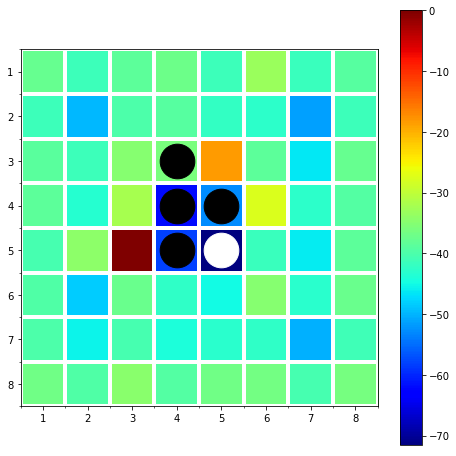
色を対数スケールにしてみると，小さい値の差がはっきりします．

おもしろい結果ですね！
[2,2]や[7,7]のような「四隅の1つ内側」は確率が非常に低くなっていて，悪手であることが学習されています．
また，同じ合法手でも[3,3]と[3,5]はかなり違いがあります．

AI vs AI

game.pyのget_position関数で，人間のターンのところもSLポリシーネットワークで手を選択させれば，AIの自己対戦ができます．
コードがうまく動くかのテストにも使えるので，実装しておくと便利です．

self_play.py

from game import Game

class SelfGame(Game):

    def get_position_self(self, color, positions):

        # AIが黒番のときは黒と白を入れ替えたものを入力する
        if color==1:
            tmp = 3*np.ones([8,8], dtype=np.float32)
            self.state = self.state*(tmp-self.state)*(tmp-self.state)/2

        # SLポリシーネットワークで次の手を選択する
        X = np.stack([self.state==1, self.state==2], axis=0).astype(np.float32)
        state_var = chainer.Variable(X.reshape(2,1,8,8).transpose(1,0,2,3))

        if color==1:
            action_probabilities = self.model1.predictor(state_var).data.reshape(64)
        else:
            action_probabilities = self.model2.predictor(state_var).data.reshape(64)

        action_probabilities -= np.min(action_probabilities) # 確率に変換するために，すべての要素を正にする
        distrib = action_probabilities/np.sum(action_probabilities)
        idx = np.random.choice(64, p=distrib) # 確率的に選択
        position = [idx//8+1, idx%8+1]
        if not position in positions:
            # ルール違反の場合はもう一度選ぶ
            return self.get_position_self(color, positions)
        return position

最後までお読みいただきありがとうございました！
次回記事はこちら．
AlphaGoを模したオセロAIを作る(2): RLポリシーネットワーク - Qiita

参考文献

[1] D. Silver et al., "Mastering the game of Go with deep neural networks and tree search," nature, Vol. 529, No. 7587, pp. 484-489, 2016.
DeepMindによるAlphaGoの論文です．

[2] 大槻知史, 三宅陽一郎, 『最強囲碁AI アルファ碁 解体新書 深層学習，モンテカルロ木探索，強化学習から見たその仕組み』, 翔泳社, 2017.
原著論文[1]の解説書です．非常にわかりやすかったです．

[3] 720万手をディープラーニングで学習したオセロＡＩをChainerで作ってみた - Qiita
モデルの構築やルールの実装などで参考にさせていただきました．

[4] AlphaGoの論文解説とAIが人間を超えるまで - A Successful Failure
無料で読めるものだとこれがわかりやすいです．