はじめに
本記事は全4回連載の最終回です.ここまで長い道のりでした…!
前回の記事はこちら.
AlphaGoを模したオセロAIを作る(3): バリューネットワーク - Qiita
また,ソースコードの全文はこちらにあります.
これまでに作ったSLポリシーネットワークとバリューネットワークを使って,**モンテカルロ木探索(Monte Carlo tree search; MCTS)**というアルゴリズムでゲーム木を賢く探索することで先読みを行います.
ロールアウトポリシー
まず,SLポリシーネットワークを単純化したロールアウトポリシーを作ります.
モンテカルロ木探索では,ゲーム木の葉ノード(局面)からあるポリシーに従って終局までシミュレーションを実行すること(プレイアウトと呼びます)を何度も繰り返し,その結果をノードの評価値に利用します.
プレイアウト回数が多ければ多いほど評価の精度が高くなりますが,推論にかかる計算時間が長いと少ししかプレイアウトができません.
そこで,SLポリシーネットワークより精度は落ちるものの高速に動作するようなロールアウトポリシーを代わりに使うことにします.
ロールアウトポリシーは畳込み1層とソフトマックス出力層で構成しました.このため「ネットワーク」とは呼びません.
class RolloutPolicy(chainer.Chain):
def __init__(self):
super(RolloutPolicy, self).__init__()
with self.init_scope():
self.conv1 = L.Convolution2D(None, 1, 3, nobias=True, pad=1)
self.bias2 = L.Bias(shape=(64))
def __call__(self, x):
h = self.conv1(x)
h = F.reshape(h, (-1,64))
h = self.bias2(h)
h = F.softmax(h, axis=1)
return h
これをSLポリシーネットワークと同様にtrain_policy.pyで訓練します.1エポックで十分です.
ここで,ロールアウトポリシーとSLポリシーネットワークの性能を比較してみましょう.
| モデル | 正解率 | 計算時間 | 学習エポック数 |
|---|---|---|---|
| SLポリシー | 59.5% | 0.007 sec | 15 |
| ロールアウト | 25.5% | 0.002 sec | 1 |
モンテカルロ木探索
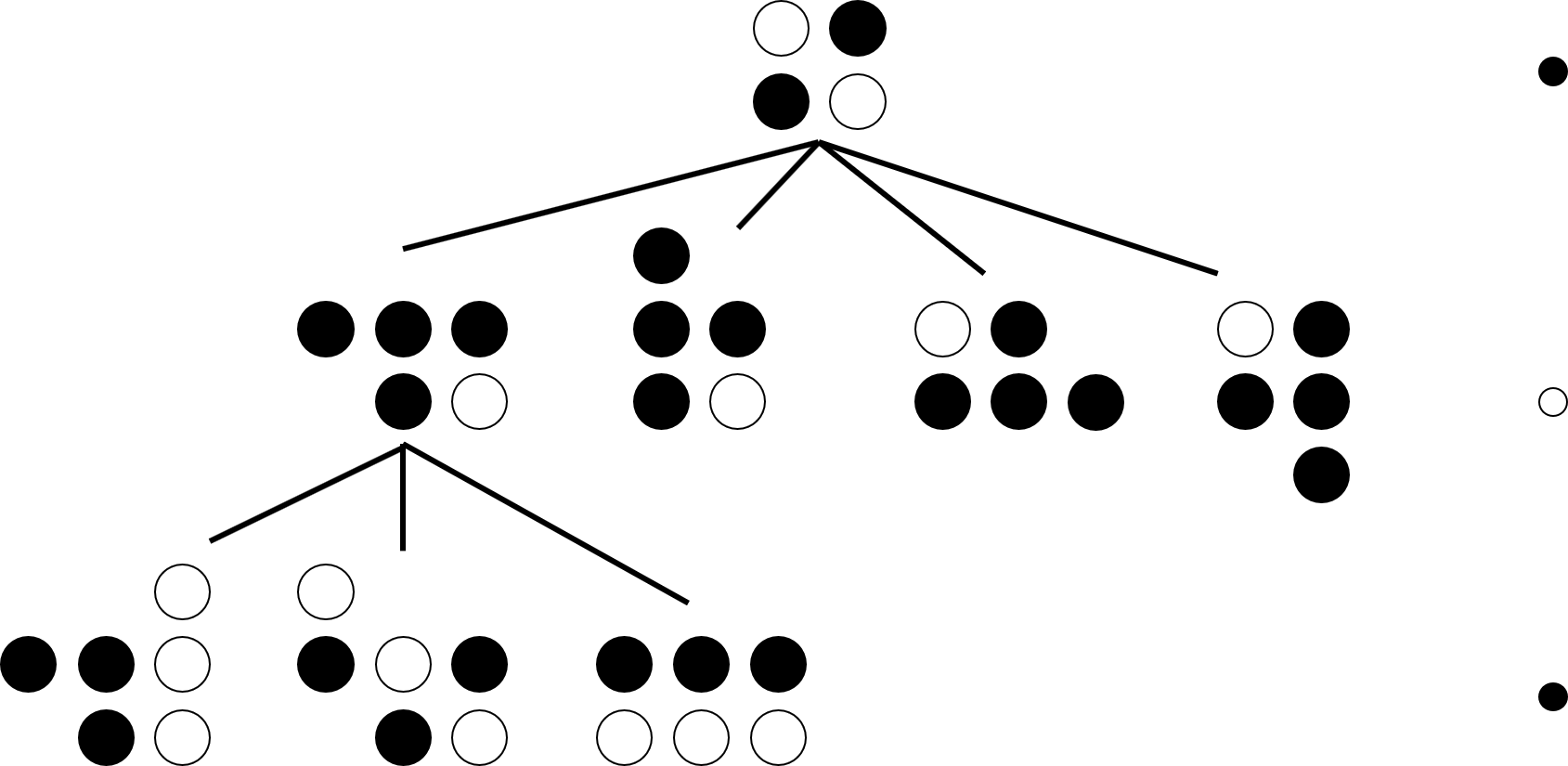
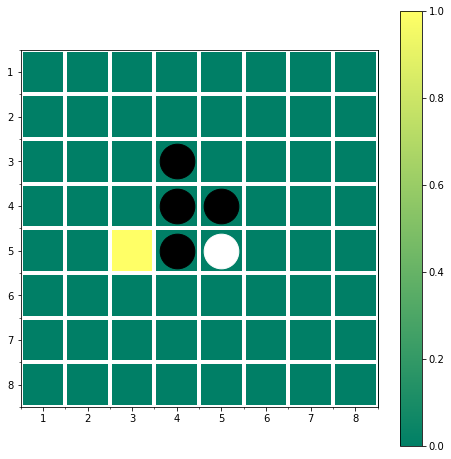
簡単なゲーム木の図を描いてみました.
オセロの探索木の主な特徴は,子ノードの数が不定であることと,深さによって打つプレイヤーが変わることでしょうか.
子ノードの数は合法手の数です.探索空間の広さは(子ノードの数)^(深さ)で大きくなっていくので,単純な幅優先探索や深さ優先探索では現実的な時間で最良の手を探せません.
そこで,勝ちにつながる見込みの高い手だけを集中的に探索しようというのが,モンテカルロ木探索の近似的アプローチ(ヒューリスティクス)です.
従来のモンテカルロ木探索では「勝ちにつながるかどうか」をランダムなプレイアウトの結果によって評価していましたが,AlphaGoではロールアウトポリシーによるプレイアウトとバリューネットワークの組合せによって行います.
これにより高い精度での先読みが可能になりました.
木の実装ですが,まずはNodeクラスおよび必要なプロパティとメソッドを定義しましょう.
import numpy as np
import copy
import chainer
from chainer import serializers, cuda, optimizers, Variable
import network
import mcts_self_play
from game import GameFunctions as gf
class Node(object):
def __init__(self, parent=None, prob=0):
self.parent = parent # 親ノード
self.children = {} # 子ノードのディクショナリ
self.n_visits = 0 # ノードの訪問回数
self.Q = 0 # 評価値計算に使う
self.u = prob+0.1 # 評価値計算に使う
self.P = prob+0.1 # 評価値計算に使う
# 親ノードか?
def is_root(self):
return self.parent is None
# 葉ノードか?
def is_leaf(self):
return len(self.children)<1
# 評価値計算
def get_value(self):
return self.Q + self.u
インポートしたmcts_self_playのクラスSimulateは,盤面と色を引数にとり,そこからロールアウトポリシーによるプレイアウトの結果を返すクラスです.
さて,AlphaGoのモンテカルロ木探索は,次の4ステップからなります.
- 選択ステップ
- 展開ステップ
- 評価ステップ
- 更新ステップ
それぞれについて詳しく見ていきましょう.
選択ステップ
最も評価値の高い子ノードを選びながら葉ノードまで木を降りていきます.
評価値は次で定義される$Q(s,a)$と$u(s,a)$の和です.
\begin{eqnarray}
Q(s,a) &=& (1-\lambda)\frac{V(s,a)}{N(s,a)} + \lambda\frac{Z(s,a)}{N(s,a)}\\
u(s,a) &=& C_{puct}\,P(s,a)\frac{\sqrt{\sum_b N(s,b)}}{0.01+N(s,a)}
\end{eqnarray}
$s$と$a$は今の盤面と次の手の組で,ノードを表します.
$V(s,a)$は$a$を選択した後のバリューネットワークの出力の合計,$Z(s,a)$はプレイアウトの勝敗の合計, $N(s,a)$はそのノードの訪問回数です.
$\lambda=0.5$はバリューネットワークの出力とプレイアウトの勝敗に重みを付けるパラメータです.
これらを訪問回数$N(s,a)$で平均することによって,$Q(s,a)$は2つの観点から「勝てる見込み」を算出します.
次に$u(s,a)$についてです.
$P(s,a)$はSLポリシーネットワークから得られる選択確率,$\sum_b N(s,b)$は当該ノードと兄弟ノードの訪問回数の和です.
これは,選択確率に,訪問回数が少ないと大きくなるような項をかけて補正をしていることになります.
$C_{puct}=1$は$Q(s,a)$と$u(s,a)$に重みを付けるパラメータです.
少し話がそれてしまいましたが,「最も評価値の高い子ノードを選ぶ」関数は次のように実装できます.
返り値は手と次のノード(選んだ子ノード)のタプルです.
class Node(object):
```中略```
def select(self):
# 兄弟ノードの値を更新
for k in self.children:
self.children[k].u = self.children[k].U(c_puct)
return max(self.children.items(), key=lambda act_node: act_node[1].get_value())
def U(self, c_puct):
return c_puct * self.P * np.sqrt(self.parent.n_visits) / (0.01 + self.n_visits)
展開ステップ
葉ノードに達したときに,SLポリシーネットワークの出力から得られる合法手と確率の組のリストから,各組を子ノードとしてゲーム木に追加していきます.
展開ステップに進むのは,「当該葉ノードの訪問回数が閾値(15)を超えたら」という条件がついていますが,この制御は後で行います.
class Node(object):
```中略```
def expand(self, action_probs):
for action, prob in action_probs:
if action not in self.children:
self.children[action] = Node(self, prob)
評価ステップ
当該葉ノードで訪問回数が閾値(15)を超えない場合,ロールアウトポリシーでプレイアウトを実行し,勝敗を$z$に保存します.
z = \left\{ \begin{array}{ll}
1 & (Win) \\
0 & (Draw) \\
-1 & (Lose)
\end{array} \right.
また,バリューネットワークの出力を$v$に保存します.
この操作が何度か行われることで,ノードの評価値の精度が向上します.
実装は後述のplayout関数とevaluate_rollout関数を見てください.
更新ステップ
評価ステップで得られた$z$と$v$ノードの評価値を更新します.
当該ノードの更新が終わったら,ゲーム木を1つずつ遡りながら,ルートノードに至るまで同じ$v$と$z$の値で評価値を更新します.
このとき,兄弟ノードの評価値($u(s,a)$)は更新せず,選択ステップで行っています.
更新を行う関数では,評価ステップで得られた葉ノードの結果($(1-\lambda)v+\lambda z)$)を引数とします.
class Node(object):
```中略```
def update(self, leaf_value, c_puct):
# 訪問回数
self.n_visits += 1
# 漸化式(後述)
self.Q += (leaf_value - self.Q) / self.n_visits
def update_recursive(self, leaf_value, c_puct):
self.update(leaf_value, c_puct)
# ルートノードに至るまで1手ずつ遡る
if not self.is_root():
self.parent.update_recursive(leaf_value, c_puct)
更新で利用した漸化式の導出を示しておきます.
\begin{eqnarray}
\Delta Q(s,a) &=& Q_{N+1}(s,a)-Q_{N}(s,a)\\
&=& (1-\lambda)\frac{V(s,a)+v}{N(s,a)+1} + \lambda\frac{Z(s,a)+z}{N(s,a)+1} - \biggl( (1-\lambda)\frac{V(s,a)}{N(s,a)} + \lambda\frac{Z(s,a)}{N(s,a)}\biggr)\\
&=& \frac{(1-\lambda)v+\lambda z +N(s,a)Q(s,a)-(N(s,a)+1)Q(s,a)}{N(s,a)+1}\\
&=& \frac{(1-\lambda)v+\lambda z-Q_{N}(s,a)}{N(s,a)+1}
\end{eqnarray}
全体の制御
今作ったNodeクラスを利用して,モンテカルロ木探索全体にかかわる部分を作っていきます.
class MCTS(object):
def __init__(self, lmbda=0.5, c_puct=1, n_thr=15, time_limit=10):
self.root = Node(None, 1.0) # ルートノード
self.policy_net = network.SLPolicy()
serializers.load_npz('./models/sl_model.npz', self.policy_net)
self.value_net = network.Value()
serializers.load_npz('./models/value_model.npz', self.value_net)
# 推論時の高速化のための設定
chainer.config.train = False
chainer.config.enable_backprop = False
self.lmbda = lmbda
self.c_puct = c_puct
self.n_thr = n_thr # 訪問回数の閾値
self.time_limit = time_limit # 持ち時間
# 合法手と出力確率の組の配列を返す
def policy_func(self, state, color, actions):
state_var = gf.make_state_var(state, color)
prob = self.policy_net(state_var).data.reshape(64)
action_probs = []
for action in actions:
action_probs.append((action, prob[action]))
return action_probs
# バリューネットワークの出力を返す
def value_func(self, state, color):
state_var = gf.make_state_var(state, color)
return self.value_net(state_var).data.reshape(1)[0]
メインとなるのは次のplayout関数です.
class MCTS(object):
```中略```
def playout(self, state, color, node):
node = node.copy()
c = color
if node.is_leaf():
# 葉ノードに達したら
if node.n_visits >= self.n_thr:
# 訪問回数が閾値を超えていれば拡張ステップへ
actions = gf.legal_actions(state, c)
if len(actions)<1:
# パス
node.children[-1] = Node(node, 1)
if len(actions)==1:
# 選択肢が1つ
node.children[actions[0]] = Node(node, 1)
else:
action_probs = self.policy_func(state, c, actions) # 合法手と選択確率の組の配列
node.expand(action_probs)
self.playout(state, c, node)
else:
# 閾値を超えていなければ評価ステップへ
v = self.value_func(state, color) if self.lmbda < 1 else 0
z = self.evaluate_rollout(state, color) if self.lmbda > 0 else 0 # プレイアウト実行
leaf_value = (1-self.lmbda)*v + self.lmbda*z
# 更新ステップ
node.update_recursive(leaf_value, self.c_puct)
else:
# 葉ノードに至るまでは選択ステップ
action, node = node.select(self.c_puct)
state = gf.place_stone(state, action, c)
c = 3-c
self.playout(state, c, node) # 再帰
# ロールアウトポリシーによるプレイアウトを実行し結果を返す
def evaluate_rollout(self, state, color):
sim = mcts_self_play.Simulate(state)
return sim(color)
playout関数は持ち時間が尽きるまで繰り返し実行されます.
時間を管理し,gameクラスと入出力をやり取りをするのがget_move関数です.
なお,最後に出力するのは「最も評価値の高い手」ではなく「最も訪問回数の多い手」です.
訪問回数が十分大きければ両者は一致しますが,少ないときは後者の方が真の値に近いからです.
class MCTS(object):
```中略```
def get_move(self, state, color):
start = time.time()
elapsed = 0
while elapsed < self.time_limit:
# 持ち時間が尽きるまでプレイアウトを繰り返す
state_copy = state.copy()
self.playout(state_copy, color, self.root)
elapsed = time.time()-start
return max(self.root.children.items(), key=lambda act_node: act_node[1].n_visits)[0]
石を置いて盤面が変化したらルートノードを更新します(これはどちらの手番でも必要です).
選ばれた手が子ノードの中に含まれればそれを新たなルートノードとし,含まれなければ新しく作ります.
class MCTS(object):
```中略```
def update_with_move(self, last_move):
if last_move in self.root.children:
self.root = self.root.children[last_move]
self.root.parent = None
else:
self.root = Node(None, 1.0)
パラメータ調節について
以上でIaGoの完成です!
最後に,パラメータ調節に少し苦労したので補足させてください.
第1回で見たように,IaGoのSLポリシーネットワークはほぼ決定的になっています.
このままでは盤面の評価値はほとんどこれで決まるため,1つの手だけを探索してしまい,ゲーム木に広がりが生まれません.
そのため,IaGoではAlphaGoから意図的に2点の変更を加えました.
1つめは,全ノードの選択確率にベースラインとして0.1を加えたことです.
2つめは,$u(s,a)$の補正項の分母の1を0.01とし,補正の効果を強めたことです.
これらの変更により,訪問回数の少ないノードが選ばれやすくなりました.
おわりに
微妙なパラメータの違いでパフォーマンスが大きく変わるので,今のパラメータが最適とは言えませんが,平均的な人のレベルには達したように感じます.
また,強さの客観的な評価はできていませんが,少なくとも単純なSLポリシーネットワークよりは強いです.
ただ,実際に対戦してみると,相手に四隅を譲るような悪手がたまに出てしまいます.
目下の課題は強化学習をやり直すことと,シミュレーションを高速化してプレイアウト回数を増やすことです.
そして,時間に余裕があったらwebアプリケーションやスマホアプリにしたいと思っています.
他にもお気づきの点がございましたらぜひコメントください.
最後までお読みいただきありがとうございました!
P.S.
IaGoと対戦していくうちに,自分のオセロのレベルがぐんと上がったことを実感しました.
親が子から学ぶとはまさにこのことですね.
参考文献
[1] D. Silver et al., "Mastering the game of Go with deep neural networks and tree search," nature, Vol. 529, No. 7587, pp. 484-489, 2016.
DeepMindによるAlphaGoの論文です.
[2] 大槻知史, 三宅陽一郎, 『最強囲碁AI アルファ碁 解体新書 深層学習,モンテカルロ木探索,強化学習から見たその仕組み』, 翔泳社, 2017.
原著論文[1]の解説書です.非常にわかりやすかったです.
[3] Rochester-NRT/RocAlphaGo
有志によるAlphaGo再現プロジェクトです.コードを参考にしました.