IOTが流行してから、機械を予知保全すべく、センサをどんどん増やす取り組みが
行われています。
噂では、1台の機械にセンサ100個を付ける事例も出てきたようです。
そこで疑問に思うのは、センサの個数を増やすことは正義なのか?
言い換えると、余分なセンサを増やしても異常検知性能に影響がないのか?と
いうことです。
本稿では、次元の呪いに焦点を当て、「余分なセンサの個数を増やした場合、異常検知
性能がどうなるのか」を検証します。
※コード全体はこちらに置きました。
※こちらはPythonデータ分析勉強会#17の発表資料です。
結論から
- 余分なセンサ情報があると、異常検知性能が下がる可能性がある
- それを避けるには、余分なセンサを削減するなどの工夫が必要
想定するシーン
- 異常検知で有効なセンサは2つだけ
- 余分なセンサも付いておりほぼゼロ信号を出しているが、ノイズが含まれる(重要)
- 余分なセンサを増やしていった場合、異常スコアがどうなるのか?
結論からいってしまうと、余分なセンサがゼロ信号を出し続ければ、異常検知性能は
ほとんど変わらないと言えます。ところが、ノイズが含まれるがために次元の呪いに
の影響を受け、センサ数を増やしていくと、異常検知性能が悪化します。
ノイズ
センサには必ずといっていいほど、ノイズが含まれます。精度が良いセンサでも
微小なノイズが含まれます。ノイズを除去するために、ロー(ハイ)パスフィルター
などを設置する対策もありますが、そういった処理は本稿の対象外とします。
本稿では、ノイズを含んだセンサの生データを使うシーンを想定します。
次元の呪いとは
データの次元数を増やしていくと、表面の体積が全体に体積のほとんどを占める
ようになる現象です。機械学習で問題となるのは、最近傍点と最遠方点の距離の差が
ほぼなくなり、距離による判別が難しくなる点です。詳しくは以下の記事をご覧ください。
教師あり学習への影響
個人的には、教師あり学習では**次元削減などを明示的に組み込めるため、次元の呪いの
影響を受けにくいと考えています。**極端な話し、余分なセンサ情報があったとしても
不要な特徴量をどんどん削減して、精度が一番出る特徴量を使えば良いともいえます。
教師なし学習への影響
ところが、異常検知などの教師無し学習では、基本的に異常データが無い、もしくは
少量の異常データしか手元にないシーンが考えられます。そして、少量の異常データを
参考に特徴量を削減すると、本当に必要な特徴量を削減してしまう危険性があります。
そのため、教師無し学習で安易に次元を削減すると、異常検知性能が劣化してしまう可能性が
あります。
かといって、不要なセンサ情報をそのまま検知器に入れて良いのか?異常検知性能が
劣化するのではないか?という疑問もわいてきます。つまり、不要なセンサ情報を
入れたがゆえに次元数が上がり、次元の呪いによって正常/異常の区別が付きにくく
なるのではないか?という疑問です。そこで、ダミーデータを使って実験を行います。
実験
- 異常検知で有効なセンサは2つだけ
- 余分なセンサも付いておりほぼゼロ信号を出しているが、ノイズが含まれる
- 余分なセンサを増やしていった場合、異常スコアがどうなるのか?を観察する
冒頭でも述べたように、上記の設定で実験を行います。
異常検知手法として以下の二つを使います。
- MT法
- Isolation Forest
細かい紹介は割愛しますが、MT法は正常データを正規分布に当てはめマハラノビス距離で
異常かどうか判別します。マハラノビス距離が大きいほど、異常度が高いです。
Isolation Forestは決定木ベースの異常検知手法です。本家の論文では500次元を
超えるデータに対しても有効であることが示されています。
コード全体はこちらに置きました。
MT法の結果
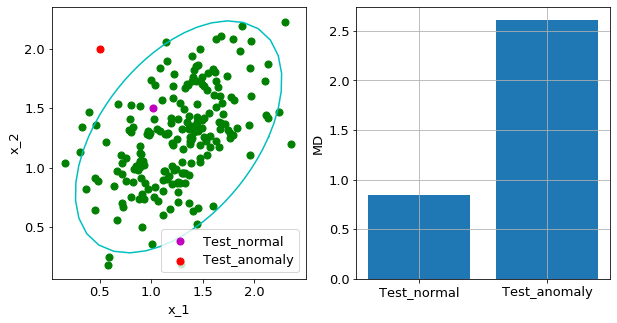
まずは、効いているセンサ($x_1,x_2$)を乱数を使って生成します。
上の左図より、$x_1,x_2$に相関があることが分かります。
緑の点が学習データです。$x_1$を温度、$x_2$を圧力などと置き換えると
分かりやすいかもしれません。
そして、紫の点が正常データ、赤の点が異常データです。
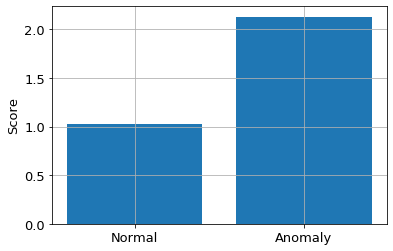
$x_1,x_2$空間でMT法を適用した場合、上の右図のように正常/異常で
はっきりと異常スコア(MD=マハラノビス距離)に違いが表れます。
マハラノビス距離が大きいほど、異常度が高いです。ちなみに、水色の線は
等確率楕円といって、マハラノビス距離が同じ領域を線で表しています。
次元数を2→3にした場合
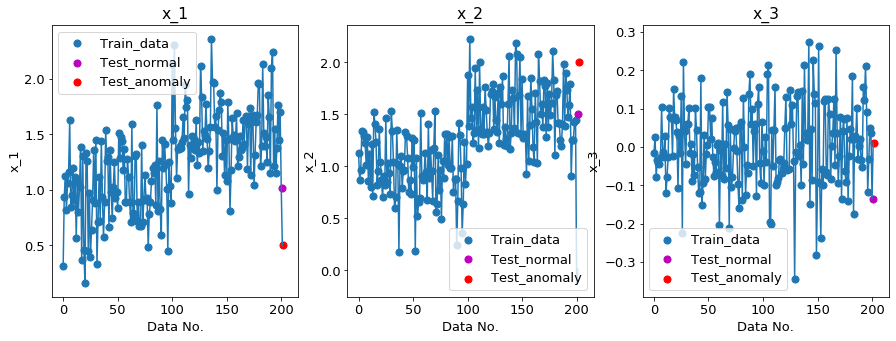
次元数を1個($x_3$)増やします。
上の右図($x_3$)のような、余分なセンサ情報を一つ追加しました。$x_3$は例えば、明度のセンサを
付けたとしても良いです。$x_1,x_2$(左と真ん中の図)は相関があり意味のあるデータでしたが、
$x_3$は相関もなく、ただノイズがのっているだけのデータになっています。
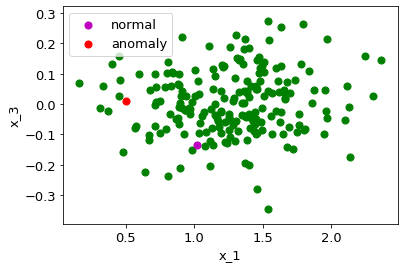
$x_1,x_3$空間を図示すると以下になります。
この図だけを見ると、正常/異常データの差はあまり大きくなく、ノイズの乗り方に
よっては、正常データの方が外れ値になることもありそうです。そして、それこそが
異常/正常の判別を難しくさせる要因です。
$x_1,x_2,x_3$空間全体でMT法を適用すると異常スコアは以下になります。
次元数が2の場合よりも、差が縮まりましたが、まだ異常データの方がスコアが
大きくなっています。
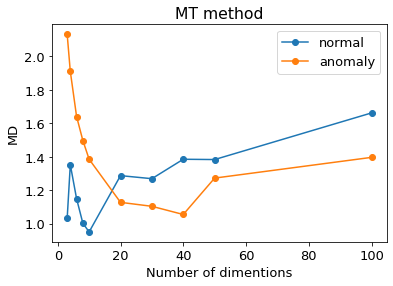
次元数を3→100にした場合
さきほどのような$x_3$を98個まで増やし続けた結果は以下のとおりです。
横軸は次元数、縦軸は異常スコア(MD=マハラノビス距離)です。
ご覧のとおり、次元数が20のところで、正常と異常のスコアが反転してしまいました。
つまり、誤検知しています。
乱数を使った実験なので、実験毎に結果が変わりますが、どの結果も次元数が小さいうちは
正常と異常が正しく検知できました。
Isolation Forestの結果
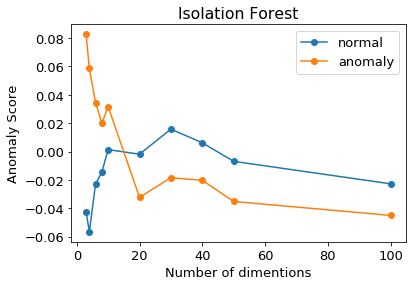
次元数を2→100にした場合
MT法と同じような結果になりました。
やはり、次元数が20のところで正常と異常が反転し、誤検知しています。
なお、Isolation Forestはscikit-learnを用いていますが、異常スコアは分かりやすさのために
数字を反転させています。(上の図では、異常スコアは大きいほど、異常度が高い。)
次元の呪いを避けるには
結果的に、不要なセンサ情報を入れすぎると、次元数が上がり、次元の呪いによって
正常/異常の判別が難しくなってしまいました。かといって、むやみにセンサ情報を
落とすと、異常検知性能が劣化してしまう危険性もあります。このジレンマを解決する
方法として以下が挙げられます。
-
コサイン類似度
一般的に、コサイン類似度など角度ベース手法は次元の呪いの影響を受けにくいと(←どこかで見た気がするのですが、出典元が思い出せず、今のところ
言われています。
消しています。どなたか参考文献や記事など、ご存知でしたら教えてください。) -
センサ情報を小分けにする
例えば、100個のセンサ情報があったとして、これらを一つの検知器に突っ込むのではなく
ここではセンサ情報を2個ずつに分けて検知器を作るアイデアです。これにより、次元の呪いの
影響を緩和できます。総当たりで検知器を作ったとして、$100C_2=4950$個の検知器を作ることに
なります。4950個の検知器の処理速度が気になりますが、MT法であれば高速に処理できます。
Isolation Forestは処理が重いため、リアルタイムの処理は難しいですが、オフラインであれば
使えるレベルだと思います。ただし、2個の関係性しか見ていないため、3個以上の関係性が
ある場合、異常を見逃してしまう可能性もあります。 -
余分なセンサを削減する
これが一番、簡単明瞭です。**異常データが手元にあれば、どのセンサ情報が効いているのか
絞ることができます。**これにより、余分なセンサを削除し、高次元化をさけることが
できます。ただし、冒頭でも述べたように、異常データが少量だと本当に必要なセンサを
削減してしまう危険性があること、異常データが無い場合、異常データを収集しながら
検知器をバージョンアップする必要があること、などが欠点です。MT法はSN比を使うことで
効いているセンサを絞ることができます。次回の記事では、MT法に限らず他の手法であっても
効いているセンサを絞る方法を紹介します。
まとめ
- 余分なセンサ情報を増やし続けると、異常検知性能が下がる可能性がある
- それを避けるには、~~コサイン類似度を使う、~~センサ情報を小分けにする、などの工夫が必要
- 余分なセンサを削減できれば、異常検知性能の劣化も避けられるしコスト削減になるし、一石二鳥
次回は、異常検知原因を探る手法を紹介します。
この手法を使えば、効いているセンサを絞ることができ、余分なセンサを削減することが可能です。