今回は第3回目です。
Pythonデータ分析勉強会 第1回資料
Pythonデータ分析勉強会 第2回資料
Pythonデータ分析勉強会 第3回資料
第1回、第2回の資料を見れば、Pythonを使ってデータ分析が進められると思います。
今回は、MT法の説明がメインです。機械学習に興味がある方は、本稿を飛ばして「scikit-learn」を、
ディープラーニングに興味がある方は「Keras」を勉強すると、理解が進むと思います。
※ 塩尻市内でPythonデータ分析勉強会を開催します。初心者の方も是非参加してください!
第2回 演習の答え
その1
import numpy as np
import matplotlib.pyplot as plt
A = np.sin(2*np.pi*np.array(range(100))/100)
plus, minus = [], []
for i in A:
if i > 0:
plus.append(i)
else:
minus.append(i)
np.savetxt("All.csv", A, delimiter=",")
np.savetxt("plus.csv", plus, delimiter=",")
np.savetxt("minus.csv", minus, delimiter=",")
plt.figure()
plt.title("All")
plt.plot(A)
plt.show()
plt.figure()
plt.title("Plus")
plt.plot(plus)
plt.show()
plt.figure()
plt.title("Minus")
plt.plot(minus, c="red")
plt.show()
その2
import numpy as np
import matplotlib.pyplot as plt
def plot_csv(name):
x = np.loadtxt(name + ".csv", delimiter=",")
plt.figure()
plt.title(name)
plt.plot(x)
plt.show()
plot_csv("All")
plot_csv("Plus")
plot_csv("Minus")
MT法
概要
MT法は、一言でいうと「変数間の相関を考慮した距離を出し、その距離を見て異常かどうか判定する」
手法といえます。図にすると以下のようになります。
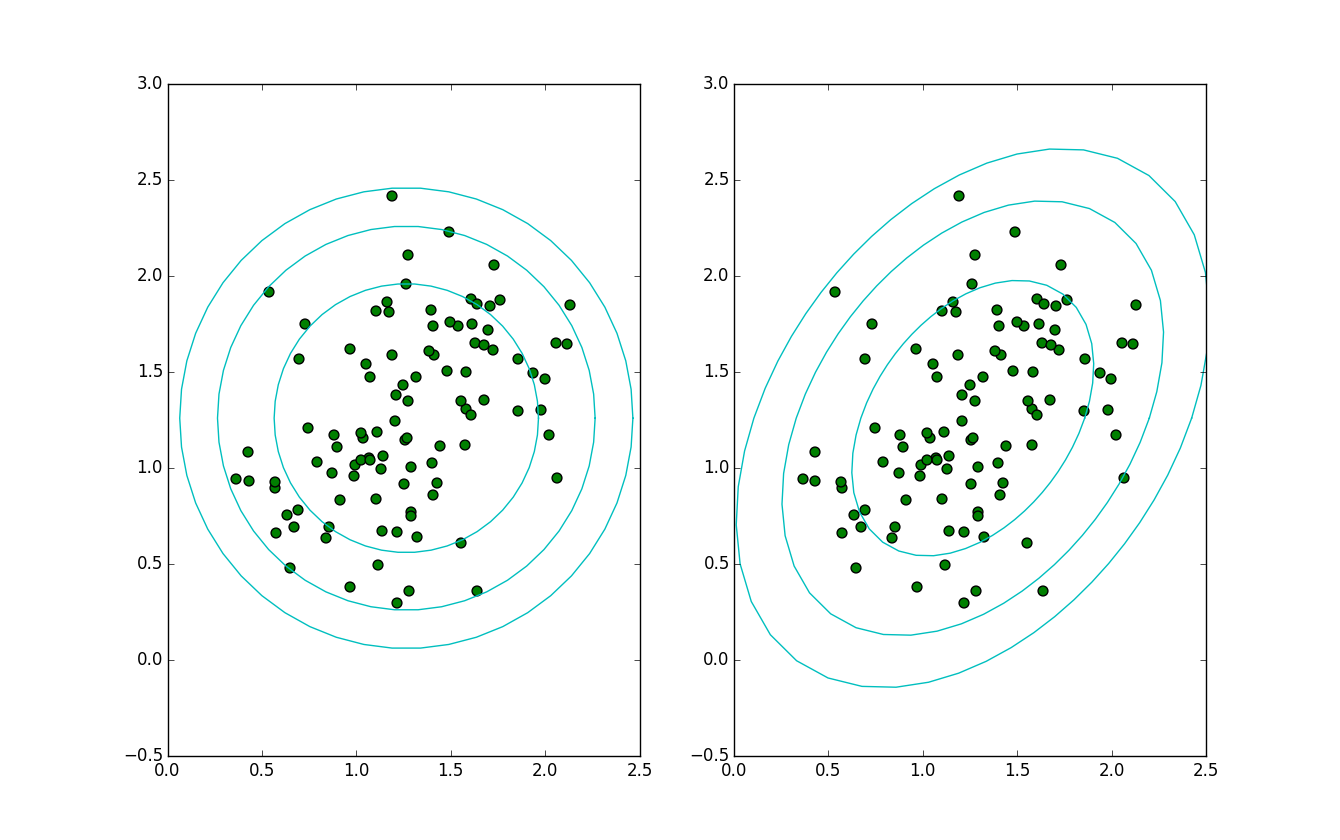
正常データの平均値を出して、平均値からの距離で異常検知することを考えます。
通常の距離(ユークリッド距離)を使うと左図にあるように、同心円状に広がっていきます。
ところが、変数間の相関を考慮した距離(マハラノビス距離)を使うと、右図のように楕円上に
広がる距離となります。
MT法では、マハラノビス距離が大きければ「異常」、小さければ「正常」と判定します。
理論
MT法の理論は、線形代数の知識が必要になります。ただ、理論を理解しなくても使うことはできるので、
お急ぎの方は、コード全文をご覧ください。MT法の数式は以下の資料が参考になります。
・http://kaz7227.art.coocan.jp/mt-system.pdf
・入門MTシステム
MT法は以下の流れで行っています。
まずは、左図にあるように正常データで平均値、標準偏差、相関行列を求め、単位空間を作成します。
そして、テストデータでマハラノビス距離を求め、その距離で異常かどうか判断します。
ここで、テストデータXが以下のように与えられたとします。
X=[X_{1},X_{2},・・・,X_{n}]
Xを使って、以下のようにマハラノビス距離が求められます。
\tilde{X} = [\frac{X_{1}-\bar{X_{1}}}{\sigma_{1}},\frac{X_{2}-\bar{X_{2}}}{\sigma_{2}},・・・,\frac{X_{n}-\bar{X_{n}}}{\sigma_{n}}]\\
D^2 = \frac{1}{n}\tilde{X}R^{-1}\tilde{X}^{T}
ただし、$\bar{X}$は各状態量の平均値、$\sigma$は各状態量の標準偏差、$R$は相関行列、$D$はマハラノビス距離です。
例題
ここでは、以下のデータが与えられたとして単位空間を作ってみます。
| X | Y | |
|---|---|---|
| データ1 | 10 | 20 |
| データ2 | 11 | 18 |
| データ3 | 9.5 | 22 |
XとYは状態量です。例えば、Xは機械の温度、Yは機械にかかる力と見なしても良いでしょう。
平均値を求める
最初に各状態量の平均値を求め、その平均値で引くという作業が必要になります。
表にすると、以下のとおりです。
・平均値を求める
| X | Y | |
|---|---|---|
| データ1 | 10 | 20 |
| データ2 | 11 | 18 |
| データ3 | 9.5 | 22 |
| 平均値(avg) | 10.2 | 20 |
・平均値で引く
| XX | YY | |
|---|---|---|
| データ1 | 10-10.2=-0.2 | 20-20=0 |
| データ2 | 11-10.2=0.8 | 18-20=-2 |
| データ3 | 9.5-10.2=-0.7 | 22-20=2 |
| 上の表で、新たな変数XX、YYを作っています。 |
コードにすると以下のとおりです。
import numpy as np
xx = np.copy(x)
avg = np.zeros(2)
# 各状態量から平均値を引く
for i in range(2):
avg[i] = np.mean(x[:,i])
for j in range(3):
xx[j,i] = x[j,i] - avg[i]
・xというのは、データが入ったnp配列(3行、2列)です。
・3行目でxをコピーしています。
・4行目で平均値配列(avg)の形を宣言しています。
・7行目以降はfor文です。rangeに2を与えているのは、xの列の数が「2」だからです。
・8行目で各列(状態量)毎に平均値を求めています。
・9行目以降もfor文になっています。7行目で、rangeに3を与えているのは、xの行数が「3」だからです。
・最後の行で、xから各平均値で引き、XXとYYを求めています。
標準偏差を求める
次に、前項で求めた値を「各状態量の標準偏差で割る」という作業が必要です。
表にすると、以下のとおりです。
・標準偏差を求める
| X | Y | |
|---|---|---|
| データ1 | 10 | 20 |
| データ2 | 11 | 18 |
| データ3 | 9.5 | 22 |
| 標準偏差(std) | 0.62 | 1.63 |
| Xの標準偏差 |
\sqrt{\frac{(10-10.2)^2+(11-10.2)^2+(9.5-10.2)^2}{3}}=0.62
Yの標準偏差
\sqrt{\frac{(20-20)^2+(18-20)^2+(22-20)^2}{3}}=1.63
・標準偏差で割る
| XX | YY | |
|---|---|---|
| データ1 | -0.2/0.62=-0.32 | 0/1.63=0 |
| データ2 | 0.8/0.62=1.29 | -2/1.63=-1.23 |
| データ3 | -0.7/0.62=-1.13 | 2/1.63=1.23 |
コードにすると、以下のとおりです。
std = np.zeros(2)
# 標準偏差で割る
for i in range(2):
std[i] = np.std(x[:,i])
for j in range(3):
xx[j,i] = xx[j,i] / std[i]
・やっていることは、平均値の作業と同じです。「np.mean」が「np.std」になっただけです。
・標準偏差はnp.std()の1行で求められます。これは便利!
相関行列を求める
相関行列は、以下の式で与えられます。
R = \begin{pmatrix}
1&r_{yx}\\
r_{xy}&1
\end{pmatrix}
ただし、$r_{xy}$と$r_{yx}$はxとyの相関係数です。マハラノビス距離を求める際は、逆行列$R^{-1}$を使います。
コードにすると以下のとおりです。
R = np.corrcoef(x.transpose())
invR = np.linalg.inv(R)
ただし、np.corrcoef()に渡す配列は、横長の形にしないといけないため、transpose()で
転置しています。$R^{-1}$は以下のように、求まります。
array([[28. , 27.49545417],
[27.49545417, 28. ]])
これで、マハラノビス距離を求める準備が整いました。
次に、正常データでマハラノビス距離を求めてみます。
マハラノビス距離を求める
試しに、データ1のマハラノビス距離を求めてみます。
| XX | YY | |
|---|---|---|
| データ1 | -0.32 | 0 |
マハラノビス距離は前述したとおり、以下の式で与えられます。
D^2 = \frac{1}{n}\tilde{X}R^{-1}\tilde{X}^{T}
データ1の数値を入れると、以下のとおりです。
D^2=\frac{1}{2}
\begin{pmatrix}
-0.32&0
\end{pmatrix}
\begin{pmatrix}
28&27.495\\
27.495&28\\
\end{pmatrix}
\begin{pmatrix}
-0.32\\
0
\end{pmatrix}
=1.4336
コードで書くと、以下のとおりです。
# MD^2の計算
d0 = np.array([-0.32, 0])
d1 = np.dot(d0,invR)
d2 = np.dot(d1,d0)/2
等確率楕円
グラフで出てくる楕円は「等確率楕円」と呼ばれ、以下の資料(P2)が参考になります。
http://civilyarou.web.fc2.com/WANtaroHP_html5_win/f90_STAT/dir_SREG/TeX_ellipse.pdf
コードは以下のとおりです。
curve_c = np.zeros((2,51))
low = np.corrcoef(data[:,0],data[:,1])[0,1]
for i in range(div+1):
r = (-2*(1-low**2)*np.log(1-0.95)/(1-2*low*np.sin(i*2*np.pi/50)*np.cos(i*2*np.pi/50)))**0.5
curve_c[0,i] = avg[0] + std[0]*r*np.cos(i*2*np.pi/50)
curve_c[1,i] = avg[1] + std[1]*r*np.sin(i*2*np.pi/50)
・1行目で、楕円カーブの座標が入る箱を用意しています。
・3行目で相関係数を求め、for文以降は参考資料のとおりに計算しています。
Python上達のコツ
・Python上達の近道は、実装して動かしてみることです。ネットには、先人達が書いた素晴らしい
コードがたくさん落ちています。そのコードをいじってデータを使い練習しましょう。
使うデータは、乱数でもフリーのデータでも何でもOKです。
・Pythonのコードを書いて、初めて動かすときは、必ずバグがあると思ってください。
最初は、エラーが出るのが当たり前です。エラーが出なくなっても、print文で
「データ数」や「出力値」を出して、論理的に間違っていないか確認をとってください。
・論理的な確認をとったら、数種類のダミーデータで確認をとってください。
コードは完璧!と思っていても思わぬ見落としがあったりします。
コード全文
ちなみに、コード中の「if name == 'main':」というのは、ここからコードが始まりますよ!という
宣言です。無くても良いですが、見やすさのために書いています。
import numpy as np
import matplotlib.pyplot as plt
divide = 2 #状態量の数
R = np.zeros((divide,divide)) #相関行列
invR = np.zeros((divide,divide)) #相関行列の逆行列
avg = np.zeros(divide) #平均値
std = np.zeros(divide) #標準偏差
make = 0
p = 0.95 #マハラノビス距離p=0.95で2σ
md_sikii = 2.448#MDの閾値95%で2.448
div = 50 #Mt楕円の分割数
def maha(x):
global make, R, invR, avg, std
N, _ = x.shape #Nはデータ数
xx = np.copy(x)
xx = np.array(xx,dtype="float32")
x_return = []
#各状態量から平均値を引く
for i in range(divide):
if make == 0:
avg[i] = np.mean(x[:,i])
for j in range(N):
xx[j,i] = xx[j,i] - avg[i]
#各状態量を標準偏差で割る
for i in range(divide):
if make == 0:
std[i] = np.std(x[:,i])
for j in range(N):
xx[j,i] = xx[j,i] / std[i]
#make=0のときだけ計算
if make == 0:
R = np.corrcoef(xx.transpose())
invR = np.linalg.inv(R)
make = 1
#MD^2の計算
for i in range(N):
d0 = xx[i,:]
d1 = np.dot(d0,invR)
d2 = np.dot(d1,d0)/divide
x_return.append(d2)
return x_return
if __name__ == '__main__':
curve_c = np.zeros((2,div+1))
#正常データの作成
x1 = np.random.normal(1, 0.3, (1, 50))
y1 = np.random.normal(1, 0.3, (1, 50))
x2 = np.random.normal(1.5, 0.3, (1, 50))
y2 = np.random.normal(1.5, 0.3, (1, 50))
#テストデータの作成
test1 = np.array([1.02,1.5])
test1 = test1.reshape((1,2))
test2 = np.array([0.5,2])
test2 = test2.reshape((1,2))
#正常データの形を整える
data = []
data.append(x1)
data.append(x2)
data.append(y1)
data.append(y2)
data = np.array(data)
data = data.reshape(2,100)
data = data.transpose()
print(data.shape)
#単位空間の作成
_ = maha(data)
#テストデータのマハラノビス距離
md_1 = maha(test1)
md_2 = maha(test2)
#楕円のデータ
low = np.corrcoef(data[:,0],data[:,1])[0,1]
for i in range(div+1):
r = (-2*(1-low**2)*np.log(1-p)/(1-2*low*np.sin(i*2*np.pi/div)*np.cos(i*2*np.pi/div)))**0.5
curve_c[0,i] = avg[0] + std[0]*r*np.cos(i*2*np.pi/div)
curve_c[1,i] = avg[1] + std[1]*r*np.sin(i*2*np.pi/div)
#可視化
plt.figure()
plt.subplot(1,2,1)
plt.scatter(x1, y1, c="green", s=50)
plt.scatter(x2, y2, c="green", s=50)
plt.scatter(test1[:,0],test1[:,1],c="m", s=50)
plt.scatter(test2[:,0],test2[:,1],c="red", s=50)
plt.xlabel("T")
plt.ylabel("KN")
plt.plot(curve_c[0],curve_c[1],c="c",label="MD^2=2.448")
plt.legend()
plt.subplot(1,2,2)
plt.bar([1,2], [md_1[0], md_2[0]], align="center")
plt.grid(True)
plt.xticks([1,2], ["Purple", "Red"])
plt.ylabel("MD^2")
plt.grid(True)
plt.show()
コードを実行すると、冒頭で出た散布図と棒グラフが出力されます。