Elixir Axon で学ぶ機械学習 (Livebook)

Axon で、以下のドキュメントに沿って、機械学習を試してみました。有名な MNIST の手書き数字の画像認識です。
Classifying handwritten digits

ちなみに機械学習はGPUパワーなしには無理なので、以下の方法で Livebook の起動を行いました。大変助かりました。
Google Colaboratory 上で Elixir Livebook を動かす（GPUを無料で使う）

Elixir Axon 機械学習記事のまとめ

問題	記事	活性化関数	出力層	損失関数
単回帰	Elixir Nx で学ぶ	-	-	MSE
２値分類	排他的論理和	tanh	sigmoid	binary_cross_entropy
多値分類	手書き数字認識	relu	softmax	categorical_cross_entropy

関連記事
Elixir Nx の基礎 (Livebook) - Qiita
Livebook 事始め (Elixir) - Qiita
【機械学習】誤差逆伝播法のコンパクトな説明　- Qiita

1.訓練データの取得と正規化

1-1. 必要なインストール

Mix.install([
  {:axon, github: "elixir-nx/axon"},
  {:nx, "~> 0.4"},
  {:exla, "~> 0.4"},
  {:req, "~> 0.3.0"}
])

1-2. 訓練データの取得

base_url = "https://storage.googleapis.com/cvdf-datasets/mnist/"
%{body: train_images} = Req.get!(base_url <> "train-images-idx3-ubyte.gz")
%{body: train_labels} = Req.get!(base_url <> "train-labels-idx1-ubyte.gz")

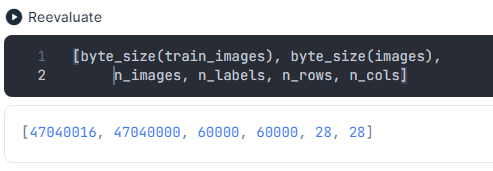
<<_::32, n_images::32, n_rows::32, n_cols::32, images::binary>> = train_images
<<_::32, n_labels::32, labels::binary>> = train_labels

train_images を4個のヘッダー(32ビット)部分と本体の 訓練データ(images) に分解してます。
train_labels も2個のヘッダー(32ビット)部分と本体の 解答ラベル(labels) に分解します。

Elixir では <<>> を使って バイナリ を定義できます。

iex> <<0, 1, 2, 3>>
<<0, 1, 2, 3>>
iex> byte_size(<<0, 1, 2, 3>>)
4

バイナリとはバイトのシーケンスです。

<<_::32, n_images::32, n_rows::32, n_cols::32, images::binary>> = train_images
<<_::32, n_labels::32, labels::binary>> = train_labels

イメージ数もラベル数（解答数）も60000個です。つまり1個の数字で 2828 Byte使用しているので、全体のイメージの byte 数は 2828*60000 = 47040000 となります。画像の1ドットは 0 ～ 255 の整数値で表され、1 byte 使用することに注意してください。画素の色の濃淡を表現しています。

1-3. 訓練データの正規化

images =
  images
  |> Nx.from_binary({:u, 8})
  |> Nx.reshape({n_images, 1, n_rows, n_cols}, names: [:images, :channels, :height, :width])
  |> Nx.divide(255)

Tensor の正規化

• Nx.from_binary(images, {:u, 8})
  binary(=images) から、与えられた型の　1次元 tensor を作ります。
  Nx tensors は unsigned integers (u8, u16, u32, u64) や signed integers (s8, s16, s32, s64)、 floats (f32, f64)、 brain floats (bf16)、 complex (c64, c128) の値を保持します。

• Nx.reshape(x, {n_images, 1, n_rows, n_cols}, names: [:images, :channels, :height, :width])
  1次元 tensor を、意味のある次元の tensor に変形します。ここでは {n_images, 1, n_rows, n_cols} の shape に変形しています。つまり1文字の画像を、 {:channels, :height, :width} = {1, 28, 28} の shape で表していて、その画像 の n_images 個の配列となっているイメージです。

• Nx.divide(255)
  tensor の値は 0～255 の値だから、255 で割ることにより、0～1 の値に変換します。これを 正規化 と呼びます。

何故 MNIST 画像は 1x28x28 テンソルか？
画像は常に3次元マトリックスで表現されます。channels、 width と height です。ここで width と height は 28 です。channel が 1 となります。通常は channel は3色(red, blue, green) を表し 3 なのですが、MNIST 画像は白黒なので 3 channel は必要なく、1 channel で充分です。

この結果得られる、images tensor を可視化してみましょう。

images[[images: 0..4]] |> Nx.to_heatmap()

画面をうまくキャプチャーできないので残念ですが、いい感じに5個の数字のドット絵が表示されます。

1-4. 訓練データのミニバッチ化

images = Nx.to_batched(images, 32)

勾配降下法で学習する場合、何件かの訓練データをグループ化し、一気に勾配計算をやると効率的です。これは ミニバッチ学習法 と呼ばれています。

to_batched(tensor, batch_size, opts \ [])
tensor を tensor batches の Stream に変換します。
tensor の最初の次元 (axis 0) は batch_size で分割されます。

batch_size で割り切れなかった場合の処置は :leftover で指定します。

• :repeat - 最後の batch に、足りない分だけ最初の batch から再利用します。
• :discard - 最後の超過分を切り捨てます。

1-5. labels の one-hot エンコーディングとミニバッチ化

targets =
  labels
  |> Nx.from_binary({:u, 8})
  |> Nx.new_axis(-1)
  |> Nx.equal(Nx.tensor(Enum.to_list(0..9)))
  |> Nx.to_batched(32)

images と同様に、labels も扱いやすいように変換します。
one-hot エンコーディング とは、例えば 3 というスカラー値を、[0, 0, 0, 1, 0, 0, 0, 0, 0, 0] という 3番目だけ 1 で他は全て 0 のベクトルに変換することです。0 番始まりの 3 番目です。

大分細かくなりますが、段階的に変換を追っていきます。

• 最初の変換です。

  labels
  |> Nx.from_binary({:u, 8})

Nx.from_binaryで labels を1次元の tensor に変換します。

#Nx.Tensor<
  u8[60000]
  [5, 0, 4, 1,...,] 

• 次の変換です

  labels
  |> Nx.from_binary({:u, 8})
  |> Nx.new_axis(-1)

Nx.new_axis で size 1 の axis を加えます。 -1 引数なので後ろに axis を加えます。

#Nx.Tensor<
  u8[60000][1]
  [
    [5],
    [0],
    [4],
    [1],
    ---
  ]

• 次の変換です

  labels
  |> Nx.from_binary({:u, 8})
  |> Nx.new_axis(-1)
  |> Nx.equal(Nx.tensor(Enum.to_list(0..9)))

#Nx.Tensor<
  u8[60000][10]
  [
    [0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
    [1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
    ...
  ]

もう少し詳細に見ます。

Nx.tensor(Enum.to_list(0..9))

以下のような tensor になります。

#Nx.Tensor<
  s64[10]
  [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Nx.equal は2つの tensor を比べて、等しい箇所を１に、そうでない個所を０にします。

left = Nx.tensor([[3],[9],[4]])
right = Nx.tensor([0,1,2,3,4,5,6,7,8,9])
Nx.equal(left, right)

以下のように変換されます。

#Nx.Tensor<
  u8[3][10]
  [
    [0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
    [0, 0, 0, 0, 1, 0, 0, 0, 0, 0]
  ]

2. Model の定義

model =
  Axon.input("input", shape: {nil, 1, 28, 28})  # {nil, 1, 28, 28}
  |> Axon.flatten()                             # {nil, 784}
  |> Axon.dense(128, activation: :relu)         # {nil, 128}
  |> Axon.dense(10, activation: :softmax)       # {nil, 10}

教師あり機械学習は、数値を予測する「回帰」というモデルと、どのグループに属するかを予測する「分類」というモデルに大別されます。その中でも分類は、２値分類 と 多値分類 に分けることができます。手書き数字認識の問題は、 多値分類 になります。

コメントはそれぞれの層の output shape です。それが次の層の input shape になります。

Axon.input はネットワークの最初に使われ、ネットワーク層(Layer)を出力します。

Axon.input("input", shape: {nil, 1, 28, 28})
input(name, opts \ [])
ネットワークに input 層 を加える。
name で input 層の名前を与えなければならず、これは複数の input 層がある場合にどの input 層に対する data かを識別するために使われる。
shape は {nil, 1, 28, 28} で (1,28,28) の部分は単体の画像を表しますが、 nil は動的に決定する画像数を表現しています。

以下は、前のネットワークの出力層(Layer)を入力として、次の層(Layer)を出力するものです。引数 x が前の出力層です。

flatten(x, opts \ [])
平坦化された layer をネットワークに加えます。
この layer は、ミニバッチの次元を除いて、全て平坦化されます。つまりこの例で言うと、{nil, 1, 28, 28} の shape が {nil, 784} の shape に変更されます。

Axon.dense(x, 128, activation: :relu)
dense(x, units, opts \ [])
ネットワークに dense 層を加える。dense とは全結合ニューラルネットワークで、１つのニューラルネットワークを定義する。ニューラルネットワークの単位のようなものか。

activation は活性化関数の指定。kernel と bias はレイヤーのパラメータ。units は出力ベクトルの行数。denseの実装は以下の通り。
output = activation(dot(input, kernel) + bias)

dense 層の input shape は x の shape で決まります。
x は (1,28,28)　の tensor を flatten したものだから、784列のベクトルとなる。つまり、ここでは784列のベクトル入力に対して、(784,128)の行列を掛け合わせ、、128列ベクトルの出力を得る。それに bias を足しこみ、最後に activation 関数を適用したものを最終的な出力とする。（列と行、行列と転置行列、結構いい加減に表現しています）

活性化関数 は非線形関数で、ディープラーニングでは線形関数の間に入れて使われます。ここでは ReLU関数（ランプ関数）を用いています。

Dense は通常の全結合ニューラルネットワークレイヤー．
Denseが実行する操作： output = activation(dot(input, kernel) + bias) ただし，activationはactivation引数として渡される要素単位の活性化関数で，kernelはレイヤーによって作成された重み行列であり，biasはレイヤーによって作成されたバイアスベクトルです.(Kerasドキュメントより)

活性化関数 ReLU関数 は以下のように定義されます。

\begin{align}
&y = 0  \qquad x < 0 \\
&y = x  \qquad x >= 0
\end{align}

活性化関数は線形関数の間に挟むことによって全体の学習を効果的にするものですが、この ReLU関数 は特に勾配消失の問題に効果があるとされています。以下引用です。

…最近のディープニューラルネットワークでは、「ReLU」がよく使われるようになっている。というのも、シグモイド関数 や tanh関数 では 勾配消失問題 を解決できなかったが、ReLU では（図2を見ると分かるように「入力が0.0より大きいと、常に1.0が出力される」ことによって） 勾配消失問題 を解決できるようになったからである。
［活性化関数］tanh関数（Hyperbolic tangent function： 双曲線正接関数）とは？:::

Axon.dense(x, 10, activation: :softmax)
直前の dense 層の出力が 128列ベクトルで、それを入力とするこの dense 層では、出力が10行ベクトルなので、(128,10) の行列を掛け合わせる線形変換となります。
活性化関数 に softmax を指定していますが、前の活性化関数の使われ方とは少し違います。ここでは最終出力値を、確率値 を表す0～１の実数値に変換します。推論結果が確率値として得られるわけです。softmax の他に、sigmoid などもあります。

softmax は Model の最終的な出力に使われる活性化関数です。多値分類モデルで使われ、2値分類モデルでは sigmoid が使われます。
softmax では ベクトルの要素 $x_i$ を以下の式で変換します。
$$y_i = \frac{\exp(x_i)}{\sum_{k=1}^n \exp(x_k)} \qquad (i=1,2,...n)$$

$x_i$ は確率値として、0から１までの値をとり、総和は１となります。一番大きな値の項目の確率が最も高い値となります。
以下に softmax による変換例を示します。

\begin{pmatrix}
8.8071 \\
14.1938 \\
12.9936 \\
\end{pmatrix}

=>softmax =>

\begin{pmatrix}
0.0035 \\
0.7650 \\
0.2315 \\
\end{pmatrix}

「PyTorch & 深層学習プログラミング７章　（日経BP）」より

3. 訓練

params =
  model
  |> Axon.Loop.trainer(:categorical_cross_entropy, :adam)
  |> Axon.Loop.metric(:accuracy, "Accuracy")
  |> Axon.Loop.run(Stream.zip(images, targets), %{}, epochs: 10, compiler: EXLA)

機械学習では、繰り返し計算（training loop）を行うことで、Model の dense 層で使われた行列のパラメータを損失がゼロに近づくように、調整していきます。この過程を訓練と呼びます。

これまで獲得した 訓練データ(images)＋解答リスト(targets) と Model （ネットワーク）を用いて、学習を行いまます。

trainer(model, loss, optimizer, loss_scale \ :identity, opts \ [])
Model と 損失関数 とオプティマイザから training loop を作り出します。
ここでは損失関数として categorical_cross_entropy が指定されています。

run(loop, data, init_state \ %{}, opts \ [])
訓練データと解答(labels)を与えてloopを走らせます。
data は Enumerable かまたは Stream で、繰り返しの都度、data batch を提供してくれるもの。

オプションは以下の通り

• :epochs - ループの最大 epoch 数。デフォルト は 1。
• :iterations - 各 epoch 毎の最大繰り返し数。
• :jit_compile? - デフォルト true。
• :debug - ループの過程をトレースするためのデバッグモード。デフォルト false。

compiler: EXLA が無ければ、とても遅いです。

損失関数 交差エントロピー関数 (cross_entropy) Axon.Losses
分類モデルでは損失関数に交差エントロピー関数が使われることが多いようです。２値分類では :binary_cross_entropy、多値分類では :categorical_cross_entropy です。
交差エントロピー誤差をわかりやすく説明してみる
なぜ分類問題の目的関数には交差エントロピーが使われるのか

精度 (Accuracy)
分類モデルでは 精度 を「正解件数／全体件数」として定義することができて、モデルの評価を数値化できます。２値分類モデルでは、予測値が確率値として求められ、0.5 以上が正しいとして 1 と判断する。多値分類モデルでは確率値が最高の分類を正しいとする。

epoch は単位を表します。全訓練データ数/ミニバッチのサイズ数

4. 予測

first_batch = Enum.at(images, 0)

output = Axon.predict(model, params, first_batch)

訓練されたパラメータをもとに、結果を予測します。
ここでは訓練データ自身をテストデータとして使っているので、アレですが、まあ動作確認の意味だけですから。

実行した結果が以下です。とりあえず5個の結果が表示されています。予測値は確率で表現されていますから、それぞれ最も1に近い値が解答となります。

#Nx.Tensor<
  f32[32][10]
  EXLA.Backend<cuda:0, 0.4287185959.1584005128.178388>
  [
    [1.831141302537213e-17, 2.1314743702152114e-17, 2.788575577047925e-13, 0.016425110399723053, 2.6716437079667318e-24, 0.9835748672485352, 4.4600362268452274e-23, 4.170524941561095e-14, 1.6398175635225806e-15, 4.088237723614413e-14],
    [1.0, 1.6728642627921315e-16, 5.3293486956818015e-8, 6.417299061801029e-15, 1.880324350235668e-20, 9.067465677500657e-15, 1.4072107194784689e-12, 4.926563714272025e-13, 1.8360491078894814e-12, 8.877283131682179e-13],
    [1.0514713232046002e-11, 4.384134626889136e-6, 7.727980744220986e-8, 1.8622221542585748e-9, 0.9998115301132202, 1.154940986597408e-11, 2.9517911010433495e-13, 1.8387872842140496e-4, 5.427200733265636e-8, 1.1141140277004524e-7],
    [6.884900288772755e-11, 0.9999977350234985, 9.951911295047466e-9, 1.23654253503247e-9, 3.8443337402327415e-9, 1.4718837260119244e-11, 7.166710801198573e-13, 2.2690628611599095e-6, 3.970355155757943e-9, 6.868552582198087e-16],
    [1.28227966253062e-15, 3.5129577025116987e-10, 3.530791788499202e-14, 3.4387208870612085e-5, 1.5201632095340756e-6, 1.4119769353726497e-8, 4.554542479500676e-17, 4.376623508051125e-8, 8.845394745549129e-7, 0.9999631643295288],
    ...
  ]
>

もともとの解答リストである labels を表示させてみると以下のようになります。

<<5, 0, 4, 1, 9, 2, 1, 3, 1, 4, 3, 5, 3, 6, 1, 7, 2, 8, 6, 9, 4, 0, 9, 1, 1, 2, 4, 3, 2, 7, 3, 8, 6,
  9, 0, 5, 6, 0, 7, 6, 1, 8, 7, 9, 3, 9, 8, 5, 9, 3, ...>>

最初の解答が 5 です。確かに0.9835748672485352が1に近いです。
2番目の解答は 0 です。1.0 となっておりOKです。
3番目の解答は 4 です。0.9998115301132202でOKですね。
4番目の解答は 1 です。0.9999977350234985でOKですね。
5番目の解答は 9 です。0.9999631643295288でOKです。

他の値は 1.xxx e-9 などとほぼゼロの値を指していることに注意してください。

今回は以上です。