分類問題とは
分類問題とは,データをいくつかのカテゴリに分類するもので,機械学習の代表的な方法の一つです。
購買サイトを例にとってみましょう。
ユーザの購買情報からそのユーザが新商品を買うか買わないかを予測します。
2つのカテゴリ(クラス)に分類することを2値分類と呼びます。
2クラスより多い分類予測については、多クラス分類と呼ばれます。
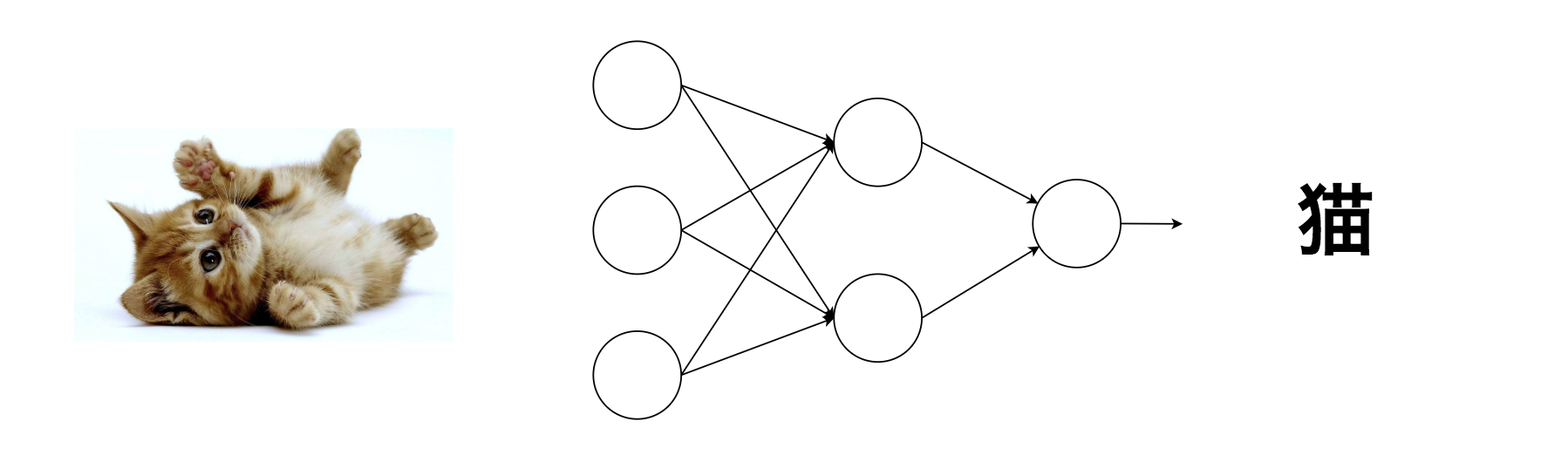
画像に写っている物の判断(画像認識)も多クラス分類問題の1つです。
猫の画像をもとにして、それが猫であると判断するのも分類問題ということですね。
交差エントロピー
2つの確率分布
P(x): 正解データ分布 \\
Q(x): 予測モデル分布
に対して、交差エントロピーは以下で定義されます。
L = - \sum_{x} P(x) \log{Q(x)}
2つの確率分布が似ている分布であるほど、交差エントロピーは小さくなります。
この関数の性質を利用して、機械学習(とくに分類問題)においては目的関数として採用されることが多いです。
本記事では、なぜ目的関数に交差エントロピーが採用されることが多いのか数学的に考察してみます。
交差エントロピーについての詳しい説明は以下が参考になりました。
http://cookie-box.hatenablog.com/entry/2017/05/07/121607
二項分布(ベルヌーイ分布)
分類問題を考察する上で、最も簡単な確率分布である二項分布を例にとります。
P(x_1) = p \;\;\; P(x_2) = 1 - p \\
Q(x_1) = q \;\;\; Q(x_2) = 1 - q \\
箱に赤と白の2色の玉が入っていて、赤を引く確率が
P(赤) = p
白を引く確率が
P(白) = 1 - p
と考えるとわかりやすいですね。
玉が合計10個入っていて、赤が2個、白が8個であるなら
P(赤) = 0.2 \quad P(白) = 0.8
ということです。
さて、このとき目的関数は
\begin{align}
L &= - \sum_{x} P(x) \log{Q(x)} \\
&= - p \log{q} - (1-p) \log{(1-q)}
\end{align}
と展開できます。
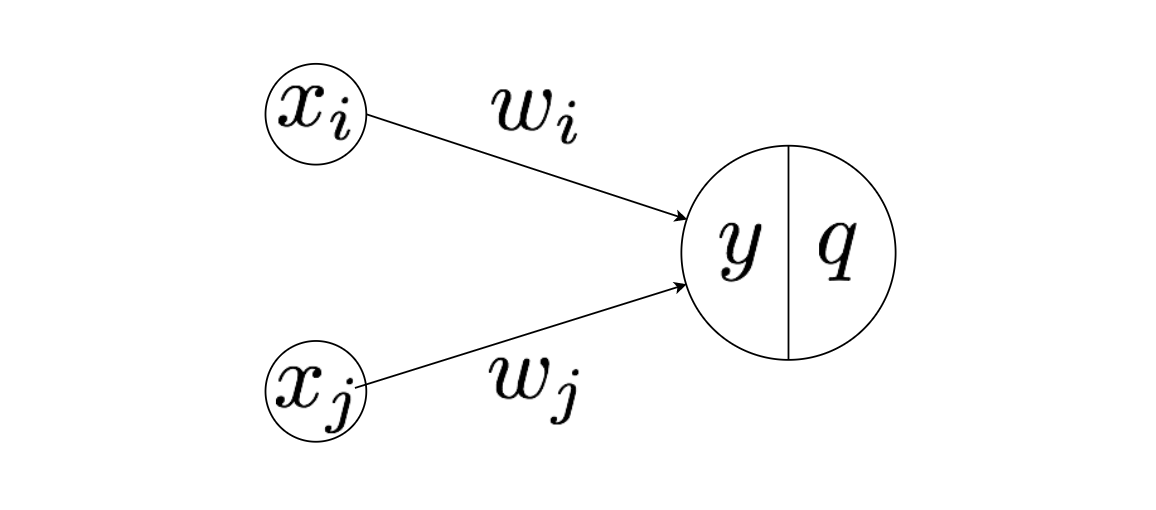
以下のようなシンプルなニューラルネットワークを考えてみましょう。最終的に確率分布 $q$ を求めたいというシナリオを想定してください。先ほどの例をあげると、箱の中身が全くわからないけれど、いくつかの入力データを使用して赤色の玉を引く確率分布をモデルとして構築して結果を予測しようというわけです。
y = \sum_{i} x_i w_i \\
\\
q(y) = \frac{1}{1+e^{-y}} : シグモイド関数
ここで $x_i$を入力、$w_i$を重み、$y$を途中の値、$q$を出力としています。
活性化関数には最も代表的なシグモイド関数を採用しました。
ニューラルネットワークの訓練
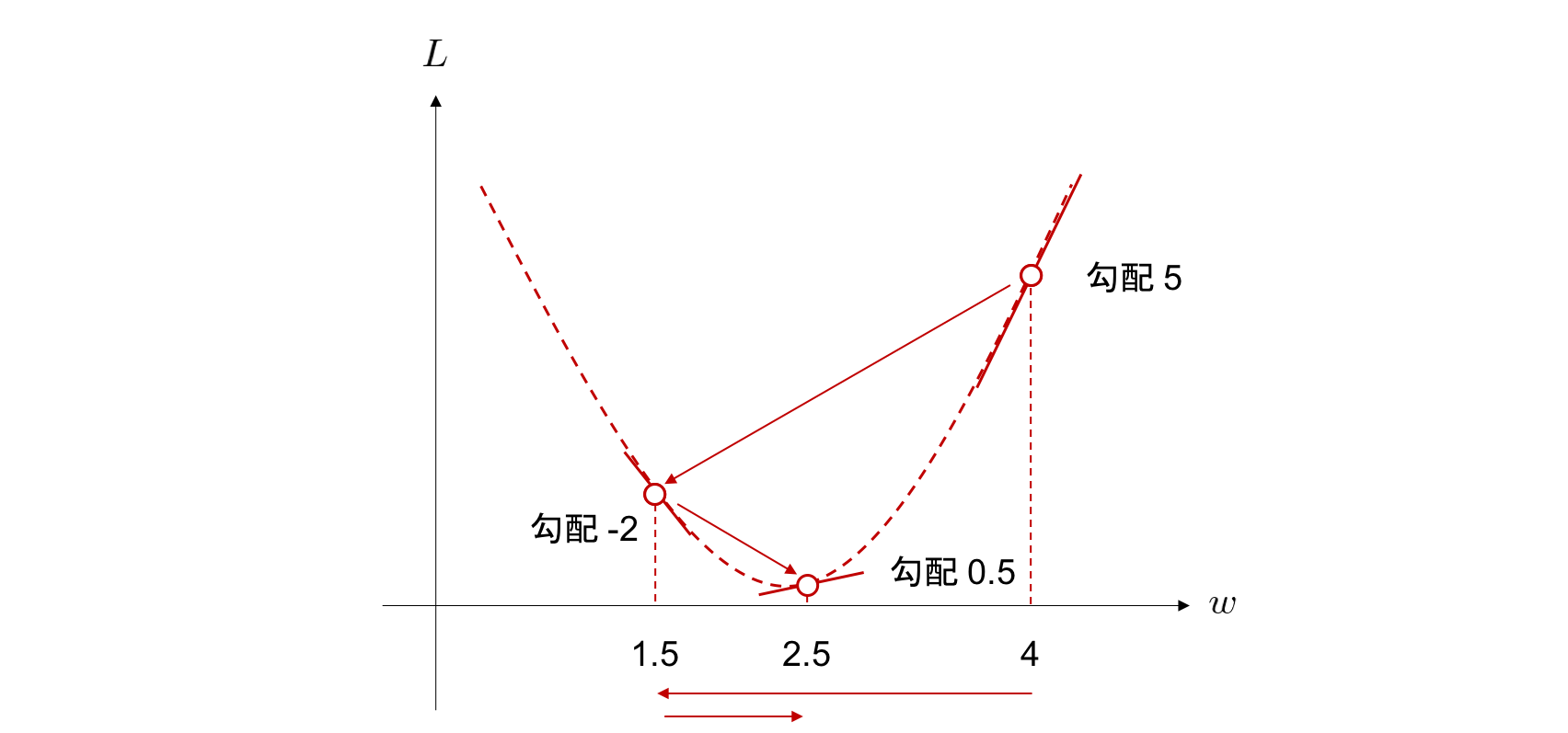
目的関数の値を最小にするようなパラメータの値を求めることで、ニューラルネットワークを訓練します。 最適化アルゴリズムの一つである勾配降下法 (gradient descent) を使用します。
w \leftarrow w - \eta \frac{\partial L}{\partial w}
勾配降下法では学習率×目的関数の勾配を繰りかえし計算し、目的関数の最小値をとる重みを求める手法です。
このあたりの詳しい説明は以下の Chainer Tutorial が非常にわかりやすいです。
https://tutorials.chainer.org/ja/13_Basics_of_Neural_Networks.html
さっそく目的関数を微分していきましょう。
\frac{\partial L }{\partial w_i} = \frac{\partial y}{\partial w_i} \frac{\partial q }{\partial y}\frac{\partial L }{\partial q}
1つ目の微分は
\frac{\partial y}{\partial w_i} = \frac{\partial}{\partial w_i} \sum_i x_i w_i = x_i
2つ目の微分は
\begin{align}
\frac{\partial q }{\partial y} &= \frac{\partial}{\partial y} \frac{1}{1+e^{-y}} \\
&= \frac{\partial u}{\partial y}\frac{\partial}{\partial u} \frac{1}{u} \\
&= -e^{-y} (-u^{-2}) \\
&= \frac{e^{-y}}{1+e^{-y}}\frac{1}{1+e^{-y}} \\
&= \bigl( \frac{1+e^{-y}}{1+e^{-y}} - \frac{1}{1+e^{-y}} \bigr) \frac{1}{1+e^{-y}} \\
&= \bigl( 1-q(y) \bigr) q(y)
\end{align}
3つ目の微分は
\begin{align}
\frac{\partial L}{\partial q} &= \frac{\partial}{\partial q} \{ - p \log{q} - (1-p) \log{(1-q)} \} \\
&= - \frac{p}{q} + \frac{1-p}{1-q}
\end{align}
と計算できるので
\frac{\partial L }{\partial w_i} = x_i (1-q) q \bigl( - \frac{p}{q} + \frac{1-p}{1-q} \bigr) = x_i (q-p)
つまり
p = q
であるとき、目的関数は最小値をとります。
これはいいかえれば正解データの分布と予測モデルの分布が完全に一致することを意味していますね。
まぁ当たり前のことを言っているだけです。
実際に箱の中には赤が8個、白が2個入っていて
赤が80%, 白が20%の確率でしょうと予測しているということです。
分類問題に適用する
さて、分類問題としてもう少しバリエーションを増やしてみましょう。たとえば分類問題ではカテゴリーを 0, 1 で表現することができます。
りんご: [1, 0, 0]
ごりら: [0, 1, 0]
らっぱ: [0, 0, 1]
もう少し汎化していえば
x が所属するクラスの正解が、
t=[t_1, t_2 …t_K]^T
というベクトルで与えられているとします。 ただし、このベクトルは $t_k ; (k=1,2,…,K)$ のいずれか 1 つだけが 1 であり、それ以外は 0 であるようなベクトルであるとします。 これをワンホットベクトル(1-hot vector)と呼びます。
このように分類問題を定義できるようになったので、目的関数は以下のようになります。
L = - \sum_x P(x) \log{ Q(x) } = - \log{ Q(x) }
$Q(x)$ は学習データが教師データと同じになる確率を表しています。
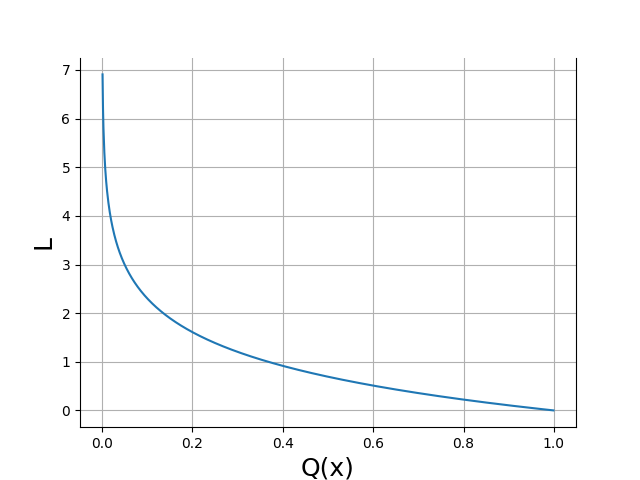
プロットしてみましょう。
勾配降下法では、学習率×目的関数の勾配を繰りかえし計算することで目的関数を最小とする重み $w_i$ を求めるのでした。学習率が極端に高い、あるいは目的関数の勾配が大きければ学習効率が良さそうです。計算のステップ数も少なくなります。
$0 < Q(x) < 1$ に対して、目的関数 $L$ は $Q(x) = 0$ 近傍で急激に減少することがわかります。
このことから教師データと学習結果が違いすぎる場合、1 Stepあたりの減少量が大きいと解釈できます。
分類問題では交差エントロピーを目的関数に選ぶと、計算効率が良いのですね。
実際に Chainer や Pytorch などのライブラリを使っていると忘れてしまいがちですが
基礎的な理論を忘れないように振り返るのも良いですね。勉強になりました。
参考
https://mathwords.net/kousaentropy
https://water2litter.net/rum/post/ai_loss_function/
http://yaju3d.hatenablog.jp/entry/2018/11/30/225841
https://avinton.com/academy/classification-regression/