【機械学習】誤差逆伝播法のコンパクトな説明
【機械学習 誤差逆伝播法】word2vecメモ (1)
【機械学習 誤差逆伝播法】word2vecメモ (2)
※公式の番号は、上記の記事間で共通です。
Deep Learningの基本を勉強するためにまず、「ゼロから作るDeep Learning」(以下、「ゼロから本」)を読むのはもはや定番になっているといえるでしょう。とても丁寧に解説されていてわかりやすいです。ところでDeep Learningの基本原理は驚くほどにシンプルなものですが、その中でも誤差逆伝播法はダントツで複雑に思えます。誤差逆伝播法は、一言で言えば、損失関数をゼロに近づけるために必要なパラメータの勾配(偏微分値)を、効率的に求める計算方法です。
残念なことに「ゼロから本」でも誤差逆伝播法の説明だけがわかりにくいと感じました。計算グラフというものを導入して視覚的にわかりやすくという趣旨の説明だとは思いますが、まず計算グラフというのがハードルでした。ニューラルネットワークの計算の流れをグラフで表記したもので、行列計算や活性化関数などの計算をそれぞれグラフのノードで表現しています。各ノードを注視することで、それぞれの計算を局所化して調べることができます。勾配の計算はグラフを逆の流れでたどることで得られ、それぞれのノードの計算の偏微分も局所的な計算でえられる。説明も局所的なもので行える、というものですが、どうもしっくりきませんでした。私にとってはブログ「頭の中に思い浮かべた時には」の記事の方がわかりやすかったです。こちらは計算グラフは使わずに、厳密な偏微分計算だけで説明してあります。(このブログは、誤差逆伝播法を明晰にわかりやすく説明してあり、お勧めです。)
ただし、「ゼロから本 2」を読むにあったって、計算グラフの説明にも慣れておこうと思い、「ゼロから本 2」の誤差逆伝播法の説明を、私なりに整理してみました。計算グラフの利点は局所的な説明ですので、いろいろな計算(レイヤー)を追加したり、変更したりしても、柔軟に対応できる点にあると思われます。ここではポイントだけの整理です。それが以下の記事です。用語や行列計算の表現はできるだけ本に合わせました。「ゼロから本」の誤差逆伝播法の説明で迷子のなったような気分になったら、補完の意味で読んで頂ければと思います。
また記事の中では特にベクトルや行列の次元は明記していません。今回の議論の中では、特に次元は特定する必要がないと感じたし、記述が少し簡素化されるからです。(今回の話には関係ありませんが、deep learningの世界ではテンソルの階数のことを次元と呼ぶ悪習があるようで、混乱を招きます。何故、階数といわないのだろう?)
【追記 2018/09/04】計算グラフの行列計算が詳細に示されている記事を発見しました。
Pythonと機械学習/行列演算と計算グラフ
1.合成関数の偏微分の公式と誤差逆伝播法
まず誤解を恐れずに言えば、ニューラルネットの出力Yはn個のパラメータを取る関数として見ることができます。
Y = f(w_1,w_2,...w_n)\\
次にLoss関数(損失関数)をLを用いて、この推論値Yと教師データTとの誤差を測ります。
L(Y,T)=L(f(w_1,w_2,...w_n),T) \tag{1-1}
Deep Learningの学習においては、Lの値がゼロになる(近づく)ようにパラメータを決めたいわけです。この時以下のような勾配(偏微分のベクトル)が、Lの極大値の方向を指し示すベクトルであることが、ベクトル解析の分野で知られているところです。ですから現在のパラメータの地点から勾配の逆方向にパラメータを更新すれば、Lは限りなくゼロに近づいて行くことが期待できます。つまりパラメータ(W)から勾配(xΔ)を引いて更新します。Δは学習率と呼ばれ、非常に小さい値(0.01とか)をとればよいことが知られています。このようにすればWは勾配と逆方向に少しだけズレることになります。
\begin{align}
&勾配 \equiv \frac{\partial L}{\partial W} \equiv
\begin{pmatrix}
\frac{\partial L}{\partial w_1} & \frac{\partial L}{\partial w_2} &...& \frac{\partial L}{\partial w_n} \tag{1-2}\\
\end{pmatrix}\\
\\
&パラメータの更新は以下の式で表されます。\\
&W = W - \frac{\partial L}{\partial W} \times Δ\\
\end{align}
勾配を求めるためには、解析学で言う導関数を求める必要はなく、数値微分を使います。任意のパラメータを一つ取り、小さな値だけずらして、Lの値を再計算し、傾きを求める方法です。詳細は「ゼロから本」を参照してください。但しこの勾配の求め方をそのまま実行すると大きなCPUパワーを必要とし、現実的ではありません。
この問題を解決するために誤差逆伝播法が考え出されました。(1-1)のような抽象的な式を眺めるのではなく、具体的なニューロンネットワークを眺めることによって誤差逆伝播法が理解できます。誤差逆伝播法は、ニューロンネットワークの逆方向に合成関数の偏微分の公式を当てはめていくことで、勾配の計算を効率的に行う方法です。
最後に合成関数の偏微分の公式の復習です。
\begin{align}
&aを変数b1,b2,b3の関数とします。\\
&b1,b2,b3を変数cの関数とします。\\
&\frac{\partial a}{\partial c} = \sum_{k=1}^{3} \frac{\partial a}{\partial b_k} \frac{\partial b_k}{\partial c} \tag{1-3}
\end{align}
公式(1-3)は誤差逆伝播法そのものと言えます。このことは「3.局所的な計算」で説明することになります。
以下、誤差逆伝播法を「2.計算グラフの大局」と「3.局所的な計算」の2つの観点から眺めてみたいと思います。
2.計算グラフの大局
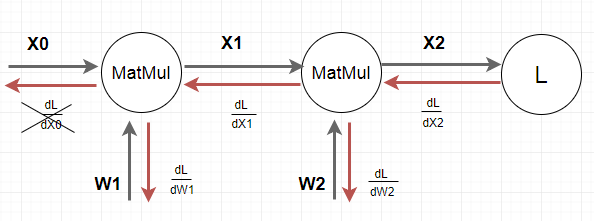
MatMulノードはMatrix Multiplyの略で行列積を行うノードです。以下のネットワーク(計算グラフ)を考えます。最初に2つのMatMulノードがあり、最後にLost関数 L が配置されたネットワークになっています。話を簡単にするために、活性化関数やバイアスは無視していることに注意してください。計算グラフは計算を局所化してみることに特徴がありますが、全体像がわからないと局所の意味も不明になってしまいます。まず大局として全体像を示しておきます。(注意 図の中でdL/dX1等の微分記号を使っています。これはフォントの問題でこう書きましたが、偏微分に置き換えて読んでいただければと思います。)
\begin{align}
&グラフの黒い線が前向き(Forward)の推論ラインです。\\
&前向きに、行列計算(パラメータWによる線形計算)を行い、\\
&出力(X1,X2)を生み出していくラインです。\\
\\
&X0:入力データベクトル\\
&X1=X0 \times W1 \qquad X2=X1 \times W2\\
\\
\\
&(例)行列計算\\
&\begin{pmatrix}
y_{1} & y_{2} & y_{3}
\end{pmatrix}
=
\begin{pmatrix}
x_{1} & x_{2}
\end{pmatrix}
\times
\begin{pmatrix}
w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23}
\end{pmatrix}
=\\
&\begin{pmatrix}
x_1 w_{11} + x_2 w_{21} & x_1 w_{12} + x_2 w_{22} & x_1 w_{13} + x_2 w_{23}
\end{pmatrix}
\\ \\
&i.e. 以下のように成分で記述できます。 \\
&y_i = \sum_k w_{ki}x_k \tag{2-1}\\
\\
\\
\\
\\
&グラフの赤い線が後ろ向き(Backward)の誤差逆伝播法ラインです。\\
&後ろ向きに、合成関数の偏微分公式を用いて、前ノードの偏微分値を再利用し、\\
&パラメータWの勾配を求めていくラインです。\\
\\
&まず\frac{\partial L}{\partial X2}を計算します。\\
&例えば L が2乗誤差の時はベクトルX2の成分で以下のように示せます。\\
&(これは解析的に導関数を解くことで求めます。)\\
&\frac{\partial L}{\partial x2_i} = x2_i - t_i (、t_iは教師データ) \tag{2-2}\\
\\
\\
&次に\frac{\partial L}{\partial X2}を使って\frac{\partial L}{\partial W2}と\frac{\partial L}{\partial X1}を求めます。 \tag{2-3}\\
\\
\\
&最後に\frac{\partial L}{\partial X1}を使って\frac{\partial L}{\partial W1}を求めます。\tag{2-4}\\
\\
&\frac{\partial L}{\partial X0}はもうこれ以上前の層がないので計算不要です。
\\
\\
&(2-3)と(2-4)は同じ手順で計算することができますが、\\
&詳細な計算手順を「3.局所的な計算」で示すことにします。\\
\\
\\
&最終的には\frac{\partial L}{\partial W1}と\frac{\partial L}{\partial W2}で、パラメータのW1とW2を更新します。
\\
\\
\\
\end{align}
3.局所的な計算
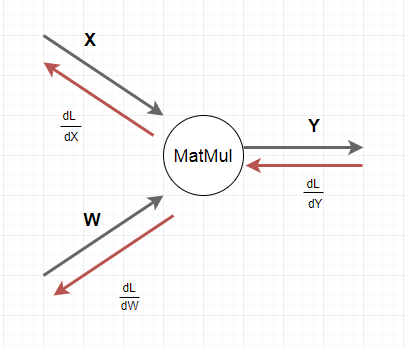
ここでは1個のMatMulノードに注視します。「ゼロから本2」にあわせて少し記号を変えます。ノードの入力をX、出力をYとします。また行列計算を明確にするために、行列やベクトルは成分表示で行います。
\begin{align}
&ひとつ前の\frac{\partial L}{\partial Y}がわかっていれば、\frac{\partial L}{\partial X}と\frac{\partial L}{\partial W}が計算できることを示します。\\
\\
&仮定:\frac{\partial L}{\partial y_i} が既に計算済みである。\\
\\
&目標:(1)\frac{\partial L}{\partial w_{i,j}}と(2)\frac{\partial L}{\partial x_i}を求める。\\
\\
&(1)\frac{\partial L}{\partial w_{ij}}を求めます。\\
&式(2-1)によりy_i = \sum_l w_{li}x_l ですから、w_{ij}に依存する y は y_j だけで、\\
&それ以外は微分するとゼロになります。つまり式(1-3)から以下が成り立ちます。\\
&\frac{\partial L}{\partial w_{ij}} =
\sum_k\frac{\partial L}{\partial y_k} \frac{\partial y_k}{\partial w_{ij}} =
\frac{\partial L}{\partial y_j} \frac{\partial y_j}{\partial w_{ij}}=
\frac{\partial L}{\partial y_j} x_i \tag{3-1}\\
\\
&∴\frac{\partial L}{\partial W} = X^T \times \frac{\partial L}{\partial Y} \tag{3-2}
\\
\\
\\
&(2)\frac{\partial L}{\partial x_i}を求めます。\\
&式(2-1)によりy_k = \sum_l w_{lk}x_lですから、\frac{\partial y_k}{\partial x_i}=w_{ik}となります。\\
&式(1-3)から以下のように計算できます。\\
\\
&\frac{\partial L}{\partial x_i} =
\sum_k \frac{\partial L}{\partial y_k} \frac{\partial y_k}{\partial x_i} =
\sum_k \frac{\partial L}{\partial y_k} w_{ik} \tag{3-3}\\
\\
&∴\frac{\partial L}{\partial X} = \frac{\partial L}{\partial Y} \times W^T \tag{3-4}
\\
\\
\\
\end{align}
4.出力層の逆伝番値
大局のグラフにおける出力層の逆伝番値 $\frac{\partial L}{\partial X2}$ を見てみましょう。これは逆伝搬の始まりとなる計算結果であり、前の結果を利用することなく導かれるものです。前の結果が無いので当然ですが。結果だけですが、出力層の3パタンにおいて、「ゼロから本2」では以下のように示されています。
\begin{align}
&(1)シグモイド関数 + 交差エントロピー誤差\\
&(2)ソフトマックス関数 + 交差エントロピー誤差\\
&(3)恒等関数 + 2乗和誤差\\
\\
&以上の3パターンについて逆伝番値は全て同じで、\\
&教師データをT、出力層のベクトルをあらためてY(=X2)と書けば、\\
\\
&\frac{\partial L}{\partial Y} = Y - T \tag{4-1}\\
\\
&となります。\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}
以上です。これで計算グラフによる誤差逆伝播法の説明が、次の2点において、なんとなくわかったような気がします。一つ目は、計算グラフの全体像をみて、誤差逆伝播法の計算の始まりと終わりをキチンと見ることができたこと。二つ目はMatMulノードでの厳密な計算を示せたこと、です。
最後にくどいようですが、「ゼロから作るDeep Learning」と「ゼロから作るDeep Learning 2」を読まれることをお勧めします。そこにはMatMul以外のノードやミニバッチを考慮した計算方法が明確な形で示されています。