【機械学習 誤差逆伝播法】word2vecメモ (1)

【機械学習】誤差逆伝播法のコンパクトな説明
【機械学習 誤差逆伝播法】word2vecメモ (1)
【機械学習 誤差逆伝播法】word2vecメモ (2)

※公式の番号は、上記の記事間で共通です。

　本記事は「ゼロから作るDeep Learning２」（以下「ゼロから本２」）のword2vec（３章）の読書メモです。3章ではword2vecのCBOWモデルをMatMulノードを使って実装してあります。MatMulノードは1章でPython(Numpy)プログラムとして示されています。Pythonプログラムは具体的なものですが、数学的にどのような計算が行われているかが見えにくい部分もあります。ここでは計算メモとして、その辺をもう少し明らかにしたいと思います。

　1章のMatMulノードについては、「【機械学習】誤差逆伝播法のコンパクトな説明」 にまとめてあります。そこで示した公式を、必要に応じて公式番号で参照します。ご参照ください。

一般的なMatMulノードの勾配

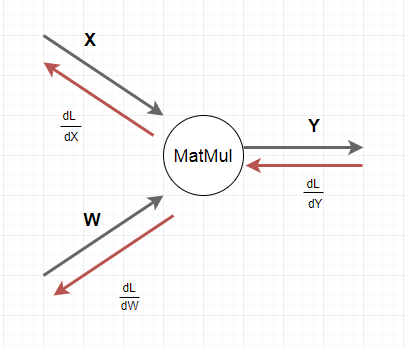
　まずMatMulノードの勾配の計算（誤差逆伝播法）についての復習です。

\begin{align}
&一般的なMatMulノードにおいて、勾配は以下の計算式で求めることができます。\\
\\
&\frac{\partial L}{\partial W} = X^T \times \frac{\partial L}{\partial Y} \tag{3-2}\\
\\
&\frac{\partial L}{\partial X} = \frac{\partial L}{\partial Y} \times W^T \tag{3-4}\\
\\

&\qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}

入力層の勾配

　CBOWモデルにおいては、コンテキストを入力します。これは２つのone-hotベクトルです。Forward計算（推論）において、one-hotベクトルと行列$W_{in}$との掛け算は、行の抜き出しに他なりません。Backward(誤差逆伝播法)においては、前記事で示した公式に従って計算できます。

\begin{align}
\\
&CBOWモデルの入力ベクトルは２つあります。\\
&X_1=(1　0　0　0　0　0　0)\\
&X_2=(0　0　1　0　0　0　0)\\
\\
&W_{in}を以下のようにします。\\
\\
&W=W_{in}=
\begin{pmatrix}
w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23} \\
w_{31} & w_{32} & w_{33} \\
w_{41} & w_{42} & w_{43} \\
w_{51} & w_{52} & w_{53} \\
w_{61} & w_{62} & w_{63} \\
w_{71} & w_{72} & w_{73} \\
\end{pmatrix}
\\
\\
\\
&Forwardの計算です。\\
\\
&Y_1 = X_1 W_{in} = (w_{11}　w_{12}　w_{13})\\
&Y_2 = X_2 W_{in} = (w_{31}　w_{32}　w_{33})\\


\\
\\
\\
&Backwardの計算です。\\
\\
&CBOWモデルの特性から \frac{\partial L}{\partial Y_1} =\frac{\partial L}{\partial Y_2}なので、\\
&\frac{\partial L}{\partial Y_1} =\frac{\partial L}{\partial Y_2} = (l_1　l_2　l_3)とした時、\\
\\
&X_1ラインは以下のようになります。\\
\\
&\frac{\partial L}{\partial W_{in}} =
\begin{pmatrix}
l_1 & l_2 & l_3 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{pmatrix}
\qquad \qquad  \qquad ∵公式(3-2)
\\
\\
&X_2ラインは以下のようになります。\\

&\frac{\partial L}{\partial W_{in}} =
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
l_1 & l_2 & l_3 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{pmatrix}
\qquad \qquad  \qquad ∵公式(3-2)
\\
\\
&重みはX_1とX_2で共有されますので、結局以下のようになります。\\
\\
&\frac{\partial L}{\partial W_{in}} =
\begin{pmatrix}
l_1 & l_2 & l_3 \\
0 & 0 & 0 \\
l_1 & l_2 & l_3 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{pmatrix}
\\
&\qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad \qquad  \qquad \qquad  \qquad \qquad \\
\end{align}

中間層の勾配

　中間層においては、Forwardは単に行列$W_{out}$との掛け算を行います。Backwardも公式に従って計算するだけです。

\begin{align}
\\
&中間層のベクトルです。\\
&X=(x_1　x_2　x_3)\\
\\
&W_{out}を以下のようにします。\\
&W=W_{out}=
\begin{pmatrix}
w'_{11} & w'_{12} & w'_{13}  & w'_{14} & w'_{15}  & w'_{16} & w'_{17} \\
w'_{21} & w'_{22} & w'_{23}  & w'_{24} & w'_{25}  & w'_{26} & w'_{27} \\
w'_{31} & w'_{32} & w'_{33}  & w'_{34} & w'_{35}  & w'_{36} & w'_{37} \\
\end{pmatrix}
\\
\\
\\
&Forwardの計算です。\\
\\
&Y = X W_{out} = \\
&(\sum_{k=1}^3 x_k w'_{1k} \sum_{k=1}^3 x_k w'_{2k} \sum_{k=1}^3 x_k w'_{3k} \sum_{k=1}^3 x_k w'_{4k} \sum_{k=1}^3 x_k w'_{5k} \sum_{k=1}^3 x_k w'_{6k} \sum_{k=1}^3 x_k w'_{7k})\\

\\
\\
\\

&Backwardの計算です。\\
\\

&SoftmaxWithLoss層の勾配を\frac{\partial L}{\partial Y} = (l_1　l_2　l_3　l_4　l_5　l_6　l_7)とした時、\\
&以下のようになります。 \quad where \quad l_i = y_i - t_i  \qquad ∵公式(4-1)\\
\\
&\frac{\partial L}{\partial W_{out}} =
\begin{pmatrix}
x_1l_1 & x_1l_2 & x_1l_3 & x_1l_4  & x_1l_5  & x_1l_6  & x_1l_7 \\
x_2l_1 & x_2l_2 & x_2l_3 & x_2l_4  & x_2l_5  & x_2l_6  & x_2l_7 \\
x_3l_1 & x_3l_2 & x_3l_3 & x_3l_4  & x_3l_5  & x_3l_6  & x_3l_7 \\
\end{pmatrix}
\qquad  ∵公式(3-2)
\\
\\
&\frac{\partial L}{\partial X} = (\sum_{k=1}^7l_kw'_{1k} \sum_{k=1}^7l_kw'_{2k} \sum_{k=1}^7l_kw'_{3k} )
\qquad \qquad  ∵公式(3-4)\\
\\
\end{align}

　以上ですが、このメモを補助として３章を読めば計算が視覚てきに理解しやすくなるのでは？と思います。