Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@riverplus(Kawazoe)

OR-Toolsでしろまるくろまるの問題を自動生成する

Posted at

はじめに

OR-Tools （Operations Research Tools）でパズルを自動生成する話の第4弾です。

第4弾はしろまるくろまるの問題自動生成です。

しろまるくろまるとは

ルールについては こちら を見て下さい。
要約すると次の3点です。

  • 盤面のすべてのマスに、白丸か黒丸を入れる。
  • 白丸および黒丸は、上下左右にひとつながりになる。
  • 同じ色の2×2のかたまりがあってはならない。

例題と解答：

日本で生まれたパズルですが、世界的には「Yin-Yang（陰陽）」という呼び名のほうがメジャーのようです。

ソルバを作る

まずはソルバから。これまでと同様、OR-Toolsでパズルのルールを実装するのですが、今回が一番難しかったです。

白丸と黒丸がひとつながりであるというルールを制約としていかに表現するかが難問です。完成形の盤面においては、白と黒の境界線が盤面を貫く一本の折れ線になることがポイントです。さらに言い換えると、各交差点をマス目に見立てたときに、1から始めて上下左右に増加させながら入れるやり方に対応すると言えます。

さらに今回は、4×4のマス目を全て埋め尽くすことも必要です。これは2×2のかたまり禁止のルールに対応します。

OR-Toolsの変数の制約として表します。白黒の配置を表す二次元配列の変数cellsに加えて、補助変数として、右図の数字を格納する1サイズ小さい二次元配列の変数numbersを用意します。cellsとnumbersの関係は、下図のように、cellsの隣り合う2マスが異なる色ならnumbersの差は1に等しく（水色）、同じ色なら1以外である（緑）と表せます。

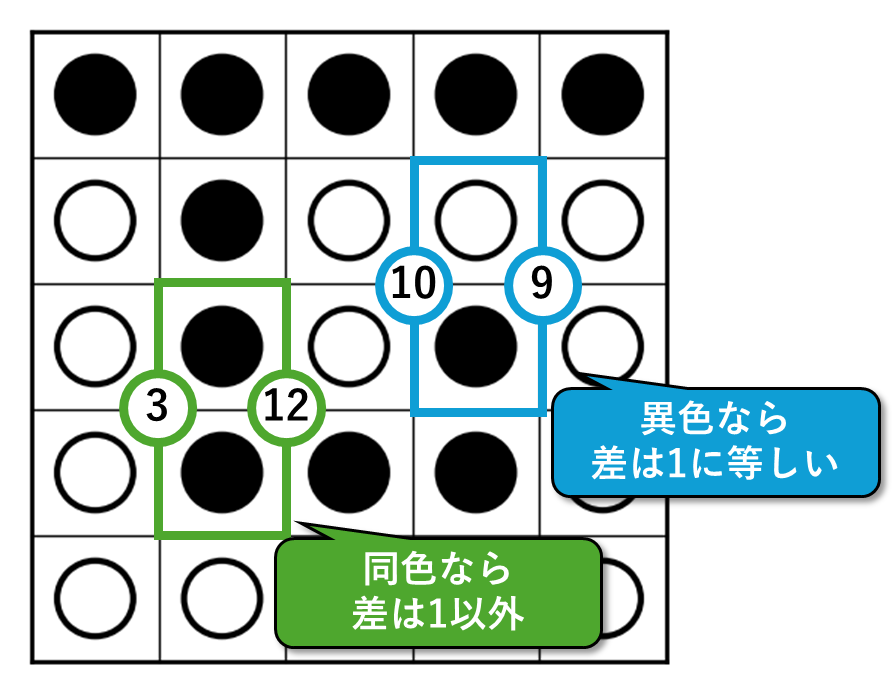
さらにその他の制約として、numbersの2～15の各セルについて、上下左右に±1の値のセルが存在するという制約を追加します。あとは、cellsの四隅のセルがケアされていないため、四隅の2×2の領域が市松模様にならない制約も足します。

以上の制約を用いたソルバを以下に示します。別解ありの場合はmax_count個を上限に全てのパターンを返すようにしています。

from ortools.sat.python import cp_model

def print_board(board):
    for row in board:
        for cell in row:
            c = '.'
            if cell == 1: c = 'O'
            if cell == 2: c = 'x'
            print(c, sep='', end='')
        print()
    print()
    
class Solver(cp_model.CpSolverSolutionCallback):
    def __init__(self, cells, max_count):
        cp_model.CpSolverSolutionCallback.__init__(self)
        self.__cells = cells
        self.__solutions = []
        self.__max_count = max_count

    def OnSolutionCallback(self):
        n = len(self.__cells)
        solution = [[self.Value(self.__cells[row][col]) for col in range(n)] for row in range(n)]
        self.__solutions.append(solution)
        if len(self.__solutions) >= self.__max_count:
            raise TooManySolutionError('')

    def Solutions(self):
        return self.__solutions
    
def solve(board, max_count):
    n = len(board)

    model = cp_model.CpModel()
    cells = [[model.NewIntVar(1, 2, f'cells_{i}_{j}') for i in range(n)] for j in range(n)]
    numbers = [[model.NewIntVar(1, (n-1)*(n-1), f'numbers_{i}_{j}') for i in range(n-1)] for j in range(n-1)]

    # ヒントの値を制約とする。
    for i in range(n):
        for j in range(n):
            if board[i][j] == 0: continue
            model.Add(cells[i][j] == board[i][j])

    # 白黒マス目（cells）と補助変数（numbers）との対応関係を制約で表現する。
    # 隣接するcellsのマス目が同色であれば対応するnumbersのマス目は差が1以上。
    # 異なる色であれば差が1に等しくなる。
    for i in range(n-1):
        for j in range(1, n-1):
            e = model.NewBoolVar(f'e_{i}_{j}')
            model.Add(cells[i][j] == cells[i+1][j]).OnlyEnforceIf(e)
            model.Add(cells[i][j] != cells[i+1][j]).OnlyEnforceIf(e.Not())
            p = model.NewBoolVar(f'p_{i}_{j}')
            model.Add(numbers[i][j-1] - numbers[i][j] == 1).OnlyEnforceIf(p)
            model.Add(numbers[i][j-1] - numbers[i][j] != 1).OnlyEnforceIf(p.Not())
            q = model.NewBoolVar(f'q_{i}_{j}')
            model.Add(numbers[i][j-1] - numbers[i][j] == -1).OnlyEnforceIf(q)
            model.Add(numbers[i][j-1] - numbers[i][j] != -1).OnlyEnforceIf(q.Not())
            model.AddBoolOr([p, q]).OnlyEnforceIf(e.Not())
            model.AddBoolAnd([p.Not(), q.Not()]).OnlyEnforceIf(e)

    for i in range(1, n-1):
        for j in range(n-1):
            f = model.NewBoolVar(f'f_{i}_{j}')
            model.Add(cells[i][j] == cells[i][j+1]).OnlyEnforceIf(f)
            model.Add(cells[i][j] != cells[i][j+1]).OnlyEnforceIf(f.Not())
            p = model.NewBoolVar(f'p_{i}_{j}')
            model.Add(numbers[i-1][j] - numbers[i][j] == 1).OnlyEnforceIf(p)
            model.Add(numbers[i-1][j] - numbers[i][j] != 1).OnlyEnforceIf(p.Not())
            q = model.NewBoolVar(f'q_{i}_{j}')
            model.Add(numbers[i-1][j] - numbers[i][j] == -1).OnlyEnforceIf(q)
            model.Add(numbers[i-1][j] - numbers[i][j] != -1).OnlyEnforceIf(q.Not())
            model.AddBoolOr([p, q]).OnlyEnforceIf(f.Not())
            model.AddBoolAnd([p.Not(), q.Not()]).OnlyEnforceIf(f)

    # 2x2のかたまりがあってはならない。
    directions = [(0, 1), (1, 0), (1, 1)]
    for i in range(n-1):
        for j in range(n-1):
            bools = []
            for di, dj in directions:
                ni, nj = i + di, j + dj
                if ni >= n or nj >= n: continue
                same = model.NewBoolVar(f'same_{i}_{j}_{ni}_{nj}')
                model.Add(cells[ni][nj] == cells[i][j]).OnlyEnforceIf(same)
                model.Add(cells[ni][nj] != cells[i][j]).OnlyEnforceIf(same.Not())
                bools.append(same)
            model.AddBoolOr([b.Not() for b in bools])

    # 四隅は特別なケア。2x2の市松模様があってはならない。
    directions = [(0, 1), (1, 0), (1, 1)]
    for (i, j) in [(0, 0), (0, n-2), (n-2, 0), (n-2, n-2)]:
        bools = []
        for di, dj in directions:
            ni, nj = i + di, j + dj
            if ni >= n or nj >= n: continue
            ichi = model.NewBoolVar(f'ichi_{i}_{j}_{ni}_{nj}')
            if di == dj:
                model.Add(cells[ni][nj] == cells[i][j]).OnlyEnforceIf(ichi)
                model.Add(cells[ni][nj] != cells[i][j]).OnlyEnforceIf(ichi.Not())
            else:
                model.Add(cells[ni][nj] != cells[i][j]).OnlyEnforceIf(ichi)
                model.Add(cells[ni][nj] == cells[i][j]).OnlyEnforceIf(ichi.Not())
            bools.append(ichi)
        model.AddBoolOr([b.Not() for b in bools])

    # 同じ数字は入らない
    model.AddAllDifferent([numbers[i][j] for i in range(n-1) for j in range(n-1)])
    
    # numbersはひとつながり
    directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
    for i in range(n-1):
        for j in range(n-1):
            posi, nega = [], []
            for di, dj in directions:
                ni, nj = i + di, j + dj
                if ni < 0 or nj < 0 or ni >= n-1 or nj >= n-1: continue
                p = model.NewBoolVar(f'p_{i}_{j}_{ni}_{nj}')
                model.Add(numbers[ni][nj] - numbers[i][j] == 1).OnlyEnforceIf(p)
                model.Add(numbers[ni][nj] - numbers[i][j] != 1).OnlyEnforceIf(p.Not())
                posi.append(p)
                q = model.NewBoolVar(f'q_{i}_{j}_{ni}_{nj}')
                model.Add(numbers[ni][nj] - numbers[i][j] == -1).OnlyEnforceIf(q)
                model.Add(numbers[ni][nj] - numbers[i][j] != -1).OnlyEnforceIf(q.Not())
                nega.append(q)
            s = model.NewBoolVar(f's_{i}_{j}')
            model.Add(numbers[i][j] == 1).OnlyEnforceIf(s)
            model.Add(numbers[i][j] != 1).OnlyEnforceIf(s.Not())
            t = model.NewBoolVar(f't_{i}_{j}')
            model.Add(numbers[i][j] == (n-1)*(n-1)).OnlyEnforceIf(t)
            model.Add(numbers[i][j] != (n-1)*(n-1)).OnlyEnforceIf(t.Not())
            u = model.NewBoolVar(f'u_{i}_{j}')
            model.Add(sum(posi) == 1).OnlyEnforceIf(u)
            model.Add(sum(posi) != 1).OnlyEnforceIf(u.Not())
            v = model.NewBoolVar(f'v_{i}_{j}')
            model.Add(sum(nega) == 1).OnlyEnforceIf(v)
            model.Add(sum(nega) != 1).OnlyEnforceIf(v.Not())

            st = model.NewBoolVar(f'st_{i}_{j}')
            model.AddBoolOr([s, t]).OnlyEnforceIf(st)
            model.AddBoolAnd([s.Not(), t.Not()]).OnlyEnforceIf(st.Not())
            model.AddBoolAnd([u, v]).OnlyEnforceIf(st.Not())

    solver = cp_model.CpSolver()
    solution_printer = Solver(cells, max_count)
    try:
        solver.SearchForAllSolutions(model, solution_printer)
    except:
        pass

    return solution_printer.Solutions()

if __name__ == '__main__':

    board = [
        [2, 0, 0, 0, 2],
        [0, 0, 0, 1, 1],
        [1, 0, 1, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
    ]
    sols = solve(board, 10)
    for s in sols: print_board(s)

なおこのコードでは実はnumbersが1→16と16→1の順に並ぶパターンがそれぞれ出力されるため、たとえ唯一解であっても2つの解を持つと判定してしまいます。その点は目をつぶることにしました。

問題の自動生成

次に問題の自動生成です。今回は過去3記事とは異なるアプローチを用います。初めに完成形の盤面を作り、そこからランダムに白丸/黒丸を1個削除し、これをソルバに解かせてみる。もし唯一解であれば、白丸/黒丸をさらにもう1個削除し、再度ソルバに解かせてみる。このように、唯一解が得られなくなるまで削除を繰り返すというアプローチになります。これは数独などのパズルでも自動生成として有効なアプローチです。

以下が生成のコードになります。ごちゃっとしてますがごめんなさい。

def provide(n):
    empty = [[0 for _ in range(n)] for _ in range(n)]
    boards = solve(empty, 1000)
    candidates = [i for i in range(len(boards))]
    print('Generated %d candidates.' % len(candidates))

    k = random.choice(candidates)
    candidates.remove(k)
    board = copy.deepcopy(boards[k])
    points = [(i, j) for i in range(n) for j in range(n)]
    left = n*n
    while len(points) > 0:
        chosen = random.choice(points)
        points.remove(chosen)
        backup = (chosen, board[chosen[0]][chosen[1]])
        board[chosen[0]][chosen[1]] = 0
        
        solutions = solve(board, 3)

        if len(solutions) > 2:
            board[backup[0][0]][backup[0][1]] = backup[1]
        else:
            left -= drop
    
    for row in board:
        for cell in row:
            print(cell, sep='', end='')
        print()
    print()
    for row in solutions[0]:
        for cell in row:
            print(cell, sep='', end='')
        print()
    print()

出力例

こんな結果が出ました。なかなかそれらしい問題が出来ていると思います。



所感

しろまるくろまるの分断禁止は制約として非常に表しにくいルールですが、白黒丸の境界を連番の穴埋めに帰着させることで表現できるようになったのはとても面白いと思いました。

しかし一方で、ソルバの動作がいまいち高速でなく、そのため問題生成にもかなり時間がかかってしまいました。10×10サイズでだいたい1問あたり数分かかってしまいます。有名な手筋を制約として追加してやればもっと高速になるのかな？ この辺は未検証です。

おわりに

OR-Toolsを使って、しろまるくろまるの問題の自動生成を行いました。

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?