はじめに
OR-Toolsでナンバーリンクの問題を自動生成する に続き、OR-Tools (Operations Research Tools)を使ってパズルを自動生成する話です。
今回は、ABCプレースの問題自動生成を行います。
ABCプレースとは
ルールについては Wikipedia をご覧になって下さい。
引用すると次の2点です。
- 各列に、指定された文字を1つずつ記入する(文字が入らないマスもある)。
- 枠外にある文字は、その列で最も辺に近い位置にある文字である。
ソルバを作る
パズル問題の自動生成では、とにかくソルバを作らないと始まりません。
問題のルールをOR-Toolsの制約に翻訳します。特にABCプレースの特徴と言えるのが、「枠外にある文字はその列で最も辺に近い位置にある文字である」というルールです。感覚的にはすぐ理解できるこのルールを、いかにOR-Toolsの制約に翻訳するかというのが考えどころです。
ある列のヒント「X」に対して、辺に近いマスの並びが X, -X, --X, ---X, ‥‥ のいずれかに等しい(-は空マス)、と読み替えることにしました。(もうちょっと利口な方法があるかもしれません。)
もう一つのルールが「各列に、指定された文字を1つずつ記入する」です。全てのセルに文字を入れるのであれば、CpModelのAddAllDifferentという制約がそのまま使えるのですが、このパズルでは空セルがあり得るため、文字ごとにAddExactlyOneで制約を付けます。
以上の制約を用いたソルバのコードを以下に示します。なお、A,B,C,‥‥ の文字を 1,2,3,‥‥ の数字に置き換えています。また別解が存在する場合は最大4万件を得るようにしています。
from ortools.sat.python import cp_model
class TooManySolutionError(Exception):
def __init__(self, message):
self.message = message
super().__init__(self.message)
class SolutionPrinter(cp_model.CpSolverSolutionCallback):
def __init__(self, grid):
cp_model.CpSolverSolutionCallback.__init__(self)
self.grid = grid
self.solutions = []
def OnSolutionCallback(self):
grid = [[self.Value(self.grid[r][c]) for c in range(len(self.grid))] for r in range(len(self.grid))]
self.solutions.append(grid)
if len(self.solutions) > 40000:
raise TooManySolutionError('')
def SolutionCount(self):
return self.solution_count
def solve(clues, n, m):
model = cp_model.CpModel()
# 変数を定義 (各マスに0...Mの値を入れる)
grid = [[model.NewIntVar(0, m, f"cell_{r}_{c}") for c in range(n)] for r in range(n)]
# 1...m がそれぞれ1度ずつ現れるようにする制約
def add_unique_constraints(array):
for k in range(1, m+1):
v = [model.NewBoolVar(f'v_{k}_{i}') for i in range(n)]
for i in range(n):
model.Add(array[i] == k).OnlyEnforceIf(v[i])
model.Add(array[i] != k).OnlyEnforceIf(v[i].Not())
model.AddExactlyOne(v)
for c in range(n):
add_unique_constraints([grid[r][c] for r in range(n)])
for r in range(n):
add_unique_constraints([grid[r][c] for c in range(n)])
# 枠外にある文字はその列で最も辺に近い位置にある文字である制約
def add_line_constraints(array, clue):
if clue == 0:
return
w = [model.NewBoolVar(f'w_{i}') for i in range(n-m+1)]
for k in range(n-m+1):
u = [model.NewBoolVar(f'u_{k}_{i}') for i in range(k+1)]
for i in range(k):
model.Add(array[i] == 0).OnlyEnforceIf(u[i])
model.Add(array[i] != 0).OnlyEnforceIf(u[i].Not())
model.Add(array[k] == clue).OnlyEnforceIf(u[k])
model.Add(array[k] != clue).OnlyEnforceIf(u[k].Not())
model.AddBoolAnd(u).OnlyEnforceIf(w[k])
model.AddBoolOr([b.Not() for b in u]).OnlyEnforceIf(w[k].Not())
model.AddBoolOr(w)
# 上側と下側のヒント
for c in range(n):
add_line_constraints([grid[r][c] for r in range(n)], clues['top'][c])
add_line_constraints([grid[r][c] for r in reversed(range(n))], clues['bottom'][c])
# 左側と右側のヒント
for r in range(n):
add_line_constraints([grid[r][c] for c in range(n)], clues['left'][r])
add_line_constraints([grid[r][c] for c in reversed(range(n))], clues['right'][r])
# ソルバーの作成と解の探索
solver = cp_model.CpSolver()
printer = SolutionPrinter(grid)
# 解を求める (全解を探索)
try:
status = solver.SearchForAllSolutions(model, printer)
except TooManySolutionError as e:
pass
return printer.solutions
if __name__ == '__main__':
n, m = 5, 3
clues = {
'top': [2, 0, 0, 0, 3],
'bottom': [3, 0, 0, 0, 1],
'left': [0, 0, 0, 0, 1],
'right': [0, 0, 0, 3, 2],
}
solutions = solve(clues, n, m)
for row in solutions[0]:
print(row)
問題の自動生成
次に問題の自動生成です。今回は、ヒントをランダムに生成するアプローチを用いることにしました。すなわち、ヒントの数字をランダムに生成して、ソルバに解かせてみる。唯一解が得られればヒントと正答を出力して終了。得られなければ破棄して再トライするというものです。
しかしながら、実際のところ、ランダム生成で唯一解が得られる事はきわめて稀でした。解無しだったり別解ありだったりする場合がほとんどでした。
そこでさらなる工夫を行います。別解ありだった場合に、ヒントの数字を追加することで唯一解に絞り込むことを考えます。
具体例を示します。図のヒントをソルバに解かせてみると、4通りの別解が存在することが分かります。

ここで4通りの別解を注意深く見ると、赤字の位置にヒントを追加してやることで、唯一解に絞り込めることが分かります。

以上のアプローチをコードにしました。追加するヒントの個数ができるだけ少なくなるように工夫しています。ごちゃついたコードなのはごめんなさい。
def random_clue(m):
# 60%の確率で0(ヒントなし)、40%の確率で1~mのいずれかを出力する
rate = 60
options = [i for i in range(m+1)]
weights = [rate] + [(100-rate)/m for i in range(m)]
return random.choices(options, weights=weights, k=1)[0]
def get_clue(array):
for v in array:
if v != 0: return v
return -1
def output(clues, solution):
n = len(solution)
print('top: ', clues[0:n])
print('bottom: ', clues[n:2*n])
print('left: ', clues[2*n:3*n])
print('right: ', clues[3*n:])
print('solution:')
for row in solution:
print(row)
def provide(n, m):
while True:
while True:
clues = {
'top': [random_clue(m) for i in range(n)],
'bottom': [random_clue(m) for i in range(n)],
'left': [random_clue(m) for i in range(n)],
'right': [random_clue(m) for i in range(n)],
}
solutions = solve(clues, n, m)
if len(solutions) > 0: break
# ヒントを追加することで唯一解になる可能性を探る
sol_dict = {}
for sol in solutions:
key = []
key.extend([get_clue([sol[j][i] for j in range(n)]) for i in range(n)]) # top
key.extend([get_clue(reversed([sol[j][i] for j in range(n)])) for i in range(n)])
key.extend([get_clue([sol[j][i] for i in range(n)]) for j in range(n)]) # left
key.extend([get_clue(reversed([sol[j][i] for i in range(n)])) for j in range(n)])
key = tuple(key)
if key not in sol_dict:
sol_dict[key] = []
sol_dict[key].append(sol)
def clue_sub(depth, depth_max, i0, indexes):
if depth == depth_max:
counts = {}
for s in sol_dict.keys():
t = tuple([s[j] for j in indexes])
if t not in counts:
counts[t] = []
counts[t].append((s, indexes))
for k, count in counts.items():
if len(count) != 1: continue
clue, indexes = count[0][0], count[0][1]
sols = sol_dict[clue]
if len(sols) != 1: continue
hint = clues['top'] + clues['bottom'] + clues['left'] + clues['right']
for i in range(len(indexes)):
hint[indexes[i]] = k[i]
output(hint, sols[0])
return True
return False
else:
for i in range(i0, 4*n):
indexes.append(i)
r = clue_sub(depth+1, depth_max, i+1, indexes)
indexes.pop()
if r: return True
return False
for depth_max in range(1, 5):
r = clue_sub(0, depth_max, 0, [])
if r: return
if __name__ == '__main__':
provide(5, 3)
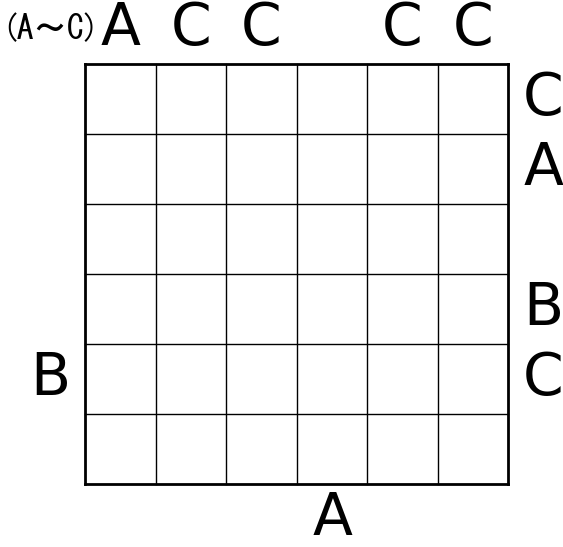
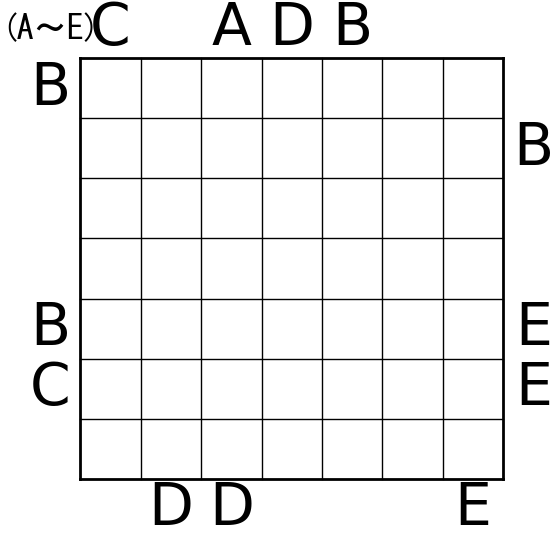
出力例
こんな感じの結果が出ました。
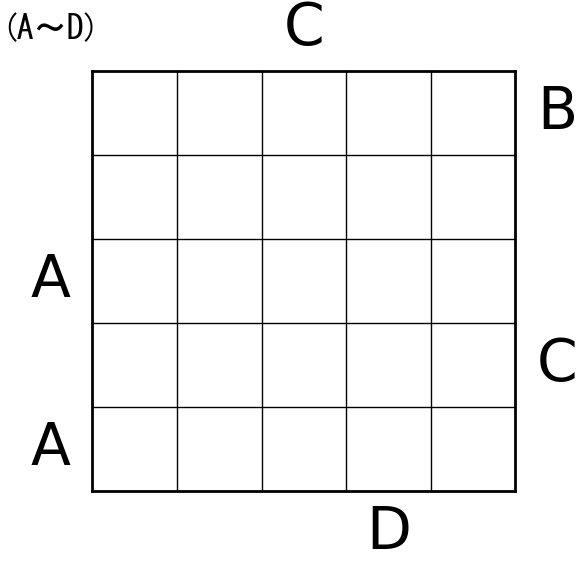
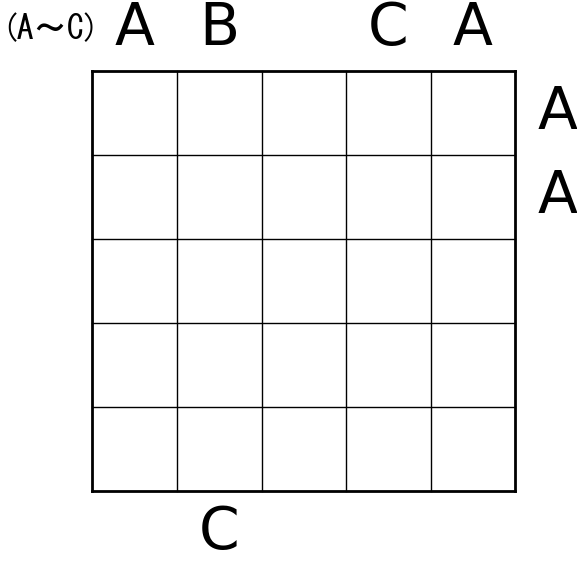
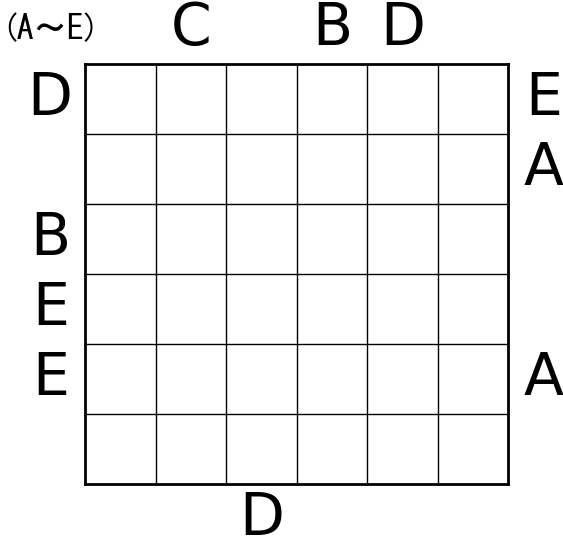
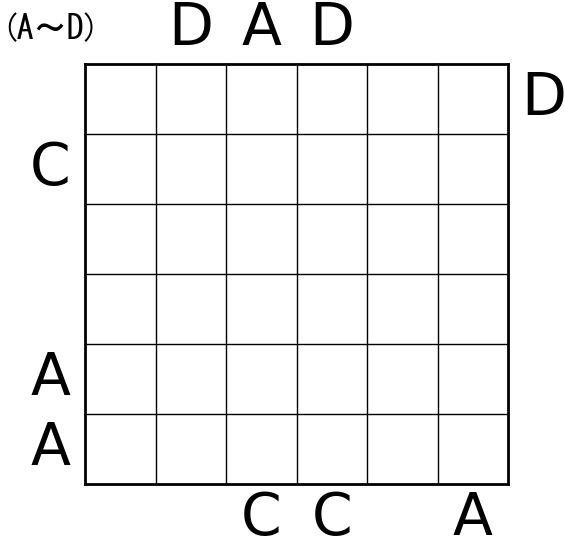

所感
実際に手で解いてみると分かりますが、どの問題もめちゃくちゃ難しいです。いわゆる解き味のようなものは完全無視された形です。あくまで唯一解を持つことが分かっているだけ。
サイズが大きくなると時間がかかります。始めにランダムなヒントでソルバに解かせたときに、解なしだったり、別解が異常に多かったりする場合がほとんどでした。8×8以上のサイズはほぼ無理でした。そもそも問題として成立する配置がレアなのだろうと想像しています。
おわりに
OR-Toolsを使って、ABCプレースの問題の自動生成を行いました。

