はじめに
OR-Tools (Operations Research Tools) は、Googleが開発・提供するオープンソースの最適化ソフトウェアです。この中の一つのモジュールである CP-SAT Solver(Constraint Programming SAT Solver) は、制約充足問題(CSP: Constraint Satisfaction Problem)のソルバを提供しています。
今回、このツールを使って、ナンバーリンクというパズルの問題の自動生成を行います。
ナンバーリンクの問題を解く方に関しては、いくつかの記事を見つけることができました。問題生成についてはQiita内では見当たりませんでした。
ナンバーリンクとは
ルールについては ニコリの解説 をご覧になって下さい。
まずはソルバから作る
パズルを自動生成するには、色々なアプローチの仕方があります。どのようなアプローチを取るにしても、実際に与えられた盤面を解くコードが欠かせません。まずはそのようなコードを作成します。
左図のように、空白セルを0とした2次元配列を入力とし、右図のように、各セルを経路の数字で埋めたものを出力(解)とします。
ソルバは割とシンプルに作れます。以下の制約をOR-Toolsのモデルに与えてやります。未踏のセル(0)があってもよいとすることと、ラインの端点および途中点を制約としてうまく表現することがポイントです。
- 各セルには、0から3までの数字が入る。
- ヒントのあるセルにはその数字が入る。
- ヒントのあるセル(端点)について、その上下左右のセルのうち、そのセルと同じ数字が入るものはちょうど1個(図中青丸)である。
- ヒントのないセル(途中点)について、その上下左右のセルのうち、そのセルと同じ数字が入るものはちょうど2個(図中赤丸)である。
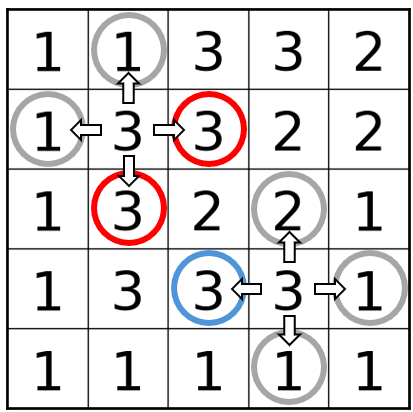
ソルバを作る際に重要なのが、別解を検出できることです。カスタムの解列挙クラスを作成し、CpSolver のコールバック機能を使用します。2個以上の解があると判明した時点で、例外を投げるようにしています。
以下がコードです。
from ortools.sat.python import cp_model
class ManySolutionException(Exception):
def __init__(self, message):
self.message = message
super().__init__(self.message)
class Solver(cp_model.CpSolverSolutionCallback):
def __init__(self, cells):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__cells = cells
self.__solutions = []
def OnSolutionCallback(self):
n = len(self.__cells)
solution = [[self.Value(self.__cells[row][col]) for col in range(n)] for row in range(n)]
if len(self.__solutions) != 0:
raise ManySolutionException('')
self.__solutions.append(solution)
def Solutions(self):
return self.__solutions
def solve(board, m):
n = len(board)
model = cp_model.CpModel()
cells = [[model.NewIntVar(1, m, f'cell_{i}_{j}') for i in range(n)] for j in range(n)]
# ヒントの数字を制約に追加.
for i in range(n):
for j in range(n):
if board[i][j] == 0: continue
model.Add(cells[i][j] == board[i][j])
# 各セルについて, 上下左右で接する4つのセルのうち, そのセルと同じ数字が入るものの個数が
# 1(ヒントの数字が存在するセルの場合)または2(存在しないセルの場合)である制約を追加.
for i in range(n):
for j in range(n):
bools = []
for di, dj in [(0, 1), (1, 0), (0, -1), (-1, 0)]:
ni, nj = i + di, j + dj
if ni < 0 or ni >= n or nj < 0 or nj >= n: continue
e = model.NewBoolVar(f'e_{i}_{j}_{ni}_{nj}')
model.Add(cells[i][j] == cells[ni][nj]).OnlyEnforceIf(e)
model.Add(cells[i][j] != cells[ni][nj]).OnlyEnforceIf(e.Not())
bools.append(e)
a = 2 if board[i][j] == 0 else 1
f = model.NewBoolVar(f'f_{i}_{j}')
model.Add(cells[i][j] != 0).OnlyEnforceIf(f)
model.Add(cells[i][j] == 0).OnlyEnforceIf(f.Not())
model.Add(sum(bools) == a).OnlyEnforceIf(f)
solver = cp_model.CpSolver()
solution_printer = Solver(cells)
try:
solver.SearchForAllSolutions(model, solution_printer)
except ManySolutionException as e:
return []
return solution_printer.Solutions()
if __name__ == '__main__':
problem = [
[0, 1, 0, 3, 2],
[0, 0, 0, 0, 0],
[0, 0, 2, 0, 1],
[0, 0, 0, 3, 0],
[0, 0, 0, 0, 0],
]
solutions = solve(problem, 5)
for row in solutions[0]:
for cell in row:
print(cell, sep='', end='')
print()
print()
問題の自動生成
次に問題の自動生成です。真っ先に思いつくアプローチは、ランダムに数字を置いてみる方法です。それを実際にソルバに解かせて、ちゃんと解ければOK、解ゼロだったり別解ありだったりする場合は、破棄して別の配置を試すというものです。しかしこの方法はうまく行きません。盤面のサイズが大きくなるほど、そのような配置に会う確率は小さくなります。8×8のサイズで、数時間PCをぶん回しても一度も成功せず、という状況でした。
そこで次のアプローチとして有効だったのが、ここでもOR-Toolsを用いるというものです。以下の制約を設けます。ソルバのときと微妙に異なります。問題が満たすべき条件をできるだけ詳しく書き上げた感じです。
- 各セルには1から3までの数字が入る。
- 1から3の各数字について、「ラインの端点となるセル」がちょうど2個ずつ存在する。ラインの端点となるセルとはすなわち、その上下左右のセルのうち、そのセルと同じ数字が入るものがちょうど1個であるようなセル。
- 上記以外のセルはすべて「ラインの途中点となるセル」となる。ラインの途中点となるセルとはすなわち、その上下左右のセルのうち、そのセルと同じ数字が入るものがちょうど2個であるようなセル。そのようなセルが1個以上なくてはならない(ヒントの数字が隣り合うこととなり、問題としてつまらないため)。
- 2×2のかたまり状に同じ数字が入ってはならない。
以下がコードです。
class Generator(cp_model.CpSolverSolutionCallback):
def __init__(self, cells):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__cells = cells
self.__solutions = []
def OnSolutionCallback(self):
n = len(self.__cells)
solution = [[self.Value(self.__cells[row][col]) for col in range(n)] for row in range(n)]
self.__solutions.append(solution)
if len(self.__solutions) >= 1000:
raise ManySolutionException('')
def Solutions(self):
return self.__solutions
def generate(n, m):
model = cp_model.CpModel()
cells = [[model.NewIntVar(1, m, f'cell_{i}_{j}') for i in range(n)] for j in range(n)]
for k in range(1, m+1):
counts1, counts2 = [], []
for i in range(n):
for j in range(n):
is_k = model.NewBoolVar(f'is_{k}_{i}_{j}')
model.Add(cells[i][j] == k).OnlyEnforceIf(is_k)
model.Add(cells[i][j] != k).OnlyEnforceIf(is_k.Not())
# あるセルの上下左右がkに等しいかどうかのboolがboolsに入る。
bools = []
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
for di, dj in directions:
ni, nj = i + di, j + dj
if ni < 0 or ni >= n or nj < 0 or nj >= n: continue
same = model.NewBoolVar(f'same_{k}_{i}_{j}_{ni}_{nj}')
model.Add(cells[ni][nj] == k).OnlyEnforceIf(same)
model.Add(cells[ni][nj] != k).OnlyEnforceIf(same.Not())
e = model.NewBoolVar(f'e_{k}_{i}_{j}_{ni}_{nj}')
model.AddBoolAnd([is_k, same]).OnlyEnforceIf(e)
model.AddBoolOr([is_k.Not(), same.Not()]).OnlyEnforceIf(e.Not())
bools.append(e)
# bools内のtrueの個数が1または2に等しいという制約。
b1 = model.NewBoolVar(f'b>=1_{k}_{i}_{j}')
model.Add(sum(bools) >= 1).OnlyEnforceIf(b1)
model.Add(sum(bools) < 1).OnlyEnforceIf(b1.Not())
b2 = model.NewBoolVar(f'b<=2_{k}_{i}_{j}')
model.Add(sum(bools) <= 2).OnlyEnforceIf(b2)
model.Add(sum(bools) > 2).OnlyEnforceIf(b2.Not())
model.AddBoolAnd([b1, b2]).OnlyEnforceIf(is_k)
model.AddBoolOr([b1.Not(), b2.Not()]).OnlyEnforceIf(is_k.Not())
# 端点であるかどうか(sum(bools) == 1)のboolがcounts1に入る。
edge = model.NewBoolVar(f'edge_{k}_{i}_{j}')
model.Add(sum(bools) == 1).OnlyEnforceIf(edge)
model.Add(sum(bools) != 1).OnlyEnforceIf(edge.Not())
c = model.NewBoolVar(f'c_{k}_{i}_{j}')
model.AddBoolAnd([is_k, edge]).OnlyEnforceIf(c)
model.AddBoolOr([is_k.Not(), edge.Not()]).OnlyEnforceIf(c.Not())
counts1.append(c)
# 途中点であるかどうか(sum(bools) == 2)のboolがcounts2に入る。
both = model.NewBoolVar(f'both_{k}_{i}_{j}')
model.Add(sum(bools) == 2).OnlyEnforceIf(both)
model.Add(sum(bools) != 2).OnlyEnforceIf(both.Not())
d = model.NewBoolVar(f'd_{k}_{i}_{j}')
model.AddBoolAnd([is_k, both]).OnlyEnforceIf(d)
model.AddBoolOr([is_k.Not(), both.Not()]).OnlyEnforceIf(d.Not())
counts2.append(d)
model.Add(sum(counts1) == 2)
model.Add(sum(counts2) >= 1)
# 2x2のかたまりがあってはならない制約を追加
directions = [(0, 1), (1, 0), (1, 1)]
for i in range(n-1):
for j in range(n-1):
bools = []
for di, dj in directions:
ni, nj = i + di, j + dj
if ni >= n or nj >= n: continue
same = model.NewBoolVar(f'same_{i}_{j}_{ni}_{nj}')
model.Add(cells[ni][nj] == cells[i][j]).OnlyEnforceIf(same)
model.Add(cells[ni][nj] != cells[i][j]).OnlyEnforceIf(same.Not())
bools.append(same)
model.Add(sum(bools) != 3)
solver = cp_model.CpSolver()
solution_printer = Generator(cells)
try:
solver.SearchForAllSolutions(model, solution_printer)
except ManySolutionException as e:
pass
return solution_printer.Solutions()
def provide(n, m):
candidates = generate(n, m)
for solution in candidates:
problem = copy.deepcopy(solution)
for i in range(n):
for j in range(n):
c = 0
for di, dj in [(0, 1), (1, 0), (0, -1), (-1, 0)]:
ni, nj = i + di, j + dj
if ni < 0 or ni >= n or nj < 0 or nj >= n: continue
if solution[i][j] == solution[ni][nj]:
c += 1
if c != 1:
problem[i][j] = 0
try:
solutions = solve(problem, m)
except ManySolutionException as e:
continue
if len(solutions) != 1:
continue
print('---')
for row in problem:
for cell in row:
print(cell, sep='', end='')
print()
print()
for row in solutions[0]:
for cell in row:
print(cell, sep='', end='')
print()
print()
if __name__ == '__main__':
provide(5, 3)
generate関数により、有効な盤面の候補(ただし唯一解があるかどうかは保証されていない)を最大1000件生成します。そしてそのそれぞれについて、solve関数により解いてみて、唯一解であれば出力する、という流れです。
出力例
こんな感じの結果が出ました。それっぽくて良い感じ。

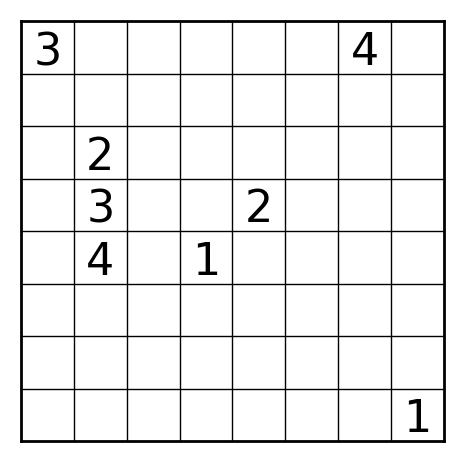
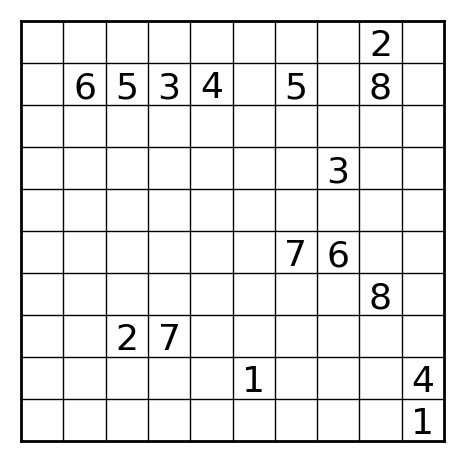
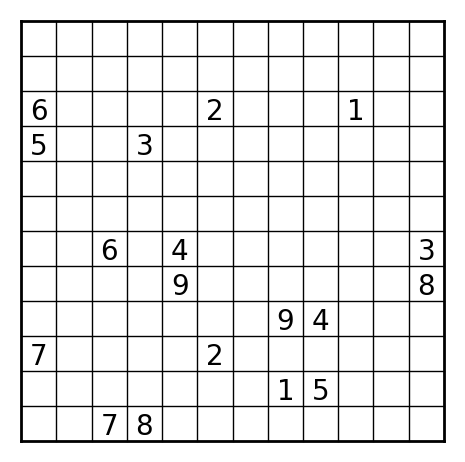
所感
盤面をランダムに生成したときは、唯一解のパターンが得られる確率はきわめて小さかったですが、generate関数で生成するようにするとぐっと上がりました。5×5・ペア数3の場合で、だいたい4割位の成功率でした。
サイズが大きくなるとgenerate関数の生成が非常に遅くなるのが難点でした。12×12あたりになると数時間かかりました。この辺はツールの使い方が下手だったのかもしれません。ひとたび有効な盤面の候補のリストが得られればその後はまあ早いので、大量に作問するのであれば何とか許容範囲内と言えるのですがね。
Infinite Numberlink や mate法を用いた Numberlink 問題自動生成 のページでは、もっとずっと高速に問題生成できているようです。すごいね。
おわりに
OR-Toolsを使って、ナンバーリンクの問題の自動生成を行いました。



