Advent Calendar 16日目の記事 組合せ最適化で美術館を解く
Advent Calendar 18日目の記事 組合せ最適化で四角に切れを解く
これなに
ナンバーリンクを、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。
自分でも試してみたい人は、下記を参考にしてください。
問題
- 各マスには2つ以上の線が入ってはいけません
- 異なる線同士が交わってはいけません
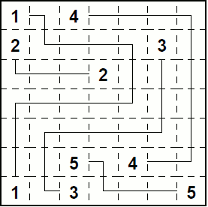
下記は、問題と答えです。
入力パラメータ
dataに始点と終点が入っているとします。
python
import numpy as np
from itertools import product
from pulp import LpProblem, lpSum, value
from ortoolpy import addvars, addbinvar, addbinvars
data = np.array([list(s) for s in """\
1.4....
2....3.
...2...
.......
.......
..5.4..
1.3...5""".splitlines()])
data[data == '.'] = '0'
data = data.astype(int)
Pythonで解く
数理モデルを作成し、解きましょう。
変数
- vr:どのタイプのラインに含まれるか (1)
- vh:水平に出るかどうか (2)
- vv:垂直に出るかどうか (3)
制約
- 始点と終点が指定のラインに含まれること (4)
- 始点と終点は、1本だけ出ること (5)
- 始点終点以外の各マスに接続されるのは、0本か2本 (6)
- 接続したら、両端のタイプは同じになること (7)
python
mx = data.max()
m = LpProblem()
vr = addvars(*data.shape) # (1)
vh = addbinvars(data.shape[0], data.shape[1]-1) # (2)
vv = addbinvars(data.shape[0]-1, data.shape[1]) # (3)
def dirs(i, j):
return ([vh[i][j - k] for k in range(2) if 0 <= j-k < data.shape[1] - 1]
+ [vv[i - k][j] for k in range(2) if 0 <= i-k < data.shape[0] - 1])
for i, j in product(range(data.shape[0]), range(data.shape[1])):
s = dirs(i, j)
if data[i][j]:
m += vr[i][j] == data[i][j] # (4)
m += lpSum(s) == 1 # (5)
else:
m += lpSum(s) == 2 * addbinvar() # (6)
if i < data.shape[0] - 1:
m += vr[i][j] <= vr[i + 1][j] + mx * (1 - vv[i][j]) # (7)
m += vr[i + 1][j] <= vr[i][j] + mx * (1 - vv[i][j]) # (7)
if j < data.shape[1] - 1:
m += vr[i][j] <= vr[i][j + 1] + mx * (1 - vh[i][j]) # (7)
m += vr[i][j + 1] <= vr[i][j] + mx * (1 - vh[i][j]) # (7)
m.solve()
結果の表示
python
print(np.vectorize(value)(vr).astype(int))
>>>
[[1 1 4 4 4 4 4]
[2 1 1 1 1 3 4]
[2 2 2 2 1 3 4]
[1 1 1 1 1 3 4]
[1 3 3 3 3 3 4]
[1 3 5 5 4 4 4]
[1 3 3 5 5 5 5]]
解けていることが確認できます。
以上