Advent Calendar 17日目の記事 組合せ最適化でナンバーリンクを解く
Advent Calendar 19日目の記事 組合せ最適化で数コロを解く
これなに
四角に切れを、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。
自分でも試してみたい人は、下記を参考にしてください。
問題
- 盤面を数字を1つずつ含む長方形に分割します。
- 数字は1マスの面積を1とした長方形の面積になるようにします。
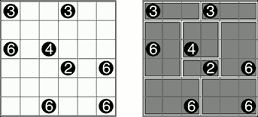
下記は、左が問題で、右が答えです。
入力パラメータ
dataにヒントが入っているとします。
python
import numpy as np
from itertools import product
from pulp import LpProblem, lpSum, value
from ortoolpy import addvars, addbinvars
data = """\
3..3..
......
6.4...
...2.6
......
..6..6""".splitlines()
nw, nh = len(data[0]), len(data)
tgt = [(i, j, int(data[i][j])) for i in range(nh)
for j in range(nw) if data[i][j].isdigit()]
nm = len(tgt)
Pythonで解く
数理モデルを作成し、解きましょう。
変数
- v:各位置が各部屋かどうか (1)
- vl:候補のどれか (2)
制約
- vは1つの部屋のみ (3)
- vlは1つの候補のみ (4)
- vlの1つを選んだら、その位置のその部屋は1 (5)
python
m = LpProblem()
v = np.array(addvars(nh, nw, nm)) # (1)
for i, j in product(range(nh), range(nw)):
m += lpSum(v[i,j]) == 1 # (3)
def make(h, pi, pj, na):
lst = []
for i in range(1, na + 1):
j = na // i
if i * j >= na:
for y in range(i):
if 0 <= pi-y <= nh-i:
ly = range(pi-y, pi-y+i)
for x in range(j):
if 0 <= pj-x <= nw-j:
lx = range(pj-x, pj-x+j)
lst.append([v[dy,dx,h] for dy in ly for dx in lx])
return lst
for h, (i, j, k) in enumerate(tgt):
lst = make(h, i, j, k)
vl = addbinvars(len(lst)) # (2)
m += lpSum(vl) == 1 # (4)
for l, ll in enumerate(lst):
for t in ll:
m += vl[l] <= t # (5)
m.solve()
結果の表示
python
print(np.vectorize(value)(v.dot(range(nm))).astype(int)+1)
>>>
[[1 1 1 2 2 2]
[3 3 4 4 6 6]
[3 3 4 4 6 6]
[3 3 5 5 6 6]
[7 7 7 8 8 8]
[7 7 7 8 8 8]]
解けていることが確認できます。
以上