はじめに
組合せ最適化を使うためのノウハウを説明します。
組合せ最適化を使うコツは、全体像を理解することです。どんな要素があるのか、それらがどのような関係にあるのかを知ることにより、解きたい問題についてアプローチできるようになります。
Python を使うことにより、簡単に、様々な最適化ができます。実際のコードを見ながら、あとで確認しましょう。最初に、身近な最適化の例から見ていきます。
考えてみよう
先日、あなたが実家に帰ると、お土産に野菜を持って帰るよう言われました。東京の野菜は高いので、「儲かった」と喜びましたが、量が多すぎます。せいぜい5kg しか持って帰れないとします。(宅配便は使えないことにしてください) また、野菜は切ったりすると傷むので、そのまま持って帰ることにします。
あなたは「1kg あたりの販売価格の高いものから選んでいこう」と考えました。実は、これは(貪欲法という、高速なよい近似解法ですが) 最適な方法ではありません。本当に最適な方法は、どうすればわかるでしょうか?
全ての可能性を調べれば、最適化な方法はわかります。しかし、全ての野菜の組合せは、野菜の数が増えると爆発してしまい計算できなくなります。
数理最適化を使えば、このような問題を解くことができます。
数理最適化では、数式を使って、問題を数理モデルで表します。先ほどの例は、
| 最大化 | $\sum_i{p_i x_i}$ | $p_i$:販売価格 |
| $\sum_i{w_i x_i} \le 5$ | $w_i$:重さ | |
| $\forall x_i \in \{0, 1\}$ | $x_i$:持って帰るかどうか |
| 連続最適化: | 連続要素のみ |
| 組合せ最適化: | 連続以外の離散要素を含む |
定式化
レッスン1
組合せ最適化では、数理モデルを定式化する。
定式化をするには、3 つの要素を決める必要があります。
| 1. 何を決めたいのか? | 「持って帰る野菜を決めたいです」 |
| 2. どうなるとうれしいのか? | 「持って帰る野菜の販売価格の合計が高くなるとうれしいです」 |
| 3. 守らないといけないことは? | 「持って帰る野菜を5kg 以下にします」 |
| 1. 変数: | $\forall x_i \in \{0, 1\}$ | |
| 2. 目的関数: | $\sum_i{p_i x_i}$ | $\rightarrow$ 最大 |
| 3. 制約条件: | $\sum_i{w_i x_i} \le 5$ |
定式化できるようにするためには、慣れが必要です。今回は、いくつかの例を後で見ることにします。詳しく勉強する場合は、書籍「今日から使える!組合せ最適化」などを参考にしてください。
数理モデルから最適な答えを探すのは、(賢い人が作ってくれた) ツールを使います。このツールのことを最適化ソルバー、略してソルバーとよびます。つまり、問題を(誰でもわかるように)表すだけで、ソルバーを使えば解(答えのこと) を出すことができます。
最近では、このソルバーが使いやすく、性能がたいへんよくなってきました。みんなが、最適化が試せるようになってきているのです。
典型問題
先ほどの例の他に、どんな例があるでしょうか?あなたは実家に帰るときに、webで乗り換え駅を探索したかもしれません。
あなたの家の最寄り駅から、実家の最寄り駅までの最短路(あるいは最安路) を探したい。
これも最適化問題です。最適化問題は、いろいろなところにたくさんあります。でも、問題ごとに定式化するのは、大変ですよね。実は、別々の問題でも、同じ定式化になることがよくあります。そうすると、わざわざ定式化する必要がなくなり、便利ですね。世の中によくある問題を典型問題とよぶことにします。
レッスン2
典型問題を理解する。
関連する典型問題を集めて、典型問題クラスという枠組みを作ります。典型問題クラスは、7 つあります。典型問題は、よく使われるものを厳選しました。
| 典型問題クラス | 典型問題 |
| グラフ・ネットワーク問題 | 最小全域木問題 |
| 最大安定集合問題 | |
| 最大カット問題 | |
| 最小頂点被覆問題 | |
| 最短路問題 | |
| 最大流問題 | |
| 最小費用流問題 | |
| 経路問題 | 運搬経路問題 |
| 巡回セールスマン問題 | |
| 集合被覆・分割問題 | 集合被覆問題 |
| 集合分割問題 | |
| スケジューリング問題 | ジョブショップ問題 |
| 勤務スケジューリング問題 | |
| 切出し・詰込み問題 | ナップサック問題 |
| ビンパッキング問題 | |
| n次元パッキング問題 | |
| 配置問題 | 施設配置問題 |
| 容量制約なし施設配置問題 | |
| 割当・マッチング問題 | 2次割当問題 |
| 一般化割当問題 | |
| 最大マッチング問題 | |
| 重みマッチング問題 | |
| 安定マッチング問題 |
野菜の選び方はナップサック問題、乗り換え駅探索は、最短路問題といいます。典型問題は、よく研究もされているので、多くの場合、効率的な解法があります。あるいは、定式化がされているので、すぐ解くことができます。あとで、やってみましょう。ここで、あげている全ての典型問題の実行例は、典型問題と実行方法をご覧ください。
汎用問題
最近、私がやっているコンテナの仕事のお話しをします。
世界中の人たちが、いろいろなものを安く買えるのはコンテナ輸送のおかげです。中国などで生産したものを日本やアメリカやヨーロッパに、大量に安く運べるからです。でも、空のコンテナが、どんどんたまります。また中国に戻さないといけません。いつ、どこからどこに戻すかを決めるのが、最小費用流問題になります。ところが、最小費用流問題で表せない制約条件もあります。1 つが、カボタージュとよばれるものです。カボタージュというのは、国内のみの輸送を自国業者のみに規制することです。
典型問題で対応できない場合は、数理モデルをそのまま扱います。数理モデルで表された問題を汎用問題とよびます。典型問題は、汎用問題として見ることもできます。汎用問題は、典型問題より汎用的な分類になります。
レッスン3
汎用問題を理解する。
汎用問題には、何があるのでしょうか?
汎用問題の違いは、変数や目的関数や制約の違いによります。汎用問題が異なると、解法(アルゴリズム)が異なります。この解法の種類によって、解きやすさが全く違います。また、汎用問題ごとにソルバーも異なることがあります。なるべく、簡単に解ける汎用問題に持って行けるかが、重要になります。汎用問題は、親子関係になります。

全ての最適化問題は、非線形最適化問題です。なぜ、わざわざ非線形最適化というのでしょうか?それは、線形最適化問題を非線形最適化として扱うのは非効率的だからです。非線形最適化という言葉には、非線形な目的関数か非線形な制約条件があることを暗黙に示唆しています。
線形最適化問題
汎用問題で最も解きやすいのは、線形最適化問題です。最小費用流問題や最短路問題も線形最適化問題です。変数が連続変数で、目的関数と制約条件が線形(1 次式) で表される問題です。これは、かなり大きな問題でも解けるようになってきました。
混合整数最適化問題
目的関数と制約条件は線形ですが、変数の中に(値が整数しか許されない)整数変数を含む問題を混合整数最適化問題とよびます。ナップサック問題も混合整数最適化問題です。
実務でよく現れる問題で、私の扱っている問題の多くは、これになります。難しい問題ですが、最近では、定式化や問題の規模次第で解けるようになってきました。
「混合整数最適化問題が解けるようになってきた」これこそが、最適化のしきいが下がってきた要因といえるでしょう。数理最適化初心者にとって、1 つの目標が、簡単な混合整数最適化問題の定式化することになるでしょう。
ただし、実務で、混合整数最適化問題を扱うのは難しく、いろいろ工夫が必要になることもあります。
非線形最適化問題
非線形最適化は、さらに難しい問題です。しかし、小規模であれば、現状でも解けるようになってきました。また、非線形最適化の中でも非線形凸最適化は、大規模なものでも扱えますが、ここでは省略します。
この3 種類の例は後ほど見てみます。
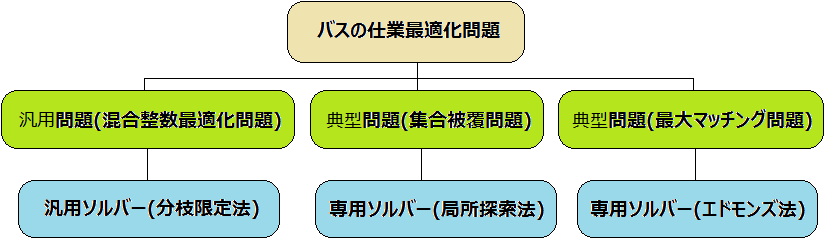
典型問題と汎用問題の関係
全ての数理最適化問題は、いずれかの汎用問題になります。汎用問題は、組合せ最適化問題の大分類と見ることができます。しかし、この分類はおおざっぱ過ぎます。生物の分類に例えると、脊椎動物や無脊椎動物のようなものです。
典型問題は、小分類と見ることができます。生物で言うと、は虫類やほ乳類でしょうか。典型問題の方が身近に感じることができますので、覚えやすいでしょう。
- 1 つの典型問題クラスでも、別々の汎用問題を含むことがあります。
- 定式化は生物でいうDNA のような設計図といえます。しかし、ある生物のDNA は1 つだけですが、1 つの問題を別々の問題としてとらえることができます。
- 汎用問題や典型問題へのとらえ方によって、ソルバー(すなわち解法) が変わります。
- 一般的に典型問題のソルバーの方が汎用問題のソルバーより効率がよいです。
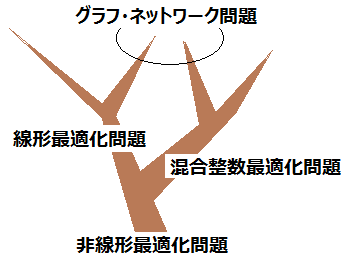
汎用問題について補足します。生物における脊椎動物と無脊椎動物は、別々のグループですが、汎用問題の分類では、基本的に包含関係になっています。すなわち、全ての問題は非線形最適化問題になっていて、その中に混合整数最適化問題があり、さらにその中に線形最適化問題があります。つまり、線形最適化問題は、混合整数最適化問題でもあり、非線形最適化問題でもあります。また、混合整数最適化問題は、非線形最適化問題でもあります。このことは、ソルバーを適用する際にもいえます。すなわち、非線形最適化ソルバーは、非線形最適化問題、混合整数最適化問題、線形最適化問題を全て扱えます。混合整数最適化ソルバーは、一般の非線形最適化問題は扱えず、混合整数最適化問題、線形最適化問題を扱えます。線形最適化ソルバーは、線形最適化問題のみ扱えます。習慣的に、混合整数最適化ソルバーと線形最適化ソルバーは、1 つのソルバーになっていることがよくあります。
非線形最適化ソルバーは、制約を考慮できるものとできないものがありますが、実務者にとっては、制約を考慮できるソルバーだけ気にしていれば十分と思われるので、ここでは制約を考慮できることを前提にしています。
ソルバーは、より小さい領域に対する方が性能がよくなります。線形最適化問題は、線形最適化ソルバーを利用する方が、早く最適解が得られます。線形最適化問題に対し、非線形最適化ソルバーを用いると、「初期解を指定する必要がある」「計算時間が膨大にかかる」などのデメリットがあります。
最適化の研究者の間では、はるかに細かい分類がありますが、多くの実務者にとっては「非線形最適化」「混合整数最適化」「線形最適化」の3 種類で十分でしょう。
混合整数最適化問題は、混合整数線形最適化問題ともよびます。
研究者は、線形最適化をLP(Linear Programing)、混合整数最適化をMIP もしくはMILP(Mixed Integer Linear Programing)、非線形最適化をNLP(Non Linear Programing) とよびます。Programing は、もともと「計画」と訳されていましたが、最近では最適化とよぶようになってきましたので、ここでも最適化で統一しています。最適化はOptimization なので、今後はよびかたも変わるかもしれません。
Python による典型問題の実行例
レッスン4
実際にやってみよう。
ナップサック問題
ナップサックに、いくつかの荷物を詰込みます。詰込む荷物の容量(size) の和がナップサックの容量(capacity) を超えないように、荷物の価値(weight) の和を最大にします。
from ortoolpy import knapsack
size = [21, 11, 15, 9, 34, 25, 41, 52]
weight = [22, 12, 16, 10, 35, 26, 42, 53]
capacity = 100
knapsack(size, weight, capacity)
>>>
(105, [0, 1, 3, 4, 5])
選択された荷物の価値の総和(105)と選択した荷物の順番([0, 1, 3, 4, 5])が得られます。
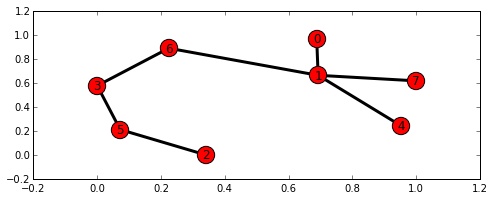
最短路問題
グラフにおいて、始点から終点までの経路の中で最も短い経路を探します。
import networkx as nx
g = nx.fast_gnp_random_graph(8, 0.26, 1)
nx.dijkstra_path(g, 0, 2)
>>>
[0, 1, 6, 3, 5, 2]
8 個の点からなるランダムなグラフを作成し、ノード0 からノード2 への最短路となるノードのリスト([0, 1, 6, 3, 5, 2]) が得られます。
その他の典型問題の実行例は、典型問題と実行方法をご覧ください。
Python による汎用問題の実行例
PuLPの使い方については、PuLPでの汎用問題の作り方を参考してください。
ナップサック問題
ナップサックに、いくつかの荷物を詰込みます。詰込む荷物の容量(size) の和がナップサックの容量(capacity) を超えないように、荷物の価値(weight) の和を最大にします。
from pulp import *
size = [21, 11, 15, 9, 34, 25, 41, 52]
weight = [22, 12, 16, 10, 35, 26, 42, 53]
capacity = 100
r = range(len(size))
m = LpProblem(sense=LpMaximize) # 数理モデル
x = [LpVariable('x%d'%i, cat=LpBinary) for i in r] # 変数
m += lpDot(weight, x) # 目的関数
m += lpDot(size, x) <= capacity # 制約
m.solve()
print((value(m.objective), [i for i in r if value(x[i]) > 0.5]))
>>>
(105.0, [0, 1, 3, 4, 5])
ナップサック問題は、汎用問題の混合整数最適化問題になります。
最短路問題
グラフにおいて、始点から終点までの経路の中で最も短い経路を探します。
from pulp import *
import networkx as nx
g = nx.fast_gnp_random_graph(8, 0.26, 1).to_directed()
source, sink = 0, 2 # 始点, 終点
r = list(enumerate(g.edges()))
m = LpProblem() # 数理モデル
x = [LpVariable('x%d'%k, lowBound=0, upBound=1) for k, (i, j) in r] # 変数(路に入るかどうか)
m += lpSum(x) # 目的関数
for nd in g.nodes():
m += lpSum(x[k] for k, (i, j) in r if i == nd) \
== lpSum(x[k] for k, (i, j) in r if j == nd) + {source:1, sink:-1}.get(nd, 0) # 制約
m.solve()
print([(i, j) for k, (i, j) in r if value(x[k]) > 0.5])
>>>
[(0, 1), (1, 6), (3, 5), (5, 2), (6, 3)]
最短路問題は、汎用問題の線形最適化問題になります。最短路問題は、ダイクストラ法という効率のよい解法があります。汎用問題として解くのは、おすすめしません。ダイクストラ法は、Python による典型問題の実行例の例(nx.dijkstra_path)で用いられています。
ポートフォリオ最適化問題
銘柄を購入する割合($x_i$)を決めます。投資に対する利益の下限(t/円)を条件として、リスク(分散($v_i$))を最小化します。ただし、各銘柄間は独立とします。
import numpy as np, scipy.optimize as so
p = [31, 86, 29, 73, 46, 39, 58] # 利益 / 円
v = [10, 60, 25, 50, 35, 30, 40] # 分散 / 円
t = 50 # 目標利益 / 円
so.fmin_slsqp(lambda x: sum(v*x*x), np.zeros(len(p)),
eqcons=[lambda x: sum(x) - 1], ieqcons=[lambda x: sum(p*x) - t])
>>>
Optimization terminated successfully. (Exit mode 0)
Current function value: 4.50899167487
Iterations: 14
Function evaluations: 136
Gradient evaluations: 14
array([ 0.26829785, 0.13279566, 0.09965076, 0.1343941 , 0.11783349,
0.11506705, 0.13196109])
ポートフォリオ最適化問題は、汎用問題の非線形最適化問題になります。
グラフ・ネットワーク
組合せ最適化問題では、グラフ・ネットワークの問題がたくさんあります。重要ですので、ここで簡単にご紹介します。
グラフとは、点と点同士を結ぶ辺で構成される構造です。現実の関係を抽象的に表現するためによく用いられます。
$G = (V, E)$ とは、「グラフ(G)が点集合(V)と辺集合(E)で構成される」ことを表します。
辺が一方通行のものを有向グラフ、そうでないものを無向グラフといいます。ある点から、別の点へ続く一連の辺を経路といいます。経路の始点と終点が繋がっているものを閉路といいます。
グラフ上の辺に何かしらを流れを考えたものをネットワークといいます。道路ネットワーク、通信ネットワークなどがあります。
ソフトのインストール
インストールが簡単にできる方法として、Anaconda を利用する方法をおすすめします。Anaconda のインストールは、サイトからインストーラをダウンロードして実行してください。
Anaconda には、Python 本体と科学技術計算用の多くのパッケージが含まれています。Anaconda 以外に必要なソフトは、数理最適化のモデラーであるPuLP と典型問題用ライブラリになります。
- PuLP のインストールは「pip install pulp」とします。
- 典型問題用ライブラリのインストールは「pip install ortoolpy」とします。
PuLPでの汎用問題の作り方
- ライブラリのインポート
- from pulp import *
- 数理モデルの作成
- 最小化問題のとき: m = LpPrblem()
- 最大化問題のとき: m = LpProblem(sense=LpMaximize)
- 変数の作成
- 連続変数: x = LpVariable(変数名, lowBound=0)
- 0-1変数: x = LpVariable(変数名, cat=LpBinary)
- 連続変数のリスト: x = [LpVariable(i番目の変数名, lowBound=0) for i in range(n)]
- 変数名は、必ず異なるようにします
- 目的関数の設定
- m += 式
- 制約条件の追加
- m += 式 == 式
- m += 式 <= 式
- m += 式 >= 式
- 式の例
- 2 * x + 3 * y - 5
- 和: lpSum(変数のリスト)
- 内積: lpDot(係数のリスト, 変数のリスト)
- ソルバーの実行
- m.solve()
- 変数や式や目的関数の値
- value(変数)、value(式)、value(m.objective)
参考
注意すべきポイント
実務で最適化を使う上で注意すべきポイントがいくつかあります。現在の最適化技術では、現実の課題を完全にモデル化することはできません。重要度の低い部分を切り捨てて、モデルをシンプルにしないと解くことができません。
従って、最適化の結果は、そのままでは現実には使えないことも多くなります。その場合、どういう問題が生じるのかを確認するために、検証をすることが重要になります。問題をいち早く見つけるために結果の見せ方も重要です。
理解を深めるために
さらなる勉強のためのキーワードをあげておきます。
- 計算量、オーダー記法、クラスP、クラスNP
- オペレーションズ・リサーチ、モデリング、メタヒューリスティック、双対性、緩和問題、人工知能、機械学習、ゲーム理論
- 関連学会
- 最適化の話題や解説
余談
生物では、リンネによる二命名法(例えば人類はホモ・サピエンス) が一般的ですが、最適化でも、汎用問題・典型問題のとらえ方はこれに似ているかもしれません。
汎用問題か典型問題かのどちらとしてとらえるかにより、ソルバーが変わりますが、ユーザーが判断して選択する必要があります。将来は、自動で判別できるようになるかもしれません。すなわち、汎用問題としてソルバーに与えると、解析していずれかの典型問題であることがわかれば、自動的により効率的な解法を用いるようになるかもしれません。
東ロボくんをご存じでしょうか?
国立情報学研究所が中心となって、「ロボットは東大に入れるか」をテーマにした研究プロジェクトです。
実は、典型問題による最適化アプローチは、東ロボくんのアプローチと似ているところがあります。それは、千差万別の問題を類型問題としてとらえて解くというところです。
この試みを見ていると、日本語で問題を記述するだけで、自動で最適化して解けるようになる日が、いずれ来ると思われます。
しかし、それまでは自分で考えて、手を動かす必要があるでしょう。また、そうすることによって、徐々に、より複雑な問題への対処法を身につけることができると思います。