線形緩和問題とは
組合せ最適化における混合整数最適化問題の整数制約を取り除いてできる問題を(混合整数最適化問題の)線形緩和問題といい、線形最適化問題になります。
そもそも緩和問題1とは
元の問題の制約条件の一部または全部を削除してできる新たな問題を、元の問題の緩和問題とよびます。
特徴
制約条件がなくなっているので、実行可能領域は広がります。従って、下記の特徴があります。
- 最大化問題の場合、緩和問題の最適解は元の問題の上界になります(最小化なら下界)。
- 緩和問題の最適解が元の問題で実行可能ならば、元の問題の最適解になります。
- 基本的に元の問題より解きやすくなります。
線形緩和とは
緩和の一種で、整数制約を削除することです。
(参考までに)ラグランジュ緩和とは
- 元の非線形最適化問題の制約条件を削除して、制約条件を違反する量をペナルティとして目的関数に加えてできる新たな問題を、元の問題のラグランジュ緩和問題とよびます。
- 適切なペナルティの重み(ラグランジュ乗数)を決めてやると、ラグランジュ緩和問題の最適解は元の問題の最適解になります。
- ラグランジュ緩和問題は無制約になり、利用可能なアルゴリズムが増えて解きやすくなります。
- ただし、混合整数最適化問題のラグランジュ緩和問題を考えてもあまり意味はありませんので、ここでは紹介のみとします。
なぜ緩和するのか
例えば線形緩和は、分枝限定法で利用されます。
他にも、近似解を得たり、感度分析したり、双対定理の証明などで使われます。
なお、曲線の関数を折れ線で表すのは、区分線形近似とよばれ、緩和ではありません。
例題(ナップサック問題)による確認
図示しやすいように3変数の以下の混合整数最適化問題2であるナップサック問題を考えましょう。
混合整数最適化問題の定式化
| 最大化 | $7x+8y+9z$ |
|---|---|
| 制約条件 | $6x+7y+8z \le 14$ |
| $x,y,z \in \{0,1\}$ |
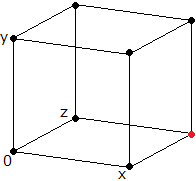
混合整数最適化問題の解空間と最適解(赤い点)の図示
混合整数最適化問題のPythonによる求解
python
from pulp import *
m = LpProblem(sense=LpMaximize) # 数理モデル
x,y,z = [LpVariable(c,cat=LpBinary) for c in 'xyz'] # 変数
m += lpDot([7,8,9], [x,y,z]) # 目的関数
m += lpDot([6,7,8], [x,y,z]) <= 14 # 制約条件
m.solve() # 求解
print([value(v) for v in [x,y,z]]) # 出力
>>>
[1.0, 0.0, 1.0]
線形緩和問題の定式化
| 最大化 | $7x+8y+9z$ |
|---|---|
| 制約条件 | $6x+7y+8z \le 14$ |
| $x,y,z \ge 0, ~~\le 1$ |
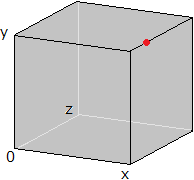
線形緩和問題の解空間と最適解(赤い点)の図示
線形緩和問題のPythonによる求解
python
from pulp import *
m = LpProblem(sense=LpMaximize) # 数理モデル
x,y,z = [LpVariable(c,lowBound=0,upBound=1) for c in 'xyz'] # 変数
m += lpDot([7,8,9], [x,y,z]) # 目的関数
m += lpDot([6,7,8], [x,y,z]) <= 14 # 制約条件
m.solve() # 求解
print([value(v) for v in [x,y,z]]) # 出力
>>>
[1.0, 1.0, 0.125]
以上