図で見る分枝限定法

分枝限定法とは

各種最適化問題の最適解を求める汎用アルゴリズムである。分枝操作と限定操作から構成される。全ての解候補を体系的に列挙するもので、最適化された量の上限と下限の概算を使って、最適でない候補は「ひとまとめに」捨てられる。 ――― wikipediaより

組合せ最適化の中の混合整数最適化問題を解くソルバーにおいて、よく使われる手法です。
全ての可能性を調べるので、厳密な最適解を求められます。しかし、下記の限定操作により、効率よく計算することができます¹。
以下では、ナップサック問題を例に説明するので、最大化問題とします。

• 暫定解：現在までで最良となる解。以下の例では、最初に貪欲法で求めています。
• 分枝操作：問題を分割する操作。以下の例では、1個の(0または1をとる)バイナリ変数の値を固定して2つの問題に分けています。
• 限定操作：分割された子問題に対し以下を考えます。
  • 上界を求める：求めた上界が暫定解値以下であれば、子問題を解いても、暫定解を更新できませんので、その子問題に対しては分枝操作はしません。
  • 下界を求める：求めた下界が暫定界値以上であれば、暫定界を下界で更新します。以下の例では、実行可能解を下界にしています。

上界を求める方法としては、線形緩和がよく使われます。

例題(ナップサック問題)で確認

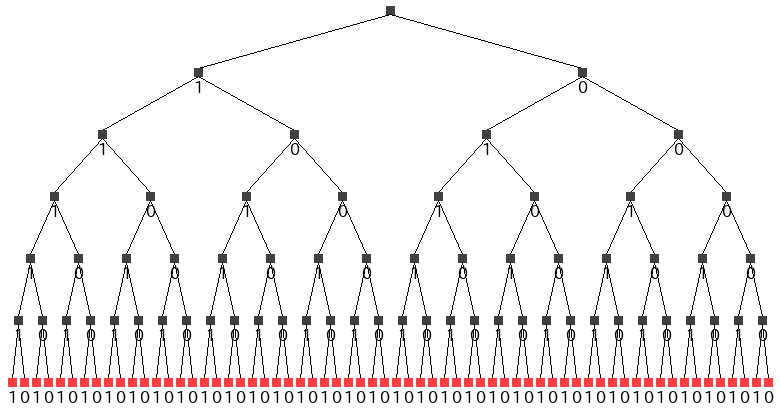
荷物が6個のナップサック問題を考えて見ましょう。全て列挙すると、$2^6 = 64$通りを調べることになります。Pythonで図示してみましょう。

python

from PIL import Image, ImageDraw, ImageFont
fn = ImageFont.truetype(r'C:\Windows\Fonts\ipaexg.ttf', 16)
def func1(dr, fn, ini, pos, x, pr, lab):
    y = pos*62+10
    if pr:
        dr.line((*pr,x,y-4),'black')
    dr.rectangle((x-4,y-4,x+4,y+4),f'#{"ff"if pos==6 else "40"}4040')
    dr.text((x-4,y+6), f'{lab}', 'black', fn)
    if pos < len(ini):
        w = 3*64>>pos
        ini[pos] = 1
        func1(dr, fn, ini, pos+1, x-w, (x,y+4), '1')
        ini[pos] = 0
        func1(dr, fn, ini, pos+1, x+w, (x,y+4), '0')
        ini[pos] = -1
im = Image.new('RGB', (780,408), (255,255,255))
dr = ImageDraw.Draw(im)
func1(dr, fn, [-1]*6, 0, 390, None, ' ')
im

• 四角が1つの問題を表し、一番上の四角が元の問題を表しています。
• 四角の下から出ている2本の線は、分枝操作で2つの子問題に分けていることを表しています。
• 元の問題の左下の四角は、最初の荷物を「必ず選ぶ」(=1)ように固定した問題を、右下の問題は「必ず選ばない」(=0)ように固定した問題を表しています。
• 最下段の赤い四角は、全ての荷物が0か1に固定された問題を表しており、$2^6 = 64$個あります。

上界を求める

線形緩和して、上界を求めるknapsackを定義します。iniは、固定されている状態を表す配列です(負ならば非固定)。
また、実行可能解がない場合は、0を返します。

python

from pulp import *
def knapsack(ini):
    m = LpProblem(sense=LpMaximize) # 数理モデル
    x = [LpVariable(f'x{i}',lowBound=0,upBound=1) for i in range(6)] # 変数
    m += lpDot([22,24,26,28,29,30], x) # 目的関数
    m += lpDot([10,11,12,13,14,15], x) <= 48 # 制約条件
    for i,v in zip(ini,x):
        if i >= 0:
            m += v == i
    m.solve() # 求解
    return value(m.objective) if m.status==1 else 0

限定操作を組み込んでツリーを描く

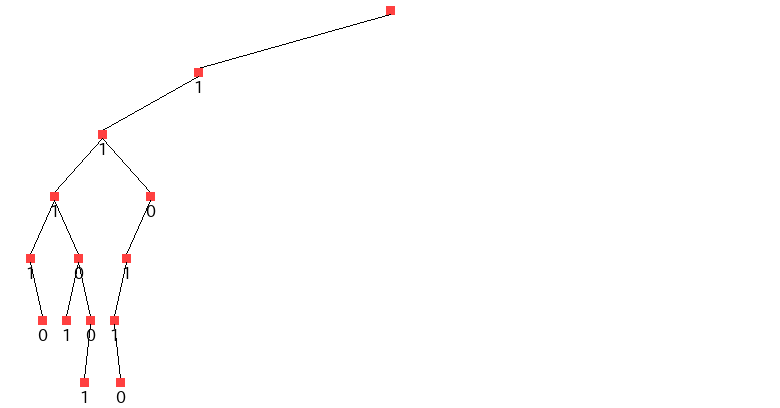
上界と暫定解を比較し、最適解が更新できないことがわかれば、描画しないようにします。
なお、暫定解の初期値は、貪欲法で 102 とわかっているものとします。

python

def func2(dr, fn, ini, pos, x, pr, lab, zantei):
    r = knapsack(ini)
    if r < zantei[0]-1e-4:
        return
    y = pos*62+10
    if pr:
        dr.line((*pr,x,y-4),'black')
    dr.rectangle((x-4,y-4,x+4,y+4),f'#ff4040')
    dr.text((x-4,y+6), f'{lab}', 'black', fn)
    if pos < len(ini):
        w = 3*64>>pos
        ini[pos] = 1
        func2(dr, fn, ini, pos+1, x-w, (x,y+4), '1', zantei)
        ini[pos] = 0
        func2(dr, fn, ini, pos+1, x+w, (x,y+4), '0', zantei)
        ini[pos] = -1
    else:
        if zantei[0] < r:
            zantei[0] = r
im = Image.new('RGB', (780,408), (255,255,255))
dr = ImageDraw.Draw(im)
func2(dr, fn, [-1]*6, 0, 390, None, ' ', [102])
im

大部分の子問題を解かなくてもよいことがわかります。なお、厳密な最適解は、[1,1,0,1,1,0](最下段右側)の時の 103 であり、この時点で暫定解は 103 になります。

ツリーの右側(最初の荷物を0に固定した問題)は、全て消えています。確認してみましょう。

python

print(f'{knapsack([0,-1,-1,-1,-1,-1]):.2f}')
>>>
102.86

最初の荷物を0で固定にして、残りを-1で非固定にして求めます。
上界が 102.86 なので暫定解 103 より悪いため、限定操作で、この子問題で探索は終わりになります。

以上

1. うまく分枝操作をすることによって、効率がよくなります。 ↩