はじめに
OR-Tools (Operations Research Tools)でパズルを自動生成する話の第3弾です。
今回は、スターバトルの問題自動生成を行います。
スターバトルとは
ルールについては こちら を見て下さい。
要約すると次の3点です。
- 盤面の白マスに、星を入れる。
- 全ての縦列、横列、太線で区切られた領域には、星が指定された個数ずつ入る。
- 星同士が縦横斜めに隣り合ってはならない。
ソルバを作る
これまでの他のパズルのときと同様、まずはソルバを作ります。割とシンプルに作ることができました。
OR-Toolsの CpModel でブール型の二次元配列 cells[][] を作ります。指定された星の数を m として、各列・行・領域に関する条件を、sum([cells[i][j] for j in range(n)]) == m のように表します。
もう一つのルール、星同士が縦横斜めに隣り合ってはならないルールについても制約を付けます。盤面上の全ての隣り合うセルの対について、たかだか1個の星しか入らないという制約に読み替えます。cells[i][j] + cells[i+1][j] <= 1 のように表します。
以上の制約を用いたソルバを以下に示します。別解ありの場合は例外を投げるようにしています。
from ortools.sat.python import cp_model
class Solver(cp_model.CpSolverSolutionCallback):
def __init__(self, cells):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__cells = cells
self.__solutions = []
def OnSolutionCallback(self):
n = len(self.__cells)
solution = [[self.Value(self.__cells[row][col]) for col in range(n)] for row in range(n)]
if len(self.__solutions) != 0:
raise TooManySolutionError('')
self.__solutions.append(solution)
def Solutions(self):
return self.__solutions
def solve(board, m):
n = len(board)
model = cp_model.CpModel()
cells = [[model.NewBoolVar(f'cell_{i}_{j}') for i in range(n)] for j in range(n)]
# 各行・列でマークはm個だけ
for i in range(n):
model.Add(sum([cells[i][j] for j in range(n)]) == m)
model.Add(sum([cells[j][i] for j in range(n)]) == m)
# 区切られた各ブロックでマークはm個だけ
arrays = {}
for i in range(n):
for j in range(n):
id = board[i][j]
if id not in arrays: arrays[id] = []
arrays[id].append(cells[i][j])
for array in arrays.values():
model.Add(sum(array) == m)
# 隣接制約の追加
for i in range(n):
for j in range(n):
if i > 0: # 上のセル
model.Add(cells[i][j] + cells[i-1][j] <= 1)
if i < n - 1: # 下のセル
model.Add(cells[i][j] + cells[i+1][j] <= 1)
if j > 0: # 左のセル
model.Add(cells[i][j] + cells[i][j-1] <= 1)
if j < n - 1: # 右のセル
model.Add(cells[i][j] + cells[i][j+1] <= 1)
if i > 0 and j > 0: # 左上のセル
model.Add(cells[i][j] + cells[i-1][j-1] <= 1)
if i > 0 and j < n - 1: # 右上のセル
model.Add(cells[i][j] + cells[i-1][j+1] <= 1)
if i < n - 1 and j > 0: # 左下のセル
model.Add(cells[i][j] + cells[i+1][j-1] <= 1)
if i < n - 1 and j < n - 1: # 右下のセル
model.Add(cells[i][j] + cells[i+1][j+1] <= 1)
solver = cp_model.CpSolver()
solution_printer = Solver(cells)
solver.SearchForAllSolutions(model, solution_printer)
return solution_printer.Solutions()
if __name__ == '__main__':
board = [
[1, 1, 1, 2, 3],
[1, 1, 1, 2, 3],
[4, 2, 2, 2, 3],
[4, 4, 4, 3, 3],
[4, 4, 4, 5, 5],
]
solutions = solve(board, 1)
for row in solutions[0]: print(row)
問題の自動生成
次に問題の自動生成です。ヒントをランダムに生成するアプローチを試みます。太線で区切られた領域をランダムに生成して、ソルバに解かせ、唯一解が得られれば終了。得られなければ再トライを繰り返します。
生成をどう行うかは頭を使うところです。ゼロで初期化した二次元配列の盤面からランダムに開始点を選び、そこから上下左右に領域をランダムに広げていくという方法をとりました。
こんな感じのコードです。実はこのコードは不十分で、領域が未割当の領域が残る可能性があるのですが、後述の通り今回はこれで良しとしました。
def generate_random_connected_regions(n, region_count):
grid = [[-1 for _ in range(n)] for _ in range(n)]
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)] # 右, 下, 左, 上
def dfs(x, y, region_id):
stack = [(x, y)]
visited = set(stack)
region_size = 0
while stack and region_size < n*n // region_count:
cx, cy = stack.pop()
grid[cx][cy] = region_id
region_size += 1
random.shuffle(directions)
for dx, dy in directions:
nx, ny = cx + dx, cy + dy
if is_valid_move(nx, ny, n, grid, visited):
stack.append((nx, ny))
visited.add((nx, ny))
# 領域をランダムに開始点から拡張
for region_id in range(region_count):
while True:
start_x, start_y = random.randint(0, n-1), random.randint(0, n-1)
if grid[start_x][start_y] == -1:
dfs(start_x, start_y, region_id)
break
# 割り当てられていないセルがある場合、上下左右の領域に割り当てる
for i in range(n):
for j in range(n):
if grid[i][j] == -1:
for dx, dy in directions:
ni, nj = i + dx, j + dy
if 0 <= ni < n and 0 <= nj < n and grid[ni][nj] != -1:
grid[i][j] = grid[ni][nj]
break
return grid
以上の道具を使った問題生成のコードです。未割当の領域が残ってないかどうかをチェックして、もしあれば破棄してやり直しとしています。また星の個数ちょうどの広さの領域がある場合も破棄しています(問題としてつまらないため)。
def provide(n, m):
while True:
board = generate_random_connected_regions(n, n)
ok = True
# 未割当の領域が残っていればやり直し
counts = {i: 0 for i in range(n)}
for i in range(n):
for j in range(n):
if board[i][j] == -1:
ok = False
break
counts[board[i][j]] += 1
for c in counts.values():
if c <= m: ok = False
if not ok:
continue
try:
solutions = solve(board, m)
except TooManySolutionError as e:
continue
if len(solutions) != 1:
continue
for row in board: print(row)
break
if __name__ == '__main__':
provide(7, 1)
出力例
こんな結果が出ました。



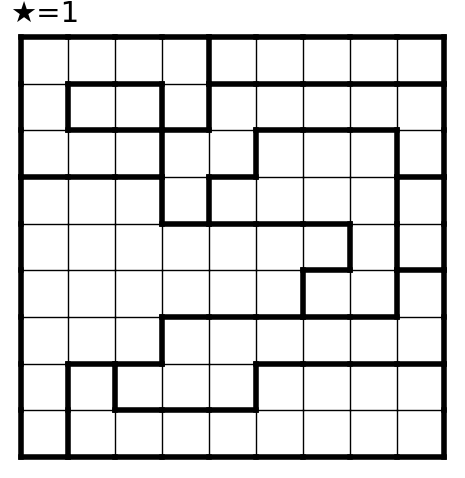

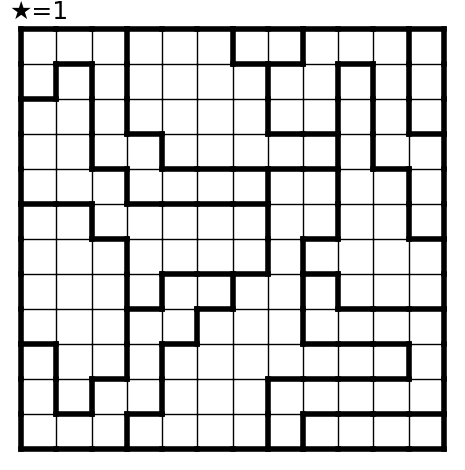


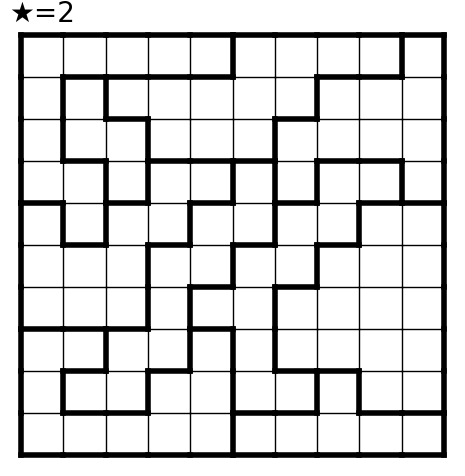
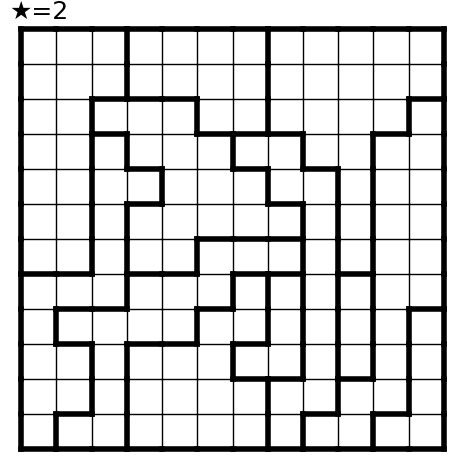
所感
ランダム生成したパズルが実際に唯一解をもつ確率はかなり小さかったです。盤面のサイズや星の数にもよりますが、★=1の場合、7×7で1%、12×12で0.01%ぐらい。さすがに大サイズだと低かったです。ただ今回の場合は、ソルバが非常に高速に動作してくれるので、このぐらいの低確率のガチャでも、PCをぶん回せば、まあ待てる時間で当たりを引いてくれました。このパズルは比較的すくない制約でルールを表現できるため、高速な解の導出ができたものと思います。特に今回は、完全にランダムに盤面を生成するというかなり乱暴なアプローチだったわけですが、それでも繰り返しの試行錯誤の力を借りて、現実的な待ち時間でちゃんと生成できるようになったのは面白いと思います。
実際に手で解いてみました。★=1の場合は割とさくさく解き進められますが、★=2の場合は手も足も出なかったです。手作りパズルだと、いわゆる「とっかかり」を出題者が意図して用意することが多いですが、そのような忖度は当然ながらありませんでした。
おわりに
OR-Toolsを使って、スターバトルの問題の自動生成を行いました。

