はじめに
CNNを使った機械学習では、モデルの選択だけでなく、そのモデルのパラメータ(重み)をどうやって変えていくかも重要です。この記事では、画像セグメンテーションをメインにして、学習を最適化するために必要な損失関数とオプティマイザについて解説していきます。またMRI画像をつかったセマンティックセグメンテーションで比較もしてみました。
すでに同様の記事はネット上に山ほどありますが、この記事は勉強兼自分なりにまとめたらどうなるだろうかと考えた結果のものなので、大目にみてくださいm(_ _)m
記事中では機械学習モジュールとしてtensorflow, keras(tf.keras)を用います。動作環境は(記事公開時点で)v2.4.1です。
1. 機械学習はどうやって学習されるか
ここではそれぞれの細かいことは説明せず、ざっくりとだけ説明します。
画像で学習過程を表すと、次のようになります。
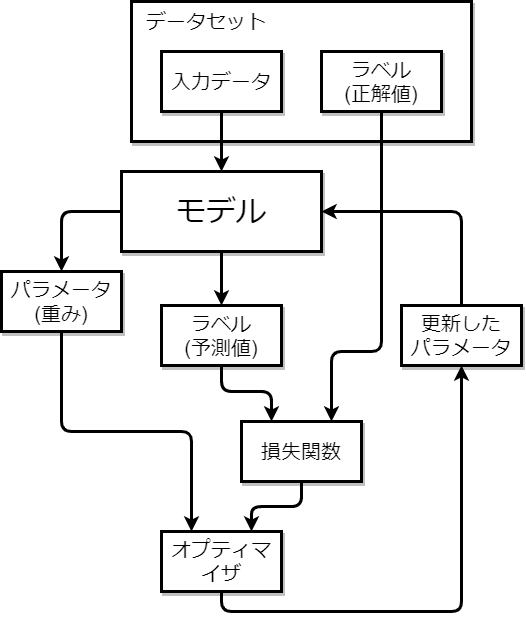
まずはじめに、学習用の入力データ(画像)をモデルにインプットします。データはモデルに通され、最終的に何らかの予測値がモデルから出力されます。2値分類でいえば[0,1]の確率、画像セグメンテーションではマスク画像になります。
次に、入力データの正解値、そしてモデルから出力された予測値をそれぞれ損失関数に入力します。ここで得られた値は、モデルのパラメータとともにオプティマイザに引き渡され、そしてその出力値はモデルの新しいパラメータとしてモデルに代入されます。これが1回の学習となり、再びデータのインプットからスタートします。
この繰り返しによってモデルの重みは変化して学習が行われます。学習はいつ学習は終わるの?、というと、理想的には損失関数が0になったときですが、(0になることなんてそうそう無いので)実際はエポック数やコールバックを使ってある程度の学習回数で止めになります。
2. 損失関数(Loss)
損失関数は予測値が真の値に対してどれだけ近いかを表す関数、あるいは正解と予測との尺度を意味します。
ニューラルネットワークには多くの重みやバイアスが存在し、モデルに入力されたデータはその重みによって最終的にデータから予測される値、すなわち予測値が出力されます。
例えば、1つのニューロンだけのネットワークに何らかの入力値$x$があるとすると、重みを$w$、バイアスを$b$とすれば出力$\hat{y}=wx+b$と書けます。この$\hat{y}$が予測値となり、正解値$y$とどれほど近いかを損失関数を用いて評価します。
損失関数の中で有名かつ説明しやすい例として、平均2乗誤差(Mean Square Error : MSE) を例に挙げてみます。$N$個のデータがあるとして、正解値を$y$、予測値を$\hat{y}$とします。その場合、MSEは次のように表現できます、
L_{\text{MAE}}=\frac{1}{N}\sum_{i=1}^{N}(y-\hat{y})^2
MSEは正解値を予測値で引いたものを2乗し、その総和の平均をとります。予測値が正解値に近ければ損失は小さく、遠ければ損失は大きくなるのはすぐにわかりますね。
Cross Entropy (CE)
クロスエントロピーは多くのタスクで頻繁に使われている損失関数です。tensorflowに限らず、PyTorchの公式等のチュートリアルとかでこの名前を見たことがある人は多いと思います。具体的なことは省略しますが、簡単にいえば「正解と予測がどれだけ離れているか」という所でしょうか。
クラス数が2つの場合(犬と猫の画像しかないデータセットの分類など)に使うクロスエントロピーを「2値クロスエントロピー(Binary Cross Entropy : BCE)」、2つ以上の場合(犬、猫、鳥などの複数の種類が含まれたデータセットの分類など)を「多クラスエントロピー(Categorical Cross Entropy : CCE)」と呼びます。
tensorflowにおいては次の通りです
import tensorflow as tf
# 2値クロスエントロピー
bce = tf.keras.losses.BinaryCrossentropy()
# 多クラスクロスエントロピー
cce = tf.keras.losses.CategoricalCrossentropy()
モデルをコンパイルする場合は、strで書き込んでもokです。
# BCEの場合
model.compile(optimizer='adam',
loss='binary_crossentropy', # ココ
metrics=['accuracy'])
# CCEの場合
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
BCEやCCEはデータのクラス分布がある程度均衡なデータセット(例えば犬、猫との画像がほぼ1:1で含まれているようなデータセット)でよく使われています。画像のセグメンテーションで考えれば、黒と白がちょうど半々みたいなデータで使われる感じでしょうか。
もちろん不均衡な場合でのエントロピーというのも存在します。偏りがある場合は重み付けされたCEである「Weighted Cross Entropy」、かなり不均衡(1:99みたいな)な場合は「Focal Cross Entropy」というものがありますが、ここでは紹介は省かせていただきます。
Dice Loss
Dice損失は2つの要素の類似度の評価するために使われているDice係数(F値)を損失として用いたものです1。ざっくり言ってしまえば、「正解値に対して予測値はちゃんと検出できているか?」を見ます。
L_{\text{DICE}}=1-\text{DC}=1-\frac{2\sum_{i=1}^{N}y_i\hat{y}_i+1}{\sum_{i=1}^{N}(y_i+\hat{y}_i)+1}
Nは1データにおける体積(ボクセル)です。(256x256x3)のRGB画像はN=256x256x3=196608です。また分子分母に1がありますが、これはゼロ除算対策になります。
tensorflowにおいては、残念ながら標準実装はありません(あってもいいと思うんですが)。自前で定義する場合は、次のようになります。
def dice_loss(y_true: tf.Tensor, y_pred: tf.Tensor) -> tf.Tensor:
smooth = 1. # ゼロ除算回避のための定数
y_true_flat = tf.reshape(y_true, [-1]) # 1次元に変換
y_pred_flat = tf.reshape(y_pred, [-1]) # 同様
tp = tf.reduce_sum(y_true_flat * y_pred_flat) # True Positive
nominator = 2 * tp + smooth # 分子
denominator = tf.reduce_sum(y_true_flat) + tf.reduce_sum(y_pred_flat) + smooth # 分母
score = nominator / denominator
return 1. - score
Dice損失はよくクロスエントロピーと組み合わせて使われています2。BCEとDiceの組み合わせはBCE Dice Loss、CCEとDiceの組み合わせはCCE Dice lossとかで呼ばれています。
def bce_dice_loss(y_true: tf.Tensor, y_pred: tf.Tensor) -> tf.Tensor:
return 0.5 *(bce(y_true, y_pred) + dice_loss(y_true, y_pred))
def cce_dice_loss(y_true: tf.Tensor, y_pred: tf.Tensor) -> tf.Tensor:
return 0.5* (cce(y_true, y_pred) + dice_loss(y_true, y_pred))
Tversky Loss
TverskyLossはDice係数の疑陽性(FP)と偽陰性(FN)に重みがつられたものになります3。重みを$\alpha$とおけば損失は次のようになります。
L_\text{T}=1-\text{TI}=1-\frac{\sum_{i=1}^{N}(y_i\hat{y}_i)+1}{\sum_{i=1}^{N}(y_i\hat{y}_i)+\alpha\sum_{i=1}^{N}\{(1-y_i)\hat{y}_i\}+(1-\alpha)\sum_{i=1}^{N}\{y_i(1-\hat{y}_i)\}+1}
ちなみに$\alpha=1/2$とおくとDice損失になります。元の論文では$\alpha=0.3$がベストのようです。
こちらもtensorflowの公式実装はありません。自前で実装する場合は次のようになります。
def tversky_loss(y_true: tf.Tensor, y_pred: tf.Tensor) -> tf.Tensor:
alpha = 0.3 # FP、FNの重み
smooth = 1. # ゼロ除算回避のための定数
y_true_flat = tf.reshape(y_true, [-1]) # 1次元に変換
y_pred_flat = tf.reshape(y_pred, [-1]) # 同様
tp = tf.reduce_sum(y_true_flat * y_pred_flat) # True Positive
fp = tf.reduce_sum((1 - y_true_flat) * y_pred_flat) # False Positive
fn = tf.reduce_sum(y_true_flat * (1 - y_pred_flat)) # False Negative
score = (tp + smooth)/(tp + alpha * fp + (1-alpha) * fn + smooth) # Tversky
return 1. - score
派生として、不均衡な場合の「Focal Tversky Loss」というのもあります4。これは次の式で表されます。
\text{FTL} = L_\text{T}^\frac{1}{\gamma}
ここで$\gamma$は$[1,3]$の値です。元の論文では$4/3\simeq1.33$が使われています。実装すると次のようになります。
def focal_tversky_loss(y_true: tf.Tensor, y_pred: tf.Tensor) -> tf.Tensor:
gamma = 0.75 # 1/(4/3)=3/4=0.75
tversky = tversky_loss(y_true, y_pred)
return tf.pow(tversky, gamma)
どの損失関数を用いるべきか
損失関数のバリエーションは非常に多いです。セグメンテーションで使われている損失はこんなにあります
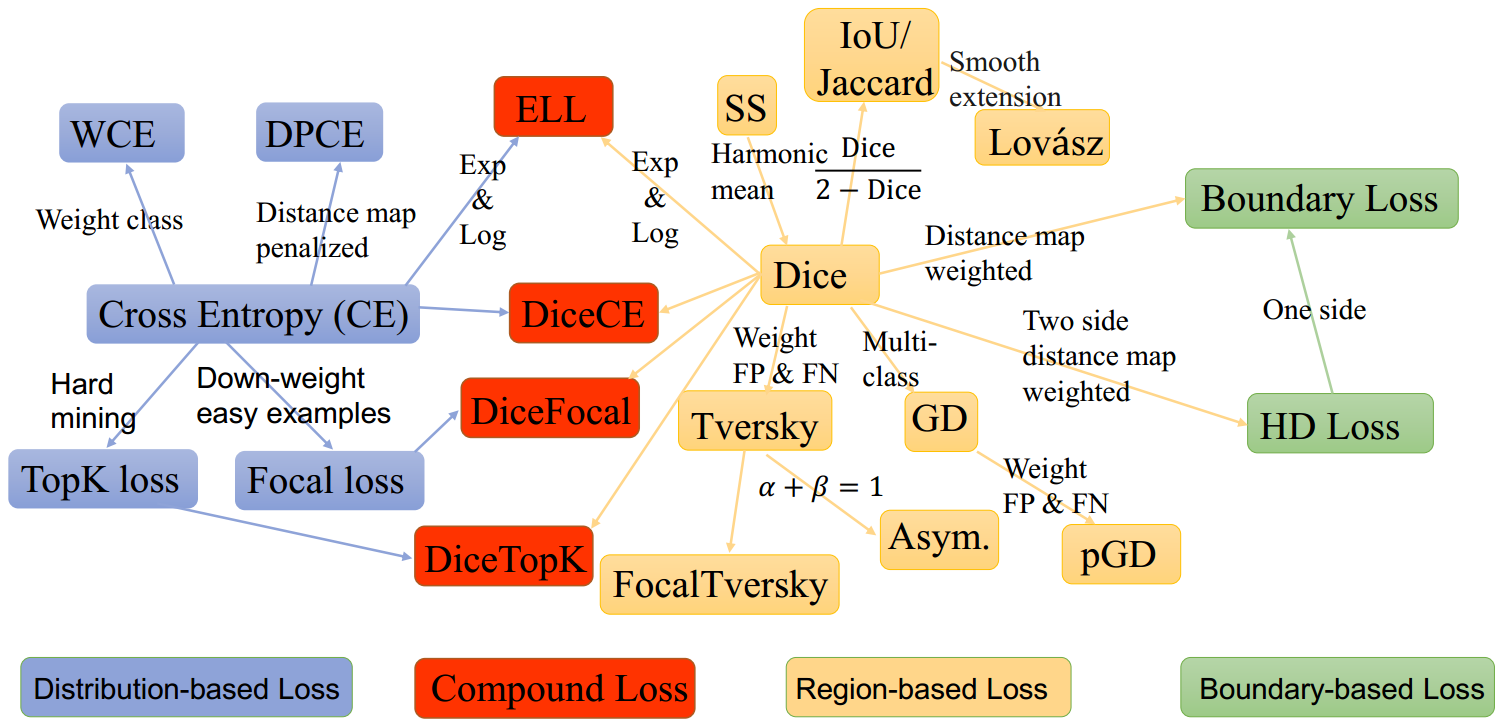
画像 : JunMa11/SegLoss
それぞれの損失関数には長所短所があります。そのため、すべてにおいて万能な損失関数というのは存在しませんし、おそらく今後は出てこないんじゃないかなと思ってます。
簡単なデータセットだとほとんどはクロスエントロピーで十分な結果が得られますが、医療画像などを扱う場合はそんな簡単にはいきません。医療画像の場合、検出したい部分が小さいために、付加されたマスク領域も小さくなるという場合が多いからです。そこで出てくるのが重み付加された損失(Weighted CE, Tversky)や、偏りが激しい場合のFocal系(Focal Loss, Focal Tversky)です。
ただ結局のところ物は試しなので、解析したいデータセットを見てまずはCEやDiceでやってみて、損失があまり上がらなかったら重み付きのものを試すといいかもしれません。それでもだめだったら、次から述べるオプティマイザについても考慮してみるといいかもしれません。
3. オプティマイザ (Optimizer)
損失関数は正解値と予測値がどれだけ近いかを示すための関数でした。求めた損失をどうやってモデルの重みに反映させるかで登場するのがオプティマイザです。
オプティマイザも損失関数と同じくその種類は多くあります。ただ、それらの種類はほぼすべて最急降下法(Gradient Descent) の改良版になります5。
最急降下法というのは、「求まった損失を微分し、その傾き(勾配)から損失が最小になるように次のモデルの重みを決定する」という手法です。図で表すと、次のようになります。
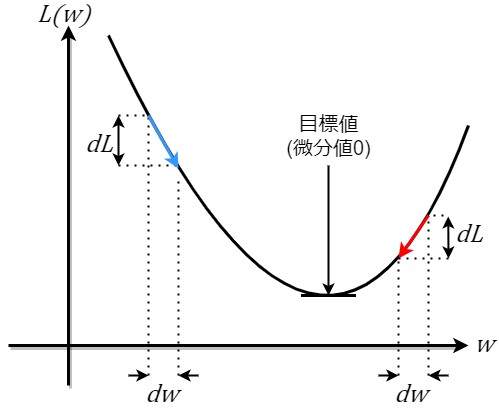
まずはじめに、正解値$y$と予測値$\hat{y}$から損失を求めます。$\hat{y}$には損失関数の項でも説明したように重みがかかっているので、損失は$L(w)$と書けます
(今回は重みが1個なので、損失は上のような曲線で説明ができますが、実際は数100万、数億の重みがあるので、今回は簡単のためだと思ってください)。
そしたらこの損失の一階微分を求めます。微分は「変化の具合」を見るものなので、損失を微分すれば真の値と予測値がどのように変化したかがわかります。

上の青線傾きは負であることがわかりました。学習では微分したときの傾きが0(損失が最小)になるようにしたいです。そのため、損失のパラメータである重みをこの微分結果を用いて更新します。$t$回目の学習では、その式は次で表されます。
w_{t+1}=w_t-\eta\frac{dL}{dw}
ここで$\eta$は区間$[0,1]$の学習率です。学習率は「微分結果を重みにどれだけ反映させるか」を示す値です。最急降下法ではこの式を用いてモデルの重みを更新していきます。実際のところ、重みは1つだけでなく大量にあるので、上記の式は勾配$\nabla_w$をもちいて次のようになります。
w_{t+1}=w_t-\eta\nabla_wL(w)
Stochastic Gradient Descent (SGD)
最急降下法には欠点もあります。その欠点というのは、最小値でない極小値に収束してしまう可能性があるということです。
例えば下のような損失関数があるとします。
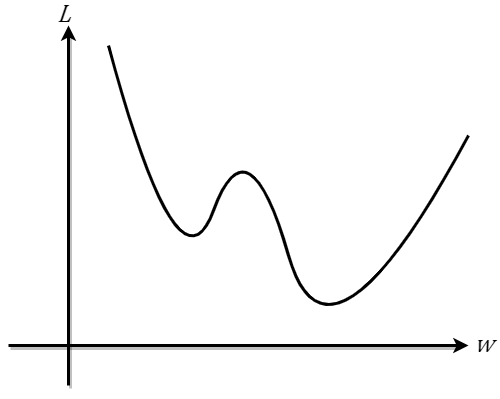
上は極小値が2つあるような曲線です。目標はもちろん最小値ですが、初期値の重みの設定が悪いと、最小値でない別の極小値に収束してしまいます。もし収束してしまうと、微分が0になりそれ以上学習されなくなってしまいます。これは局所解(または勾配消失)と呼ばれていて、これにハマってしまうと精度の悪いモデルができてしまいます。
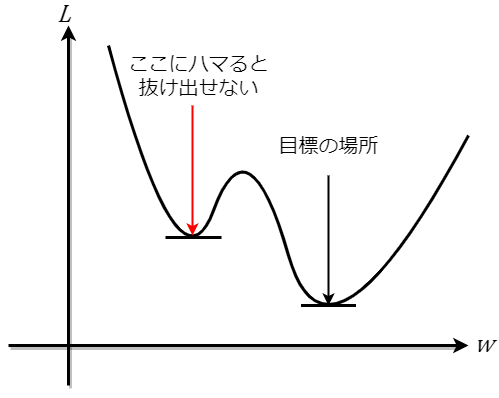
この局所解が発生する問題を解決する手段として定義されたのが、確率的最急降下法(Stochastic Gradient Descent : SGD) です。
最急降下法では重みの更新のためにすべての重みを用いましたが、SGDではランダムにピックアップした1つのパラメータを用います。パラメータを1つだけにすることで、別の極小値に行ってしまっても、ランダム性によってそこから脱出することが可能になるのです。ただ毎回1つだけというのは並列がができず、またランダム性が大きすぎるので、ミニバッチ毎(1つではなく、少量のデータを使う)に勾配を取ってそこから更新を行うというミニバッチSGDが一般的に使われるSGDになります。
SGDにはさらに「Momentum SGD」と「Nesterov accelerated gradient: NAG」というのがあります。詳細はここでは言及しませんが、ざっくり言うと次のようになります。
- Momentum SGD … SGDはランダム性が大きく、一度一度の勾配の大きさがバラバラである。そこで慣性$v$を追加して勾配の変動を抑え、収束速度を上げる。
- NAG … Momentumでは収束速度は向上するが勾配の向きが必ずしも収束方向に向いているとは限らない。そこで次の重みの位置を先に予測させてから勾配をとることで、勾配の向きを正しい方向に向かわせるようにする。
Momentum SGD:
v_t = \beta v_{t-1}-\eta\nabla_wL(w)\\
w_{t+1} = w_t+v_t
Nesterov (NAG):
v_t = \beta v_{t-1}-\eta\nabla_wL(w-\beta v_{t-1})\\
w_{t+1} = w_t+v_t
tensorflowの場合は、次のように書きます。Momentum, NesterovともにSGDの引数に含まれます(公式ドキュメント)。
sgd = tf.keras.optimizers.SGD(
learning_rate=0.01, # 学習率
momentum=0.0, # momentumのβの値([0-1])。デフォルトは0なので、momentumは無効
nesterov=False # nesterovを適用するかどうか。デフォルトは無効
)
モデルをコンパイルするときは、strで書き込んでもokです。ただし、デフォルトパラメータになるのでこのときのSGDはMomentumもNesterovも適用されません。
model.compile(optimizer='sgd', #デフォルトはmomentumが適用されたSGD
loss='binary_crossentropy',
metrics=['accuracy'])
RMSProp
RMSPropは「勾配の大きさに応じて学習率を調整する」というものです。Momentum SGDは慣性を導入して収束速度を上げますが、こちらは学習率に焦点を当てています。式にすると、次のような感じです。
c_t = \rho c_{t-1} + (1-\rho)\{L(w)\}^2\\
v_t = \beta v_{t-1}-\eta\nabla_wL(w)\\
w_{t+1} = w_t + \frac{v_t}{\sqrt{c_t}+\epsilon}
$\rho$は通常0.9や0.99ほどの値です。$\epsilon$はゼロ除算を回避するためにあって、通常$10^{-7}$以下です。$v_t$はSGDで述べたMomentumそのままです。
tensorflowでは次のように書けます。デフォルト値を使う場合でコンパイルするときはoptimizer='rmsprop'でもokです(公式ドキュメント)。
rmsp = tf.keras.optimizers.RMSprop(
learning_rate=0.001,
rho=0.9,
momentum=0.0,
epsilon=1e-07,
centered=False
)
centeredというのはRMSpropの改善版であるRMSpropGravesを使うかどうかの設定のようです。下の記事で詳しく説明されています。
RMSpropGravesについて自分なりに考えてみた
Adaptive Moment Estimation (Adam)
AdamはRMSpropと似ています(そもそも全部SGDの改良ですが)。RMSpropの式の$c_t$では勾配の2乗を用いていましたが、Adamの場合は1乗のものが追加されています。安定性が高いため、SDGと並んで頻繁に使われています。
m_t = \beta_1 c_{t-1} + (1-\beta_1)\nabla_wL(w)\\
v_t = \beta_2 v_{t-1} + (1-\beta_2)\nabla_w\{L(w)\}^2\\
\hat{m}_t=\frac{m_t}{1-{\beta_1}^t}\\
\hat{v}_t=\frac{v_t}{1-{\beta_2}^t}\\
w_{t+1} = w_t + \frac{\hat{m}_t}{\sqrt{\hat{v}_t}+\epsilon}
詳しいことは話が難しくなるので、もし気になる方は下の記事にて詳しく説明されています。
深層学習の最適化アルゴリズム
勾配降下法の最適化アルゴリズムを概観する
tensorflowでは次のように書けます。デフォルト値を使う場合でコンパイルするときはoptimizer='adam'でもokです(公式ドキュメント)。
adam = tf.keras.optimizers.Adam(
learning_rate=0.001,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-07,
)
この他にも、Nesterov+Adamの「NAdam6」や、AdamとSDGのいいとこどりの「AdaBound7」など様々です。
どのオプティマイザを用いるべきか
損失関数ではなく、オプティマイザの場合はどうなのでしょうか。答えを言ってしまうと、今のところこちらも正解はありません。
本記事で挙げたAdamは安定性が高いため非常によく使われていますが、パラメータ設定が悪いとタスクによっては局所解になったり、学習が不安定になります。もちろん、それ以外のOptimizerでも学習率やそのほかの係数が誤った値だと不安定になります。そういったパラメータの最適値を探すために、KerasTunerやOptunaなどを用いたパラメータチューニングが必要になってきます。
ただここまでいくと流石に上級者向けになるので、僕みたいな駆け出しの人だったらまだオプティマイザについてはそこまでこだわる必要はないかなと思います。
4. 実際に試す
実際に、MRIの画像を使ったセグメンテーションを行い、損失関数の違いとオプティマイザの違いを比べてみます。
今回使用するのはKaggleのLGG Segmentation Datasetです。セグメンテーションコードはMonKira氏のコードをこの記事用に少し変えたものとなります。
はじめに必要なモジュールをインポートします。
import glob
import math
import os
import cv2
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow.keras.backend as K
from sklearn.model_selection import train_test_split
from tensorflow.keras.callbacks import (EarlyStopping, ModelCheckpoint,
ReduceLROnPlateau)
from tensorflow.keras.layers import (Activation, BatchNormalization, Conv2D,
Conv2DTranspose, Dropout, Input, Lambda,
MaxPooling2D, concatenate)
from tensorflow.keras.models import clone_model, Model
from tensorflow.keras.optimizers import Adam, RMSprop, SGD
from tensorflow.keras.preprocessing.image import ImageDataGenerator
データセットの中身は以下のようになります。
plt.style.use("ggplot")
DATASET_FOLDER = 'lgg-mri-segmentation/kaggle_3m'
mask_list = [p for p in glob.iglob(DATASET_FOLDER+'/*/*_mask*')]
img_list = [p.replace('_mask', '') for p in mask_list]
#Lets plot some samples
rows,cols=3,3
fig=plt.figure(figsize=(10,10))
for i in range(1,rows*cols+1):
fig.add_subplot(rows,cols,i)
img_path = img_list[i]
msk_path = mask_list[i]
img=cv2.imread(img_path) * 0.6
msk=cv2.imread(msk_path, cv2.IMREAD_GRAYSCALE)
img[:,:,1] = img[:,:,1] + msk*0.4
img = img.astype(np.uint16)
img=cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
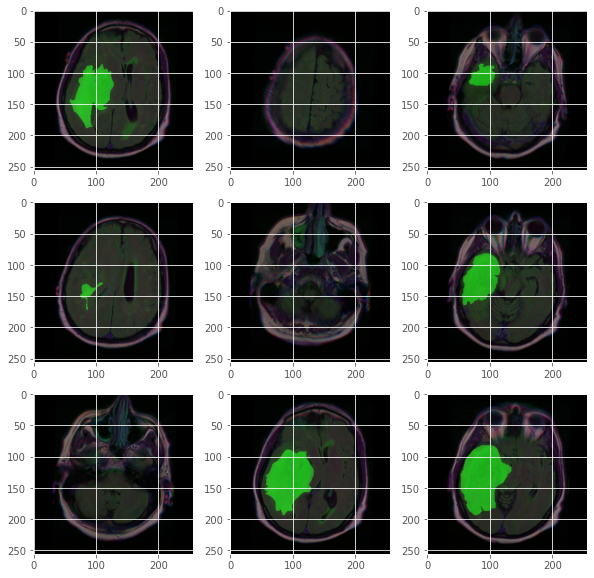
plt.imshow(img)
plt.show()
緑の領域がマスクです。マスクの領域が小さかったり、そもそもないものもありますね。
次にデータを分割します。
df = pd.DataFrame(data={"filename": img_list, 'mask' : mask_list})
df_train, df_test = train_test_split(df,test_size = 0.1)
df_train, df_val = train_test_split(df_train,test_size = 0.2)
print('train:', df_train.values.shape)
print('val:',df_val.values.shape)
print('test',df_test.values.shape)
train: (2828, 2)
val: (708, 2)
test (393, 2)
データ生成関数を作っておきます。
def adjust_data(img,mask):
img = img / 255
mask = mask / 255
mask[mask > 0.5] = 1
mask[mask <= 0.5] = 0
return (img, mask)
def train_generator(data_frame, batch_size, aug_dict,
image_color_mode="rgb",
mask_color_mode="grayscale",
image_save_prefix="image",
mask_save_prefix="mask",
save_to_dir=None,
target_size=(256,256),
seed=1):
'''
From: https://github.com/zhixuhao/unet/blob/master/data.py
Can generate image and mask at the same time use the same seed for
image_datagen and mask_datagen to ensure the transformation for image
and mask is the same if you want to visualize the results of generator,
set save_to_dir = "your path"
'''
image_datagen = ImageDataGenerator(**aug_dict)
mask_datagen = ImageDataGenerator(**aug_dict)
image_generator = image_datagen.flow_from_dataframe(
data_frame,
x_col = "filename",
class_mode = None,
color_mode = image_color_mode,
target_size = target_size,
batch_size = batch_size,
save_to_dir = save_to_dir,
save_prefix = image_save_prefix,
seed = seed)
mask_generator = mask_datagen.flow_from_dataframe(
data_frame,
x_col = "mask",
class_mode = None,
color_mode = mask_color_mode,
target_size = target_size,
batch_size = batch_size,
save_to_dir = save_to_dir,
save_prefix = mask_save_prefix,
seed = seed)
train_gen = zip(image_generator, mask_generator)
for (img, mask) in train_gen:
img, mask = adjust_data(img, mask)
yield (img,mask)
Unetを構築します。他ののUnet(segmentation_models等)も検討しましたが、MonKira氏のUnetに落ち着きました。原因を考えておかないと…
def unet(input_size=(256,256,3)):
inputs = Input(input_size)
conv1 = Conv2D(64, (3, 3), padding='same')(inputs)
bn1 = Activation('relu')(conv1)
conv1 = Conv2D(64, (3, 3), padding='same')(bn1)
bn1 = BatchNormalization(axis=3)(conv1)
bn1 = Activation('relu')(bn1)
pool1 = MaxPooling2D(pool_size=(2, 2))(bn1)
conv2 = Conv2D(128, (3, 3), padding='same')(pool1)
bn2 = Activation('relu')(conv2)
conv2 = Conv2D(128, (3, 3), padding='same')(bn2)
bn2 = BatchNormalization(axis=3)(conv2)
bn2 = Activation('relu')(bn2)
pool2 = MaxPooling2D(pool_size=(2, 2))(bn2)
conv3 = Conv2D(256, (3, 3), padding='same')(pool2)
bn3 = Activation('relu')(conv3)
conv3 = Conv2D(256, (3, 3), padding='same')(bn3)
bn3 = BatchNormalization(axis=3)(conv3)
bn3 = Activation('relu')(bn3)
pool3 = MaxPooling2D(pool_size=(2, 2))(bn3)
conv4 = Conv2D(512, (3, 3), padding='same')(pool3)
bn4 = Activation('relu')(conv4)
conv4 = Conv2D(512, (3, 3), padding='same')(bn4)
bn4 = BatchNormalization(axis=3)(conv4)
bn4 = Activation('relu')(bn4)
pool4 = MaxPooling2D(pool_size=(2, 2))(bn4)
conv5 = Conv2D(1024, (3, 3), padding='same')(pool4)
bn5 = Activation('relu')(conv5)
conv5 = Conv2D(1024, (3, 3), padding='same')(bn5)
bn5 = BatchNormalization(axis=3)(conv5)
bn5 = Activation('relu')(bn5)
up6 = concatenate([Conv2DTranspose(512, (2, 2), strides=(2, 2), padding='same')(bn5), conv4], axis=3)
conv6 = Conv2D(512, (3, 3), padding='same')(up6)
bn6 = Activation('relu')(conv6)
conv6 = Conv2D(512, (3, 3), padding='same')(bn6)
bn6 = BatchNormalization(axis=3)(conv6)
bn6 = Activation('relu')(bn6)
up7 = concatenate([Conv2DTranspose(256, (2, 2), strides=(2, 2), padding='same')(bn6), conv3], axis=3)
conv7 = Conv2D(256, (3, 3), padding='same')(up7)
bn7 = Activation('relu')(conv7)
conv7 = Conv2D(256, (3, 3), padding='same')(bn7)
bn7 = BatchNormalization(axis=3)(conv7)
bn7 = Activation('relu')(bn7)
up8 = concatenate([Conv2DTranspose(128, (2, 2), strides=(2, 2), padding='same')(bn7), conv2], axis=3)
conv8 = Conv2D(128, (3, 3), padding='same')(up8)
bn8 = Activation('relu')(conv8)
conv8 = Conv2D(128, (3, 3), padding='same')(bn8)
bn8 = BatchNormalization(axis=3)(conv8)
bn8 = Activation('relu')(bn8)
up9 = concatenate([Conv2DTranspose(64, (2, 2), strides=(2, 2), padding='same')(bn8), conv1], axis=3)
conv9 = Conv2D(64, (3, 3), padding='same')(up9)
bn9 = Activation('relu')(conv9)
conv9 = Conv2D(64, (3, 3), padding='same')(bn9)
bn9 = BatchNormalization(axis=3)(conv9)
bn9 = Activation('relu')(bn9)
conv10 = Conv2D(1, (1, 1), activation='sigmoid')(bn9)
return Model(inputs=[inputs], outputs=[conv10])
model = unet()
使う損失関数を定義しておきます。メトリクスにはDice係数、感度、特異度を使います。
def tversky_loss(y_true, y_pred):
alpha = 0.3 # FP、FNの重み
smooth = 1. # ゼロ除算回避のための定数
y_true_pos = K.flatten(y_true) # 1次元に畳み込み
y_pred_pos = K.flatten(y_pred) # 同様
tp = K.sum(y_true_pos * y_pred_pos) # TP
fp = K.sum((1 - y_true_pos) * y_pred_pos) # FP
fn = K.sum(y_true_pos * (1 - y_pred_pos)) # FN
score = (tp + smooth)/(tp + alpha * fp + (1-alpha) * fn + smooth) # Tversky係数を計算
return 1. - score
def dice_coeff(y_true, y_pred):
smooth = 1. # ゼロ除算回避のための定数
y_true_pos = K.flatten(y_true) # 1次元に畳み込み
y_pred_pos = K.flatten(y_pred) # 同様
tp = K.sum(y_true_pos * y_pred_pos) # TP
score = (2. * tp + smooth) / (K.sum(y_true_pos) + K.sum(y_pred_pos) + smooth) # Dice係数を計算
return score
def dice_loss(y_true, y_pred):
return 1. - dice_coeff(y_true, y_pred)
def sensitivity(y_true, y_pred):
smooth = 1.
y_true_pos = K.flatten(y_true) # 1次元に畳み込み
y_pred_pos = K.flatten(y_pred) # 同様
tp = K.sum(y_true_pos * y_pred_pos) # TP
fn = K.sum(y_true_pos * (1 - y_pred_pos)) # FN
score = (tp + smooth)/(tp + fn + smooth)
return score
def specificity(y_true, y_pred):
smooth = 1.
y_true_pos = K.flatten(y_true) # 1次元に畳み込み
y_pred_pos = K.flatten(y_pred) # 同様
tn = K.sum((1 - y_true_pos)*(1 - y_pred_pos)) # TN
fp = K.sum((1 - y_true_pos) * y_pred_pos) # FP
score = (tn + smooth)/(tn + fp + smooth)
return score
今回は入力サイズを256x256、エポックは50、バッチサイズは32にします。
SIZE = (256,256)
EPOCHS = 50
BATCH_SIZE = 32
学習用、検証用のジェネレータを作ります。
train_generator_args = dict(rotation_range=0.2,
width_shift_range=0.05,
height_shift_range=0.05,
shear_range=0.05,
zoom_range=0.05,
horizontal_flip=True,
fill_mode='nearest')
train_gen = train_generator(df_train, BATCH_SIZE,
train_generator_args,
target_size=SIZE)
val_gen = train_generator(df_val, BATCH_SIZE,
dict(),
target_size=SIZE)
学習を複数するため、学習用の関数を作っておきます。
def train_model(opt, loss_fn, weight_name='model_weights.h5'):
_model = clone_model(model)
# コールバック
## val_lossが更新されたときだけmodelを保存
mc_cb = ModelCheckpoint(weight_name, verbose=1, save_best_only=True,
save_weights_only=True, mode='min')
## 学習が停滞したとき、学習率を0.2倍に
rl_cb = ReduceLROnPlateau(monitor='loss', factor=0.2, patience=5, verbose=1)
## 学習が進まなくなったら、強制的に学習終了
es_cb = EarlyStopping(monitor='loss', patience=8, verbose=1)
_model.compile(optimizer=opt,
loss=loss_fn,
metrics=[dice_coeff, sensitivity, specificity])
history = _model.fit(
x=train_gen,
steps_per_epoch=math.ceil(len(df_train) / BATCH_SIZE),
batch_size=BATCH_SIZE,
validation_data=val_gen,
validation_steps=math.ceil(len(df_val) / BATCH_SIZE),
epochs=EPOCHS,
callbacks=[mc_cb, rl_cb, es_cb]
)
return _model, history
評価用の関数も作ります。
def plot_history_diff(history_list, history_names, savename='pgraph.png'):
cmap = plt.get_cmap('gist_earth', int(len(history_list)*1.5))
fig, ax = plt.subplots(nrows=4,ncols=2,figsize=(15,30))
def ax_set(fn, args=None, **kwargs):
for s in range(8):
if s < 4:
u, v = tuple(bin(8+s)[-2:])
else:
u, v = tuple(bin(8+s-4)[-2:])
u = int(u)+2
if args is not None:
getattr(ax[int(u), int(v)], fn)(args[s], **kwargs)
else:
getattr(ax[int(u), int(v)], fn)(**kwargs)
ax_set('set_title',
['Train loss vs Epoch',
'Val loss vs Epoch',
'Train dice coeff vs Epoch',
'Val dice coeff vs Epoch',
'Train Sensitivity',
'Val Sensitivity',
'Train Specificity',
'Val Specificity'])
ax_set('set_ylabel', ['Loss']*2+['Dice coeff']*2+['Sensitivity']*2+['Specificity']*2)
ax_set('set_xlabel', ['Epoch']*8)
for i, (_history, history_name) in enumerate(zip(history_list, history_names)):
h = _history.history
plot_option = dict(
marker='',
linestyle='solid',
color=cmap(i),
label=history_name
)
ax_set('plot', [
h['loss'],
h['val_loss'],
h['dice_coeff'],
h['val_dice_coeff'],
h['sensitivity'],
h['val_sensitivity'],
h['specificity'],
h['val_specificity']], **plot_option)
ax_set('legend')
ax_set('set_xlim', [[0,52.5]]*8)
ax_set('set_ylim', [[0,1.05]]*8)
plt.xlabel("Epoch")
plt.savefig(savename)
plt.show()
def show_predictions(models, names):
for i in range(10):
index=np.random.randint(1,len(df_test.index))
img = cv2.imread(df_test['filename'].iloc[index])
img = cv2.resize(img , SIZE)
img = img / 255
img = img[np.newaxis, :, :, :]
pred0=models[0].predict(img)
pred1=models[1].predict(img)
pred2=models[2].predict(img)
plt.figure(figsize=(15,15))
plt.subplot(1,5,1)
plt.imshow(np.squeeze(img))
plt.title('Original Image')
plt.subplot(1,5,2)
plt.imshow(np.squeeze(cv2.imread(df_test['mask'].iloc[index])))
plt.title('Original Mask')
plt.subplot(1,5,3)
plt.imshow(np.squeeze(pred0) > .5)
plt.title(f'Prediction({names[0]})')
plt.subplot(1,5,4)
plt.imshow(np.squeeze(pred1) > .5)
plt.title(f'Prediction({names[1]})')
plt.subplot(1,5,5)
plt.imshow(np.squeeze(pred2) > .5)
plt.title(f'Prediction({names[2]})')
plt.show()
損失関数の比較
今回は、損失関数の比較は2値クロスエントロピー、Dice損失、tversky損失とします。オプティマイザはSGD+Momentum+Nesterovでやってみました。
# bce
model_bce, hist_bce = train_model(SGD(momentum=0.9, nesterov=True), 'binary_crossentropy', 'model_weights_bce.h5')
# dice
model_dice, hist_dice = train_model(SGD(momentum=0.9, nesterov=True), dice_loss, 'model_weights_dice.h5')
# tversky
model_tversky, hist_tversky = train_model(SGD(momentum=0.9, nesterov=True), tversky_loss, 'model_weights_tversky.h5')
学習結果を比較してみます。
plot_history_diff(
[hist_bce, hist_dice, hist_tversky],
['BCE', 'Dice', 'Tversky'],
'bdt.png'
)
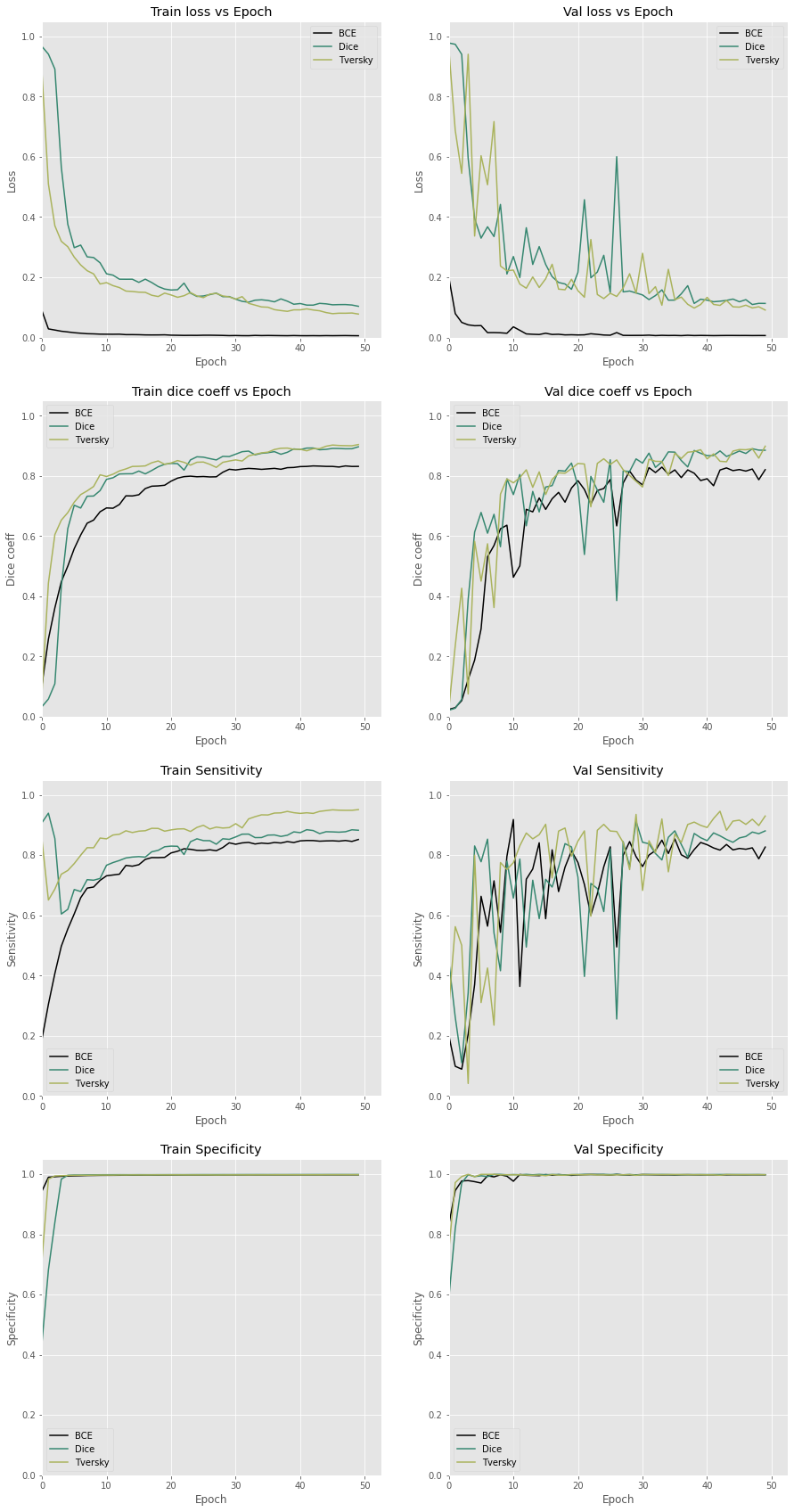
2値クロスエントロピーはほかに比べて初めから損失が小さいですね。微分式とSGDとの相性がいいからでしょうか。一方でメトリクスは他よりも小さくなっていました。
Dice損失とTversky損失はDice係数ではそれほど差はないですが、感度を見るとTverskyの方がスコアが高くなっています。重みづけの効果が表れてますね。
感度についてはどれもほぼ100%くらいです。
テストデータでランダムで何枚か推論してみます。
show_predictions([model_bce, model_dice, model_tversky], ['BCE', 'Dice', 'Tversky'])
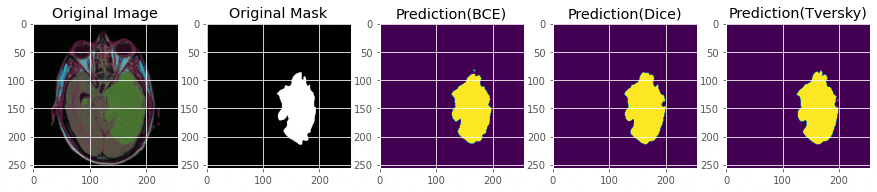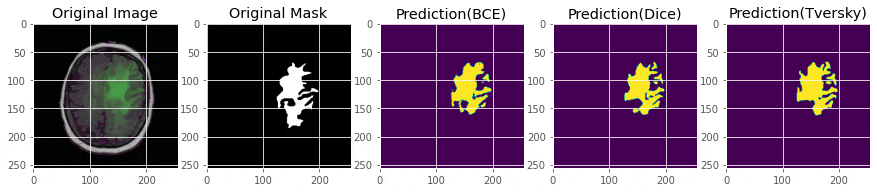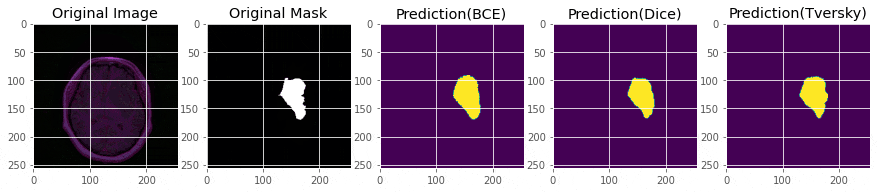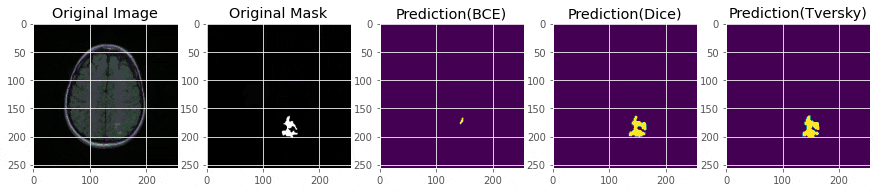
完璧ではないですが、マスクがついている画像ではある程度推論はできています。
オプティマイザの比較
オプティマイザは損失をDice損失として、SGD(+Momentum+Nesterov)、RMSProp、Adamで比較してみます。
# RMSprop
model_rms, hist_rms = train_model(RMSprop(), dice_loss, 'model_weights_rms.h5')
# Adam
model_adam, hist_adam = train_model(Adam(), dice_loss, 'model_weights_adam.h5')
結果:
plot_history_diff(
[hist_dice, hist_rms, hist_adam],
['SGD', 'RMSprop', 'Adam'],
'sra.png'
)
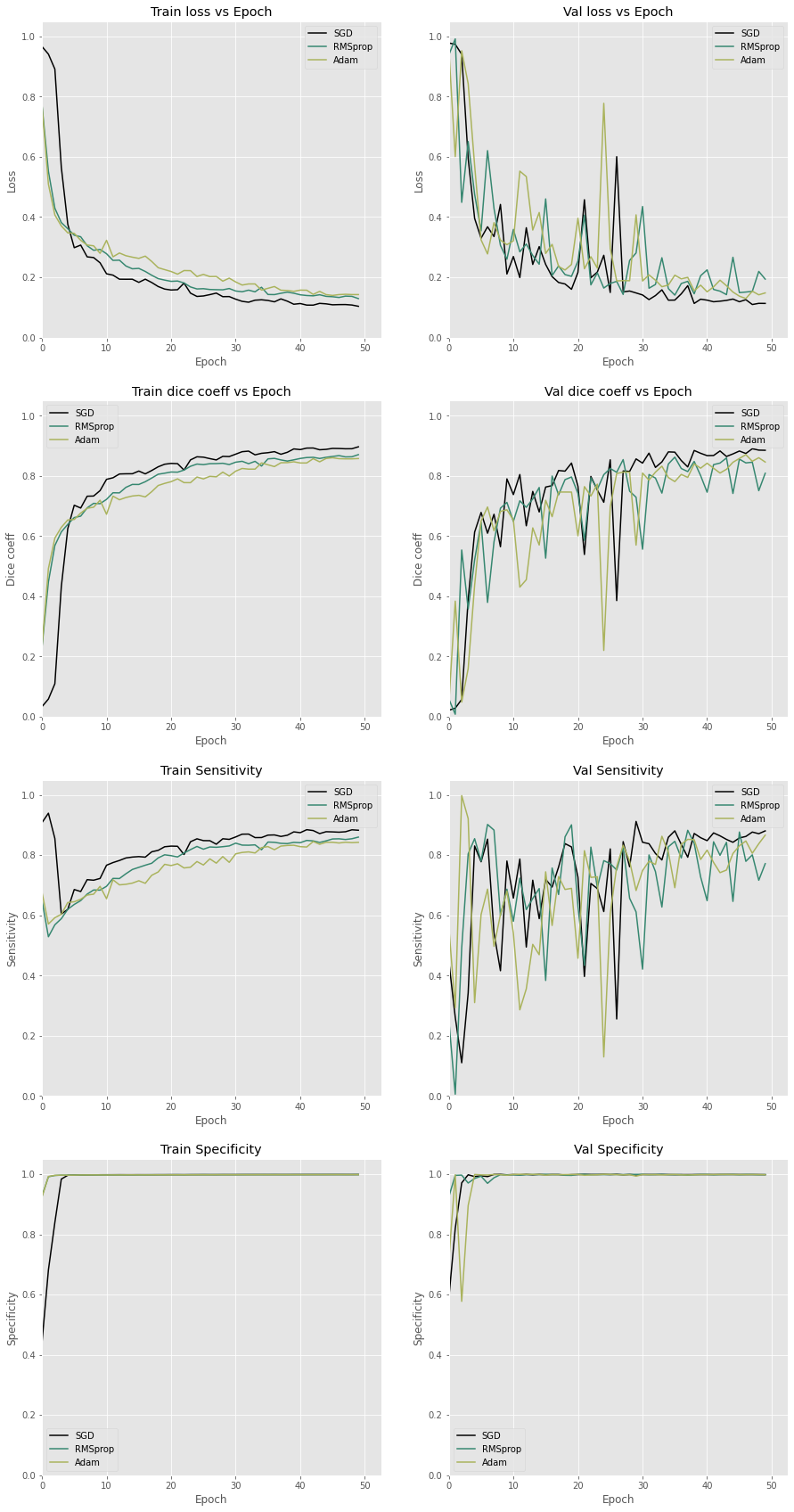
特異度はこちらもほとんど同じですが、それ以外についてはSDGが一番良さそうといった所でしょうか。
RMSpropとAdamはパラメータチューニングはした方がよいとのことなので8、がんばったら今回よりもいい結果が出そうな気がします。
最後に、こちらもランダムで何枚か推論してみます。
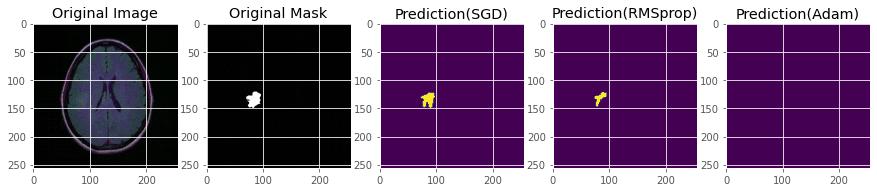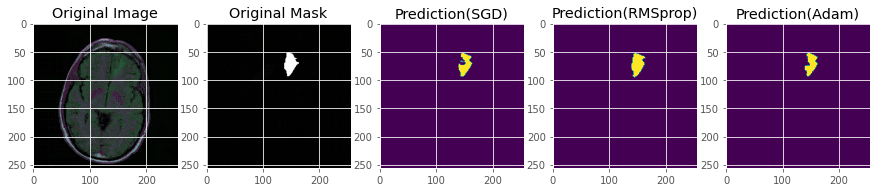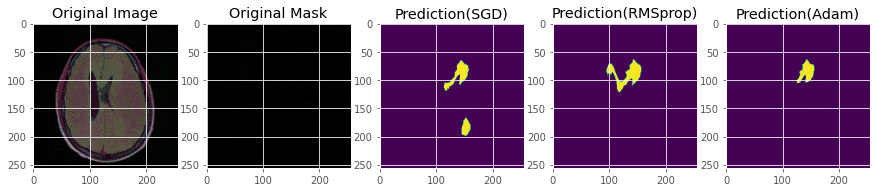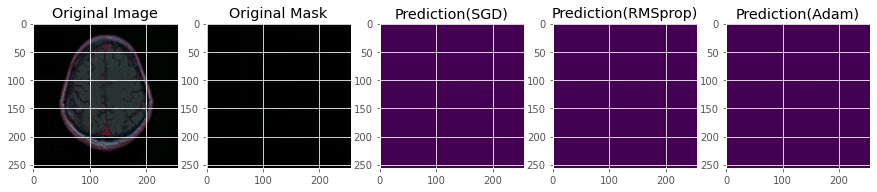
show_predictions([model_dice, model_rms, model_adam], ['SGD', 'RMSprop', 'Adam'])
誤検出があったり、検出できない画像があったりです。うーん、難しい。
おわりに
この記事では損失関数とオプティマイザの紹介、そしてそれらの違いでモデルの精度がどう変化するかを検証しました。この記事で少しでもわかっていただければうれしいです。
まだ自分でもわかってないところが多いので、今後のためにも勉強しておかないとですね…。
その他参考
Lossについて
Optimizerについて
- 【決定版】スーパーわかりやすい最適化アルゴリズム -損失関数からAdamとニュートン法-
- ニューラルネットワークの中をのぞく
- CS231n Convolutional Neural Networks for Visual Recognition
実践
-
Ma Yi-de, Liu Qing, and Qian Zhi-Bai., "Automated image segmentation using improved pcnn model based on cross-entropy"., (IEEE, 2004)
実際に正解値$y$と予測値$\hat{y}$を使って式で表すと、次のようになります。 ↩ -
Fabian Isensee, Jens Petersen, et.al., "nnU-Net: Self-adapting Framework for U-Net-Based Medical Image Segmentation"., (ICCV, TPAMI 2019) ↩
-
Seyed Sadegh Mohseni Salehi, Deniz Erdogmus, Ali Gholipour., "Tversky loss function for image segmentation using 3D fully convolutional deep networks"., (MICCAI 2017 MLMI) ↩
-
Nabila Abraham, Naimul Mefraz Khan., "A Novel Focal Tversky loss function with improved Attention U-Net for lesion segmentation"., (ISBI 2019) ↩
-
勾配降下法とも呼ばれます。英語だとこっちになりますね。 ↩
-
Timothy Dozat., "Incorporating Nesterov Momentum into Adam"., (ICLR 2016) ↩
-
Liangchen Luo, Yuanhao Xiong, Yan Liu, Xu Sun., "Adaptive Gradient Methods with Dynamic Bound of Learning Rate"., (ICLR 2019) ↩