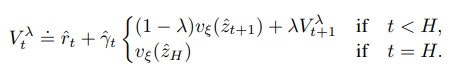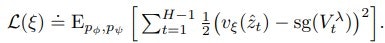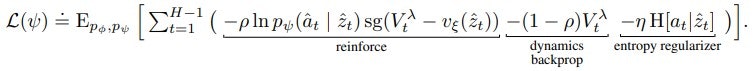この記事は自作している強化学習フレームワークの解説記事です。
DreamerV2
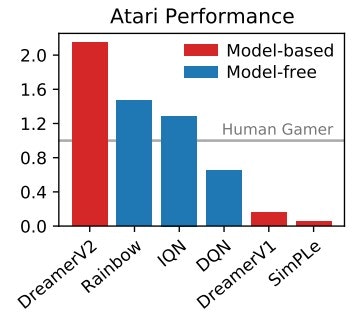
WorldModelシリーズのモデルベース強化学習は面白いアプローチですが、モデルフリー強化学習と比べると特にAtari環境ではパフォーマンスに難がある状況でした。
DreamerV2はDreamerを改良し、Atari環境において人間レベルやRainbowよりも高いパフォーマンスを実現した手法となります。
参考
・論文:https://arxiv.org/abs/2010.02193
・Code: https://github.com/danijar/dreamerv2
・Mastering Atari with Discrete World Models | Google Research
・DreamerV2の実装: 世界モデルベース強化学習でブロック崩し | どこから見てもメンダコ
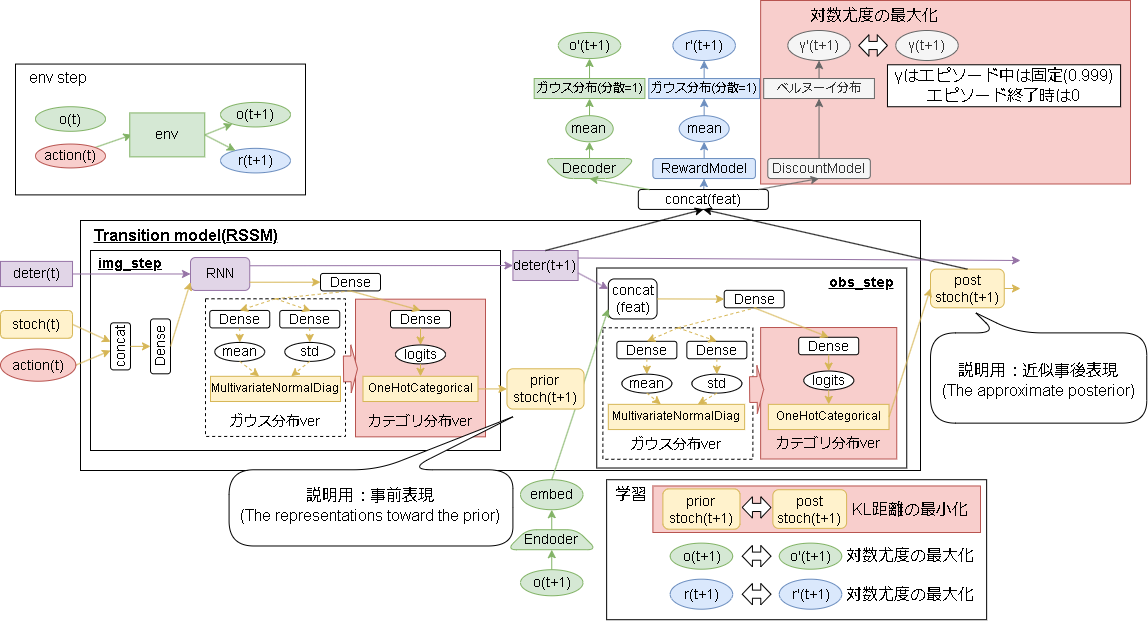
Dreamerとの違い
ベースはDreamerと同じでRSSMから構成されます。(詳細はDreamerの記事を参照)
これに以下3点の変更がされています。
- 内部状態の表現をガウス分布からカテゴリ分布に変更
- KLバランシング
- (Discountの予測の追加)
論文として大きく取り上げられているのはカテゴリ分布とKLバランシングの変更です。
Discountの予測の追加は主題ではなく、実装レベルのテクニックだと思われます。
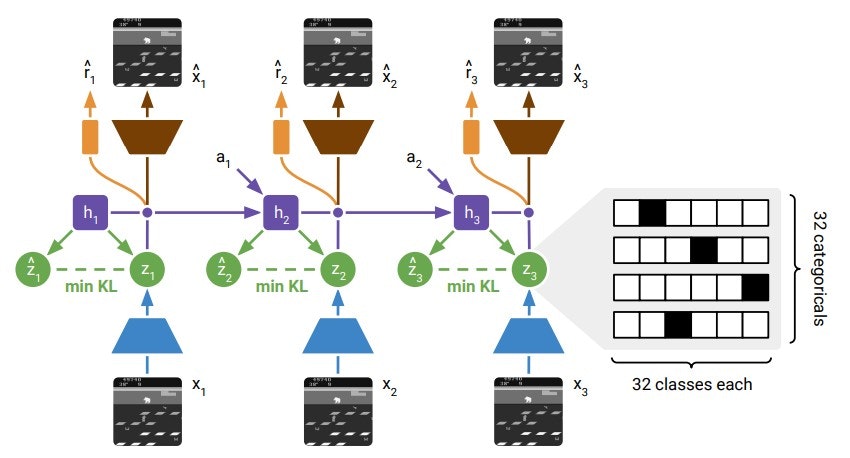
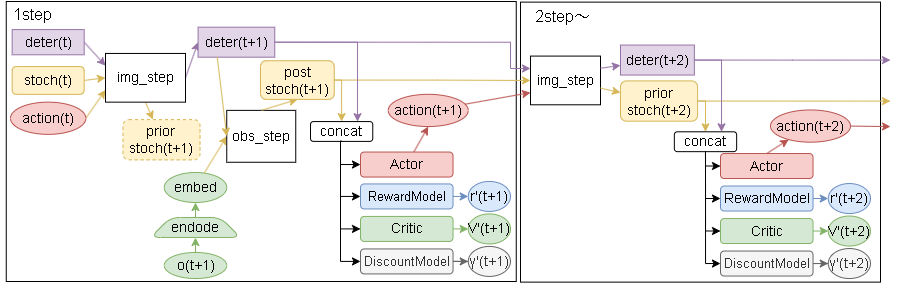
モデルの概要は以下です。
Dreamerとの違いを書いた詳細なモデルは以下です。
Dreamerからの変更部分を赤くしています。
また説明用に、'prior stoch'を事前表現、'post stoch'を近似事後表現と命名します。(いい言葉が書いてなく暫定です…、この記事内のみで使います)
1. 内部状態の表現をガウス分布からカテゴリ分布に変更
Dreamer以前では画像から内部状態を獲得する手法として、VAE(変分オートエンコーダー)+ガウス分布が使われていました。
これをガウス分布ではなくカテゴリ分布に変更しています。
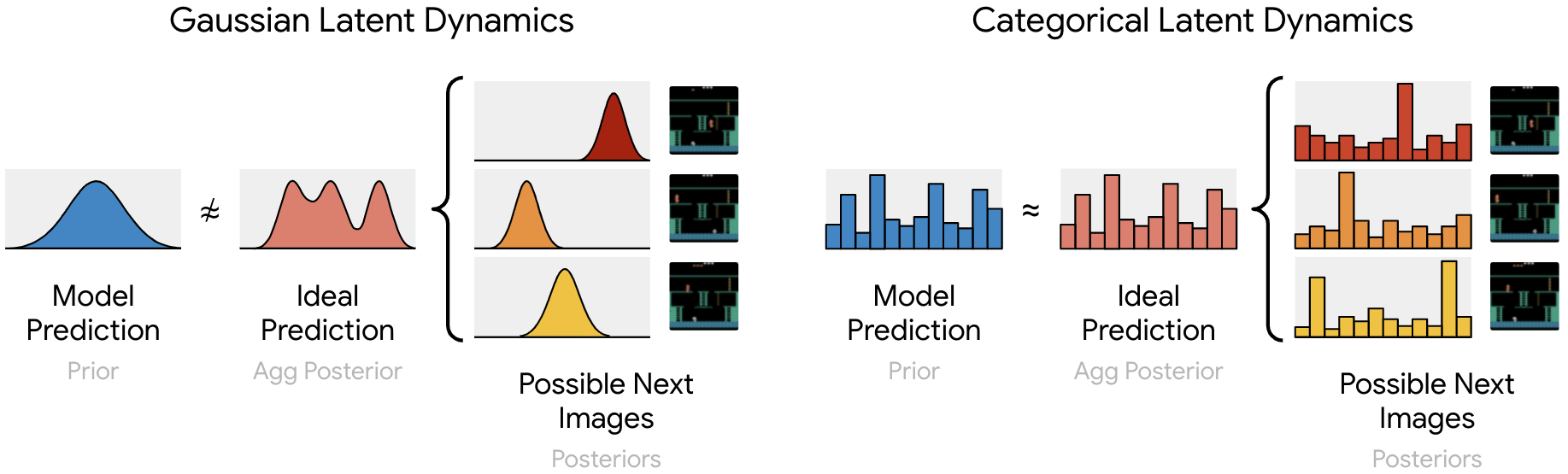
(図はブログより引用)
図の見方ですが、左がガウス分布で右がカテゴリ分布です。
それぞれの図で左(青,Model Prediction)が予測される分布で、真ん中(赤オレンジ:Ideal Prediction)が理想的な分布、右側が実際に予測されるべき次の分布(及び画像)です。
左のガウス分布では山が1つしかないので3種類の画像を表現できません。
しかし、カテゴリ分布だと複数の山を持つことが可能になり、複数の画像を表現できます。1
また、この変更について論文内で言及されている内容は以下です。
- (Atariタスクにて)カテゴリ分布が優れているのが42タスク、ガウス分布が優れているのが8タスク、同程度が5タスク
- カテゴリ分布はカテゴリ分布同士を混ぜてもカテゴリ分布になるが、ガウス分布は混ぜてもガウス分布にはならない(混合ガウス分布になる)ので、変化が複数ある場合に対応できない
→上述の画像と同じ内容を言っていると思います。 - カテゴリ分布による強制的なスパース性が汎化に有益である可能性がある
→連続値であるガウス分布では対象にマッチしすぎて過学習を起こし、カテゴリ分布は離散値なので過学習にはなりにくくなる(汎化性能が上がる)可能性がある、と解釈しました。 - カテゴリ変数はガウス変数よりも最適化が簡単である可能性がある。これはおそらく直線勾配推定器(the straight-through gradient estimator)がスケールする項を無視するため。これにより、勾配の爆発や消滅が減少する可能性がある。
→ガウス変数は平均-∞~∞、分散が0~∞で学習されるがカテゴリ変数は確率(0~1)で学習されるので勾配のスケールが整っており学習が安定するみたいな内容と解釈しました。 - カテゴリ変数は、Atariで新しい部屋に入るや敵が画面から消えるなど連続的ではない変化(the non-smooth aspects)の表現が、ガウス分布による連続的な変化より適している可能性がある
2. KLバランシング
Dreamerでは事前表現(prior stoch)と近似事後表現(post stoch)をKL距離の最小化により学習していました。
この学習には2つの役割があります。
- 近似事後表現はEncoder-Decoder(VAE)に対して学習する(正則化項であり、内部表現を獲得する)
- 近似事後表現を予測できるように事前表現を学習する(画像がない状態の未来の予測)
ここで2の事前表現の学習は状態の遷移を扱うため学習が難しく、あまり訓練されていない事前表現を使いたくありません。
なのでこの問題を解決するために、事前表現と近似事後表現で異なる学習率を使う方法をKLバランシングといいます。
具体的には事前表現を学習率 $\alpha=0.8$、近似事後表現を $1-\alpha=0.2$として学習します。
また、これについて論文内で言及されている内容は以下です。
- (Atariタスクにて)KLバランシングが優れているのが44タスク、逆に低下したのが6タスク、同程度が5タスク
- 事後エントロピーを基準にして事前エントロピーを学習することにより、事後エントロピーを増加させてKLを低減する方向ではなく、より情報に基づいた事後エントロピーに向けて事前エントロピーを改善する方向になる。
- KLバランシングはWorldModelsだけではなく、学習された事前分布を使用する一般的な確率モデルに対しても有益な可能性がある
3. Discountの予測の追加
予測ですが、画像のデコードと報酬の他に新しく割引率(Discount)を予想します。
割引率はベルヌーイ分布であらわされ、エピソード中のステップは固定値(0.999)、エピソード終了時のステップは0で学習されます。
この予測はActor/Criticを学習する際に、未来を予測する時の終了の判断で使われます。
損失関数
discount loss が増えた以外はDreamerと同じです。
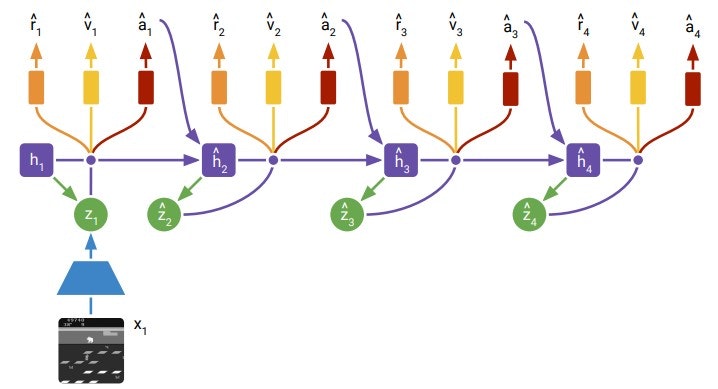
Actor Critic モデル
ここはDreamerとほぼ同じですが、いくつか改善がされています。2
詳細は以下です。
Critic loss function
Dreamerの指数加重平均(Exponentially Weighted Average)より、より一般化されているλ-target(多分TD(λ)法の事だと思います)を使い価値を算出します。
この値に対して損失はMSEで出します。(sgはstop gradientの事で、勾配が流れない事を意味します)
また学習に用いられるネットワークは、パラメータを固定したターゲットネットワークを用いて学習し安定化を図っています。
(100step毎に更新するとのこと)
(DQN等で使用されているターゲットネットワークのことです。ターゲットネットワークについてはこちらの記事を参照)
Actor loss function
Criticで計算されたλ-targetを元に、これを最大化するようにActorは学習されます。
勾配の計算ですが、DreamerV2では3種類の勾配を組み合わせます。
式は以下です。
-
REINFORCE(Reinforce gradients)
式では reinforce の部分で、一般的な強化学習で方策を学習する際の方法(方策勾配法)となります。
利点としてはバイアスがかかっていない勾配が生成できますが、ベースラインを引いても分散が高くなることが欠点です。(方策勾配法/REINFORCEはこちらの記事を参照) -
直接的な逆伝搬(Straightthrough gradients)
式では dynamics backprop の部分で、Dreamerで使用されている方法です。
モデルが微分できることを利用して直接方策を学習します。
欠点としてはバイアスがかかっている勾配が生成されますが、利点としては分散が低くなることです。 -
探索エントロピー
式では entropy regularizer の部分で、Actorのエントロピーを用いて探索を促進する方法です。
正則化項に該当します。(SACで用いられている手法です。記事はこちら)
論文では直感的な解釈としては、2の直接的な逆伝搬は初期学習の効率を高め、1のREINFORCEは局所解から抜け出しより良い解に収束する可能性を高めるとの事でした。
これらを調整する $\rho$ $\eta$ ですが、Atariの場合は1のREINFORCEが有効で $\rho=1$ $\eta=10^{-3}$ 、連続値を制御する場合は逆に2の直接的な逆伝搬が有効で $\rho=0$ $\eta=10^{-4}$ を使うといいとの事です。
また、論文ではこれらの値をアニーリングするとAtariのスコアがよりよくなったとの事ですが、複雑さを回避するために固定値にしているとの事でした。
コード
実装コードはgithubを見てください。
フレームワーク上はDreamerV1/V2/V3を統合してV3だけにしています。
学習
学習コードはこちらを見てください。
WorldModelsよりは学習しやすいイメージを受けました。
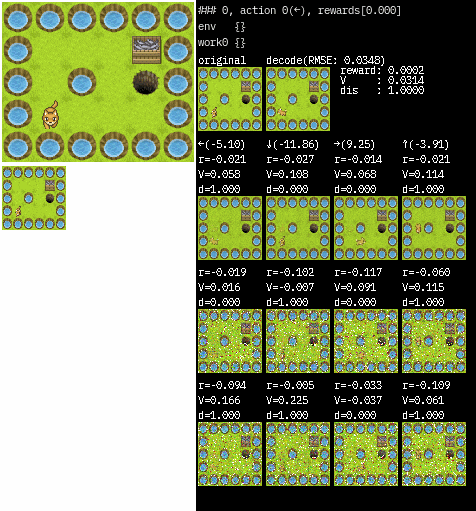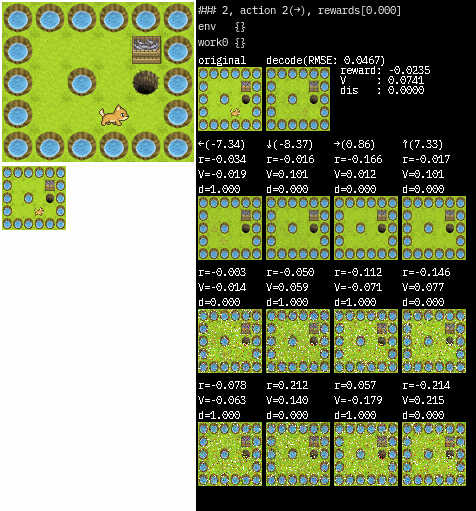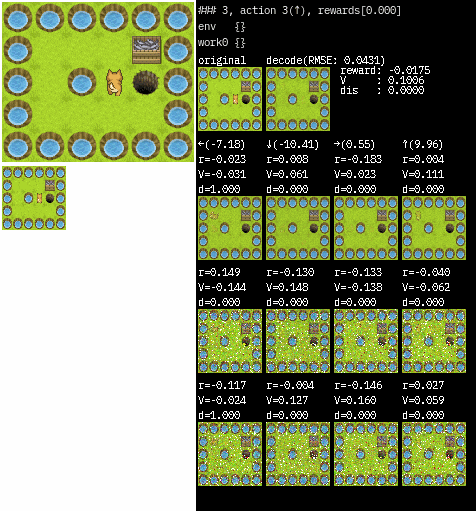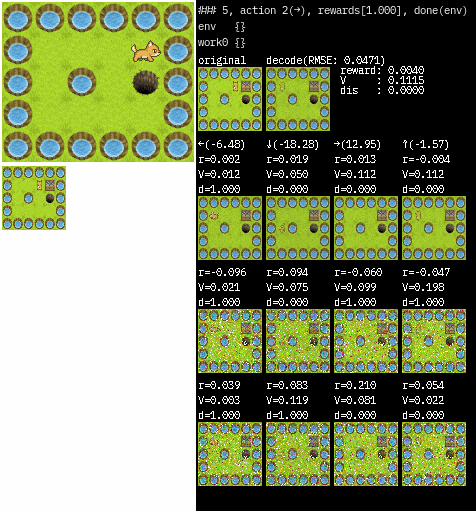
画像は、図の左上がオリジナルの環境で original とあるのがWorkerが受け取る状態です。(64×64にリサイズされた後を受け取っています)
decode は original 画像を VAE を通して復元した結果で、右側の値はそれぞれ予測された値です。
アクションの下にある画像は RSSM を通して予測された次の状態を復元したものです。
復元結果は一番上がmean(平均)を用いた画像で、下2つはランダムに出力した画像です。
カテゴリ分布なので乱数の出力はひどいですが、modeの出力は安定していますね。(少し学習が少なかったかもしれません)
おわりに
WorldModelシリーズはこれで一段落ですね。ほんとかな?