この記事は自作している強化学習フレームワークの解説記事です。
DreamerV3の概要
DreamerV3は、極めて難しいタスクとして知られる Minecraft のダイヤモンド収集タスクを初めてゼロから解いたアルゴリズムとして話題になりました。
論文での内容としては大きく以下となります。
- 出来るだけパラメータを固定し幅広い環境で好成績を収めた
- Minecraftのダイヤモンド収集タスクが実行可能な初めてのアルゴリズム
- モデルが大きいほど性能が良くなる事実を発見した
参考
・Mastering Diverse Domains through World Models(論文)
・コード(github)
・Minecraftでダイヤモンド初収集!世界モデル最新手法 DreamerV3 を解説【無料記事】
さまざまな環境への適応とMinecraftのタスク
以下の図は様々な環境でのDreamerV3と他のアルゴリズムの比較です。
各タスクの概要は以下です。
- Proprio Control Suite: 連続アクションのタスクで単純な移動からロボット制御まで多岐にわたるタスク
- Visual Control Suite: 画像を入力とした連続アクションのタスク
- Atari 100k: Atariゲームで100k step学習
- Atari 200M: Atariゲームで200M step学習
- BSuite: クレジット,報酬スケール,確率性,メモリ,一般化,探索などを評価するためのタスク
- Crafter: 広範囲で広い探索が必要な環境
DreamerV3は連続アクション・離散アクション、画像入力・低次元入力、2D・3Dの世界、異なる報酬における様々な環境で、すべて同じハイパーパラメータを使い好成績を納めていたとの事です。
また、Minecraftのダイヤモンドタスクも攻略したことで話題になりました。
モデルの大きさと性能
図はモデルサイズと学習の比較で、モデルは8Mから200Mのパラメータ数を5段階に分けて比較した結果です。
サイズの大きさに比例して、最終的な性能がいい事(縦軸が高い)が分かります。
また、特筆すべきはサンプル効率も高くなっている(横軸が短い=短いステップで学習する)事です。
最近のLLMの動向と同様に強化学習も大規模モデルが正義となる時代になっていますね…。
DreamerV3
DreamerV3はDreamerV2に様々な工夫を加え、出来るだけヒューリスティックなハイパーパラメータの調整を排除したアルゴリズムとなります。
幸いにも論文内にDreamerV2との違いという項目があるのでそこをベースに見ていきたいと思います。
DreamerV2との変更点
1. Symlog予測
報酬および価値ですが、環境により大きくスケールが異なります。
これをSymlog関数を通して扱いやすいように正規化しようというのがSymlog予測です。1
内容としては勾配計算の改善なので、他の手法にも応用できそうな気がします。
損失勾配の計算において大きい価値を学習する場合、平均二乗誤差を使用すると発散する可能性があり、絶対誤差を利用したHuber誤差を使用すると学習が遅くなる可能性があります。
このジレンマを解決する手法としてSymlog予測を提案しています。
symlog関数とその逆関数のsymexp関数は以下です。
$$
symlog(x) = sign(x) \ln({|x|}+1)
$$
$$
symexp(x) = sign(x) (\exp({|x|})-1)
$$
Symlog予測による損失の計算は以下です。
ニューラルネットワークはsymlog変換された値を使い学習し、学習した値はsymexp関数で元の値に復元して使われます。
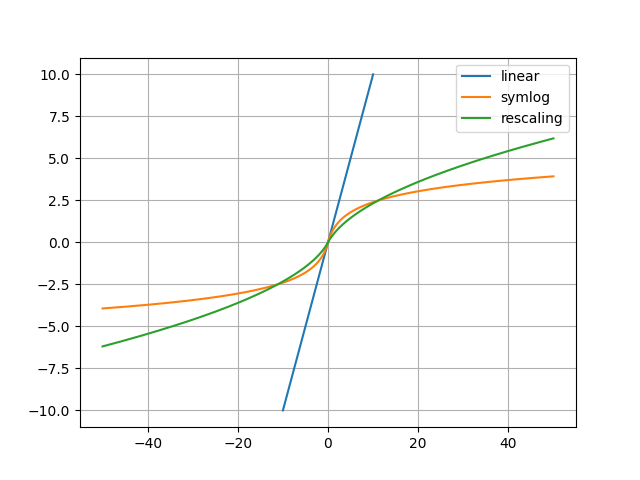
折角なのでrescaling関数と比べてみました。
大きい値は小さい値で学習することで学習を効率化しているようですね。
・コード
import numpy as np
import matplotlib.pyplot as plt
def rescaling(x, eps=0.001):
return np.sign(x) * (np.sqrt(np.abs(x) + 1.0) - 1.0) + eps * x
def inverse_rescaling(x, eps=0.001):
n = np.sqrt(1.0 + 4.0 * eps * (np.abs(x) + 1.0 + eps)) - 1.0
n = n / (2.0 * eps)
return np.sign(x) * ((n**2) - 1.0)
def symlog(x):
return np.sign(x) * np.log(np.abs(x) + 1.0)
def symexp(x):
return np.sign(x) * (np.exp(np.abs(x)) - 1)
x = np.linspace(-10, 10, 10000)
plt.plot(x, x, label="linear")
x = np.linspace(-50, 50, 10000)
y = symlog(x)
plt.plot(x, y, label="symlog")
y = rescaling(x)
plt.plot(x, y, label="rescaling")
plt.legend()
plt.grid()
plt.show()
2. KLの正則化
WorldModelsで正則化項になっているKLの学習ですが、固定値等様々なものを実験した結果、Dreamer(V1)で使われていたfree bitsとDreamerV2で提案されたKLバランシングを組み合わせるのが良いとの事が書かれていました。
free bitsですが、KLダイバージェンスは正則化項なのでこれを完全に学習する(0にする)と学習したい側の学習余地がなくなります。(完全に確率分布と同じになってモデル特有の値にならない)
なのでKLダイバージェンスがある程度以上小さくならないように制限をかける手法がfree bitsとなります。(多分…)
実装上はbitではなくnatという単位を使っています。(bitはlogの底が2ですが、natはlogの底がeの情報量の単位らしいです: 1bit≒1.44nat)
・https://github.com/hardmaru/WorldModelsExperiments/issues/8
・free bitsの記載がある論文
3. Policyの正則化と正規化
損失関数(Actor)で説明します。
4. Unimixカテゴリ分布
Dreamerで使われている変分オートエンコーダー(VAE)ですが、このKL損失は時々スパイク(損失の急激な上昇)が起こるようで、これがDreamerV3の実験中でも見られたとの事でした。
これを回避するためにカテゴリ分布の出力確率の1%を定数とします。
これにより最低限の確率を保証することで、KL損失のスケールを保証します。
簡単にコードを書くと以下です。
import numpy as np
def softmax(x):
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum(axis=0)
logit = np.array([3.0, 2.0, 999.0, 0.0])
probs = softmax(logit)
# unimix
uniform = np.ones_like(probs) / probs.shape[-1]
unimix_probs = 0.99 * probs + 0.01 * uniform
print(probs) # [0. 0. 1. 0.]
print(unimix_probs) # [0.0025 0.0025 0.9925 0.0025] # 最低限の値が保証されている
5. ニューラルネットワークの拡張
基本はDreamerV2と同じアーキテクチャですが大規模化に対応する変更が入っています。
活性化関数はDreamerV2ではELUを使っていましたが、SiLUに変更されています。
また画像の処理では、大きなカーネルサイズのValidパディングではなく、ストライド2とカーネルサイズ3のSameパディングを使うことで大規模パラメータに対応したとの事でした。
DreamerV2とDreamerV3のEncoder/Decoderの例は以下です。
import numpy as np
import tensorflow as tf
from tensorflow import keras
import tensorflow_probability as tfp
kl = keras.layers
tfd = tfp.distributions
# --- Encoder
class DreamerV2_Encoder(keras.Model):
def __init__(self, cnn_depth=48, cnn_kernels=(4, 4, 4, 4)):
super().__init__()
self.cnn_layers = []
for i, kernel in enumerate(cnn_kernels):
depth = 2**i * cnn_depth
self.cnn_layers.append(kl.Conv2D(depth, kernel, 2, activation="elu"))
self.out_layer = kl.Flatten()
def call(self, x):
for h in self.cnn_layers:
x = h(x)
return self.out_layer(x)
class DreamerV3_Encoder(keras.Model):
def __init__(
self,
img_shape=(64, 64, 3),
depth=48,
res_blocks=2,
resized_image_size=4,
):
super().__init__()
self.img_shape = img_shape
_size = int(np.log2(min(img_shape[-3], img_shape[-2])))
_resize = int(np.log2(resized_image_size))
self.stages = _size - _resize
activation = "silu"
kw: dict = dict(
padding="same",
kernel_initializer=tf.initializers.TruncatedNormal(),
bias_initializer="zero",
)
self.blocks = []
for i in range(self.stages):
# --- cnn
cnn_layers = [
kl.Conv2D(depth, 4, 2, use_bias=False, **kw),
kl.LayerNormalization(),
kl.Activation(activation),
]
# --- res
res_blocks_layers = []
for _ in range(res_blocks):
res_layers = [
kl.LayerNormalization(),
kl.Activation(activation),
kl.Conv2D(depth, 3, 1, use_bias=True, **kw),
kl.LayerNormalization(),
kl.Activation(activation),
kl.Conv2D(depth, 3, 1, use_bias=True, **kw),
]
res_blocks_layers.append(res_layers)
self.blocks.append([cnn_layers, res_blocks_layers])
depth *= 2
self.out_layers = []
if res_blocks > 0:
self.out_layers.append(kl.Activation(activation))
self.out_layers.append(kl.Flatten())
# get resized_img_shape
dummy, img_shape = self.call(np.zeros((1,) + img_shape), return_size=True)
self.resized_img_shape = img_shape[1:]
self.out_size = dummy.shape[1]
def call(self, x, return_size=False):
x = x - 0.5
for block in self.blocks:
# --- cnn
for h in block[0]:
x = h(x)
# --- res
for res_blocks in block[1]:
skip = x
for h in res_blocks:
x = h(x)
x += skip
x_out = x
for h in self.out_layers:
x_out = h(x_out)
if return_size:
return x_out, x.shape
else:
return x_out
# --- Decoder
class DreamerV2_Decoder(keras.Model):
def __init__(self, depth: int = 32):
super().__init__()
self.in_layer = kl.Dense(32 * depth)
self.reshape = kl.Reshape([1, 1, 32 * depth])
self.c1 = kl.Conv2DTranspose(4 * depth, 5, 2, activation="relu")
self.c2 = kl.Conv2DTranspose(2 * depth, 5, 2, activation="relu")
self.c3 = kl.Conv2DTranspose(1 * depth, 6, 2, activation="relu")
self.c4_mean = kl.Conv2DTranspose(3, 6, 2)
def call(self, x):
x = self.in_layer(x)
x = self.reshape(x)
x = self.c1(x)
x = self.c2(x)
x = self.c3(x)
x_mean = self.c4_mean(x)
dist = tfd.Normal(x_mean, 1)
return tfd.Independent(dist, reinterpreted_batch_ndims=len(x.shape) - 1)
class DreamerV3_Decoder(keras.Model):
def __init__(
self,
encoder: DreamerV3_Encoder,
use_sigmoid: bool = False,
depth: int = 96,
res_blocks: int = 0,
activation = "silu",
):
super().__init__()
self.use_sigmoid = use_sigmoid
self.dist_type = dist_type
stages = encoder.stages
depth = depth * 2 ** (encoder.stages - 1)
img_shape = encoder.img_shape
resized_img_shape = encoder.resized_img_shape
# --- in layers
self.in_layer = kl.Dense(resized_img_shape[0] * resized_img_shape[1] * resized_img_shape[2])
self.reshape_layer = kl.Reshape([resized_img_shape[0], resized_img_shape[1], resized_img_shape[2]])
# --- conv layers
_conv_kw: dict = dict(
kernel_initializer=tf.initializers.TruncatedNormal(),
bias_initializer="zero",
)
self.blocks = []
for i in range(encoder.stages):
# --- res
res_blocks_layers = []
for _ in range(res_blocks):
res_layers = []
res_layers.append(kl.LayerNormalization())
res_layers.append(kl.Activation(activation))
res_layers.append(kl.Conv2D(depth, 3, 1, padding="same", **_conv_kw))
res_layers.append(kl.LayerNormalization())
res_layers.append(kl.Activation(activation))
res_layers.append(kl.Conv2D(depth, 3, 1, padding="same", **_conv_kw))
res_blocks_layers.append(res_layers)
if i == stages - 1:
depth = img_shape[-1]
else:
depth //= 2
# --- cnn
cnn_layers = [kl.Conv2DTranspose(depth, 4, 2, use_bias=False, padding="same", **_conv_kw)]
cnn_layers.append(kl.LayerNormalization())
cnn_layers.append(kl.Activation(activation))
self.blocks.append([res_blocks_layers, cnn_layers])
self.out_layer = kl.Dense(depth)
def call(self, x):
x = self.in_layer(x)
x = self.reshape_layer(x)
for block in self.blocks:
# --- res
for res_blocks in block[0]:
skip = x
for h in res_blocks:
x = h(x)
x += cast(Any, skip)
# --- cnn
for h in block[1]:
x = h(x)
if self.use_sigmoid:
x = tf.nn.sigmoid(x)
else:
x = cast(Any, x) + 0.5
return self.out_layer(x)
6. Critic EMA 正則化
損失関数(Critic)で説明します。
7. Replay buffer
DreamerV2は完了したエピソードのステップのみを使用していました。(エピソードをまたぐシーケンス長はない)
DreamerV3はエピソードの境界に関係なくシーケンス長を利用し、フィードバックループを短縮するとの事。
(学習バッチの項目で詳細に解説します)
DreamerV3について
変更点以外の点を説明していきます。
損失関数(WorldModel)
DreamerV2とほとんど同じですが各項目の比率が少し変わっています。
DreamerV2の損失関数は以下で、$\beta$ が0.1(Atari)または1.0(連続制御)で更にKL lossがKLバランシングにより8:2に分割されます。
DreamerV3の損失関数はまず以下の3つを定義します。
$L_{pred}$ はDreamerV2の1,2,3項を合わせたものと同じで画像,報酬,継続フラグを予測します。
※DreamerV2では割引率(discount)でしたが、DreamerV3では継続フラグ(Continue $\in{0,1}$)に変更になっています
$L_{dyn}$と$L_{rep}$ はKL損失項のKLバランシングを明示的に分けたものになり、$L_{dyn}+L_{rep}$がDreamerV2のKL lossにあたります。
$max(1,KL損失)$ は「2. KLの正則化」で説明した free bits の実装です。
上記3つの項目を $\beta_{pred}=1$ $\beta_{dyn}=0.5$ $\beta_{rep}=0.1$ の比率で足したものが損失となります。
$L_{pred}:L_{dyn}:L_{rep}$ がV2では 10:8:2 or 10:0.8:0.2 だったのに対し、V3では 10:5:1 になっています。
損失関数(Critic)
DreamerV2ではλ-returnに対してMSE(線形回帰)で学習をしていました。
しかしこれは潜在的に広く分布している期待値を予測するため、学習が遅くなる可能性があるとの事。
そこでV3ではTwoHotエンコーディングを用いた離散回帰のアプローチを行うことで改善しています。
具体的にはsymlog関数で変換された値に対して、K=255個の等間隔のバケットに-20から20の範囲でTwoHotエンコードします。
TwoHotエンコーディングは、小数をカテゴリに分割するテクニックで、小数を隣接する二つの整数に対して重みづけして変換する手法です。
(Muzeroでも使われているテクニックです)
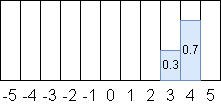
例えば3.7は、隣接する二つの整数(3,4)に対して(0.3, 0.7)と重みづけされます。
これは重みを掛けると元に復元できます。($3 \times 0.3 + 4 \times 0.7 = 3.7$)
TwoHotエンコーディングされた分布に対し、カテゴリクロスエントロピーの最小化を学習します。
またこの離散化はRewardに対しても行っているとの事です。
・論文内にて
論文に書かれている内容を抜粋します。
- TwoHotエンコーディングは特に報酬がまばらな環境で学習が加速する傾向があったとのことです。
これはおそらく二峰性の報酬と収益の(離散的な?)分布のためとの事です。 - λ-returnはCritic自身の予測も含まれているので、これが正則化として学習が安定するとの事です。これはDQNで使われるターゲットネットワークに似ているとの事。
- Criticの初期値はランダムだと予測値が大きくなる可能性がある事に気づいたとの事。初期値を0にすることで学習が早くなったとの事です。
TwoHotエンコーディングのコード例は以下です。
import numpy as np
def twohot_encode(x, bins, low, high):
x = np.clip(x, a_min=low, a_max=high)
arr = np.zeros(bins)
# 0-bins のサイズで正規化
x = (bins - 1) * (x - low) / (high - low)
# 整数部:idx 小数部:weight
idx = np.floor(x).astype(int)
w = x - idx
arr[idx] = 1 - w
if idx + 1 < bins:
arr[idx + 1] = w
return arr
def twohot_decode(x, bins, low, high):
x = np.dot(x, np.arange(0, bins))
return (x / (bins - 1)) * (high - low) + low
x = twohot_encode(3.7, 11, -5, 5)
print(x) # [0. 0. 0. 0. 0. 0. 0. 0. 0.3 0.7 0. ]
y = twohot_decode(x, 11, -5, 5)
print(y) # 3.6999999999999993
Critic値(λ-return)の計算
V2から変更はないですが、備忘録も兼ねてコード例を書いておきます。
horizon = 予測step数
horizon_reward = 予測された報酬
horizon_v = 予測されたV
# shape : (horizon_step, batch_size, 1)
if method == "simple":
# V1に記載がある最も簡単な方法(報酬の合計)
V = tf.reduce_sum(horizon_reward, axis=0)
elif method == "dreamer_v1":
# 指数加重平均(EWA)
discount = 0.999
disclam = 0.1
VN = []
v = tf.zeros((batch, 1), dtype=tf.float32)
for t in reversed(range(horizon)):
v = horizon_reward[t] + horizon_v[t] + discount * v
VN.insert(0, v)
V = VN[0]
for t in range(1, horizon):
V = (1 - disclam) * V + disclam * VN[t]
elif method in ["dreamer_v2", "dreamer_v3"]:
# λ-return
discount = 0.997
h = 0.95
V = tf.zeros((batch, 1), dtype=tf.float32)
for t in reversed(range(horizon)):
V = horizon_reward[t] + discount * (1 - h) * horizon_v[t] + h * V
損失関数(Actor)
DreamerV2では以下の3つの項がありました。
- 直接収益Vの最大化
- Reinforceの方策によるVの最大化
- エントロピー項による正則化
V3では1と3の項のみとなり、2項は閉じた形式で計算されるとの事です。
(ここのcloseの意味があまり分かっていません。1項で間接的に学習されるので問題ないということ? 原文: "The gradient of the second term is computed in closed form.")
この3項においてV3ではエントロピー項に対してメインに改善を行い、以下のアプローチで値を調整しています。2
このエントロピー項の規模ですが環境の報酬の規模に大きく依存し、収益とエントロピーのスケールが安定しません。
報酬が密な環境では単純に標準偏差で割る事で収益を正規化できますが、報酬が疎な環境では標準偏差が小さくなり、その状態で割るとノイズが増幅され探索に失敗します。
そこで、疎でも密でも対応できる手法をV3では提案しています。
方法は単純で、収益の正規化を1以上の場合のみに限定します。
この単純な変更で、報酬が密と疎の両方の場合で収益とエントロピーのスケールを合わせる事が出来るとの事です。
Actorの損失計算式は以下です。
第1項が収益の合計で第2項がエントロピー項です。
$S$がスケールを表し、1とのmaxを取ることで正規化をしています。3
肝心の$S$の計算方法は以下です。
バッチで計算された全ての価値($R_t^{\lambda}$)に対して、95パーセンタイルと5パーセンタイルを使って計算されます。
損失を計算するコード例は以下です。(V1,V2,V3を比較として書いています)
horizon_v = horizonステップで予測したV値
horizon_logpi = horizonステップの各アクションの確率のlog値
horizon_V = horizonステップに対して計算されたλ-returnの値(数式だとRtλ)
# shape : (horizon_step, batch_size, 1)
if self.config.actor_loss_type == "dreamer_v1":
# DreamerV1は単純にVを最大化
loss = -tf.reduce_mean(tf.reduce_sum(horizon_V, axis=0))
elif self.config.actor_loss_type == "dreamer_v2":
reinforce_rate = 1.0 # 連続空間は0.0
entropy_rate = 2e-3
# reinforce
adv = horizon_V - horizon_v
rein_loss = horizon_logpi * tf.stop_gradient(adv)
# dynamics backprop
dyn_loss = horizon_V
# entropy
entropy_loss = -horizon_logpi
loss = -reinforce_rate*rein_loss -(1-reinforce_rate)*dyn_loss - entropy_rate*entropy_loss
loss = tf.reduce_mean(tf.reduce_sum(loss, axis=0))
elif self.config.actor_loss_type == "dreamer_v3":
entropy_rate = 3e-4
# パーセンタイルの計算
d5 = tfp.stats.percentile(horizon_V, 5)
d95 = tfp.stats.percentile(horizon_V, 95)
horizon_V = horizon_V / tf.maximum(1.0, d95 - d5)
v_loss = horizon_V
entropy_loss = -horizon_logpi
loss = -v_loss - entropy_rate*entropy_loss
loss = tf.reduce_mean(tf.reduce_sum(loss, axis=0))
学習のバッチ
バッチの取り扱いについて特に論文に記載がないので理解に苦労しています…。
多分DreamerV2から私の解釈が間違っていたような気がします…。
公式コードでDreamerV2がバッチ内でRNNの隠れ状態を持っていないことが疑問でした。
(これだとエピソード途中からのデータで学習ができない)
DreamerV3の公式コードを見ていたらなんと学習をまたいで隠れ状態を保持していました。
この結果よりエピソード単位での学習は以下なのかと予想しています。4
イメージは以下です。
V1では1エピソード長=バッチ長です。
V2では1エピソードにDummyステップを挿入して同じ長さにし、バッチ長毎に学習します。
V3ではエピソードをまたいでバッチを作成します。エピソードの区切りではRNNの隠れ状態を初期化します。
V3のコード例は以下です。
batch_sequence_list = [[] for _ in range(batch_size)]
batch_sequence_cont = [[] for _ in range(batch_size)]
stoch, deter = 初期隠れ状態
# train loop
while True:
# --- create sequence batch
# 各batchにbatch_seq溜まるまでエピソードを追加する
seq = []
conts = []
for i in range(batch_size):
while len(batch_sequence_list[i]) < (batch_length):
# ランダムに1エピソード取り出す
batch = memory.sample(1) # (batch_size, batch_length, data)
batch_sequence_list[i].extend(batch[0])
# エピソードの区切りを保存
batch_sequence_cont[i].extend([1 for _ in range(episode_len - 1)] + [0])
# batch_length分取り出す
seq.append(batch_sequence_list[i][: batch_length])
batch_sequence_list[i] = batch_sequence_list[i][batch_length :]
conts.append(batch_sequence_cont[i][: batch_length])
batch_sequence_cont[i] = batch_sequence_cont[i][batch_length :]
# --- train RSSM
# (batch, seq, data) -> (seq, batch, data)
seq = tf.transpose(seq, [1, 0, 2])
conts = tf.transpose(conts, [1, 0, 2])
with tf.GradientTape() as tape:
for i in range(batch_length):
# RSSM step で stoch,deter(隠れ状態) を更新
stoch, deter = RSSM.step(stoch, deter, seq[i].action)
# 終了では隠れ状態を初期化
stoch = stoch * conts[i]
deter = deter * conts[i]
(その他いろいろ計算)
コード
コードはgithubを見てください。
フレームワーク上はDreamerV1/V2/V3を統合してV3だけにしました。
学習結果
"Pendulum-v1"が無事に学習できました。
学習バッチを見直したのが一番大きい気がします…。
使用コード
※SRLがv0.14.0のコードです。バージョンが進むと動かない可能性があります。
import os
import srl
from srl.algorithms import dreamer_v3
def train_Pendulum():
env_config = srl.EnvConfig("Pendulum-v1")
rl_config = dreamer_v3.Config()
rl_config.set_dreamer_v3()
# model
rl_config.rssm_deter_size = 64
rl_config.rssm_stoch_size = 4
rl_config.rssm_classes = 4
rl_config.rssm_hidden_units = 512
rl_config.reward_layer_sizes = (256,)
rl_config.cont_layer_sizes = (256,)
rl_config.critic_layer_sizes = (128, 128)
rl_config.actor_layer_sizes = (128, 128)
rl_config.encoder_decoder_mlp = (64, 64)
# lr
rl_config.batch_size = 32
rl_config.batch_length = 15
rl_config.lr_model.set_constant(0.0001)
rl_config.lr_critic.set_constant(0.0001)
rl_config.lr_actor.set_constant(0.00002)
rl_config.horizon = 5
# memory
rl_config.memory.warmup_size = 50
rl_config.memory.capacity = 10_000
rl_config.encoder_decoder_dist = "linear"
rl_config.free_nats = 0.1
rl_config.warmup_world_model = 1_000
# --- train
runner = srl.Runner(env_config, rl_config)
runner.train(max_train_count=30_000)
path = os.path.join(os.path.dirname(__file__), "_dreamer_Pendulum.gif")
runner.animation_save_gif(path)
runner.replay_window()
if __name__ == "__main__":
train_Pendulum()
また、他のアルゴリズムと比較してみました。
"Pendulum-v1"は規模が小さい環境なのでアルゴリズムの比較ではあまり良くない環境ではありますが…
ここでDQNだけアクションが離散空間、他の4つが連続空間で学習しています。
DQNとDreamerV1が同じぐらいの学習傾向ですね。ただV1は安定しないイメージです。
V2は学習できていませんが環境との相性が悪いか、ハイパーパラメータが適切ではないような気がします。
V3はDDPGとSACの中間あたりの傾向でしょうか。
PPOは学習できませんでした。
使用コード
※SRLがv0.14.0のコードです。バージョンが進むと動かない可能性があります。
import os
import numpy as np
import srl
from srl.algorithms import dqn, dreamer_v3, sac
base_dir = os.path.dirname(__file__)
ENV_NAME = "Pendulum-v1"
BASE_TRAIN = 200 * 200
BASE_LR = 0.001
BASE_BLOCK = (64, 64)
def _run(name, rl_config):
runner = srl.Runner(ENV_NAME, rl_config)
runner.set_history_on_file(
os.path.join(base_dir, f"_{ENV_NAME}_{name}"),
enable_eval=True,
eval_episode=10,
)
runner.train(max_train_count=BASE_TRAIN)
rewards = runner.evaluate()
print(f"[{name}] evaluate episodes: {np.mean(rewards)}")
def main_dqn():
rl_config = dqn.Config()
rl_config.lr.set_constant(BASE_LR)
rl_config.hidden_block.set_mlp(BASE_BLOCK)
rl_config.memory.capacity = 10_000
rl_config.memory.warmup_size = 1000
_run("DQN", rl_config)
def main_ppo():
rl_config = ppo.Config()
rl_config.lr.set_constant(BASE_LR)
rl_config.hidden_block.set_mlp(BASE_BLOCK)
rl_config.policy_block.set_mlp(BASE_BLOCK)
rl_config.value_block.set_mlp(BASE_BLOCK)
rl_config.memory.capacity = 10_000
rl_config.memory.warmup_size = 1000
_run("PPO", rl_config)
def main_ddpg():
rl_config = ddpg.Config(lr=BASE_LR)
rl_config.policy_block.set_mlp(BASE_BLOCK)
rl_config.q_block.set_mlp(BASE_BLOCK)
rl_config.memory.capacity = 10_000
rl_config.memory.warmup_size = 1000
_run("DDPG", rl_config)
def main_sac():
rl_config = sac.Config(lr_policy=BASE_LR, lr_q=BASE_LR)
rl_config.policy_hidden_block.set_mlp(BASE_BLOCK)
rl_config.q_hidden_block.set_mlp(BASE_BLOCK)
rl_config.memory.capacity = 10_000
rl_config.memory.warmup_size = 1000
_run("SAC", rl_config)
def main_dreamer(mode):
rl_config = dreamer_v3.Config(lr_model=BASE_LR, lr_critic=BASE_LR, lr_actor=BASE_LR)
if mode == "v1":
rl_config.set_dreamer_v1()
elif mode == "v2":
rl_config.set_dreamer_v2()
elif mode == "v3":
rl_config.set_dreamer_v3()
rl_config.rssm_deter_size = 64
rl_config.rssm_stoch_size = 4
rl_config.rssm_classes = 4
rl_config.rssm_hidden_units = 256
rl_config.reward_layer_sizes = (256,)
rl_config.cont_layer_sizes = (256,)
rl_config.encoder_decoder_mlp = BASE_BLOCK
rl_config.critic_layer_sizes = BASE_BLOCK
rl_config.actor_layer_sizes = BASE_BLOCK
rl_config.batch_size = 32
rl_config.batch_length = 15
rl_config.horizon = 5
rl_config.memory.capacity = 10_000
rl_config.memory.warmup_size = 50
rl_config.free_nats = 0.1
rl_config.warmup_world_model = 1_000
_run("Dreamer_" + mode, rl_config)
def compare():
histories = srl.Runner.load_histories(
[
os.path.join(base_dir, f"_{ENV_NAME}_DQN"),
os.path.join(base_dir, f"_{ENV_NAME}_SAC"),
os.path.join(base_dir, f"_{ENV_NAME}_Dreamer_v1"),
os.path.join(base_dir, f"_{ENV_NAME}_Dreamer_v2"),
os.path.join(base_dir, f"_{ENV_NAME}_Dreamer_v3"),
]
)
histories.plot(
"train",
"eval_reward0",
title=f"Train:{BASE_TRAIN}, lr={BASE_LR}, block={BASE_BLOCK}",
)
histories.plot(
"time",
"eval_reward0",
title=f"Train:{BASE_TRAIN}, lr={BASE_LR}, block={BASE_BLOCK}",
)
if __name__ == "__main__":
main_dqn()
main_ppo()
main_ddpg()
main_sac()
main_dreamer("v1")
main_dreamer("v2")
main_dreamer("v3")
compare()
おわりに
V2に引き続き実装が大変でした…。
デバッグが難しい…
-
R2D2のrescaling関数と似た考えですね。 ↩
-
SACではエントロピー項の係数を自動調整することでアプローチしていましたね。 ↩
-
1で抑えるという手法はretraceにもありますね。あちらはminなので1以下に抑える方法ですけど ↩
-
この学習を使えばR2D2で提案されたBurn-inがいらなくなるのでは?(優先度付きキューが使えなくなりますが…) ↩