この記事は自作している強化学習フレームワーク SimpleDistributedRL の解説記事です。
前:AlphaZero
次1:Stochastic MuZero
次2:EfficientZeroV2
今回はAlphaZeroの後継であるMuZeroについて解説します。
MuZero
AlphaZeroは木探索時にゲームのルールを使うという問題がありました。
(1手進めた後、盤面の状態を知る必要がある)
これではルールを知っている環境にしかAlphaZeroが使えないので、強化学習で一般的に想定されるマルコフ決定過程(MDP)の環境にも使えるように拡張したアルゴリズムがMuZeroです。
(以降本記事で環境を区別する場合、マルコフ決定過程(MDP)の環境をAtari環境、囲碁や将棋などをボードゲーム環境と言って区別します)
MuZeroではゲームのルール自体を学習する事で、ゲームのルールが不明なMDP環境下でも学習を可能にしています。
参考
・MuZeroの実装解説(for Breakout)| どこから見てもメンダコ
・MuZero AIの構築方法
・MuZero: The Walkthrough (Part 1/3)
・Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model
・MuZero論文
・論文の疑似コード: https://arxiv.org/src/1911.08265v2/anc/pseudocode.py
1.MDP環境の表現と学習
MDPを簡単に言うと、次の状態が現在の状態と行動で決まるようなモデルです。(詳細は過去の記事をご覧ください)
MuZeroではMDP環境を表現するために新しく2つのニューラルネットワークを追加しています。
ネットワークの全体像を先に見た方が理解が早いと思うので、まずは各ネットワークとその学習方法について見ていきます。
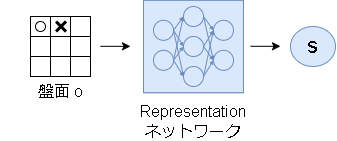
1.表現ネットワーク(Representation network)
表現ネットワークは、環境から観測された状態をアルゴリズム内で使う状態にエンコードする役割があります。
エンコード後の状態自体には特に意味はありません。
(機械学習的に見ると、特徴量抽出の意味合いが強いです)
本記事では区別しやすいように環境から観測された状態を $o$、エンコードされた状態を $s$ と書きます。
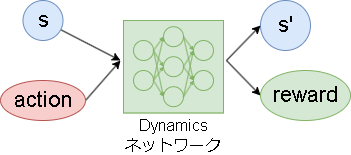
2.ダイナミクスネットワーク(Dynamics network)
ダイナミクスネットワークは今の状態とアクションから次の状態と即時報酬を予測するネットワークです。
※ボードゲーム環境では即時報酬の予測はありません
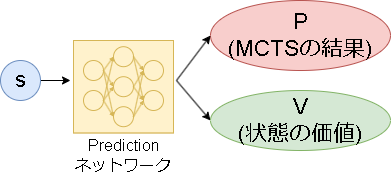
3.予測ネットワーク(Prediction network)
AlphaZeroのPVネットワークとほぼ同じです。(論文に合わせて名前を変えているだけです)
少し違うのは、入力が表現ネットワークでエンコードされた状態 $s$ になっている点です。
ネットワークの学習
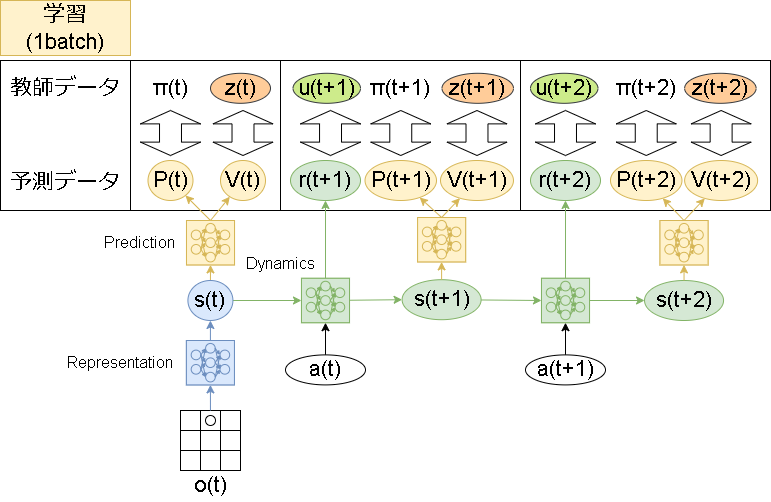
学習ですが、上記3つのネットワークを同時に学習します。
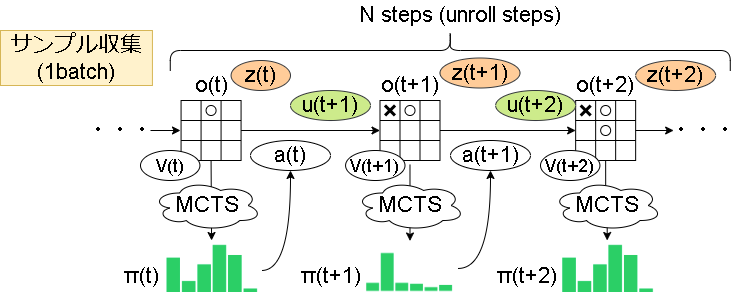
学習用のサンプル収集のイメージは以下です。
記号は、uが即時報酬、zが評価値(AlphaZeroだと勝ち負け)、aがアクション、πがMCTSの結果です。(zの計算方法は後述)
次の状態を学習する必要があるため、展開ステップ(unroll steps)分を1batchとして保存します。
これを元にした学習は以下です。
学習用の損失は3種類あり、それぞれで計算された値の合計が最終的な損失になります。
$$
l_t(\theta) = \sum_{k=0}^K{ l^p(\pi_{t+k}, p_t^k)} + \sum_{k=0}^K{ l^v(z_{t+k}, v_t^k) } + \sum_{k=1}^K{ l^r(u_{t+k}, r_t^k) } + c||\theta||^2
$$
※計算式はMuZeroの次の手法の論文を参考にしています。$l^r$ が間違っていたようで $k=1$ からになっています。
ただ、L2正則化項は明に書いていないようなのでMuZeroにしたがって付けています。
各損失ですが、$l^p$ はAlphaZeroと同様にクロスエントロピーで損失を計算します。
$l^v$ と $l^v$ ですが、ボードゲーム環境はMSEです。
Atari環境ではデータをカテゴリ分布に変換した後にクロスエントロピーで損失を計算します。(カテゴリ分布への変換については後述)
カテゴリ分布に変換する理由は3種類の損失のスケールを合わせるためです。
最後の項はL2正則化項になります。
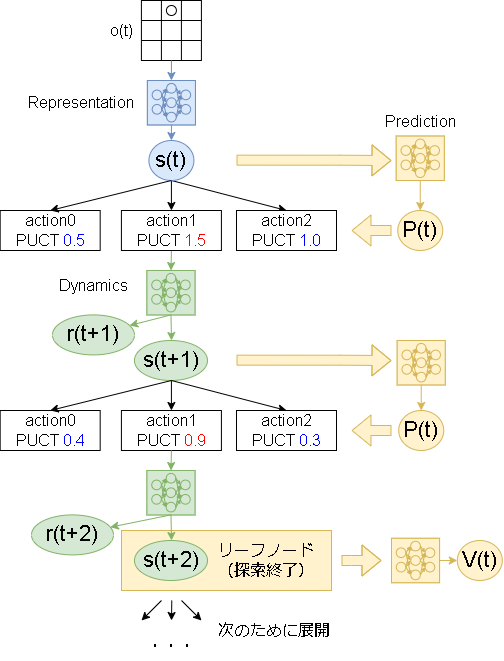
2.MuZero版MCTS
基本はAlphaZeroと同じで、リーフノードまで降りていき盤面の価値を返して展開するだけです。
以下、MCTSの細かい話です。
-
終了状態
MuZeroはAlphaZeroと違って終了状態がないので、リーフノードにたどり着くまで永遠と探索します。
一応、学習時の終了後の状態は吸収状態(absorbing states)として学習されるようです。
参考:吸収マルコフ過程 | 英wikipedia -
価値の伝播
AlphaZeroの実装で既にやっていましたが、Atari環境では報酬を割り引いて伝播させます。
(ボードゲーム環境ではそのまま伝播) -
報酬の反転
こちらも既にやっていますが、ボードゲーム環境では次のstepは相手の手番になるので報酬を反転させます。
(Atari環境では反転なし) -
Root状態でのディリクレノイズ
AlphaZeroから変更せず、ディリクレノイズを追加して探索を促します。 -
有効なアクション
有効なアクションは環境から取得可能なルート状態のみ適用します。
木探索中の有効なアクションは実装せず、ネットワークに学習させます。 -
Q値の正規化
PUCTで使われるQ値ですが、AlphaZeroでは[0,1]の区間を想定していました。
MuZeroでは0~1以外の値を取る可能性があるため、過去観測されたQ値の最小値・最大値で0~1の値に正規化します。
3.その他の話
1.MCTS後のアクションの選択
アクションの選択確率はAlphaZeroと同様以下式で表されます。
$$ p(a) = \frac{N(a)^{1/{\tau}}}{\sum_b N(b)^{1/{\tau}} } $$
$N$ がアクションを選んだ回数で、$\tau$ が温度パラメータです。
ボードゲーム環境は最初の30手は $\tau=1$(回数に従う確率で決定)、それ以降は $\tau \rightarrow 0$(最大回数のアクションを選択)です。
Atari環境では最初の500kステップまでは $\tau=1$、750kステップまでは $\tau=0.5$、以降は $\tau=0.25$ を使います。
2.状態価値(z)の計算
サンプルの収集ででてきた状態価値 z の計算ですが、Atari環境ではNステップの割引報酬を使います。
(Q学習における Multi-step Bootstrapping と同じです)
$$ z_t = u_{t+1} + \gamma u_{t+2} + ... + \gamma^{n-1} u_{t+m} + \gamma^n v_{t+n}$$
$u$ が即時報酬、$\gamma$ が割引率、$v$ が予測価値です。
ただ、フレームワーク上はNをエピソード最後まで展開したモンテカルロ法を採用しています。
3.valueとrewardのrescaling
ValueとRewardのターゲット値にrescaling関数を適用し値を丸めます。(R2D2の手法です)
rescaling関数は以下です。
$$
h(u) = sign(u)(\sqrt{|u|+1}-1) + \epsilon u
$$
$sign$ は符号関数、$\epsilon$ が定数(0.001を使用)です。
4.報酬のカテゴリ分布化
Atari環境は損失のスケールを合わせるために報酬はカテゴリに分けて分布化します。
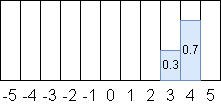
カテゴリ化の方法ですが、ある小数を隣接する二つの整数に対して重みづけして変換します。
例えば3.7は、隣接する二つの整数(3,4)に対して(0.3, 0.7)と重みづけされます。
これは重みを掛けると元に復元できます。($3 \times 0.3 + 4 \times 0.7 = 3.7$)
(小数版one-hotエンコーディングでしょうか)
5.サンプルの優先度
学習に使うサンプルですが、優先度に従って選ばれます。
Rainbowで使われたPrioritized Experience Replayと同じ手法です。
詳細はリンク先を参照してください。
優先度の計算だけ異なり、以下の式で計算されます。
$$p^i = |v_i - z_i|$$
$v$ が予測した状態価値、$z$ がn-steps報酬です。
また、Prioritized Experience Replay のハイパーパラメータですが、$\alpha=\beta=1$ にしているようです。
6.勾配のスケーリング
展開ステップ後の勾配ですが、大きさが揃うようにbackward時の伝播をスケーリングします。
スケール方法は以下です。(疑似コードより)
def scale_gradient(tensor, scale):
"""Scales the gradient for the backward pass."""
return tensor * scale + tf.stop_gradient(tensor) * (1 - scale)
適用箇所は以下です。
- 展開ステップ後の損失を 1/K でスケーリング。(Kは展開ステップ数)
- ダイナミクスネットワークでエンコードされた次の状態(勾配)を 1/2 でスケーリング。
疑似コードより学習の箇所だけを抜粋すると以下です。(見やすいように改変しています)
def update_weights(optimizer, network, batch, weight_decay):
loss = 0
# バッチループ
for init_state, actions, targets in batch:
# --- 1st step
# representation + prediction より P, V, hidden_state を出す
# (reward は予測できないので多分なしだと思う…)
# 最初はスケーリングなし(スケール値=1.0)
value, reward, policy, hidden_state = network.initial_inference(init_state)
predictions = [(1.0, value, reward, policy)]
# --- 展開ステップ
for action in actions:
# dynamics + prediction より P, V, reward, next_hidden_state を出す
value, reward, policy, hidden_state = network.recurrent_inference(hidden_state, action)
# スケール値は 1/K
predictions.append((1.0 / len(actions), value, reward, policy))
# hidden_state は 0.5 でスケールする
hidden_state = scale_gradient(hidden_state, 0.5)
# --- 実際に勾配を計算
for prediction, target in zip(predictions, targets):
gradient_scale, value, reward, policy = prediction
target_value, target_reward, target_policy = target
# 各loss、scalar_loss は MSE(ボードゲーム) or cross_entropy(Atari)
value_loss = scalar_loss(value, target_value)
reward_loss = scalar_loss(reward, target_reward)
policy_loss = cross_entropy(policy, target_policy)
l = (value_loss + reward_loss + policy_loss)
# backwardは各スケール値で
loss += scale_gradient(l, gradient_scale)
# L2正則化項を追加
for weights in network.get_weights():
loss += weight_decay * tf.nn.l2_loss(weights)
optimizer.minimize(loss)
8.エンコード後の状態sのスケーリング
エンコード後の状態sですが、one-hotエンコーディングされたアクションとスケールを合わせるため、0~1で正規化します。
9.Reanalyze
学習に使うサンプルですが、古いパラメータで学習されたサンプルが混じっています。
そこで、学習に使う前に再度最新のネットワークでMCTSを実施し、教師データの $\pi$ と $z$ を更新してから学習する手法がReanalyzeです。
これにより過去のサンプルを使いまわせるのでサンプル効率が上昇します。
ただ、フレームワーク上は実装が複雑になる点とTrainer側でMCTSを実行する必要がある点より実装は見送っています。
10.学習率
論文には書かれていないですが、疑似コードを見るとAlphaZeroから変更があるようです。
AlphaZeroでは固定値を用いて段階的に変更していました(囲碁なら0、30万、50万ステップ後にそれぞれ0.02、0.002、0.0002)が、MuZeroでは指数関数的減衰(wikipedia)な学習率のスケジューリングになっているようです。
$$
\alpha = \alpha_{init} \lambda^{T/ \alpha_t}
$$
$\alpha$ が学習率、$\alpha_{init}$が初期学習率、$\lambda$が減衰率、$T$が総ステップ数、$\alpha_t$が減衰総ステップ数です。
記号と用語は適当なため、コードでも書いておきます
lr_init = 0.05 # 初期学習率
lr_decay_rate = 0.1 # 減衰率
lr_decay_steps = 350e3 # 減衰総ステップ数
T = 総ステップ数
lr = lr_init * lr_decay_rate ** (T / lr_decay_steps)
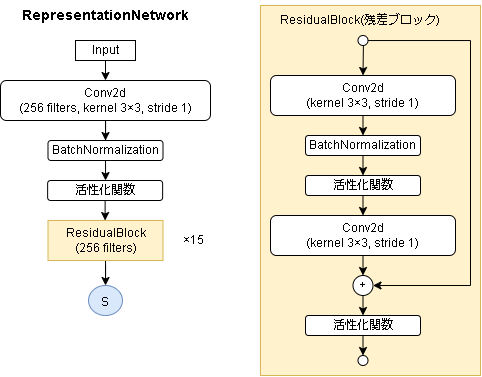
4.ネットワークの構造
基本はAlphaZeroと同じです。
見ると分かりますが中身はほぼResNetです、ので状態が画像っぽい特徴を持っている環境に強そうです。
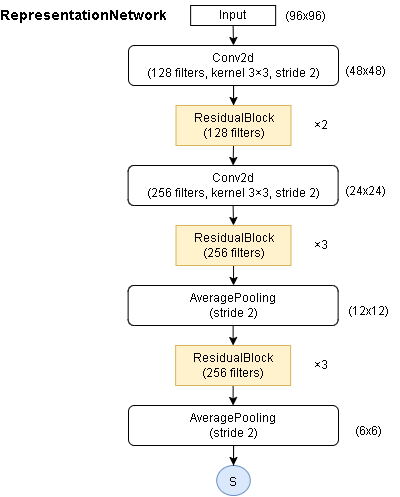
- 表現ネットワーク(ボードゲーム環境)
- 表現ネットワーク(Atari環境)
96x96→6x6のサイズまでダウンサンプリングするようです。(残差ブロックは同じもの)
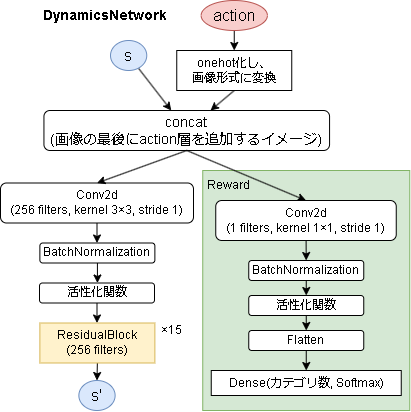
- ダイナミクスネットワーク
AlphaZeroと同じとしか書かれていないのでちょっと自信がないです。
Rewardの出力ですが、最初はResBlockの下に追加していましたが、それだとlossが発散して学習がうまくいきませんでした。
なので図のように直接つなげています。
こうすると、次の状態の予測が表現ネットワークと同じ構造、Rewardの予測はPolicy/Valueと同じ構造になるので多分合っているような気がします。
※ボードゲーム環境は Reward の出力がなくなります。
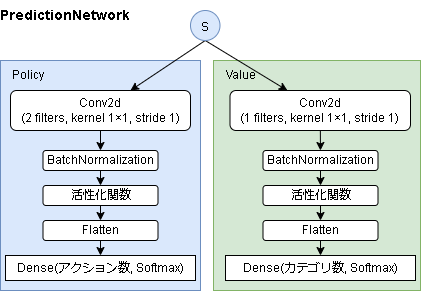
- 予測ネットワーク
※ボードゲーム環境は Value 側の出力は tanh になります。
実装
関係ある個所を抜粋して書いています。
フレームワーク上の実装はgithubを見てください。
Config
ハイパーパラメータです。
値はAtari環境のパラメータにしています。
@dataclass
class Config(DiscreteActionConfig):
num_simulations: int = 50
batch_size: int = 1024
discount: float = 0.997
# 学習率
lr_init: float = 0.05
lr_decay_rate: float = 0.1
lr_decay_steps: int = 350_000
# カテゴリ化する範囲
v_min: int = -300
v_max: int = 300
# policyの温度パラメータのリスト
policy_tau_schedule: List[dict] = [
{"step": 0, "tau": 1.0},
{"step": 500_000, "tau": 0.5},
{"step": 750_000, "tau": 0.25},
]
# td_steps: int = 10 # multisteps
unroll_steps: int = 5 # unroll_steps
# Root prior exploration noise.
root_dirichlet_alpha: float = 0.3
root_exploration_fraction: float = 0.25
# PUCT
c_base: float = 19652
c_init: float = 1.25
# Priority Experience Replay
capacity: int = 1_000_000
memory_name: str = "ProportionalMemory"
memory_warmup_size: int = 1000
memory_alpha: float = 1.0
memory_beta_initial: float = 1.0
memory_beta_steps: int = 1
Network
Atari環境(加工後の 96,96 のグレー画像)を入力した場合を書きます。
各レイヤーの細かい引数は省略しています。(詳細はgitのコードを見てください)
# 残差ブロック(AlphaZeroと同じ)
class _ResidualBlock(keras.Model):
def __init__(self, filters):
super().__init__()
self.conv1 = kl.Conv2D(filters=filters, kernel_size=(3,3))
self.bn1 = kl.BatchNormalization()
self.relu1 = kl.LeakyReLU()
self.conv2 = kl.Conv2D(filters=filters, kernel_size=(3,3))
self.bn2 = kl.BatchNormalization()
self.relu2 = kl.LeakyReLU()
def call(self, x):
x1 = self.conv1(x)
x1 = self.bn1(x1)
x1 = self.relu1(x1)
x1 = self.conv2(x1)
x1 = self.bn2(x1)
x = x + x1
x = self.relu2(x)
return x
# --- 表現ネットワーク
class _RepresentationNetwork(keras.Model):
def __init__(self, config: Config):
super().__init__()
input_shape = (96, 96) # atari image
in_layer = c = kl.Input(shape=input_shape)
c = kl.Reshape(input_shape + (1,))(c) # (w, h) -> (w, h, 1)
# ダウンサンプリング
c = kl.Conv2D(128, kernel_size=3, strides=2, activation="relu")
c = _ResidualBlock(128)(c)
c = _ResidualBlock(128)(c)
c = kl.Conv2D(256, kernel_size=3, strides=2, activation="relu")
c = _ResidualBlock(256)(c)
c = _ResidualBlock(256)(c)
c = _ResidualBlock(256)(c)
c = kl.AveragePooling2D(pool_size=3, strides=2)(c)
c = _ResidualBlock(256)(c)
c = _ResidualBlock(256)(c)
c = _ResidualBlock(256)(c)
c = kl.AveragePooling2D(pool_size=3, strides=2)(c)
self.model = keras.Model(in_state, c)
def call(self, state):
x = self.model(state)
# 隠れ状態はアクションとスケールを合わせるため0-1で正規化(一応batch毎)
batch, h, w, d = x.shape
s_min = tf.reduce_min(tf.reshape(x, (batch, -1)), axis=1, keepdims=True)
s_max = tf.reduce_max(tf.reshape(x, (batch, -1)), axis=1, keepdims=True)
s_min = s_min * tf.ones((batch, h * w * d), dtype=tf.float32)
s_max = s_max * tf.ones((batch, h * w * d), dtype=tf.float32)
s_min = tf.reshape(s_min, (batch, h, w, d))
s_max = tf.reshape(s_max, (batch, h, w, d))
epsilon = 1e-4 # div0 回避
x = (x - s_min + epsilon) / tf.maximum((s_max - s_min), 2 * epsilon)
return x
# --- ダイナミクスネットワーク
class _DynamicsNetwork(keras.Model):
def __init__(self, config: Config, input_shape):
super().__init__()
self.action_num = config.action_num
v_num = config.v_max - config.v_min + 1
# input_shapeは表現ネットワーク後のshapeなので(6, 6, 256)
h, w, ch = input_shape
# hidden_state + action_space
in_state = c = kl.Input(shape=(h, w, ch + self.action_num))
# AlphaZeroブロック(詳細はAlphaZeroの記事を参照)
c1 = AlphaZeroImageBlock(n_blocks=15)(c)
# reward
c2 = kl.Conv2D(1, kernel_size=1)(c)
c2 = kl.BatchNormalization()(c2)
c2 = kl.LeakyReLU()(c2)
c2 = kl.Flatten()(c2)
reward = kl.Dense(v_num, activation="softmax")(c2)
# 出力は hidden_state, reward(category)
self.model = keras.Model(in_state, [c1, reward])
def call(self, hidden_state, action):
batch_size, h, w, _ = hidden_state.shape
# --- actionをイメージ化する
action_image = tf.one_hot(action, self.action_num) # (batch, action)
action_image = tf.repeat(action_image, repeats=h * w, axis=1) # (batch, action * h * w)
action_image = tf.reshape(action_image, (batch_size, self.action_num, h, w)) # (batch, action, h, w)
action_image = tf.transpose(action_image, perm=[0, 2, 3, 1]) # (batch, h, w, action)
# --- hidden_stateの最後にアクション層を追加
in_state = tf.concat([hidden_state, action_image], axis=3)
x, reward_category = self.model(in_state)
# 隠れ状態はアクションとスケールを合わせるため0-1で正規化(一応batch毎)
batch, h, w, d = x.shape
s_min = tf.reduce_min(tf.reshape(x, (batch, -1)), axis=1, keepdims=True)
s_max = tf.reduce_max(tf.reshape(x, (batch, -1)), axis=1, keepdims=True)
s_min = s_min * tf.ones((batch, h * w * d), dtype=tf.float32)
s_max = s_max * tf.ones((batch, h * w * d), dtype=tf.float32)
s_min = tf.reshape(s_min, (batch, h, w, d))
s_max = tf.reshape(s_max, (batch, h, w, d))
epsilon = 1e-4 # div0 回避
x = (x - s_min + epsilon) / tf.maximum((s_max - s_min), 2 * epsilon)
return x, reward_category
# --- 予測ネットワーク
class _PredictionNetwork(keras.Model):
def __init__(self, config: Config, input_shape):
super().__init__()
v_num = config.v_max - config.v_min + 1
# input_shapeは表現ネットワーク後のshapeなので(6, 6, 256)
in_layer = c = kl.Input(shape=input_shape)
# --- policy
c1 = kl.Conv2D(2, kernel_size=(1, 1))(c)
c1 = kl.BatchNormalization()(c1)
c1 = kl.LeakyReLU()(c1)
c1 = kl.Flatten()(c1)
policy = kl.Dense(config.action_num, activation="softmax")(c1)
# --- value
c2 = kl.Conv2D(1, kernel_size=(1, 1))(c)
c2 = kl.BatchNormalization()(c2)
c2 = kl.LeakyReLU()(c2)
c2 = kl.Flatten()(c2)
value = kl.Dense(v_num, activation="softmax")(c2)
self.model = keras.Model(in_layer, [policy, value])
def call(self, state):
return self.model(state)
Parameter
AlphaZeroとほぼ同じなのでコードは省略します。
追加として、MCTS時のQ値正規化で使うQ値の最大値と最小値を保存しています。
RemoteMemory
Rainbowの Prioritized Experience Replayで実装したものをそのまま使っています。
コードは省略。
カテゴリ化用の関数
def float_category_encode(val: float, v_min: int, v_max: int) -> List[float]:
category = [0.0 for _ in range(v_max - v_min + 1)]
low_int = math.floor(val)
high_int = low_int + 1
weight = val - low_int
category[int(low_int - v_min)] = 1 - weight
category[int(high_int - v_min)] = weight
return category
def float_category_decode(category: List[float], v_min: int) -> float:
n = 0
for i, w in enumerate(category):
n += (i + v_min) * w
return n
Worker
流れはAlphaZeroと同じですが、細かいところが変わっています。
class Worker(DiscreteActionWorker):
def __init__(self, *args):
super().__init__(*args)
# 温度パラメータを扱いやすいように変更
self.policy_tau_schedule = {}
for tau_list in self.config.policy_tau_schedule:
self.policy_tau_schedule[tau_list["step"]] = tau_list["tau"]
self.policy_tau = self.policy_tau_schedule[0]
self.total_step = 0
def call_on_reset(self, state: np.ndarray, invalid_actions: List[int]) -> None:
self.step = 0
self.history = []
self.N = {} # 訪問回数(s,a)
self.W = {} # 累計報酬(s,a)
self.Q = {}
def _init_state(self, state_str):
if state_str not in self.N:
self.N[state_str] = [0 for _ in range(self.config.action_num)]
self.W[state_str] = [0 for _ in range(self.config.action_num)]
self.Q[state_str] = [0 for _ in range(self.config.action_num)]
def call_policy(self, state: np.ndarray, invalid_actions: List[int]) -> int:
# --- 表現ネットワークから初期状態を取得
s0 = self.parameter.representation_network(state[np.newaxis, ...])
s0_str = s0.ref()
# --- シミュレーション
for _ in range(self.config.num_simulations):
self._simulation(s0, s0_str, invalid_actions)
# --- 確率に比例したアクションを選択
if not self.training:
self.policy_tau = 0 # 評価時は決定的に
if self.policy_tau == 0:
# 温度パラメータ0は決定的
counts = np.asarray(self.N[s0_str])
action = random.choice(np.where(counts == counts.max())[0])
else:
# 確率的
step_policy = np.array(
[self.N[s0_str][a] ** (1 / policy_tau) for a in range(self.config.action_num)]
)
step_policy /= step_policy.sum()
action = random_choice_by_probs(step_policy)
# 温度パラメータのschedule check
if self.total_step in self.policy_tau_schedule:
self.policy_tau = self.policy_tau_schedule[self.total_step]
# 学習用のpolicyはtau=1
N = sum(self.N[self.s0_str])
self.step_policy = [self.N[self.s0_str][a] / N for a in range(self.config.action_num)]
# サンプル用に保存
self.state = state
self.action = int(action)
self.state_v = self.parameter.V[s0_str]
return self.action
# --- シミュレーション(1step,再帰,次の報酬を返す)
def _simulation(self, state, state_str, invalid_actions, depth: int = 0):
if depth >= 99999: # for safety
return 0
# PVを予測
self._init_state(state_str)
self.parameter.pred_PV(state, state_str)
# actionを選択
puct_list = self._calc_puct(state_str, invalid_actions, depth == 0)
action = random.choice(np.where(puct_list == np.max(puct_list))[0])
# 次の状態を取得
n_state, reward_category = self.parameter.dynamics_network(state, [action])
n_state_str = n_state.ref()
reward = float_category_decode(reward_category.numpy()[0], self.config.v_min)
enemy_turn = self.config.env_player_num > 1 # 2player以上は相手番と決め打ち
if self.N[state_str][action] == 0:
# leaf node ならロールアウト
self.parameter.pred_PV(n_state, n_state_str)
n_reward = self.parameter.V[n_state_str]
else:
# 子ノードに降りる(展開)
n_reward = self._simulation(n_state, n_state_str, [], depth + 1)
# 次が相手のターンなら、報酬は最小になってほしいので-をかける
if enemy_turn:
n_reward = -n_reward
# 割引報酬
reward = reward + self.config.discount * n_reward
self.N[state_str][action] += 1
self.W[state_str][action] += reward
self.Q[state_str][action] = self.W[state_str][action] / self.N[state_str][action]
self.parameter.q_min = min(self.parameter.q_min, self.Q[state_str][action])
self.parameter.q_max = max(self.parameter.q_max, self.Q[state_str][action])
return reward
def _calc_puct(self, state_str, invalid_actions, is_root):
AlphaZeroとほぼ同じなので省略。
追加要素は、Q値の正規化(MinMax)だけです。
def call_on_step(
self,
next_state: np.ndarray,
reward: float,
done: bool,
next_invalid_actions: List[int],
):
self.step += 1
self.total_step += 1
if not self.training:
return {}
self.history.append(
{
"state": self.state,
"action": self.action,
"policy": self.step_policy,
"reward": reward,
"state_v": self.state_v,
}
)
# 終了時に割引報酬を計算してサンプルを送る
if done:
zero_category = float_category_encode(0, self.config.v_min, self.config.v_max)
# calc MC reward
reward = 0
for h in reversed(self.history):
reward = h["reward"] + self.config.discount * reward
h["discount_reward"] = reward
# batch create
for idx in range(len(self.history)):
# --- policies
policies = [
[1 / self.config.action_num] * self.config.action_num for _ in range(self.config.unroll_steps + 1)
]
for i in range(self.config.unroll_steps + 1):
if idx + i >= len(self.history):
break
policies[i] = self.history[idx + i]["policy"]
# --- values
values = [zero_category for _ in range(self.config.unroll_steps + 1)]
priority = 0
for i in range(self.config.unroll_steps + 1):
if idx + i >= len(self.history):
break
v = self.history[idx + i]["discount_reward"]
v = rescaling(v)
priority += v - self.history[idx + i]["state_v"]
values[i] = float_category_encode(v, self.config.v_min, self.config.v_max)
priority /= self.config.unroll_steps + 1
# --- actions
actions = [random.randint(0, self.config.action_num - 1) for _ in range(self.config.unroll_steps)]
for i in range(self.config.unroll_steps):
if idx + i >= len(self.history):
break
actions[i] = self.history[idx + i]["action"]
# --- rewards
rewards = [zero_category for _ in range(self.config.unroll_steps)]
for i in range(self.config.unroll_steps):
if idx + i >= len(self.history):
break
r = self.history[idx + i]["reward"]
r = rescaling(r)
rewards[i] = float_category_encode(r, self.config.v_min, self.config.v_max)
self.remote_memory.add(
{
"state": self.history[idx]["state"],
"actions": actions,
"policies": policies,
"values": values,
"rewards": rewards,
},
priority,
)
return {}
Trainer
学習部分です。
3つのネットワークを同時に学習させます。
def _scale_gradient(tensor, scale):
""" Scales the gradient for the backward pass. """
return tensor * scale + tf.stop_gradient(tensor) * (1 - scale)
class Trainer(RLTrainer):
def __init__(self, *args):
super().__init__(*args)
self.optimizer = keras.optimizers.Adam()
# バッチ毎に出力
self.cross_entropy_loss = keras.losses.CategoricalCrossentropy(axis=1, reduction=keras.losses.Reduction.NONE)
self.train_count = 0
def train(self):
if self.remote_memory.length() < self.config.memory_warmup_size:
return {}
indices, batchs, weights = self.remote_memory.sample(self.train_count, self.config.batch_size)
# (batch, dict, val) -> (batch, val)
states = batchsよりデータ変換
# (batch, dict, steps, val) -> (steps, batch, val)
actions_list = batchsよりデータ変換
policies_list = batchsよりデータ変換
values_list = batchsよりデータ変換
rewards_list = batchsよりデータ変換
with tf.GradientTape() as tape:
# --- 1st step
hidden_states = self.parameter.representation_network(states)
p_pred, v_pred = self.parameter.prediction_network(hidden_states)
# loss
policy_loss = _scale_gradient(self.cross_entropy_loss(policies_list[0], p_pred), 1.0)
value_loss = _scale_gradient(self.cross_entropy_loss(values_list[0], v_pred), 1.0)
reward_loss = tf.constant([0] * self.config.batch_size, dtype=tf.float32)
# --- unroll steps
gradient_scale = 1 / self.config.unroll_steps
for t in range(self.config.unroll_steps):
# pred
n_hidden_states, p_rewards = self.parameter.dynamics_network(hidden_states, actions_list[t])
p_pred, v_pred = self.parameter.prediction_network(hidden_states)
# loss
value_loss += _scale_gradient(self.cross_entropy_loss(values_list[t + 1], v_pred), gradient_scale)
policy_loss += _scale_gradient(self.cross_entropy_loss(policies_list[t + 1], p_pred), gradient_scale)
reward_loss += _scale_gradient(self.cross_entropy_loss(rewards_list[t], p_rewards), gradient_scale)
hidden_states = _scale_gradient(n_hidden_states, 0.5)
loss = tf.reduce_mean((value_loss + policy_loss + reward_loss) * weights)
# 各ネットワークの正則化項を加える
loss += tf.reduce_sum(self.parameter.representation_network.losses)
loss += tf.reduce_sum(self.parameter.prediction_network.losses)
loss += tf.reduce_sum(self.parameter.dynamics_network.losses)
priorities = value_loss.numpy()
# lr
lr = self.config.lr_init * self.config.lr_decay_rate ** (self.train_count / self.config.lr_decay_steps)
self.optimizer.learning_rate = lr
variables = [
self.parameter.representation_network.trainable_variables,
self.parameter.prediction_network.trainable_variables,
self.parameter.dynamics_network.trainable_variables,
]
grads = tape.gradient(loss, variables)
for i in range(len(variables)):
self.optimizer.apply_gradients(zip(grads[i], variables[i]))
self.train_count += 1
# memory update
self.remote_memory.update(indices, batchs, priorities)
# 学習したらキャッシュは削除
self.parameter.reset_cache()
return {}
学習
学習ですが、ちょっとスペック不足で良い結果は得られていません。
(記事を作った後ここだけでずっと止まっていたのであきらめて投稿優先にしました)
メンダコさんのブログではGCPの24-vCPU/128GB RAM/GPU T4 にて48時間学習させてやっと学習され始めた感じでした。
環境も込みで学習させるのはかなり大変な印象です…
一応すごく簡単な環境で学習できていそうなことは確認しています。
確認に使ったコードは github を参照してください。
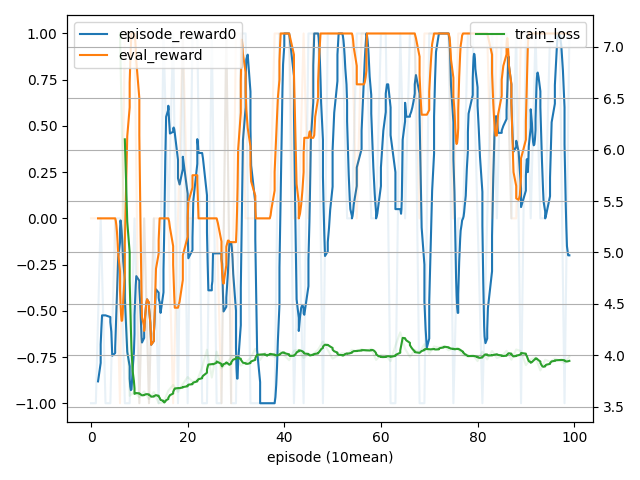
- 学習過程
- 最終結果
詳細
mean 0.9
### env: EasyGrid, rl: MuZero, max episodes: 1, timeout: -1.00s, max steps: -1, max train: -1
### 0, action 1, rewards [0.], next 0
env None
work0 None
......
. G.
. . X.
.P .
......
V_net: 0.00093
← : 30.0% ( 3)(N), -0.04073(Q), 0.82048(PUCT), 0.26116(P), 0.01713(V), -0.00000(reward)
*↓ : 30.0% ( 3)(N), -0.00512(Q), 0.82438(PUCT), 0.25196(P), -0.02588(V), -0.00000(reward)
→ : 20.0% ( 2)(N), -0.10464(Q), 0.83826(PUCT), 0.22702(P), -0.05165(V), 0.00002(reward)
↑ : 20.0% ( 2)(N), 0.01738(Q), 0.92602(PUCT), 0.25986(P), 0.10656(V), -0.00000(reward)
### 1, action 2, rewards [0.], next 0
env {}
work0 {}
......
. G.
. . X.
.P .
......
V_net: 0.00093
← : 10.0% ( 1)(N), 0.01542(Q), 1.09914(PUCT), 0.26116(P), 0.01713(V), -0.00000(reward)
↓ : 30.0% ( 3)(N), 0.03892(Q), 0.84043(PUCT), 0.25196(P), -0.02588(V), -0.00000(reward)
*→ : 30.0% ( 3)(N), -0.06568(Q), 0.77764(PUCT), 0.22702(P), -0.05165(V), 0.00002(reward)
↑ : 30.0% ( 3)(N), 0.09346(Q), 0.86812(PUCT), 0.25986(P), 0.10656(V), -0.00000(reward)
### 2, action 0, rewards [0.], next 0
env {}
work0 {}
......
. G.
. . X.
. P .
......
V_net: -0.04048
*← : 30.0% ( 3)(N), -0.08089(Q), 0.81989(PUCT), 0.27536(P), -0.03399(V), -0.00000(reward)
↓ : 30.0% ( 3)(N), -0.13046(Q), 0.76042(PUCT), 0.23349(P), -0.05853(V), -0.00000(reward)
→ : 20.0% ( 2)(N), 0.14803(Q), 0.92660(PUCT), 0.22417(P), -0.09467(V), -0.00001(reward)
↑ : 20.0% ( 2)(N), 0.01059(Q), 0.93294(PUCT), 0.26698(P), 0.01991(V), -0.00000(reward)
### 3, action 0, rewards [0.], next 0
env {}
work0 {}
......
. G.
. . X.
.P .
......
V_net: 0.00093
*← : 30.0% ( 3)(N), 0.04557(Q), 0.85194(PUCT), 0.26116(P), 0.01713(V), -0.00000(reward)
↓ : 20.0% ( 2)(N), -0.07088(Q), 0.88344(PUCT), 0.25196(P), -0.02588(V), -0.00000(reward)
→ : 20.0% ( 2)(N), 0.08817(Q), 0.90854(PUCT), 0.22702(P), -0.05165(V), 0.00002(reward)
↑ : 30.0% ( 3)(N), 0.06965(Q), 0.85944(PUCT), 0.25986(P), 0.10656(V), -0.00000(reward)
### 4, action 2, rewards [0.], next 0
env {}
work0 {}
......
. G.
. . X.
.P .
......
V_net: 0.00093
← : 20.0% ( 2)(N), 0.00721(Q), 0.92403(PUCT), 0.26116(P), 0.01713(V), -0.00000(reward)
↓ : 30.0% ( 3)(N), 0.03468(Q), 0.83888(PUCT), 0.25196(P), -0.02588(V), -0.00000(reward)
*→ : 30.0% ( 3)(N), 0.06285(Q), 0.82450(PUCT), 0.22702(P), -0.05165(V), 0.00002(reward)
↑ : 20.0% ( 2)(N), 0.01738(Q), 0.92602(PUCT), 0.25986(P), 0.10656(V), -0.00000(reward)
### 5, action 2, rewards [0.], next 0
env {}
work0 {}
......
. G.
. . X.
. P .
......
V_net: -0.04048
← : 20.0% ( 2)(N), -0.10761(Q), 0.90089(PUCT), 0.27536(P), -0.03399(V), -0.00000(reward)
↓ : 20.0% ( 2)(N), -0.10087(Q), 0.84816(PUCT), 0.23349(P), -0.05853(V), -0.00000(reward)
*→ : 30.0% ( 3)(N), 0.22578(Q), 0.88106(PUCT), 0.22417(P), -0.09467(V), -0.00001(reward)
↑ : 30.0% ( 3)(N), 0.03407(Q), 0.85351(PUCT), 0.26698(P), 0.01991(V), -0.00000(reward)
### 6, action 3, rewards [0.], next 0
env {}
work0 {}
......
. G.
. . X.
. P .
......
V_net: -0.17732
← : 30.0% ( 3)(N), -0.03739(Q), 0.87928(PUCT), 0.31939(P), 0.01362(V), -0.00000(reward)
↓ : 20.0% ( 2)(N), -0.23994(Q), 0.83116(PUCT), 0.25905(P), -0.27282(V), -0.00000(reward)
→ : 20.0% ( 2)(N), -0.22467(Q), 0.73084(PUCT), 0.17873(P), -0.57103(V), 0.00122(reward)
*↑ : 30.0% ( 3)(N), -0.03532(Q), 0.80433(PUCT), 0.24282(P), -0.13405(V), 0.00000(reward)
### 7, action 3, rewards [0.], next 0
env {}
work0 {}
......
. G.
. .PX.
. .
......
V_net: -0.20280
← : 10.0% ( 1)(N), -0.34660(Q), 0.93957(PUCT), 0.24719(P), -0.38495(V), -0.00014(reward)
↓ : 30.0% ( 3)(N), -0.15365(Q), 0.79115(PUCT), 0.27312(P), -0.29529(V), -0.00008(reward)
→ : 20.0% ( 2)(N), -0.93884(Q), 0.47899(PUCT), 0.18516(P), -0.00002(V), -0.95263(reward)
*↑ : 40.0% ( 4)(N), 0.10197(Q), 0.84726(PUCT), 0.29453(P), 0.61191(V), -0.05256(reward)
### 8, action 2, rewards [0.], next 0
env {}
work0 {}
......
. PG.
. . X.
. .
......
V_net: 0.47785
← : 20.0% ( 2)(N), 0.18462(Q), 0.90557(PUCT), 0.19810(P), 0.42803(V), -0.00000(reward)
↓ : 10.0% ( 1)(N), -0.05041(Q), 0.89258(PUCT), 0.16882(P), -0.05601(V), -0.00000(reward)
*→ : 60.0% ( 6)(N), 1.10881(Q), 1.23102(PUCT), 0.44197(P), 0.00763(V), 0.99182(reward)
↑ : 10.0% ( 1)(N), 0.35312(Q), 1.08373(PUCT), 0.19110(P), 0.37839(V), 0.01257(reward)
### 9, action 2, rewards [1.], done(env), next 0
env {}
work0 {}
......
. P.
. . X.
. .
......
rewardはちゃんと学習されています。
lossがまだ安定していないのでこれでもまだ学習が足りていなそうです…。
MuZeroの問題点
論文でも触れられている課題ですが、ダイナミクスネットワークは次の状態への遷移が決定的です。
マルコフ決定過程は確率的なのでこれは正確ではありません。
これを解決したのが次の手法である Stochastic MuZero です。