【強化学習】MuZeroを完成させたStochasticMuZeroを解説・実装

この記事は自作している強化学習フレームワーク SimpleDistributedRL の解説記事です。

前：MuZero

Stochastic MuZero

Stochasticはストキャスティック(stəkǽstik)と読み、"確率論的な"という意味です。

MuZeroは次の状態が決定的でないと学習できないという問題がありました。
マルコフ決定過程(MDP)の環境では次の状態が確率論的に決まる環境を想定しているため、適用できる環境が限定的です。
Stochastic MuZero は次の状態を確率的に予測できるようにしたMuZeroとなります。

参考
・Planning in Stochastic Environments with a Learned Model (論文)

事後状態（Afterstates）

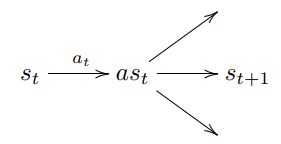
今の状態と次の状態の間に事後状態という概念を追加します。

今の状態 $s_t$ から アクション $a_t$ を実行した後、事後状態 $as_t$ に一度遷移し、その後次の状態 $s_{t+1}$ に遷移します。
これにより、アクションによる環境への影響と、その後に変化する環境の状態を分離します。

chance outcomes（遷移候補と結果）

意味する所は、事後状態から次の状態の候補が"chance"で、実際に観測された次の状態が"outcomes"です。
Stochastic MuZeroではこれをVQ-VAEを用いて表現します。

VQ-VAE

データの特徴を獲得するニューラルネットワークの１つにVAEというものがあります。
VAEは特徴量が連続値で表現されますが、これを離散値で表現できるようにしたのがVQ-VAEです。
VQ-VAEについては参考記事を見てください。（詳細は割愛します）

参考
・【論文解説+Tensorflowで実装】VQ-VAEを理解する
・Neural Discrete Representation Learning(論文)

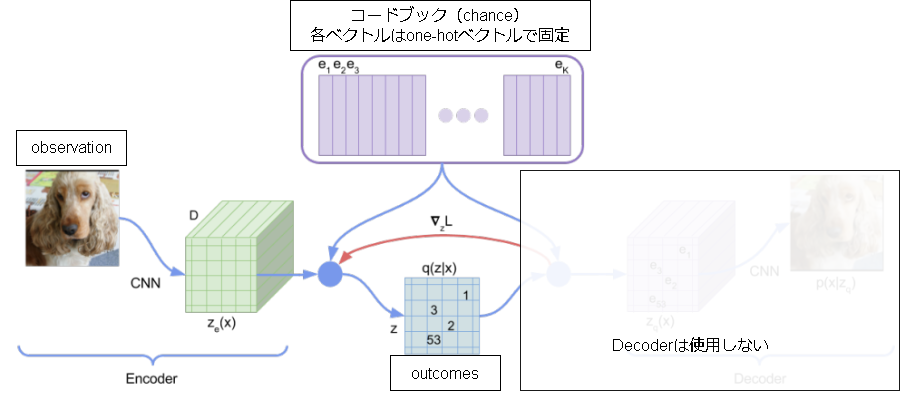
Stochastic MuZero では以下のように適用します。(VQ-VAE側の論文の図を元に追記)

コードブックが"chance"を表し、Encodeの結果出力される潜在変数 z が"outcomes"になります。
コードブックは固定のone-hotベクトルで表し、コードブック側の学習を不要にして簡略化しています。（実際のVQ-VAEではコードブック側も学習する）
Encoderの学習はMuZeroと同じく他のネットワークも含めて学習させるため、Decoderは不要となります。

Stochastic MuZero のモデル

MuZeroでは3つのモデルが使われていましたが、Stochastic MuZero では更に3つ追加した計6つのモデルが使われます。
追加されたモデルは以下です。

• Afterstate Dynamics
  表現ネットワークでエンコードされた状態とアクションから、事後状態を予測するモデル

• Afterstate Prediction
  事後状態から、Q値と"chance outcomes"を予測するモデル

• VQ-VAE(encoder)
  状態から、"chance outcomes" を出力するモデル

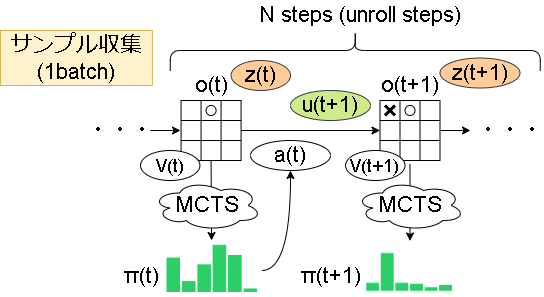
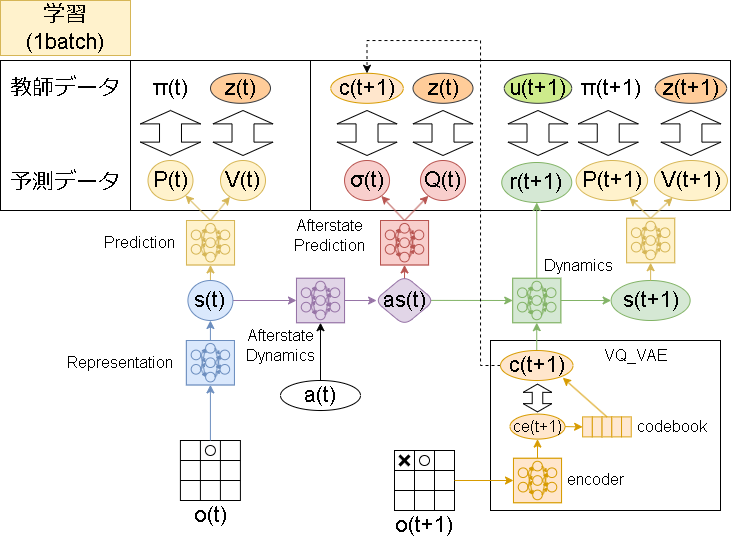
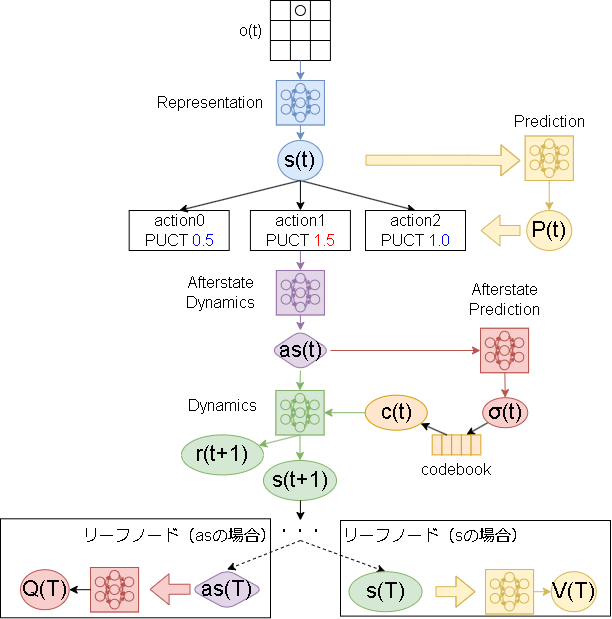
全体像は以下です。（サンプル収集はMuZeroと変わりません）

学習がだいぶ複雑になりましたね…。ただ複雑ですが難しい点はないかと思います。

損失

大きくMuZero側とchance側があります。

$$
L^{total} = L^{MuZero} + L^{chance}
$$

MuZero側は変更なく以下です。

$$
L^{MuZero} = \sum_{k=0}^K{ l^p(\pi_{t+k}, p_t^k)} + \sum_{k=0}^K{ l^v(z_{t+k}, v_t^k) } + \sum_{k=1}^K{ l^r(u_{t+k}, r_t^k) }
$$

chance側は以下です。

L^{chance}_w = \sum_{k=0}^{K-1}{l^Q(z_{t+k}, Q_t^k)} + \sum_{k=0}^{K-1}{l^{\sigma}(c_{t+k+1}, \sigma_t^k) } + \beta \sum_{k=0}^{K-1}|| c_{t+k+1} - c^e_{t+k+1} ||^2

MuZeroと同様にボードゲーム環境（碁とバックギャモン）とMDP環境（2048ゲーム）で微妙に違いがあります。

環境	ボードゲーム	MDP
$l^p$	cross entropy loss	cross entropy loss
$l^v$	MSE	cross entropy loss(※1)
$l^r$	MSE	cross entropy loss(※1)
$l^Q$	MSE	cross entropy loss(※1)
$l^{\sigma}$	cross entropy loss	cross entropy loss

(※1)はMuzeroと同じで rescaling 関数を適用した後にカテゴリ化します。

また、最後の項は VQ-VAE の commitment cost というものを表しており、エンコードの出力をコードブックに近づける項となります。
（ただ論文では数式に記載はありますが、疑似コードにはここの損失にあたるコードがなかったり…）

MCTS

Stochastic MuZero の MCTS は以下です。

基本はMuZeroと同じで異なる部分は以下です。

• 各ノードですが、状態（s）だけではなく事後状態（as）も１つのノードと見て木構造を作成します。
  リーフノードが s の場合は Prediction から予測された V がロールアウトの価値として使われ、リーフノードが as の場合は AfterstatePrediction から予測された Q がロールアウトの価値として使われます。
• Afterstate Prediction から出力された遷移候補(σ)から遷移結果(c)を求め、Dynamicsの入力とします。
  Dynamicsは as と c を使って次の状態（と即時報酬）を返します。

モデル

論文内では一般的な話は出てこず、実験で使用した内容しか書かれていませんでした。
2048ゲームでは、DynamicsNetwork, AfterstateDynamicsNetwork, VQ_VAE を残差ブロック(ResNet v2)×10とLayerNormalization層とRelu層（各層は256サイズ）で表したそうです。

MuZeroからの流れを考えると、各モデルは以下だと思います。

モデル	Layersイメージ
RepresentationNetwork	EnvState -> (ResNet) -> s
PredictionNetwork	s -> (Conv2d) -> [P, V]
AfterstateDynamicsNetwork	[s,action] -> (ResNet) -> as
AfterstatePredictionNetwork	as -> (Conv2d) -> [code, Q]
DynamicsNetwork(next state)	[as,code] -> (ResNet) -> s
DynamicsNetwork(reward)	[as,code] -> (Conv2d) -> reward
VQ_VAE	EnvState -> (ResNet) -> (Conv2d) -> code

(ResNet)は残差ブロックを重ねた層です。
(Conv2d)は "Conv2D -> BN -> ReLU -> Flatten -> Dense" による表現の集約と値の出力層です。

その他の話

勾配のスケーリング

MuZeroであった勾配のスケーリングが疑似コードからなくなっていました。
（展開ステップでも状態を入力しているから？）

ディリクレノイズの調整

探索のために導入しているディリクレノイズですが、バックギャモンでは有効なアクションの変化が激しいので $\alpha$ を以下のように動的に変化させて対応しているようです。（碁、2048では実施せず 0.3で固定）

$$ \alpha = \frac{1}{\sqrt{有効なアクション数}}$$

実装

基本は MuZero と同じなので差異のある箇所を書いていきます。
フレームワーク上の実装はgithubを見てください。

ハイパーパラメータ

MuZeroから追加された大きいパラメータはコードブックのサイズぐらいでしょうか。

codebook_size: int = 32

root_dirichlet_alpha: float = 0.3
root_dirichlet_fraction: float = 0.1
root_dirichlet_adaptive: bool = False  # ディリクレノイズの調整をするか

commitment_cost: float = 0.25  # VQ-VAEのβ

モデル

MuZeroと同じく、Atari環境(加工後の (96,96) のグレー画像)を入力した場合を書きます。
各レイヤーの細かい引数は省略しています。(詳細はgitのコードを見てください)

また、今までと異なり論文内で正則化層と活性化関数が LayerNormalization と ReLU と明記されています。
ただ、値を出力する層で LayerNormalization は効果が薄いというか学習できない（直前のLayer数が1か2）のでそこは BatchNormalization を使用しています。

class _RepresentationNetwork(keras.Model):
    表現ネットワームはMuZeroと同じなので省略

# --- ダイナミクスネットワーク
# 入力がアクション→コードブックに変わっています
class _DynamicsNetwork(keras.Model):
    def __init__(self, config: Config, as_shape):
        super().__init__()
        self.c_size = config.codebook_size
        v_num = config.v_max - config.v_min + 1

        # as_shapeはafterstateでAtariだと(6, 6, 256)
        h, w, ch = as_shape

        # as_shape + code_shape
        in_state = c = kl.Input(shape=(h, w, ch + self.c_size))

        # AlphaZeroブロック(詳細はAlphaZeroの記事を参照)
        c1 = AlphaZeroImageBlock(n_blocks=10, filters=ch)(c)

        # reward
        c2 = kl.Conv2D(1, kernel_size=1)(c)
        c2 = kl.BatchNormalization()(c2)
        c2 = kl.ReLU()(c2)
        c2 = kl.Flatten()(c2)
        reward = kl.Dense(v_num, activation="softmax")(c2)

        self.model = keras.Model(in_state, [c1, reward])

    def call(self, as_state, code_state):
        batch, h, w, _ = as_state.shape

        # --- code_stateをイメージ化する(code_stateはone-hotされている)
        code_image = tf.repeat(code_state, h * w, axis=1)  # (b, c_size)->(b, c_size * h * w)
        code_image = tf.reshape(code_image, (batch, self.c_size, h, w))  # (b, c_size * h * w)->(b, c_size, h, w)
        code_image = tf.transpose(code_image, perm=[0, 2, 3, 1])  # (b, c_size, h, w)->(b, h, w, c_size)

        # --- 最後に追加
        in_state = tf.concat([as_state, code_image], axis=3)
        x, reward_category = self.model(in_state)

        # 隠れ状態はアクションとスケールを合わせるため0-1で正規化(一応batch毎)
        batch, h, w, d = x.shape
        s_min = tf.reduce_min(tf.reshape(x, (batch, -1)), axis=1, keepdims=True)
        s_max = tf.reduce_max(tf.reshape(x, (batch, -1)), axis=1, keepdims=True)
        s_min = s_min * tf.ones((batch, h * w * d), dtype=tf.float32)
        s_max = s_max * tf.ones((batch, h * w * d), dtype=tf.float32)
        s_min = tf.reshape(s_min, (batch, h, w, d))
        s_max = tf.reshape(s_max, (batch, h, w, d))
        epsilon = 1e-4  # div0 回避
        x = (x - s_min + epsilon) / tf.maximum((s_max - s_min), 2 * epsilon)

        # 出力は hidden_state, reward(category)
        return x, reward_category


class _PredictionNetwork(keras.Model):
    予測ネットワークはMuZeroと同じなので省略

# --- AfterstateDynamics
class _AfterstateDynamicsNetwork(keras.Model):
    def __init__(self, config: Config, hidden_shape):
        super().__init__()
        self.action_num = config.action_num
        h, w, ch = hidden_shape

        # hidden_state + action_space
        in_state = c = kl.Input(shape=(h, w, ch + self.action_num))

        # AlphaZeroブロック(詳細はAlphaZeroの記事を参照)
        c = AlphaZeroImageBlock(n_blocks=config.dynamics_blocks, filters=ch)(c)

        self.model = keras.Model(in_state, c)

    def call(self, hidden_state, action):
        batch_size, h, w, _ = hidden_state.shape

        # --- actionをイメージ化する
        action_image = tf.one_hot(action, self.action_num)  # (batch, action)
        action_image = tf.repeat(action_image, repeats=h * w, axis=1)  # (batch, action * h * w)
        action_image = tf.reshape(action_image, (batch_size, self.action_num, h, w))  # (batch, action, h, w)
        action_image = tf.transpose(action_image, perm=[0, 2, 3, 1])  # (batch, h, w, action)

        # --- 最後に追加
        in_state = tf.concat([hidden_state, action_image], axis=3)
        return self.model(in_state)

# --- AfterstatePrediction
class _AfterstatePredictionNetwork(keras.Model):
    def __init__(self, config: Config, as_shape):
        super().__init__()

        v_num = config.v_max - config.v_min + 1
        in_layer = c = kl.Input(shape=as_shape)

        # --- code
        c1 = kl.Conv2D(2, kernel_size=(1, 1))(c)
        c1 = kl.BatchNormalization()(c1)
        c1 = kl.ReLU()(c1)
        c1 = kl.Flatten()(c1)
        c1 = kl.Dense(config.codebook_size, activation="softmax")(c1)

        # --- Q
        c2 = kl.Conv2D(1, kernel_size=(1, 1))(c)
        c2 = kl.BatchNormalization()(c2)
        c2 = kl.ReLU()(c2)
        c2 = kl.Flatten()(c2)
        c2 = kl.Dense(v_num, activation="softmax")(c2)

        self.model = keras.Model(in_layer, [c1, c2])

    def call(self, state):
        return self.model(state)

# --- VQ_VAE
class _VQ_VAE(keras.Model):
    def __init__(self, config: Config):
        super().__init__()

        # --- codebook(one-hot vector)
        self.c_size = config.codebook_size
        self.codebook = np.identity(self.c_size, dtype=np.float32)[np.newaxis, ...]

        # --- model(atari input)
        input_shape = (96, 96)
        in_layer = c = kl.Input(shape=input_shape)
        c = kl.Reshape(input_shape + (1,))(c)  # (w, h) -> (w, h, 1)
        c = kl.Conv2D(128, kernel_size=3, strides=2, activation="relu")
        c = _ResidualBlock(128)(c)
        c = _ResidualBlock(128)(c)
        c = kl.Conv2D(256, kernel_size=3, strides=2, activation="relu")
        c = _ResidualBlock(256)(c)
        c = _ResidualBlock(256)(c)
        c = _ResidualBlock(256)(c)
        c = kl.AveragePooling2D(pool_size=3, strides=2)(c)
        c = _ResidualBlock(256)(c)
        c = _ResidualBlock(256)(c)
        c = _ResidualBlock(256)(c)
        c = kl.AveragePooling2D(pool_size=3, strides=2)(c)

        # output
        c = kl.Conv2D(filters=2, kernel_size=(1, 1))(c)
        c = kl.BatchNormalization()(c)
        c = kl.ReLU()(c)
        c = kl.Flatten()(c)
        c = kl.Dense(config.codebook_size, activation="softmax")(c)

        self.model = keras.Model(in_state, c)

    def call(self, state):
        x = self.model(state)
        return self.encode(x), x  # encode前も返す

    def encode(self, x):
        # codebookに一番近いベクトルを返す、とりあえず愚直に実装
        batch = x.shape[0]
        codebook = np.tile(self.codebook, (batch, 1, 1))  # [1, c, c]->[b, c, c]

        x = np.tile(x, (1, self.c_size))  # [b, c]->[b, c*c]
        x = np.reshape(x, (-1, self.c_size, self.c_size))  # [b, c*c]->[b, c, c]

        distance = np.sum((x - codebook) ** 2, axis=2)
        indices = np.argmin(distance, axis=1)
        onehot = np.identity(self.c_size, dtype=np.float32)[indices]
        onehot = np.tile(onehot, (1, self.c_size)).reshape((-1, self.c_size, self.c_size))  # [b, c, c]
        code = np.sum(onehot * codebook, axis=2)  # [b, c, c]->[b, c]

        return code

Parameter

MuZeroとほぼ同じです。
追加は、Predictionの予測値PVだけではなくAfterstatePredictionの予測値QCもキャッシュしている点だけです。

Worker

シミュレーション部分のみ抜粋します。

class Worker(DiscreteActionWorker):
    def call_policy(self, state: np.ndarray, invalid_actions: List[int]) -> int:
        # --- 表現ネットワークから初期状態を取得
        s0 = self.parameter.representation_network(state[np.newaxis, ...])
        s0_str = self.s0.ref()
        
        # --- シミュレーションしてpolicyを作成
        for _ in range(self.config.num_simulations):
            self._simulation(s0, s0_str, invalid_actions, is_afterstate=False)

        確率に比例したアクションを選択（コードは同じなので省略）
        
        return action

    # --- シミュレーション（1step,再帰,次の報酬を返す）
    def _simulation(self, state, state_str, invalid_actions, is_afterstate, depth: int = 0):
        if depth >= 99999:  # for safety
            return 0

        # stateとafterstateの場合で処理が異なる
        if not is_afterstate:
            # PVを予測
            self._init_state(state_str, self.config.action_num)
            self.parameter.prediction(state, state_str)

            # actionを選択
            puct_list = self._calc_puct(state_str, invalid_actions, depth == 0)
            action = random.choice(np.where(puct_list == np.max(puct_list))[0])

            # 次の状態を取得(after state)
            n_state = self.parameter.afterstate_dynamics_network(state, [action])
            reward = 0
            is_afterstate = True

        else:
            # QCを予測
            self._init_state(state_str, self.config.codebook_size)
            self.parameter.afterstate_prediction(state, state_str)

            # codeを選択
            c = self.parameter.C[state_str]
            action = np.argmax(c[0])  # outcomes

            # 次の状態と報酬を取得
            n_state, reward_category = self.parameter.dynamics_network(state, c)
            reward = float_category_decode(reward_category.numpy()[0], self.config.v_min)
            is_afterstate = False

        n_state_str = n_state.ref()
        enemy_turn = self.config.env_player_num > 1  # 2player以上は相手番と決め打ち

        if self.N[state_str][action] == 0:
            # leaf node ならロールアウト
            if is_afterstate:
                self.parameter.afterstate_prediction(n_state, n_state_str)
                n_reward = self.parameter.Q[n_state_str]
            else:
                self.parameter.prediction(n_state, n_state_str)
                n_reward = self.parameter.V[n_state_str]
        else:
            # 子ノードに降りる(展開)
            n_reward = self._simulation(n_state, n_state_str, [], is_afterstate, depth + 1)

        # 次が相手のターンなら、報酬は最小になってほしいので-をかける
        if enemy_turn:
            n_reward = -n_reward

        # 割引報酬
        reward = reward + self.config.discount * n_reward

        self.N[state_str][action] += 1
        self.W[state_str][action] += reward
        self.Q[state_str][action] = self.W[state_str][action] / self.N[state_str][action]

        self.parameter.q_min = min(self.parameter.q_min, self.Q[state_str][action])
        self.parameter.q_max = max(self.parameter.q_max, self.Q[state_str][action])

        return reward

    def _calc_puct(self, state_str, invalid_actions, is_root):

        # ディリクレノイズ
        if is_root:
            dir_alpha = self.config.root_dirichlet_alpha
            if self.config.root_dirichlet_adaptive:
                dir_alpha = 1.0 / np.sqrt(self.config.action_num - len(invalid_actions))
            noises = np.random.dirichlet([dir_alpha] * self.config.action_num)

        以降は同じ
        return scores
      

Trainer

6つのネットワークを同時に学習させます。
疑似コードにはないですが、VQ-VAEも混ぜて学習させています。

class Trainer(RLTrainer):
    def __init__(self, *args):
        super().__init__(*args)

        self.optimizer = keras.optimizers.Adam()
        # バッチ毎に出力
        self.cross_entropy_loss = keras.losses.CategoricalCrossentropy(axis=1, reduction=keras.losses.Reduction.NONE)
        self.train_count = 0

    def train(self):
        if self.remote_memory.length() < self.config.memory_warmup_size:
            return {}
        indices, batchs, weights = self.remote_memory.sample(self.train_count, self.config.batch_size)

        # (batch, dict, steps, val) -> (steps, batch, val)
        states_list = batchsよりデータ変換
        actions_list = batchsよりデータ変換
        policies_list = batchsよりデータ変換
        values_list = batchsよりデータ変換
        rewards_list = batchsよりデータ変換

        with tf.GradientTape() as tape:
            # --- 1st step
            hidden_states = self.parameter.representation_network(states_list[0])
            p_pred, v_pred = self.parameter.prediction_network(hidden_states)

            # loss
            policy_loss = self.cross_entropy_loss(policies_list[0], p_pred)
            v_loss = self.cross_entropy_loss(values_list[0], v_pred)
            reward_loss = tf.constant([0] * self.config.batch_size, dtype=tf.float32)
            chance_loss = tf.constant([0] * self.config.batch_size, dtype=tf.float32)
            q_loss = tf.constant([0] * self.config.batch_size, dtype=tf.float32)
            vae_loss = tf.constant([0] * self.config.batch_size, dtype=tf.float32)

            # --- unroll steps
            for t in range(self.config.unroll_steps):
                after_states = self.parameter.afterstate_dynamics_network(hidden_states, actions_list[t])
                chance_pred, q_pred = self.parameter.afterstate_prediction_network(after_states)
                chance_code, chance_vae_pred = self.parameter.vq_vae(states_list[t + 1])

                chance_loss += self.cross_entropy_loss(chance_code, chance_pred)
                q_loss += self.cross_entropy_loss(values_list[t], q_pred)
                vae_loss += tf.reduce_mean(tf.square(chance_code - chance_vae_pred), axis=1)  # MSE

                hidden_states, rewards_pred = self.parameter.dynamics_network(after_states, chance_code)
                p_pred, v_pred = self.parameter.prediction_network(hidden_states)

                policy_loss += self.cross_entropy_loss(policies_list[t + 1], p_pred)
                v_loss += self.cross_entropy_loss(values_list[t + 1], v_pred)
                reward_loss += self.cross_entropy_loss(rewards_list[t], rewards_pred)

            loss = v_loss + policy_loss + reward_loss + chance_loss + q_loss + self.config.commitment_cost * vae_loss
            loss = tf.reduce_mean(loss * weights)

            # 各ネットワークの正則化項を加える
            loss += tf.reduce_sum(self.parameter.representation_network.losses)
            loss += tf.reduce_sum(self.parameter.prediction_network.losses)
            loss += tf.reduce_sum(self.parameter.dynamics_network.losses)
            loss += tf.reduce_sum(self.parameter.afterstate_dynamics_network.losses)
            loss += tf.reduce_sum(self.parameter.afterstate_prediction_network.losses)
            loss += tf.reduce_sum(self.parameter.vq_vae.losses)

        priorities = v_loss.numpy()

        # lr
        lr = self.config.lr_init * self.config.lr_decay_rate ** (self.train_count / self.config.lr_decay_steps)
        self.optimizer.learning_rate = lr

        variables = [
            self.parameter.representation_network.trainable_variables,
            self.parameter.dynamics_network.trainable_variables,
            self.parameter.prediction_network.trainable_variables,
            self.parameter.afterstate_dynamics_network.trainable_variables,
            self.parameter.afterstate_prediction_network.trainable_variables,
            self.parameter.vq_vae.trainable_variables,
        ]
        grads = tape.gradient(loss, variables)
        for i in range(len(variables)):
            self.optimizer.apply_gradients(zip(grads[i], variables[i]))

        self.train_count += 1

        # memory update
        self.remote_memory.update(indices, batchs, priorities)

        # 学習したらキャッシュは削除
        self.parameter.reset_cache()
        return {}

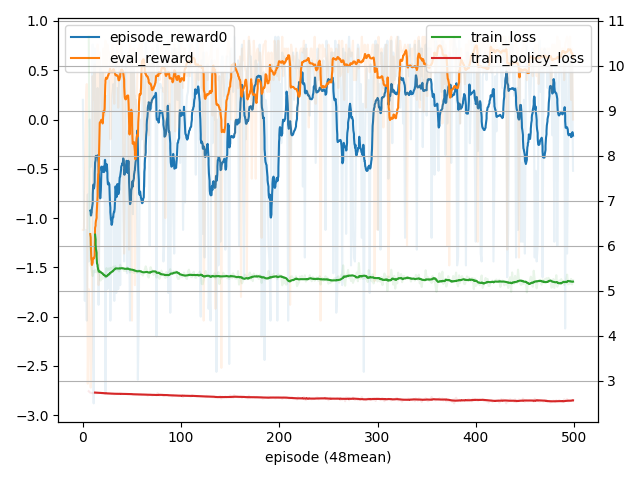
学習

ネットワークは増えましたがMuZeroからかなり学習しやすくなった印象を受けました。
本フレームワークで一番簡単なGridを学習させたコードを乗せておきます。
（Gridは移動確率が80％なので確率的な遷移をします。なのでMuZeroでは学習が難しい）

学習に使ったコードは github を参照してください。

詳細

mean 0.28000000715255735
### env: Grid, rl: StochasticMuZero, max episodes: 1, timeout:  -1.00s, max steps: -1, max train: -1
### 0, action 3, rewards [0.], next 0
env   None
work0 None
......
.   G.
. . X.
.P   .
......


V: -0.13093
 ←  :  20.0%       2(N)  -0.12651(Q),   0.69859(PUCT),   0.20266(P),  -0.14124(Q_pred),   3(code),  -0.04024(reward)
 ↓  :  20.0%       2(N)  -0.14420(Q),   0.78947(PUCT),   0.27717(P),  -0.16114(Q_pred),   3(code),  -0.03734(reward)
 →  :  20.0%       2(N)  -0.14180(Q),   0.69285(PUCT),   0.20312(P),  -0.14771(Q_pred),   3(code),  -0.03839(reward)
*↑  :  40.0%       4(N)  -0.07325(Q),   0.70428(PUCT),   0.31705(P),  -0.07971(Q_pred),   3(code),  -0.03292(reward)

### 1, action 3, rewards [-0.04], next 0
env   {}
work0 {}
......
.   G.
.P. X.
.    .
......


V: -0.00344
 ←  :  20.0%       2(N)  -0.05015(Q),   0.72786(PUCT),   0.20085(P),  -0.05568(Q_pred),   3(code),  -0.04535(reward)
 ↓  :  10.0%       1(N)  -0.10166(Q),   0.75672(PUCT),   0.15930(P),  -0.11296(Q_pred),   3(code),  -0.03797(reward)
 →  :  30.0%       3(N)  -0.00101(Q),   0.71764(PUCT),   0.23687(P),  -0.01539(Q_pred),   3(code),  -0.03856(reward)
*↑  :  40.0%       4(N)   0.07266(Q),   0.83272(PUCT),   0.40298(P),   0.07426(Q_pred),   3(code),  -0.03768(reward)

### 2, action 3, rewards [-0.04], next 0
env   {}
work0 {}
......
.P  G.
. . X.
.    .
......


V: 0.17289
 ←  :  10.0%       1(N)   0.03672(Q),   0.79151(PUCT),   0.14788(P),   0.04080(Q_pred),   3(code),  -0.04266(reward)
 ↓  :  10.0%       1(N)   0.00878(Q),   0.74439(PUCT),   0.12991(P),   0.00976(Q_pred),   3(code),  -0.03501(reward)
 →  :  40.0%       4(N)   0.28727(Q),   0.83873(PUCT),   0.29811(P),   0.31947(Q_pred),   3(code),  -0.03755(reward)
*↑  :  40.0%       4(N)   0.14442(Q),   0.87917(PUCT),   0.42410(P),   0.16938(Q_pred),   3(code),  -0.03691(reward)

### 3, action 2, rewards [-0.04], next 0
env   {}
work0 {}
......
.P  G.
. . X.
.    .
......


V: 0.17289
 ←  :  10.0%       1(N)   0.03672(Q),   0.79151(PUCT),   0.14788(P),   0.04080(Q_pred),   3(code),  -0.04266(reward)
 ↓  :  10.0%       1(N)   0.00878(Q),   0.74439(PUCT),   0.12991(P),   0.00976(Q_pred),   3(code),  -0.03501(reward)
*→  :  40.0%       4(N)   0.28727(Q),   0.83873(PUCT),   0.29811(P),   0.31947(Q_pred),   3(code),  -0.03755(reward)
 ↑  :  40.0%       4(N)   0.14442(Q),   0.87917(PUCT),   0.42410(P),   0.16938(Q_pred),   3(code),  -0.03691(reward)

### 4, action 2, rewards [-0.04], next 0
env   {}
work0 {}
......
. P G.
. . X.
.    .
......


V: 0.46758
 ←  :  10.0%       1(N)   0.10575(Q),   0.72235(PUCT),   0.09844(P),   0.11750(Q_pred),   3(code),  -0.04668(reward)
 ↓  :  10.0%       1(N)   0.24098(Q),   0.87459(PUCT),   0.14708(P),   0.26775(Q_pred),   3(code),  -0.03716(reward)
*→  :  60.0%       6(N)   0.51332(Q),   0.97630(PUCT),   0.49499(P),   0.56149(Q_pred),   3(code),  -0.03821(reward)
 ↑  :  20.0%       2(N)   0.32794(Q),   0.96188(PUCT),   0.25949(P),   0.34071(Q_pred),   3(code),  -0.04481(reward)

### 5, action 2, rewards [-0.04], next 0
env   {}
work0 {}
......
.  PG.
. . X.
.    .
......


V: 0.76773
 ←  :   0.0%       0(N)   0.00000(Q),   0.63178(PUCT),   0.03740(P),   0.22425(Q_pred),   3(code),  -0.07277(reward)
 ↓  :  10.0%       1(N)   0.20154(Q),   0.68202(PUCT),   0.05796(P),   0.22394(Q_pred),   3(code),   0.15755(reward)
*→  :  70.0%       7(N)   0.76054(Q),   1.14485(PUCT),   0.69939(P),   0.83461(Q_pred),   3(code),   0.76091(reward)
 ↑  :  20.0%       2(N)   0.61084(Q),   1.00764(PUCT),   0.20525(P),   0.68528(Q_pred),   3(code),   0.08008(reward)

### 6, action 2, rewards [1.], done(env), next 0
env   {}
work0 {}
......
.   P.
. . X.
.    .
......

Q_predとrewardがちゃんと学習できていますね。(rewardはもうちょっと学習できそうですが)

最後に

すごい力技に見えますけど、これで学習できちゃうのがすごいですね。