この記事は自作している強化学習フレームワーク SimpleDistributedRL の解説記事です。
はじめに
モンテカルロ木探索から AlphaZero の間には AlphaGo と AlphaGoZero があります。
しかしこの2つは囲碁に特化しているのでフレームワーク上の実装としては AlphaZero からにしたいと思います。
参考
・AlphaGoZero論文 Mastering the Game of Go without Human Knowledge
・AlphaZero論文 A general reinforcement learning algorithm that masters chess, shogi and Go through self-play
・AlphaZero論文(更新版) A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play | published in the journal Science (Open Access version)
・AlphaZero論文の日本語訳ブログ AlphaZeroの論文 | TadaoYamaokaの開発日記
・DeepMindのAlphaZeroの記事 AlphaZero: Shedding new light on chess, shogi, and Go | DeepMind
・AlphaZeroについてとても分かりやすいブログ スッキリわかるAlphaZero | どこから見てもメンダコ
・A Simple Alpha(Go) Zero Tutorial
AlphaZero
モンテカルロ木探索の問題点
モンテカルロ木探索では大きく2つの問題があります。
- UCT値を求めるにあたって、全アクションを最低1回実行する必要がある(囲碁の初手は361通り)
- ロールアウトの結果がランダムプレイに依存し精度が低い
これら問題を解決した手法がAlphaZeroとなります。
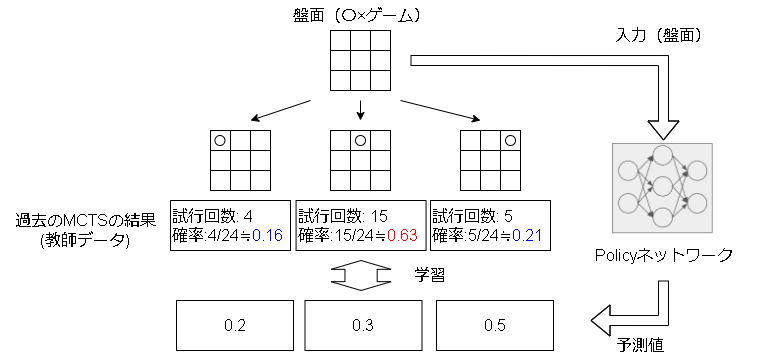
教師あり学習によるアクションの予測
前述の通り、UCT値によるアクションの選択は0回のアクションに対して評価できない問題がありました。
これを解決するために、過去のMCTSの結果を近似(再現)するニューラルネットワークを考えます。
過去のMCTSの結果を参考にする事で、未知の盤面でもある程度有効なアクションを推測する事が狙いです。
各アクションの確率 $\pi$ は試行回数を元に以下で計算されます。
$$
\pi(a|s) = \frac{N(s, a)^{\frac{1}{\tau}}}{ \sum_b N(s,b)^{\frac{1}{\tau}}}
$$
$N(s,a)$ がアクションの試行回数、$\tau$ は探索パラメータで最初の30手は $\tau=1$(回数に比例した確率選択)、それ以降は $\tau \rightarrow 0$(最大回数の選択と同じ)です。
これで有効そうなアクションを計算できるようになったのでUCTに組み込みます。(PUCT)
PUCT $U(s,a)$ は以下となります。
\begin{align}
U(s,a) = C(s)P(s,a) \frac{\sqrt{N(s)}}{1 + N(s,a)} \\
C(s) = \log{ \frac{1 + N(s) + C_{base}}{C_{base}} } + C_{init}
\end{align}
$P(s,a)$ がPolicyネットワークの予測値、$N(s,a)$ がアクションの試行回数、$N(s)$ が全アクションの試行回数です。
($C_{base}$と$C_{init}$はハイパーパラメータ)
以前は$C(s)$がハイパーパラメータ $c_{puct}$ でしたが変更があったようです。(AlphaZeroの論文 | TadaoYamaokaの開発日記より)
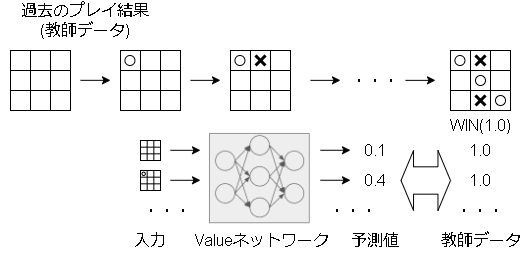
盤面の勝率の学習(ロールアウトの改善)
ロールアウトはランダムプレイ(モンテカルロ法)で勝率を出していましたが、ここもニューラルネットワークに置き換えて精度を上げる事を考えます。
ある盤面について、過去のプレイ結果を元に教師あり学習する事で、今の盤面の勝率を予測します。
ロールアウトの結果をValueネットワークの結果に置き換えることで、ランダムプレイが不要になり精度と探索時間が大きく向上しました。
(これによりモンテカルロ法の要素がなくなりましたねw)
またこれにより、MCTSでは子の展開はnシミュレーションに1回行っていたのをAlphaZeroでは子のノードを1シミュレーションに1回展開するように変更されています。
(正確にはAlphaGoZeroから変更)
(理由は多分探索にかかる時間が大幅に減ったからだと思われます)
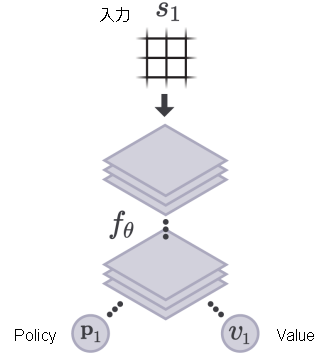
Policy-Valueネットワーク
上記2つのネットワークですが、実際には1つのニューラルネットワークで表現します。
これはマルチタスク学習といい、機械学習で割とある手法です。
タスク間で共通する特徴が学習でき、精度向上が見込めます。(マルチタスク学習とは | AI研)
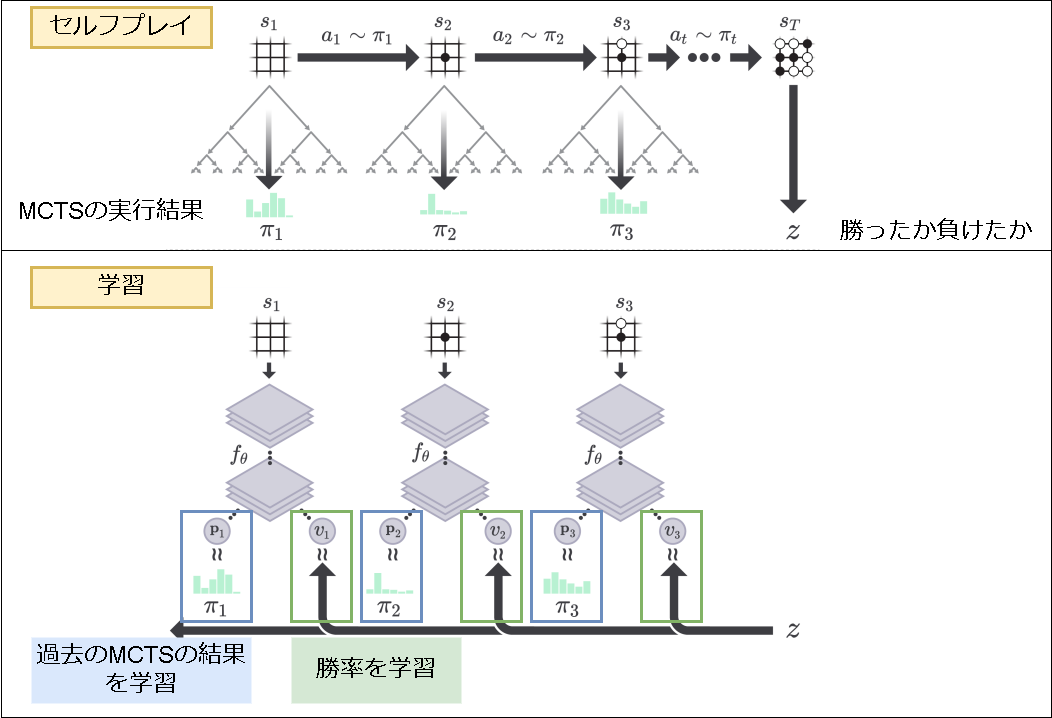
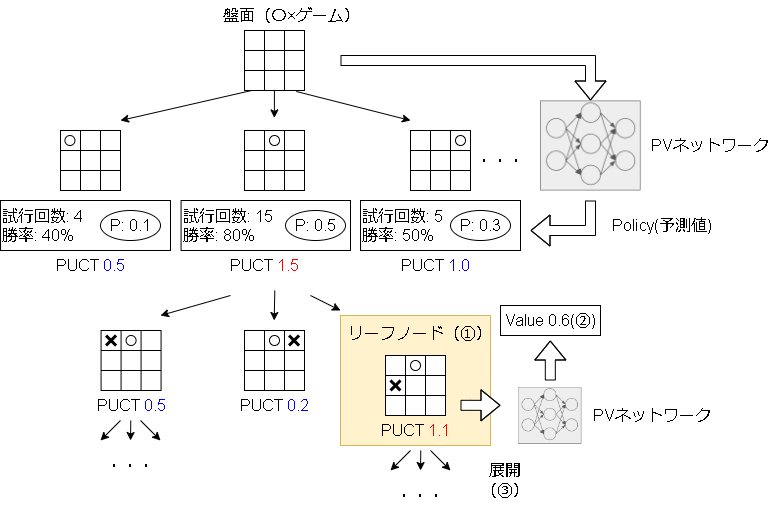
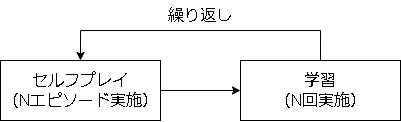
ここまでの内容をまとめると以下になります。
(論文の画像を元に追記)
図の上がセルフプレイによる経験の蓄積で、MCTSの実行結果(Policy)と勝率を保存します。
図の下が学習フェーズで、保存した経験を元に教師あり学習をします。
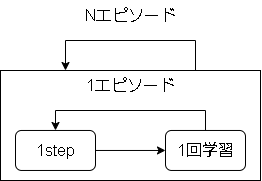
次にセルフプレイ時のアクションですが、アクションはシミュレーション時に選択された回数で決まります。
シミュレーション時のアクションの選択は以下です。
①PUCTに従いリーフノードまで降りる
②ロールアウトの代わりに予測したValue(勝率)を上に返す
③(次のために)子ノードを展開する
その他のテクニックや補足内容
アクションのディリクレノイズ
シミュレーション時のrootノードですが、アクションの選択にディリクレノイズ(dirichlet noise)を追加し、探索を促します。
具体的にはPolicyの予測値 $P(s,a)$ が以下になります。
$$
P(s,a) = (1 - \epsilon) p_a + \epsilon \eta_a
$$
$p_a$ が元の予測値、$\epsilon$ が反映率、$\eta_a$ がディリクレノイズ(alpha=0.03)です。
学習率
段階的に下げていきます。
最初は0.2に設定され、チェスと将棋では10万、30万、50万ステップ、囲碁では0、30万、50万ステップ後にそれぞれ0.02、0.002、0.0002に変えるそうです。
トレーニングに使う経験
過去50万回のセルフプレイした経験より、ランダムで取り出して4096のミニバッチを作成します。
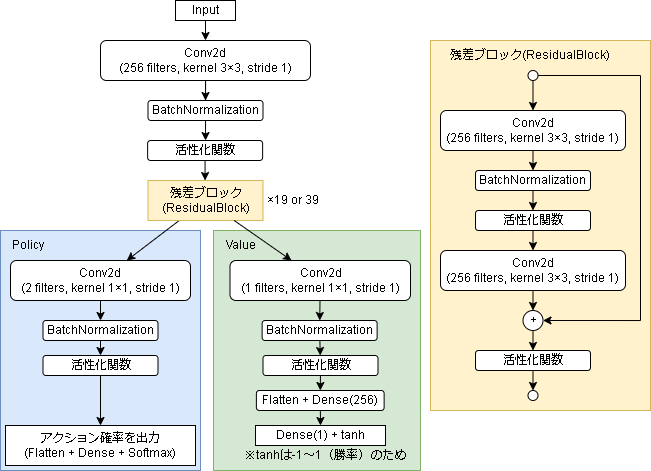
ネットワーク構造
入力層
ここは各ドメインに特化した内容になっています。
囲碁
入力は 19×19×17 の画像レイヤーで、19×19が盤面に相当します。
17層の内訳は以下です。
| 層数 | ||
|---|---|---|
| 黒石の位置×履歴(過去8手) | 1×8 | |
| 白石の位置×履歴(過去8手) | 1×8 | |
| 手番 | 1 | 黒ならすべて1、白ならすべて0 |
過去8手の履歴を保存しているのはループへの対応(多分禁じ手であるコウへの対応)、手番を保存しているのはコミ(先手有利なので囲碁にはハンデがつく)を学習させるためとの記載があります。
チェス
入力は 8×8×119 の画像レイヤーで、8×8が盤面に相当します。
119層の内訳は以下です。
| 層数 | 備考 | |
|---|---|---|
| 各自コマの位置×履歴(過去8手) | 6×8 | |
| 各相手コマの位置×履歴(過去8手) | 6×8 | |
| 過去同じ盤面が1回あったか×履歴(過去8手)① | 1×8 | すべて1or0 |
| 過去同じ盤面が2回あったか×履歴(過去8手)① | 1×8 | すべて1or0 |
| 手番 | 1 | 自ならすべて1、相手ならすべて0 |
| 総手数 | 1 | |
| 自側でキャスリングできるか | 2 | キング側とクイーン側でそれぞれ1層 |
| 相手側でキャスリングできるか | 2 | キング側とクイーン側でそれぞれ1層 |
| コマ交換がなく、ポーンが動いていない手数② | 1 |
①はチェスに3回同一場面が現れたら引き分けになるというルールに対応しています。
②は50手以上コマ交換がなく、ポーンが動いていないと引き分けにできるというルールに対応しています。
総手数などの実数値は多分実数値ですべて埋めた値だと思いますが論文の内容を読んだだけだとちょっと自信がありません。
将棋
入力は 9×9×362 の画像レイヤーで、9×9が盤面に相当します。
362層の内訳は以下です。
| 層数 | 備考 | |
|---|---|---|
| 各自コマの位置×履歴(過去8手) | (8+6)×8 | 8+6は駒+成駒 |
| 各相手コマの位置×履歴(過去8手) | (8+6)×8 | 8+6は駒+成駒 |
| 過去同じ盤面が1回あったか×履歴(過去8手)① | 1×8 | すべて1or0 |
| 過去同じ盤面が2回あったか×履歴(過去8手)① | 1×8 | すべて1or0 |
| 過去同じ盤面が3回あったか×履歴(過去8手)① | 1×8 | すべて1or0 |
| 各自持ち駒の数×履歴(過去8手) | 7×8 | |
| 各相手持ち駒の数×履歴(過去8手) | 7×8 | |
| 手番 | 1 | 自ならすべて1、相手ならすべて0 |
| 総手数 | 1 |
①はチェスと同様、千日手と呼ばれる4回同一場面が現れたら引き分けになるルールに対応しています。
出力層
出力層は各アクションの確率(と勝率)です。
囲碁・将棋・チェスにより異なり、またドメインに特化する内容なので本記事では省略します。
中間層
AlphaGoZeroとの違い
論文に載っていた違いになります。
- 碁は勝ち負けだけなので勝率を推定していましたが、将棋とチェスは引き分けもあるためそれも含めた結果を推定しています。
(「勝率+1,負け+0」 → 「勝率+1,引き分け+0,負け-1」 への変更かと思われます) - AlphaGoZeroでは碁の対称性を利用してデータを水増し(反転、回転)を実施、AlphaZeroは水増しなし
- AlphaGoZeroではベストプレイヤーを保持し、勝率55%を超えると現プレイヤーと交換。AlphaZeroは同じプレイヤー同士でひたすらプレイ。
- AlphaGoZeroはベイズ最適化によって検索のハイパーパラメータを調整。 AlphaZeroではゲーム固有の調整なしで、すべてのゲームに同じハイパーパラメータを利用。
ただし、探索ノイズ(ディリクレノイズ)と学習率のスケジューリングは例外。
実装
モンテカルロ木探索と同じで実装はマルコフ過程のモデルを想定します。
ただ状態は連続値を取ると数を数えれなくなるので実際に学習できるかは別の話になります。
フレームワーク上の実装はgithubを見てください。
(関係のある箇所のみを抜粋しています)
実装時の細かい話
結構細かいところで実装はどうするんだろ?と思うところがありました。
なので以下2つの実装コードを参考に見ています。
①スッキリわかるAlphaZero | どこから見てもメンダコ
②PythonとKerasを使ってAlphaZero AIを自作する | POSTD
MCTSのキャッシュ
MCTSで保存される各ノードの勝率 $W$ と試行回数 $N$ ですが、①②ともエピソードの最初でリセットされるようです。
MCTSの勝率の伝播
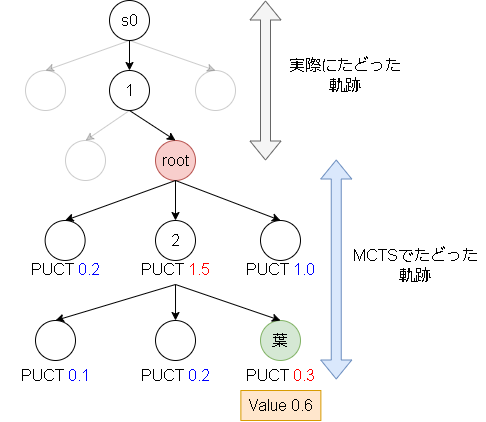
以下の図で説明します。
今rootの状態でMCTSをした場合、葉のノードで勝率0.6という結果を得ました。
この後の伝播方法が少し違いました。
①ではMCTSでたどった軌跡のみに伝播させています。(図で言うと[root,2,葉])
②はs0ノードまで伝播しています。([s0,1,root,2,葉])
1エピソード毎でキャッシュはクリアされるので、同じ状態に来ない前提なら①の実装で問題ない気がします。
なのでフレームワーク上は①の実装にしています。
アクションの正解データに関して
①では試行回数を元にした確率を正解データとしています。
②では最終的に選んだアクション(One-hotの形)を正解データにしていました。
フレームワーク上は①の実装にしています。
Config
ハイパーパラメータです。(碁の値)
@dataclass
class Config(DiscreteActionConfig):
simulation_times: int = 800 # 1stepで実行するシミュレーション回数
capacity: int = 500_000 # メモリ容量
gamma: float = 1.0 # 割引率
sampling_steps: int = 30 # 確率でアクションを選ぶ初手からのstep数
batch_size: int = 4096
warmup_size: int = 10000
# 学習率のスケジューリング
lr_schedule: List[dict] = [
{"train": 0, "lr": 0.02},
{"train": 300_000, "lr": 0.002},
{"train": 500_000, "lr": 0.0002},
]
# ディリクレノイズ
root_dirichlet_alpha: float = 0.3
root_exploration_fraction: float = 0.25
# PUCT
c_base: float = 19652
c_init: float = 1.25
Network
Tensorflowのカスタムモデルとして作成しています。
引数については②のコードを参考にしています。
まずは画像処理ブロック部分です。
残差ブロック(ResidualBlock)とfilter数は引数で変えることができます。
このモデルは画像形式(None,w,h,ch)を入力すると画像形式(None,w,h,filters)を返します。
import tensorflow.keras as keras
from tensorflow.keras import layers as kl
from tensorflow.keras import regularizers
class AlphaZeroImageBlock(keras.Model):
def __init__(
self,
n_blocks: int = 19,
filters: int = 256,
kernel_size=(3, 3),
l2: float = 0.0001,
):
super().__init__()
conv2d_params = dict(
filters=filters,
kernel_size=kernel_size,
padding="same",
use_bias=False,
activation="linear",
kernel_regularizer=regularizers.l2(l2),
)
self.conv1 = kl.Conv2D(**conv2d_params)
self.bn1 = kl.BatchNormalization()
self.act1 = kl.LeakyReLU()
self.resblocks = [_ResidualBlock(conv2d_params) for _ in range(n_blocks)]
def call(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.act1(x)
for resblock in self.resblocks:
x = resblock(x)
return x
class _ResidualBlock(keras.Model):
def __init__(self, conv2d_params):
super().__init__()
self.conv1 = kl.Conv2D(**conv2d_params)
self.bn1 = kl.BatchNormalization()
self.relu1 = kl.LeakyReLU()
self.conv2 = kl.Conv2D(**conv2d_params)
self.bn2 = kl.BatchNormalization()
self.relu2 = kl.LeakyReLU()
def call(self, x):
x1 = self.conv1(x)
x1 = self.bn1(x1)
x1 = self.relu1(x1)
x1 = self.conv2(x1)
x1 = self.bn2(x1)
x = x + x1
x = self.relu2(x)
return x
次にネットワーク全体です。
入力が(layers,w,h)の場合を想定した場合を書いています。
from tensorflow.keras import layers as kl
class _Network(keras.Model):
def __init__(self, config: Config):
super().__init__()
# 入力は (layers, width, height) の形
input_shape = (17, 19, 19) # 碁
in_layer = c = kl.Input(shape=input_shape)
# (n, width, height) -> (width, height, n)
c = kl.Permute((2, 3, 1))(c)
# ResNet
c = AlphaZeroImageBlock(n_blocks=19, filters=256)(c)
# Conv2D層の引数
_conv2d_params = dict(
padding="same",
use_bias=False,
activation="linear",
kernel_regularizer=regularizers.l2(0.0001),
)
# --- policy
c1 = kl.Conv2D(2, kernel_size=(1, 1), **_conv2d_params)(c)
c1 = kl.BatchNormalization()(c1)
c1 = kl.LeakyReLU()(c1)
c1 = kl.Flatten()(c1)
policy = kl.Dense(config.action_num, activation="softmax")(c1)
# --- value
c2 = kl.Conv2D(1, kernel_size=(1, 1), **_conv2d_params)(c)
c2 = kl.BatchNormalization()(c2)
c2 = kl.LeakyReLU()(c2)
c2 = kl.Flatten()(c2)
c2 = kl.Dense(256, activation="relu")(c2)
value = kl.Dense(
1,
# activation="tanh", # 論文上はtanh(-1~1)です
)(c2)
self.model = keras.Model(in_state, [policy, value])
def call(self, state):
return self.model(state)
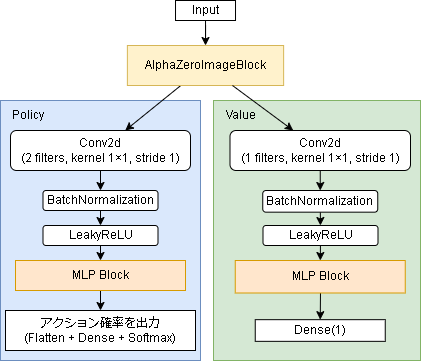
Valueの出力ですが、勝率を表すので論文ではtanhを採用していますが、フレームワーク上は範囲を限定したくないのでそのまま線形出力にしています。
また、フレームワーク上では上のコードとは少し異なり以下のようになっています。
PolicyとValueにMLP Blockを追加し、ここを引数で変えられるようにしています。(無くすことも可能)
Parameter
PVNetworkとその結果をキャッシュする仕組みを作ります。
キャッシュする理由は、シミュレーション中はPVの結果が変わらない(学習しない)ので何回も同じ状態を訪れるからです。
class Parameter(RLParameter):
def __init__(self, *args):
super().__init__(*args)
# PVネットワーク
self.network = _Network(self.config)
# cache用 (simulationで何回も使うので)
self.P = {}
self.V = {}
# 状態での方策と勝率を予測しキャッシュする
def pred_PV(self, state, state_str):
if state_str not in self.P:
p, v = self.network(np.asarray([state]))
self.P[state_str] = p[0].numpy()
self.V[state_str] = v[0][0].numpy()
# キャッシュクリア
def reset_cache(self):
self.P = {}
self.V = {}
remote_memory
セルフプレイの結果を保存し、学習時にはランダムに取り出します。
DQNのExperienceReplayBufferと同じです。(コードは省略)
Worker
まずは全体です。
シミュレーション部分は後述します。
class Worker(ModelBaseWorker):
# --- エピソードの最初に実行 ---
def call_on_reset(self, state: np.ndarray, env: EnvRun, worker: WorkerRun) -> None:
self.step = 0
self.history = []
self.N = {} # 訪問回数(s,a)
self.W = {} # 累計報酬(s,a)
def _init_state(self, state_str):
if state_str not in self.N:
self.N[state_str] = [0 for _ in range(self.config.action_num)]
self.W[state_str] = [0 for _ in range(self.config.action_num)]
# --- stepのアクションを返す ---
def call_policy(self, state: np.ndarray, env: EnvRun, worker: WorkerRun) -> int:
self.state = state
self.state_str = str(state.tolist())
self.invalid_actions = env.get_invalid_actions(self.player_index)
self._init_state(self.state_str)
# --- シミュレーションしてpolicyを作成
# 環境は変えないようにバックアップ・リストアする
dat = env.backup()
for _ in range(self.config.simulation_times):
self._simulation(env, state, self.state_str, self.invalid_actions)
env.restore(dat)
# --- (教師データ) 試行回数を元に確率を計算
N = np.sum(self.N[self.state_str])
self.step_policy = [self.N[self.state_str][a] / N for a in range(self.config.action_num)]
# --- episodeの序盤は試行回数に比例した確率でアクションを選択、それ以外は最大試行回数
if self.step < self.config.sampling_steps:
action = random_choice_by_probs(self.N[self.state_str])
else:
counts = np.asarray(self.N[self.state_str])
action = random.choice(np.where(counts == counts.max())[0])
return int(action)
def call_on_step(
self,
next_state: np.ndarray,
reward: float,
done: bool,
env: EnvRun,
worker: WorkerRun,
):
self.step += 1
if not self.training:
return {}
self.history.append([self.state, self.step_policy, reward])
# 経験はエピソード終了時に報酬を逆伝播させて送る
if done:
reward = 0
for state, step_policy, step_reward in reversed(self.history):
reward = step_reward + self.config.gamma * reward
self.remote_memory.add(
{
"state": state,
"policy": step_policy,
"reward": reward,
}
)
return {}
simulation
シミュレーション部分です。
基本はMCTSと同じです。
class Worker(ModelBaseWorker):
# 1stepシミュレーションする(再帰)
# envのplayer手番の報酬を返す
def _simulation(
self,
env: EnvRun,
state: np.ndarray,
state_str: str,
invalid_actions,
depth: int = 0,
):
if depth >= env.max_episode_steps: # for safety
return 0
# 今のプレイヤーを保存
player_index = env.next_player_index
# PVを予測(actionでPを使用)
self._init_state(state_str)
self.parameter.pred_PV(state, state_str)
# actionを選択
puct_list = self._calc_puct(state_str, invalid_actions, depth == 0)
action = random.choice(np.where(puct_list == np.max(puct_list))[0])
# 1step進める
n_state, rewards, done = self.env_step(env, action)
reward = rewards[player_index]
n_state_str = to_str_observation(n_state)
enemy_turn = player_index != env.next_player_index
if done:
n_reward = 0
elif self.N[state_str][action] == 0:
# leaf node ならロールアウト
self.parameter.pred_PV(n_state, n_state_str) # Vを使用
n_reward = self.parameter.V[n_state_str]
else:
n_invalid_actions = self.get_invalid_actions(env)
# 子ノードに降りる(展開)
n_reward = self._simulation(env, n_state, n_state_str, n_invalid_actions, depth + 1)
# 前のプレイヤーの番と次のプレイヤーの番が違う場合、
# 相手側の報酬は最小になってほしいので-をかける
if enemy_turn:
n_reward = -n_reward
# 割引報酬
reward = reward + self.config.gamma * n_reward
# 結果を記録
self.N[state_str][action] += 1
self.W[state_str][action] += reward
return reward
def _calc_puct(self, state_str, invalid_actions, is_root):
# ディリクレノイズ
if is_root:
noises = np.random.dirichlet([self.config.root_dirichlet_alpha] * self.config.action_num)
# 各アクションのPUCT値を計算
N = np.sum(self.N[state_str])
scores = np.zeros(self.config.action_num)
for a in range(self.config.action_num):
if a in invalid_actions:
score = -np.inf
else:
# P(s,a): 過去のMCTSの結果を教師あり学習した結果
# U(s,a) = C(s) * P(s,a) * sqrt(N(s)) / (1+N(s,a))
# C(s) = log((1+N(s)+base)/base) + c_init
# score = Q(s,a) + U(s,a)
P = self.parameter.P[state_str][a]
# rootはディリクレノイズを追加
if is_root:
e = self.config.root_exploration_fraction
P = (1 - e) * P + e * noises[a]
n = self.N[state_str][a]
c = np.log((1 + N + self.config.c_base) / self.config.c_base) + self.config.c_init
u = c * P * (np.sqrt(N) / (1 + n))
q = 0 if n == 0 else self.W[state_str][a] / n
score = q + u
scores[a] = score
return scores
Trainer
学習部分です。
class Trainer(RLTrainer):
def __init__(self, *args):
super().__init__(*args)
# 学習率を扱いやすい形式に変換
self.lr_schedule = {}
for lr_list in self.config.lr_schedule:
self.lr_schedule[lr_list["train"]] = lr_list["lr"]
self.optimizer = keras.optimizers.Adam(learning_rate=self.lr_schedule[0])
self.train_count = 0
def train(self) -> dict:
# ある程度メモリにたまるまで学習しない
if self.remote_memory.length() < self.config.warmup_size:
return {}
# batch_size分ランダムに取り出す
batchs = self.remote_memory.sample(self.config.batch_size)
states = []
policies = []
rewards = []
for b in batchs:
states.append(b["state"])
policies.append(b["policy"])
rewards.append(b["reward"])
states = np.asarray(states)
policies = np.asarray(policies)
rewards = np.asarray(rewards).reshape((-1, 1))
with tf.GradientTape() as tape:
p_pred, v_pred = self.parameter.network(states)
# value: 状態に対する勝率(reward)を教師に学習(MSE)
value_loss = tf.square(rewards - v_pred)
# policy: 選んだアクション(MCTSの結果)を教師に学習(categorical cross entropy)
p_pred = tf.clip_by_value(p_pred, 1e-6, p_pred) # log(0)回避用
policy_loss = -tf.reduce_sum(policies * tf.math.log(p_pred), axis=1, keepdims=True)
loss = tf.reduce_mean(value_loss + policy_loss)
grads = tape.gradient(loss, self.parameter.network.trainable_variables)
self.optimizer.apply_gradients(zip(grads, self.parameter.network.trainable_variables))
self.train_count += 1
# lr_schedule
if self.train_count in self.lr_schedule:
self.optimizer.learning_rate = self.lr_schedule[self.train_count]
# 学習したらキャッシュは削除
self.parameter.reset_cache()
return {}
学習サイクルの違い(同期)
学習サイクルですが基本は非同期を前提にしています。
しかし、やはりいきなり非同期は難易度が高いので同期的な実装について見てみます。
①と②の実装が同期的に動く場合は以下のようになります。
本フレームワークを同期的に使うと以下になります。
大きな影響は、1エピソード中に方策が変わるというものですが、分散学習でも起こる現象なので結果に大きな影響はないと思います。
本フレームワークでも一応上の図のサイクルのように学習させることも可能です。
コード例は以下です。
import srl
from srl import runner
# --- env & algorithm load
from srl.envs import othello # isort: skip # noqa F401
from srl.algorithms import alphazero # isort: skip
def main():
# config
env_config = srl.EnvConfig("Othello")
rl_config = alphazero.Config(num_simulations=10, memory_warmup_size=100, batch_size=32)
rl_config.processors = [othello.LayerProcessor()]
config = runner.Config(env_config, rl_config)
config.model_summary()
# 学習ループ用
parameter = None
remote_memory = None
# --- 学習ループ
for _ in range(3):
# セルフプレイ(disable_trainer=Trueにすると経験取得のみになります)
# remote_memory に経験が入ります
config.players = [None, None]
parameter, remote_memory, history = runner.train(
config,
parameter=parameter,
remote_memory=remote_memory,
max_episodes=5,
disable_trainer=True,
)
# 学習のみ実施
parameter, remote_memory, history = runner.train_only(
config,
parameter=parameter,
remote_memory=remote_memory,
max_train_count=100,
)
# --- 学習結果
config.players = [None, "human"]
runner.render(config, parameter)
if __name__ == "__main__":
main()
学習サイクルの違い(AlphaGoZero)
AlphaGoZeroはベストプレイヤーを保持し続け、学習したプレイヤーと戦わせて55%の勝率を超えたら置き換えるというサイクルを回しています。
これを本フレームワークで実装すると以下になります。
import numpy as np
import srl
from srl import runner
# --- env & algorithm load
from srl.envs import othello # isort: skip # noqa F401
from srl.algorithms import alphazero # isort: skip
def main():
# config
env_config = srl.EnvConfig("Othello")
rl_config = alphazero.Config(num_simulations=10, memory_warmup_size=100, batch_size=64)
rl_config.processors = [othello.LayerProcessor()]
config = runner.Config(env_config, rl_config)
# --- ベストプレイヤーを保存するファイル
best_parameter_path = "_qiita_Othello_best.dat"
rl_config.parameter_path = best_parameter_path # ベストプレイヤーから毎回始める
best_rl_config = rl_config.copy() # ベストプレイヤー用の設定
remote_memory = None # 学習を通して経験を保存
# --- 学習ループ
for i in range(3):
# 学習用プレイヤー(None)とベストプレイヤー(best_rl_config)で対戦し学習
config.players = [None, best_rl_config]
parameter, remote_memory, history = runner.train(
config,
max_episodes=5,
remote_memory=remote_memory,
enable_evaluation=False,
)
# 学習後のプレイヤーを評価する(ベストプレイヤーと対戦)
config.players = [None, best_rl_config]
rewards = runner.evaluate(
config,
parameter,
max_episodes=5,
shuffle_player=True,
)
rewards = np.mean(rewards, axis=0)
print(f"------------ {i} evaluate: {rewards}")
# 学習用プレイヤー(None)の勝率が55%以上なら置きかえる
# 閾値は、勝ち:1、負け-1なので0.05
if rewards[0] > 0.05:
print("UPDATE!")
parameter.save(best_parameter_path)
# --- 学習結果
config.players = [None, "human"]
runner.render(config, parameter)
if __name__ == "__main__":
main()
学習結果
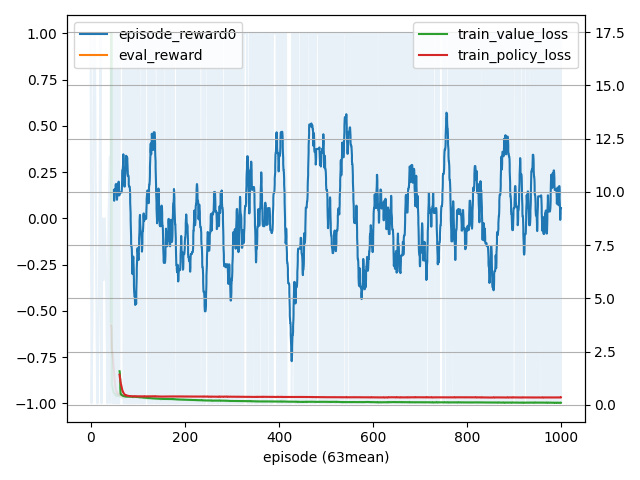
4×4マスのオセロを学習させてみました。(8×8は試行錯誤するには学習時間がかかりすぎました…)
コードは github
を参照してください。
- 学習経過
- 対戦結果
Average reward for 100 episodes: [ 0.38 -0.38], [None, 'random']
Average reward for 100 episodes: [-0.32 0.32], ['random', None]
Average reward for 100 episodes: [ 0.17 -0.17], [None, 'cpu']
Average reward for 100 episodes: [ 0.03 -0.04], ['cpu', None]
cpuは6手先を読んで最適解を打つプレイヤーです。
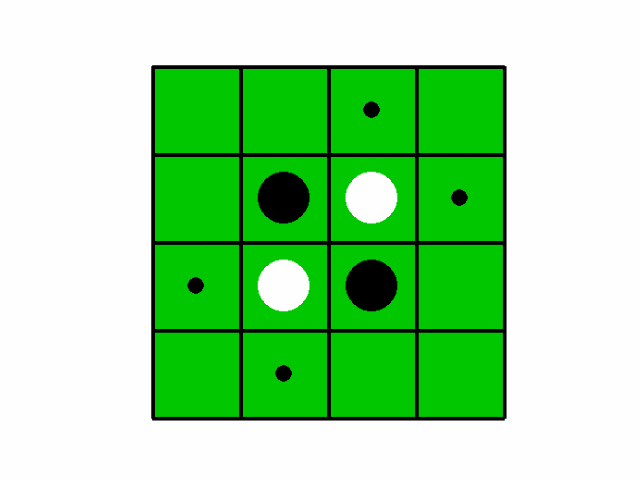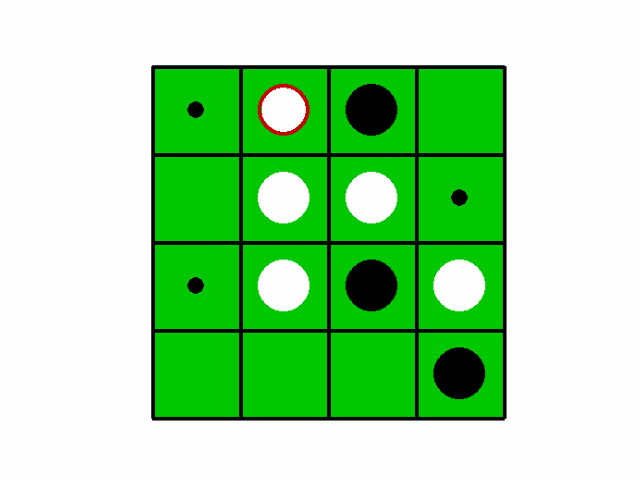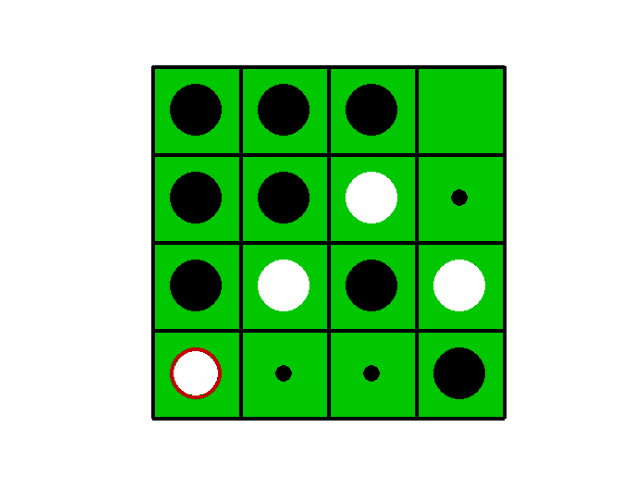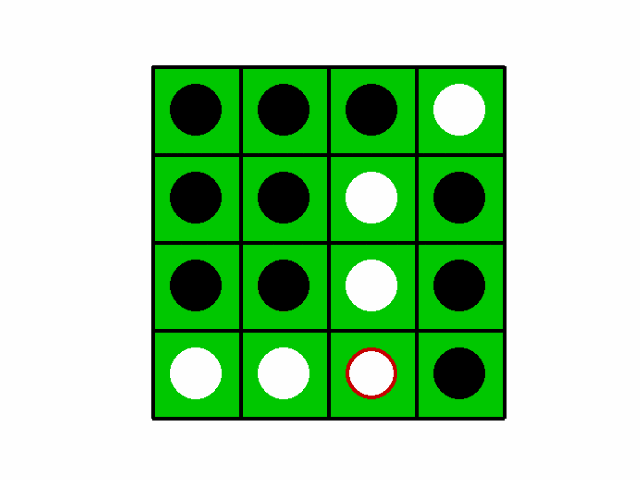
- 1プレイ例
先行が学習後のAIで後攻がcpuです。
詳細
### 0
-------------
| | | 2| |
| | o| x| 7|
| 8| x| o| |
| |13| | |
-------------
O: 2, X: 2
next player: O
V_net: -0.62205
2 : 1.0% ( 1)(N), -0.66838(Q), 0.06611(P_net), -0.25347(PUCT)
7 : 1.0% ( 1)(N), -0.59643(Q), 0.04851(P_net), -0.29199(PUCT)
*8 : 97.0% ( 97)(N), 0.98385(Q), 0.85238(P_net), 1.09302(PUCT)
13 : 1.0% ( 1)(N), -0.49064(Q), 0.03278(P_net), -0.28493(PUCT)
x0 : 0.0% ( 0)(N), 0.00000(Q), 0.00004(P_net), -inf(PUCT)
x1 : 0.0% ( 0)(N), 0.00000(Q), 0.00002(P_net), -inf(PUCT)
x3 : 0.0% ( 0)(N), 0.00000(Q), 0.00003(P_net), -inf(PUCT)
... Some invalid actions have been omitted. (invalid actions num: 12)
### 1, action 2, rewards [0 0], done False(), next 1
-------------
| | 1|*o| 3|
| | o| o| |
| | x| o|11|
| | | | |
-------------
O: 4, X: 1
next player: X
env_info : {}
work_info 0: None
train_info: None
- MinMax count: 0, 0.000s -
| |-500.0| | -0.0|
| | | | |
| | | | -0.0|
| | | | |
### 2, action 11, rewards [0 0], done False(), next 0
-------------
| | | o| |
| | o| o| |
| | x| x|*x|
|12|13|14|15|
-------------
O: 3, X: 3
next player: O
env_info : {}
work_info 1: None
train_info: None
V_net: -0.41406
12 : 1.0% ( 1)(N), -0.26903(Q), 0.02309(P_net), -0.12410(PUCT)
13 : 1.0% ( 1)(N), -0.79396(Q), 0.00864(P_net), -0.73977(PUCT)
14 : 1.0% ( 1)(N), -0.95312(Q), 0.20258(P_net), 0.31817(PUCT)
*15 : 97.0% ( 97)(N), 0.98610(Q), 0.76307(P_net), 1.08383(PUCT)
x0 : 0.0% ( 0)(N), 0.00000(Q), 0.00054(P_net), -inf(PUCT)
x1 : 0.0% ( 0)(N), 0.00000(Q), 0.00000(P_net), -inf(PUCT)
x2 : 0.0% ( 0)(N), 0.00000(Q), 0.00001(P_net), -inf(PUCT)
... Some invalid actions have been omitted. (invalid actions num: 12)
### 3, action 15, rewards [0 0], done False(), next 1
-------------
| | 1| o| 3|
| | o| o| |
| | x| o| x|
| | | |*o|
-------------
O: 5, X: 2
next player: X
env_info : {}
work_info 0: {}
train_info: None
- MinMax count: 0, 0.000s -
| | -0.0| | -0.0|
| | | | |
| | | | |
| | | | |
### 4, action 1, rewards [0 0], done False(), next 0
-------------
| 0|*x| o| |
| | x| x| 7|
| 8| x| o| x|
| | | | o|
-------------
O: 3, X: 5
next player: O
env_info : {}
work_info 1: {}
train_info: None
V_net: 0.03198
*0 : 84.0% ( 84)(N), 0.99867(Q), 0.69913(P_net), 1.10191(PUCT)
7 : 1.0% ( 1)(N), -0.09671(Q), 0.00036(P_net), -0.09442(PUCT)
8 : 15.0% ( 15)(N), 0.96349(Q), 0.13612(P_net), 1.07027(PUCT)
x1 : 0.0% ( 0)(N), 0.00000(Q), 0.00002(P_net), -inf(PUCT)
x2 : 0.0% ( 0)(N), 0.00000(Q), 0.00046(P_net), -inf(PUCT)
x3 : 0.0% ( 0)(N), 0.00000(Q), 0.00001(P_net), -inf(PUCT)
... Some invalid actions have been omitted. (invalid actions num: 13)
### 5, action 0, rewards [0 0], done False(), next 1
-------------
|*o| o| o| |
| 4| o| x| |
| | x| o| x|
| | |14| o|
-------------
O: 6, X: 3
next player: X
env_info : {}
work_info 0: {}
train_info: None
- MinMax count: 0, 0.001s -
| | | | |
| -0.0| | | |
| | | | |
| | | -0.0| |
### 6, action 4, rewards [0 0], done False(), next 0
-------------
| o| o| o| |
|*x| x| x| 7|
| 8| x| o| x|
| |13| | o|
-------------
O: 5, X: 5
next player: O
env_info : {}
work_info 1: {}
train_info: None
V_net: 0.93056
7 : 11.0% ( 11)(N), 0.98833(Q), 0.07759(P_net), 1.06949(PUCT)
*8 : 80.0% ( 80)(N), 0.99685(Q), 0.91726(P_net), 1.13898(PUCT)
13 : 9.0% ( 9)(N), 1.00781(Q), 0.00302(P_net), 1.01160(PUCT)
x0 : 0.0% ( 0)(N), 0.00000(Q), 0.00000(P_net), -inf(PUCT)
x1 : 0.0% ( 0)(N), 0.00000(Q), 0.00001(P_net), -inf(PUCT)
x2 : 0.0% ( 0)(N), 0.00000(Q), 0.00015(P_net), -inf(PUCT)
... Some invalid actions have been omitted. (invalid actions num: 13)
### 7, action 8, rewards [0 0], done False(), next 1
-------------
| o| o| o| |
| o| o| x| |
|*o| o| o| x|
|12| |14| o|
-------------
O: 9, X: 2
next player: X
env_info : {}
work_info 0: {}
train_info: None
- MinMax count: 0, 0.000s -
| | | | |
| | | | |
| | | | |
| -0.0| | -0.0| |
### 8, action 12, rewards [0 0], done False(), next 0
-------------
| o| o| o| |
| o| o| x| 7|
| o| x| o| x|
|*x|13|14| o|
-------------
O: 8, X: 4
next player: O
env_info : {}
work_info 1: {}
train_info: None
V_net: 0.90549
*7 : 97.0% ( 97)(N), 1.00022(Q), 0.99681(P_net), 1.12789(PUCT)
13 : 3.0% ( 3)(N), 0.43096(Q), 0.00297(P_net), 0.44028(PUCT)
14 : 0.0% ( 0)(N), 0.00000(Q), 0.00001(P_net), 0.00012(PUCT)
x0 : 0.0% ( 0)(N), 0.00000(Q), 0.00001(P_net), -inf(PUCT)
x1 : 0.0% ( 0)(N), 0.00000(Q), 0.00000(P_net), -inf(PUCT)
x2 : 0.0% ( 0)(N), 0.00000(Q), 0.00010(P_net), -inf(PUCT)
... Some invalid actions have been omitted. (invalid actions num: 13)
### 9, action 7, rewards [0 0], done False(), next 1
-------------
| o| o| o| 3|
| o| o| o|*o|
| o| x| o| o|
| x| | | o|
-------------
O: 11, X: 2
next player: X
env_info : {}
work_info 0: {}
train_info: None
- MinMax count: 3, 0.000s -
| | | |-500.0|
| | | | |
| | | | |
| | | | |
### 10, action 3, rewards [0 0], done False(), next 0
-------------
| o| o| o|*x|
| o| o| x| o|
| o| x| o| o|
| x|13|14| o|
-------------
O: 10, X: 4
next player: O
env_info : {}
work_info 1: {}
train_info: None
V_net: 1.05072
*13 : 91.0% ( 91)(N), 1.00033(Q), 0.98354(P_net), 1.13451(PUCT)
14 : 9.0% ( 9)(N), 1.00000(Q), 0.01186(P_net), 1.01489(PUCT)
x0 : 0.0% ( 0)(N), 0.00000(Q), 0.00000(P_net), -inf(PUCT)
x1 : 0.0% ( 0)(N), 0.00000(Q), 0.00001(P_net), -inf(PUCT)
x2 : 0.0% ( 0)(N), 0.00000(Q), 0.00005(P_net), -inf(PUCT)
... Some invalid actions have been omitted. (invalid actions num: 14)
### 11, action 13, rewards [0 0], done False(), next 1
-------------
| o| o| o| x|
| o| o| x| o|
| o| o| o| o|
| x|*o|14| o|
-------------
O: 12, X: 3
next player: X
env_info : {}
work_info 0: {}
train_info: None
- MinMax count: 0, 0.000s -
| | | | |
| | | | |
| | | | |
| | |-500.0| |
### 12, action 14, rewards [ 1 -1], done True(env), next 1
-------------
| o| o| o| x|
| o| o| x| o|
| o| o| x| o|
| x| x|*x| o|
-------------
O: 10, X: 6
next player: X
env_info : {'P1': 10, 'P2': 6}
work_info 1: {}
train_info: None
所感
仕組みは単純なのですが、実装時に困った所が多い印象でした。
また、学習環境が大規模スペックを想定しているので貧弱PCだと合ってるかどうかが分かりづらかったですね…。
論文の環境は、囲碁・チェス・将棋で、セルフプレイに第1世代のTPUを5000個、学習に第2世代のTPUを16個使用して 700,000 steps 学習させているらしいです。(チェスで9時間、将棋で12時間、囲碁で13日間かかったとのこと)
その他気になったことは以下です。(私の勝手な考えですので正確ではない点は注意してください)
-
Valueの教師あり学習
教師あり学習といいつつ同じ盤面で違う教師データになる場合があります。
例えばOXゲームの初期状態は0(引き分け)ですが、勝てば1、負ければ-1の教師データが混在します。
ということはValueによる学習は直感的には勝率の学習というより、勝率の平均値(期待値)を学習するというほうが正しいかもしれません。
またこの性質か分かりませんが、学習するにはバッチサイズがある程度大きい必要があるように感じます。
(これが関係あるかは不明ですが、論文のミニバッチは4096とかなり大きな数です) -
(モンテカルロ)木探索の役割
Value(盤面の評価値)が完璧の場合、木探索は不要です。
実際にOXゲームで木探索をせず完璧な評価値を返す実装をしてみましたが、理論値通りに動きました。
ただ、Valueはあくまで予測値なので、実際にN手先を見て値が正確かを確かめる意味合いで木探索があるかなと思いました。 -
勝率(value)は教師あり学習で学習できるのか?
教師として使う勝率ですが、対戦相手によって変動するような…?
セルフプレイなので最終的には強い相手に特化した勝率に収束すると思います。
強化学習的に見るとoff-policyな学習に見え、そこら辺の調整もしていないのに学習できるのが少し不思議な感じでした。