この記事は自作している強化学習フレームワーク SimpleDistributedRL の解説記事です。
はじめに
モンテカルロ木探索は強化学習のアルゴリズムというより木探索アルゴリズムの一種という位置付けです。
ただこれの発展系として、AlphaGo,AlphaZero,MuZeroといった有名なアルゴリズムがあるのでまずは説明していきたいと思います。
また以前に記事(第11回 今更だけど基礎から強化学習を勉強する モンテカルロ木探索編)を書いていますが、フレームワークに沿った内容として改めて書いています。
モンテカルロ法(Monte Carlo method; MC)
モンテカルロ法をざっくり言うと、適当な回数ランダムに実行してみてその結果から結論を導くアルゴリズムです。
主に確率または期待値の近似値を求める手法として使われます。
(強化学習では予測値を求める手法としてモンテカルロ法がありますがそれとは別ものです)
円周率を求める事例が多いですが、カードの例でやり方を見てみます。
問題 :デッキが30枚、初手に5枚ドローするカードゲームがあります。あるキーカードが初手に欲しいです。キーカードを何枚入れれば初手にキーカードが来るでしょうか。ただし、1回マリガン(手札を入れ替える)出来るとします。
キーカードが1枚入ってる場合の確率、2枚の確率…とそれぞれの確率を比較して枚数を決めたいところです。
ここで統計学として厳密に確率を求めようとする場合、かなり難しいと思います。
しかし、こういう近似値で十分な確率を求めたい場合はモンテカルロ法を使うと簡単に出せます。
import random
# キーカードの枚数
for key_num in range(1, 20):
# モンテカルロ法: 適当にシミュレーションしてみる
simulation_num = 100000
included_key_num = 0
for i in range(simulation_num):
# 指定枚数入ったデッキを作成(1がキーカード)
deck = [0] * 30
for i in range(key_num):
deck[i] = 1
# ランダムに5枚引く
hands = random.sample(deck, 5)
# キーカードが入っていない場合は引き直し(マリガン)
if sum(hands) == 0:
hands = random.sample(deck, 5)
# キーカードが入っていればカウントを増やす
if sum(hands) > 0:
included_key_num += 1
# モンテカルロ法: シミュレーションの結果から確率の近似値を出す
prob = included_key_num / simulation_num
print(f"キーカード数: {key_num}, 確率 {prob*100:.2f}%")
実行結果は以下です。
キーカード数: 1, 確率 30.56%
キーカード数: 2, 確率 52.76%
キーカード数: 3, 確率 67.97%
キーカード数: 4, 確率 78.70%
キーカード数: 5, 確率 86.19%
キーカード数: 6, 確率 91.09%
キーカード数: 7, 確率 94.43%
キーカード数: 8, 確率 96.53%
キーカード数: 9, 確率 97.96%
キーカード数: 10, 確率 98.84%
キーカード数: 11, 確率 99.32%
キーカード数: 12, 確率 99.64%
キーカード数: 13, 確率 99.83%
キーカード数: 14, 確率 99.90%
キーカード数: 15, 確率 99.95%
キーカード数: 16, 確率 99.98%
キーカード数: 17, 確率 99.99%
キーカード数: 18, 確率 100.00%
キーカード数: 19, 確率 100.00%
実際に試行して確率を出す手法がモンテカルロ法です。
もちろんこれは近似値なので正確な値ではありませんが、目安としては十分かと思われます。
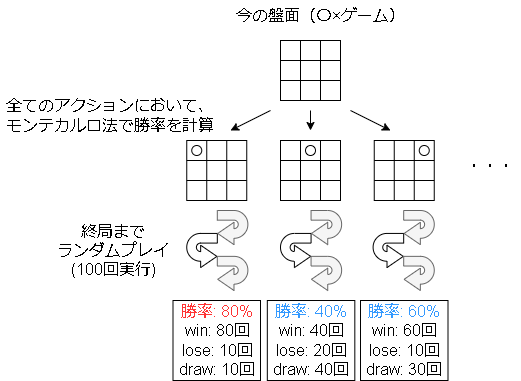
モンテカルロ探索(Monte Carlo Search; MCS)
まずは木を使わない場合の探索です。
アルゴリズムとしては各アクションに対してモンテカルロ法で勝率1を計算し、一番勝率が高いアクションを実行します。
モンテカルロ探索+UCT
モンテカルロ探索で問題となるのは試行回数です。
全てのアクションに対して決まった回数シミュレーションしないといけないのは、アクションが少しでも増えると現実的ではなくなります。
そこでアクションの選択に多腕バンディット問題を適用し、良い結果になるアクションを優先してシミュレーションさせることを考えます。
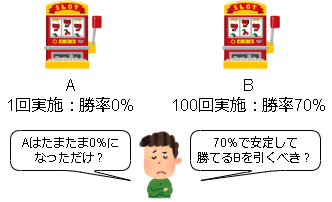
多腕バンディット問題(Multi-armed bandit problem)
知識の獲得(exploration:探索)と知識の利用(exploitation:活用)のジレンマを定式化した問題です。
例えばモンテカルロ探索で勝率の精度を上げるには探索回数を増やす必要があります。(知識の獲得)
しかし、探索回数を増やすとその分負ける手も多く指してしまうので実際の勝率は下がってしまいます。(知識の利用)
このトレードオフを表した問題になります。
元ネタのスロットマシーンで例えると以下みたいな感じです。
参考
・多腕バンディット問題(Wikipedia)
いつの間にか日本語のwikipediaができていますね
・Vol.31.No.5(2016/9)多腕バンディット問題 – 人工知能学会 (The Japanese Society for Artificial Intelligence)
UCT(UCB applied to trees)
多腕バンディット問題を解く有名なアルゴリズムにUCB(Upper Confidence Bounds)12があり、これをモンテカルロ探索に応用したのがUCTになります。
UCBの基本形は以下です。
I = argmax_{a \in A} \Big( \bar{X}_a + c_a \Big)
$a$ が選択肢で今回ですとアクションです。
$\bar{X}$ が平均報酬(勝率)、$c$ がペナルティ項で選択回数の多さに対してペナルティを与えます。
$\bar{X} + c$ が最大のアクションを選ぶ事でバランスよくアクションを選ぶ手法がUCBです。
ペナルティ項を含めた具体的なUCTの式は以下です。
$$
UCT_a = \frac{w_a}{n_a} + c \sqrt{ \frac{ \ln{N} }{n_a} }
$$
左項は勝率を表し、$w_a$ が勝利回数、$n_a$が試行回数です。
右項はペナルティを表し、$c$が定数、$N$が累計試行回数です。
(注意点として、各アクションは1回は選ばれてる必要があります。ですので $n_a>0$ を満たす必要があります。)
また、$c$ は探索パラメータで理論的には $\sqrt{2}$ になるようです。($c=\sqrt{2}$にするとUCB1になります)
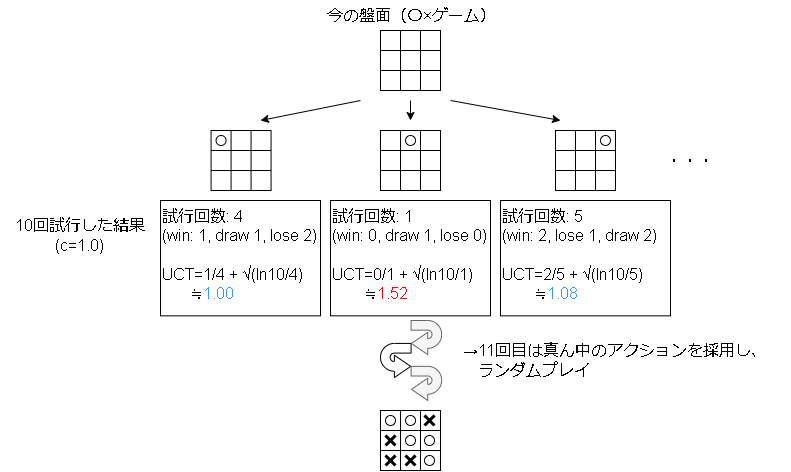
UCTでアクションを決める具体例は以下です。
図のようにUCT値で有望なアクションを優先的に探索する事で、シミュレーション回数を減らしています。
また、UCB1は試行回数が十分な場合、最善手の試行回数が最大となることが理論的に保証されているようです。3
参考
・Bandit based Monte-Carlo Planning (2006)
・Monte Carlo tree search(英Wikipedia)
モンテカルロ木探索(Monte Carlo tree search; MCTS)
モンテカルロ探索のその他の問題として、シミュレーションが完全にランダムでプレイされているという問題もあります。
これは言い換えると1手先しか読んでいない事と同義です。
そこで、オセロなどの一般的なAIに搭載されているようなN手先を読むアルゴリズムを実装することを考えます。
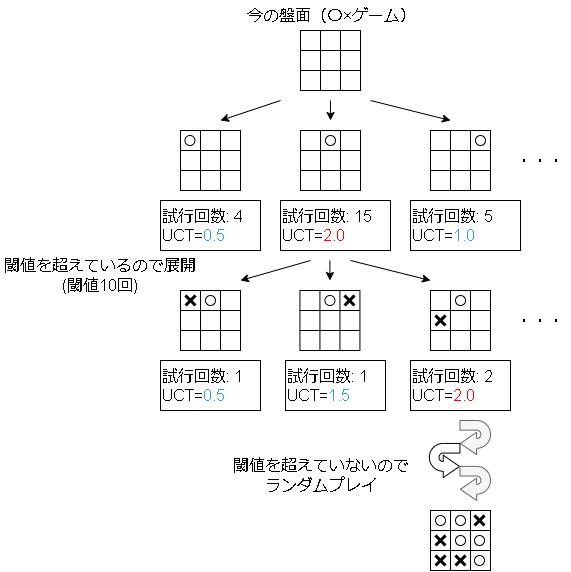
手の先読みですが、ある一定回数実行されたアクションの子ノードを展開する事で実現します。
試行回数が多いアクションは有望なアクションなのでそのアクションを展開する事で、先読みの実現と無駄な手の先読みを減らしています。
実装
フレームワーク上では二人零和有限確定完全情報ゲームではなく、マルコフ過程のモデルを前提に実装します。
具体的には勝率を行動価値に置き換え、結果の反映を割引報酬で実現します。
(割引率を1.0にすれば勝率と同じ結果になります)
また、MCTSは都度手を探索するので、学習というフェーズがありません。
フレームワーク的には学習時はシミュレーションを実施し、本番ではシミュレーションを実施せずに学習時の履歴だけでアクションを選ぶようにしています。
フレームワーク上の実装はgithubを見てください。
(関係のある箇所のみを抜粋しています)
Config
ハイパーパラメータです。
@dataclass
class Config(DiscreteActionConfig):
simulation_times: int = 10 # 1stepで実行するシミュレーション回数
expansion_threshold: int = 5 # 展開する閾値
gamma: float = 1.0 # 割引率
uct_c: float = np.sqrt(2.0) # UCTの探索パラメータ
Parameter
訪問履歴と報酬をテーブルで管理しています。
class Parameter(RLParameter):
def __init__(self, *args):
self.N = {} # 訪問回数
self.W = {} # 累計報酬
# 新しい状態の初期化
# self.config.action_num に環境側の取りうるアクション数が入っています
def init_state(self, state):
if state not in self.N:
self.W[state] = [0 for _ in range(self.config.action_num)]
self.N[state] = [0 for _ in range(self.config.action_num)]
Trainer
学習部分ですが、MCTSでは学習しないので使いません。
ただフレームワークの仕組み上、分散学習では遠隔でパラメータを保存しないといけないので、そのためのコードを書いています。
class Trainer(RLTrainer):
def train(self):
# メモリーに経験が来たらパラメータを更新する
batchs = self.remote_memory.sample()
for batch in batchs:
state = batch["state"]
action = batch["action"]
reward = batch["reward"]
self.parameter.init_state(state)
self.parameter.N[state][action] += 1
self.parameter.W[state][action] += reward
self.train_count += 1
return {}
Worker
メイン部分です。
学習時はアクションを決める際にシミュレーションします。
class Worker(ModelBaseWorker):
def call_policy(self, _state: np.ndarray, env: EnvRun, worker: WorkerRun) -> int:
state = to_str_observation(_state)
invalid_actions = self.get_invalid_actions(env)
self.parameter.init_state(state)
# トレーニングではシミュレーションする
# 環境は変えないようにバックアップ・リストアする
if self.training:
dat = env.backup()
for _ in range(self.config.simulation_times):
self._simulation(env, state, invalid_actions)
env.restore(dat)
# 試行回数のもっとも多いアクションを採用
c = self.parameter.N[self.state]
c = [-np.inf if a in invalid_actions else c[a] for a in range(self.config.action_num)] # mask
action = int(random.choice(np.where(c == np.max(c))[0]))
return action
# 1stepシミュレーションする(再帰)
# envのplayer手番の報酬を返す
def _simulation(self, env: EnvRun, state: str, invalid_actions, depth: int = 0):
if depth >= env.max_episode_steps: # for safety
return 0
# 今のプレイヤーを保存
player_index = env.next_player_index
# actionを選択
uct_list = self._calc_uct(state, invalid_actions)
action = random.choice(np.where(uct_list == np.max(uct_list))[0])
if self.parameter.N[state][action] < self.config.expansion_threshold:
# アクション回数がすくないのでロールアウト
reward = self._rollout(env, player_index)
else:
# 1step実行
env.step(action)
reward = env.step_rewards[player_index]
if env.done:
pass # 終了
else:
n_state = to_str_observation(env.state)
n_invalid_actions = env.get_invalid_actions()
enemy_turn = player_index != env.next_player_index
# expansion
n_reward = self._simulation(env, n_state, n_invalid_actions)
# 前のプレイヤーの番と次のプレイヤーの番が違う場合、
# expansionは相手側の報酬が返ってくる。
# 相手側の報酬は最小になってほしいので-をかける
if enemy_turn:
n_reward = -n_reward
# 割引報酬
reward = reward + self.config.gamma * n_reward
self.parameter.N[state][action] += 1
self.parameter.W[state][action] += reward
# 分散学習はremote_memoryに送る
if self.distributed:
self.remote_memory.add(
{
"state": state,
"action": action,
"reward": reward,
}
)
return reward
def _calc_uct(self, state, invalid_actions):
self.parameter.init_state(state)
# 各アクションのUCT値を計算
N = np.sum(self.parameter.N[state])
uct_list = []
for a in range(self.config.action_num):
if a in invalid_actions:
uct = -np.inf
else:
n = self.parameter.N[state][a]
if n == 0: # 1度は選んでほしい
uct = np.inf
else:
# UCT値を計算
q = self.parameter.W[state][a] / n
cost = self.config.uct_c * np.sqrt(np.log(N) / n)
uct = q + cost
uct_list.append(uct)
return uct_list
# ロールアウト
# ランダムプレイし、player_index 側の報酬を割り引いて返す
def _rollout(self, env: EnvRun, player_index):
done = False
rewards = []
while not done:
env.step(env.sample())
rewards.append(env.step_rewards[player_index])
done = env.done
# 割引報酬
reward = 0
for r in reversed(rewards):
reward = r + self.config.gamma * reward
return reward
学習結果
コードは以下です。
OXゲームを学習させてみました。
学習コードは github を参照してください。
CPUはデフォルトの"random"と"cpu"を用意してあります。
"cpu"は必ず最善手を打つアルゴリズムです。
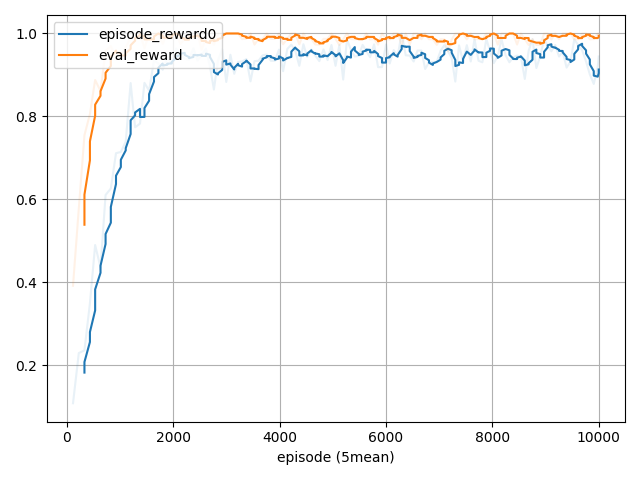
学習過程
対戦相手は "random" なのでほぼ100%勝てるようになっていますね。
各CPUとの対戦結果
Average reward for 100 episodes: [ 0.98 -0.98], [None, 'random']
Average reward for 100 episodes: [-0.94 0.94], ['random', None]
Average reward for 100 episodes: [0. 0.], [None, 'cpu']
Average reward for 100 episodes: [0. 0.], ['cpu', None]
OXゲームは最善手を打つと先行後攻どちらも引き分けになります。
ランダムは問題なく勝ててます。
"cpu"ではちゃんと引き分けていますね。
1エピソードの結果
### 0
----------
| 0| 1| 2|
----------
| 3| 4| 5|
----------
| 6| 7| 8|
----------
next player: O
0 : 0.0643( 6373), uct 0.12265
1 : 0.0565( 4955), uct 0.12264
2 : 0.0397( 3150), uct 0.12263
3 : 0.0464( 3729), uct 0.12263
*4 : 0.0877( 17781), uct 0.12264
5 : 0.0507( 4184), uct 0.12264
6 : 0.0416( 3297), uct 0.12263
7 : 0.0481( 3905), uct 0.12264
8 : 0.0429( 3406), uct 0.12263
### 1, action 4, rewards [0 0], done False(), next 1
----------
| 0| 1| 2|
----------
| 3| o| 5|
----------
| 6| 7| 8|
----------
next player: X
env_info : {}
work_info 0: None
train_info: None
- alphabeta(0, 0.001s) -
----------
| 0|-1| 0|
----------
|-1|-9|-1|
----------
| 0|-1| 0|
----------
### 2, action 0, rewards [0 0], done False(), next 0
----------
| x| 1| 2|
----------
| 3| o| 5|
----------
| 6| 7| 8|
----------
next player: O
env_info : {}
work_info 1: None
train_info: None
x 0 : 0.0000( 0), uct -inf
1 : 0.0440( 5405), uct 0.10546
2 : 0.0224( 2953), uct 0.10545
*3 : 0.0515( 6996), uct 0.10545
x 4 : 0.0000( 0), uct -inf
5 : 0.0180( 2667), uct 0.10544
6 : 0.0198( 2779), uct 0.10546
7 : 0.0183( 2683), uct 0.10545
8 : 0.0273( 3337), uct 0.10545
### 3, action 3, rewards [0 0], done False(), next 1
----------
| x| 1| 2|
----------
| o| o| 5|
----------
| 6| 7| 8|
----------
next player: X
env_info : {}
work_info 0: {}
train_info: None
- alphabeta(0, 0.000s) -
----------
|-9|-1|-1|
----------
|-9|-9| 0|
----------
|-1|-1|-1|
----------
### 4, action 5, rewards [0 0], done False(), next 0
----------
| x| 1| 2|
----------
| o| o| x|
----------
| 6| 7| 8|
----------
next player: O
env_info : {}
work_info 1: {}
train_info: None
x 0 : 0.0000( 0), uct -inf
*1 : 0.0328( 2590), uct 0.11634
2 : 0.0288( 2359), uct 0.11634
x 3 : 0.0000( 0), uct -inf
x 4 : 0.0000( 0), uct -inf
x 5 : 0.0000( 0), uct -inf
6 : -0.4219( 64), uct 0.10942
7 : 0.0247( 2149), uct 0.11635
8 : -0.0058( 1212), uct 0.11631
### 5, action 1, rewards [0 0], done False(), next 1
----------
| x| o| 2|
----------
| o| o| x|
----------
| 6| 7| 8|
----------
next player: X
env_info : {}
work_info 0: {}
train_info: None
- alphabeta(0, 0.001s) -
----------
|-9|-9|-1|
----------
|-9|-9|-9|
----------
|-1| 0|-1|
----------
### 6, action 7, rewards [0 0], done False(), next 0
----------
| x| o| 2|
----------
| o| o| x|
----------
| 6| x| 8|
----------
next player: O
env_info : {}
work_info 1: {}
train_info: None
x 0 : 0.0000( 0), uct -inf
x 1 : 0.0000( 0), uct -inf
*2 : 0.0099( 1712), uct 0.10943
x 3 : 0.0000( 0), uct -inf
x 4 : 0.0000( 0), uct -inf
x 5 : 0.0000( 0), uct -inf
6 : 0.0079( 1644), uct 0.10944
x 7 : 0.0000( 0), uct -inf
8 : 0.0007( 1433), uct 0.10945
### 7, action 2, rewards [0 0], done False(), next 1
----------
| x| o| o|
----------
| o| o| x|
----------
| 6| x| 8|
----------
next player: X
env_info : {}
work_info 0: {}
train_info: None
- alphabeta(0, 0.000s) -
----------
|-9|-9|-9|
----------
|-9|-9|-9|
----------
| 0|-9|-1|
----------
### 8, action 6, rewards [0 0], done False(), next 0
----------
| x| o| o|
----------
| o| o| x|
----------
| x| x| 8|
----------
next player: O
env_info : {}
work_info 1: {}
train_info: None
x 0 : 0.0000( 0), uct -inf
x 1 : 0.0000( 0), uct -inf
x 2 : 0.0000( 0), uct -inf
x 3 : 0.0000( 0), uct -inf
x 4 : 0.0000( 0), uct -inf
x 5 : 0.0000( 0), uct -inf
x 6 : 0.0000( 0), uct -inf
x 7 : 0.0000( 0), uct -inf
*8 : 0.0000( 4211), uct 0.06296
### 9, action 8, rewards [0 0], done True(env), next 0
----------
| x| o| o|
----------
| o| o| x|
----------
| x| x| o|
----------
next player: O
env_info : {}
work_info 0: {}
train_info: None
-
強化学習でいうところの価値です。モンテカルロ木探索はオセロや将棋などの二人零和有限確定完全情報ゲームを想定しているので勝率としています。 ↩
-
1って何だろうと思っていましたが、論文にUCB1 (see Theorem 1),UCB2 (see Theorem 2)と2つのUCBが書かれているので1つ目をさしているっぽいです。 ↩
-
Finite-time Analysis of the Multiarmed Bandit Problem (Peter Auer, Nicolò Cesa-Bianchi & Paul Fischer Machine Learning volume 47, pages235–256 (2002)) ↩