LoginSignup
8
8

More than 3 years have passed since last update.

天文学Advent Calendar 2019Day 7
@phyblas(雛星 φυβλας)

主成分分析（PCA）を使う、系外惑星探索

Last updated at Posted at 2019-10-10

はじめに

この前の記事では直接撮像法による系外惑星探索について説明しました
https://qiita.com/phyblas/items/52dc1bd113aff3745a8d

今回は、機械学習の方法の一つである主成分分析（principle component analysis、PCA）を加えて、もっと系外惑星をはっきり見える方法について説明します。

主成分分析（PCA）とは

主成分分析（PCA）の基本については色んな記事で説明してあるので省略します。

理論や簡単な使い方はこの記事を参考に
- https://qiita.com/NoriakiOshita/items/460247bb57c22973a5f0
- https://qiita.com/Hatomugi/items/d6c8bb1a049d3a84feaa

PCAは画像処理に使かわれることも多いです。これについてこの記事の説明がいいです。
- https://qiita.com/kenmatsu4/items/c61ce5d85667f499c3c8
- https://qiita.com/supersaiakujin/items/138c0d8e6511735f1f45

今回は天文写真の処理に使うことになります。

PCAを使う前に標準偏差で割る場合が多いが、画像処理にとっては普通は必要ないのです。

これについてこの記事参照
https://qiita.com/koshian2/items/2e69cb4981ae8fbd3bda

PCAを使うには普通はsklearnのsklearn.decomposition.PCAを使うことが便利ですが、実際にその中のPCAの計算は特異値分解（singular value decomposition、SVD）で行われます。

PCAとSVDの関係についてはこの記事の説明がいいです。 https://qiita.com/horiem/items/71380db4b659fb9307b4

ここでsklearnを使わずに直接scipyでSVDの計算をします。

SVDを計算する方法は色々あり、例えば
- numpy.linalg.svd
- scipy.linalg.svd
- scipy.sparse.linalg.svds

データサイズが大きい場合、scipy.sparse.linalg.svdsを使う方がずっと早いので、今回もこれを使います。

使い方についてこの記事も参考に
https://qiita.com/mizunototori/items/38291518110849e91a4c

主成分分析を使うところ

この前の記事にも説明した通り、直接系外惑星の姿を撮りたい時、PSF（point spread function = 点拡がり関数）やスペックルノイズなどのノイズを消滅するために普段はADI（angular differential imaging = 角度差分撮像）という方法で何枚の写真を連続で撮影して後で合成するのです。

本来のADIの方法では、PSFはあまり時間によって変わらないと考えて、何枚の写真を合わせて中央値を求めてそれを全ての写真のPSFの値として扱って、そして全ての写真からひくと、PSFが消えて惑星の姿がはっきり見える。

こういう方法は簡単ですが、実際にPSFは時間と共に少しずつ変わっていくもので、その違いも考慮して、違う値でひいたらもっといい結果になるはずです。

ノイズのパターンを掴むことは重要なポイントです。

そのために色んな方法が提案されますが、その中でよく使われる方法はPCAを使うという方法です。

もともとADIという方法は2006年にマロワ（Marois）等によって提案されたものです。その後LOCIやANDROMEDAなどのADIの改善する方法も引き続き提案されました。

初めてADIにPCAを使ったのは2012年に別々に発表された2つの論文
- PYNPOINT: an image processing package for finding exoplanets, Amara & Sascha (2012)
- Detection and Characterization of Exoplanets and Disks Using Projections on Karhunen-Loève Eigenimages, Soummer et al. (2012)

これを皮切りにして、その後PCAはADIによく使われる方法になってきたのです。

ADIにPCAを加えるという方法はKLIP（Karhunen-Loève image projection、もしくはprocessing）と呼ばれることも多いです。

やり方

写真は二次元の明るさのデータで、違う時間で何枚も連続撮ったものだから、時間と空間を合わせたら三次元データになります。波長（あるいは、色）を分けたら四次元になるが、ここでは簡単のために一色の明るさを考慮します。

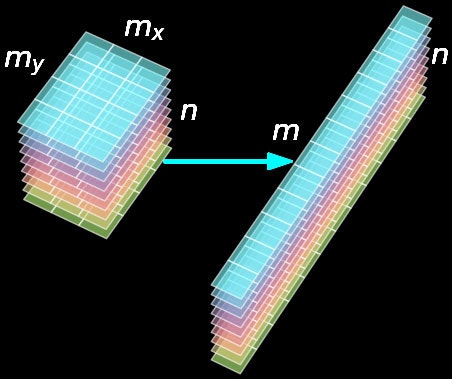
PCAでは普通は二次元（各データ×各特徴）配列を入力として使われるので、二次元の空間を一次元に変形する必要があります。

画像が広さ$m_x$、高さ$m_y$ピクセルで$n$枚あるとしたら、データは$n \times m_x\times m_y$の配列になりますが、ここでまずは1ピクセルは1つの特徴にします。$m = m_x \times m_y$ピクセルが$m$特徴にしたら、データは$n \times m$の配列になります。

このようなn行m列の行列に書けます。

Z = \begin{bmatrix}
z_{1,1} & z_{1,2} & \cdots & z_{1,m} \\ \\
z_{2,1} & z_{2,2} & \cdots & z_{2,m} \\ \\
\vdots & \vdots & \ddots & \vdots \\ \\
z_{n,1} & z_{n,2} & \cdots & z_{n,m} \\
\end{bmatrix}

$z_{i,j}$はi番目の画像のj番目のピクセルの明るさ。

各枚の画像の各ピクセルの明るさは、恒星のPSFやスペックルノイズや惑星など、色んな要因から成されるもので、色んな成分の足し合わせに見なすことができます。

このように分割できます。

\begin{align}
z_{i,j} = \sum_{h=1}^{m} \xi_{i,h} w_{h,j}
\end{align}

$\xi_{i,h}$は$i$番目の画像での$h$番目の成分の値。$w_{h,j}$は$j$番目ピクセルに対する$h$番目の成分の重み。

こうやってデータはこのように、かけ合った2つの行列に分解できます。

\begin{align}
  X_{[n\times m]} &=
  \Xi_{[n\times m]}W_{[m\times m]} \\
  \begin{bmatrix}
    z_{1,1} & z_{1,2} & \cdots & z_{1,m} \\ \\
    z_{2,1} & z_{2,2} & \cdots & z_{2,m} \\ \\
    \vdots & \vdots & \ddots & \vdots \\ \\
    z_{n,1} & z_{n,2} & \cdots & z_{n,m} \\
  \end{bmatrix} &=
  \begin{bmatrix}
    \xi_{1,1} & \xi_{1,2} & \cdots & \xi_{1,m} \\ \\
    \xi_{2,1} & \xi_{2,2} & \cdots & \xi_{2,m} \\ \\
    \vdots & \vdots & \ddots & \vdots \\ \\
    \xi_{n,1} & \xi_{n,2} & \cdots & \xi_{n,m} \\
  \end{bmatrix}
  \begin{bmatrix}
    w_{1,1} & w_{1,2} & \cdots & w_{1,m} \\ \\
    w_{2,1} & w_{2,2} & \cdots & w_{2,m} \\ \\
    \vdots & \vdots & \ddots & \vdots \\ \\
    w_{m,1} & w_{m,2} & \cdots & w_{m,m} \\
  \end{bmatrix}
\end{align}

ここで$W$は直交行列である重みの行列です。直交行列の性質で

\begin{align}
W^TW = W^{-1}W = I
\end{align}

それで

\begin{align}
Z &=& \Xi W \\
ZW^T &=& \Xi W W^T &=& \Xi \\
ZW^T W &=& \Xi W &=& X
\end{align}

これはつまり、$Z$は$W^T$でかけたら$\Xi$になり、そしてまた$W$でかけたら$Z$に戻るということです。

しかし、ここでの目的はPSFの影響をたくさん受ける成分を求めることです。PSFによるノイズは時間と共に変化していくといっても、何か固定な傾向がある変化です。そのような変化は主成分に捉えられやすいです。

PCAでは主成分は何か一定の変化の傾向を持っている説明能力の高い成分のことです。

つまり、その主成分は、PCAのノイズの影響をたくさん受ける成分だと考えることができます。その主成分を求めて、元のデータからひいたら、ノイズが大分消されて、惑星の姿は残されてはっきり見えるようになります。

説明能力が高い最初の$k$成分だけ取ったら、重みの行列は$k$行だけ残ります。

P = \begin{bmatrix}
w_{1,1} & w_{1,2} & \cdots & w_{1,m} \\ \\
w_{2,1} & w_{2,2} & \cdots & w_{2,m} \\ \\
\vdots & \vdots & \ddots & \vdots \\ \\
w_{k,1} & w_{k,2} & \cdots & w_{k,m} \\
\end{bmatrix}

ここで$P$は主成分ばかりの重みで、$k=m$の場合$P$は$W$となり、$P^TP=I$になりますが、$k<m$の場合は、これはつまりただ主成分だけ取って再構成するということになります。

Z_p = Z P^T P

$Z_p$は主成分だけ使って再構成されたデータの配列で、$i$番目の画像の$j$番目のピクセルの再構成された値は

\begin{align}
z_{p(i,j)} = z_{i,j}\sum_{h=1}^k w_{h,j}^2
\end{align}

元のデータ$Z$から$Z_p$をひいたら残るのは惑星と他のノイズです。（ガウス雑音のノイズは主成分に含まれることはないのでまだ残る）

ただ、主成分の数$k$はどれくらいでいいかは問題によって違うので、これも又よく考慮しなければならないハイパーパラメータです。

それともう一つの問題は、中心の部分が値のノイズが大きいため、PCAの計算に邪魔することが多いので、中心部が必要ない場合この部分を除外することでいい結果になることもあります。なので、これももう一つ考慮するかもしれないハイパーパラメータです。

実装

ここで流れを纏めると、

  • 中心の部分を除外
  • 画像データを二次元の$n$行$m$列の行列にする
  • 各枚の間の平均値を計算してそれをひいて、平均値を0にする
  • 主成分（最も説明能力の高い$k$成分）の重み行列$P$を求める
  • $ZP^TP$を計算して、それを元のデータからひく
  • 全ての画像を視差角によって回転し、最後に中央値を求める

次は実装。

使うデータはこの前の記事で使ったHR8799という星のデータにします。

その記事と同じ流れで生データの解析をしたら、HR8799_20150928/products/science_cube.fitsとscience_parang.fitsができます。

次の段階は、普通に中央値を取るという方法の代わりに、PCAを使います。

使っているSPHERE/IRDISは2つの波長がありますが、今回では0番目の波長（このHR8799_20150928のデータセットでは2110nm）だけを使います。

もっと詳しい説明はコードの中のコメントで

import matplotlib.pyplot as plt
import numpy as np
from astropy.io import fits
from skimage.transform import rotate
from scipy.sparse.linalg import svds
import os

rmin = 25 # 除外する中心部の半径
n_pc = 12 # 主成分の数

folder = 'HR8799_20150928/products'

# 解析が完了した画像データ
path_sc = os.path.join(folder,'science_cube.fits')
# データは四次元だが、一番目の次元は波長で、今回は短い方の波長 (0番目) だけ使う
z = fits.getdata(path_sc)[0,:,150:-150,150:-150]
# 視差角
path_parang = os.path.join(folder,'science_parang.fits')
parang = fits.getdata(path_parang)
z -= z.mean(0) # 平均值をひく
shape = z.shape
z = z.reshape(shape[0],-1) # 二次元の画像を一次元に変形する

xc,yc = (shape[2]-1)/2.,(shape[1]-1)/2. # 中心の位置
my,mx = np.indices([shape[1],shape[2]])
mx,my = mx.ravel()-xc,my.ravel()-yc
mr = np.sqrt(mx**2+my**2) # 中心からの距離
z[:,mr<rmin] = np.nan # 中心部を除外

p = svds(z[:,mr>=rmin],n_pc)[2] # 中心部以外だけを取ってSVDを実行して重み行列を求める
z[:,mr>=rmin] -= z[:,mr>=rmin].dot(p.T).dot(p) # 主成分だけでデータ再構成
z = z.reshape(shape) # データ形を二次元の画像に戻す

# 視差角による回転
for i,parang_i in enumerate(parang):
    z[i] = rotate(z[i],-parang_i,cval=np.nan)
# 中央値
res = np.median(z[:,100:-100,100:-100],0)

# 結果を描く
plt.figure(figsize=[6,5]).gca(facecolor='k')
plt.imshow(res,origin='bottom',cmap='PuBu_r')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.savefig('adi_pca%d.png'%n_pc)
plt.close()

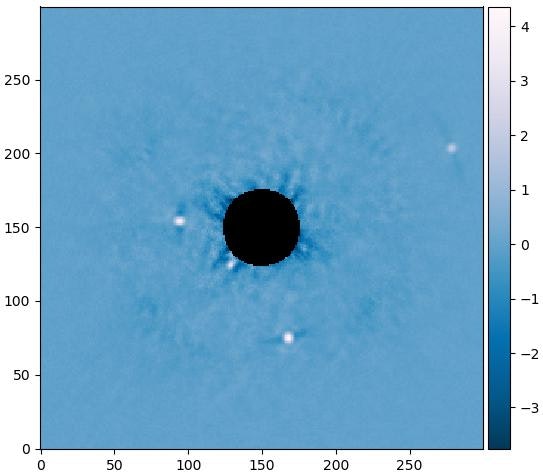
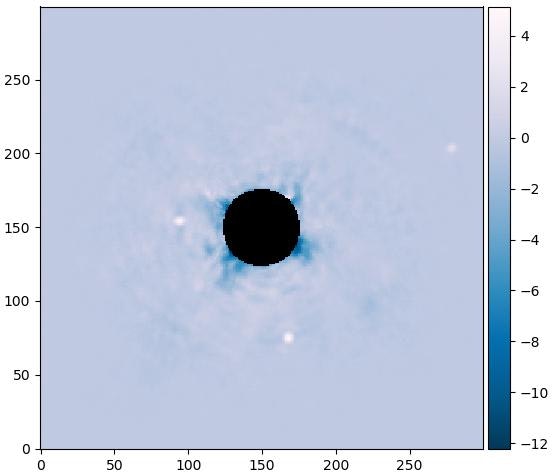
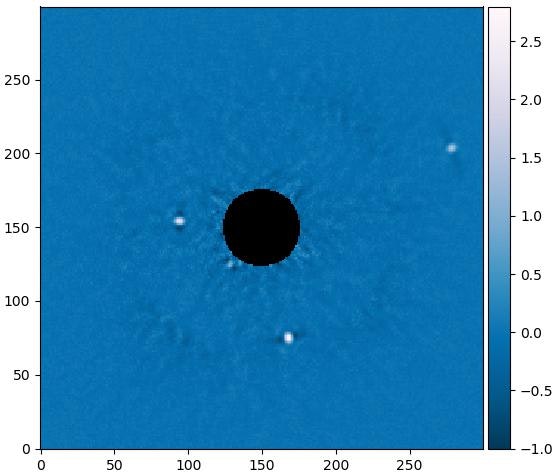
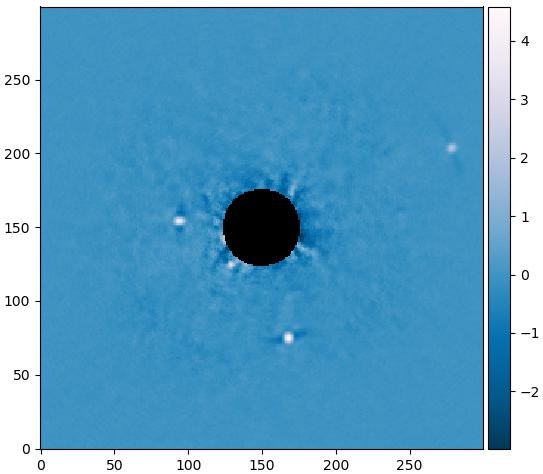
ここでは主成分の数が12で、このような結果ができます。

adi_pca12.jpg

ここから4つの明るい点が見えます。中心から一番遠いものから近いものまで並ぶと、HR8799b、HR8799c、HR8799d、HR8799e。

元の方法ではHR8799eを見ることが難しいが、今回でPCAを使ったらこのようにはっきり見えるようになりました。

主成分の数が変われば結果も大きく変わります。

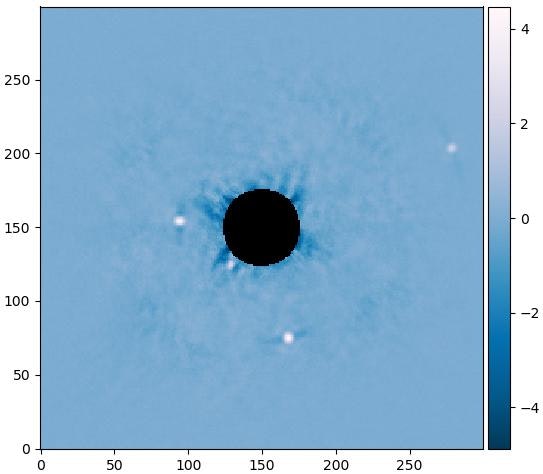
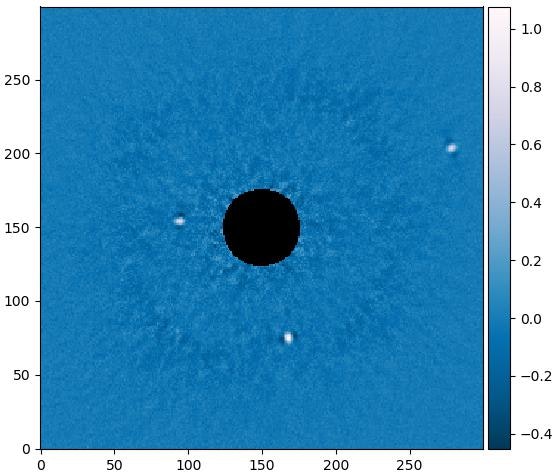
例えば8にする場合

adi_pca8.jpg

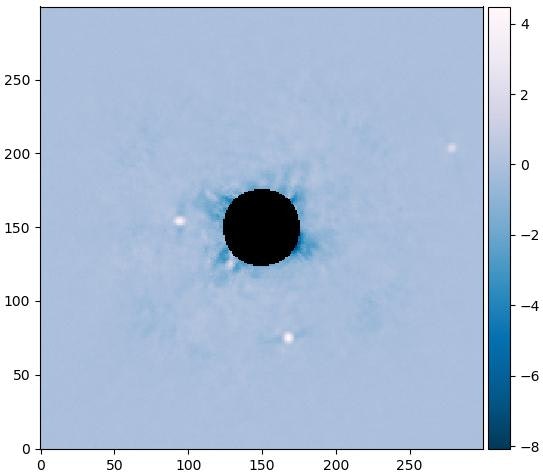
6

adi_pca6.jpg

4

adi_pca4.jpg

2

adi_pca2.jpg

主成分の数が少なすぎるとノイズがたくさん残って惑星は見えにくくなります。

逆に主成分が多すぎると、惑星の信号もたくさん主成分に含められて薄くなります。

例えば、50にする場合

adi_pca50.jpg

100

adi_pca100.jpg

こんな風にHR8799eの姿は随分薄くなってしまいます。

環状のPCA

PCAを使う時、計算の参考に使うデータと、後で結果を使って再構成するデータとは、必ずしも同じものであるわけではないのです。

上述の方法では、ただ簡単に全部のデータを参考に使って、そしてそのデータ自身の主成分で再構成したのです。

ADIでの惑星探しでは、惑星の影響が主成分に巻き込まれることがあります。こうなったら残る惑星の信号が薄くなるので、できるだけ避けるべきことです。

そのため、n番目の画像の主成分を求める時にPCAの計算にn番目の画像と、近い視差角を持つ画像を参考データに含めないようにするという方法も提案されたのです。

2つの写真のフレームの視差角が近いというのはその写真の中での惑星の位置が近くにあるということです。なので視差角が目標のフレームから惑星の範囲より大きく離れるフレームだけ使う方が無難です。

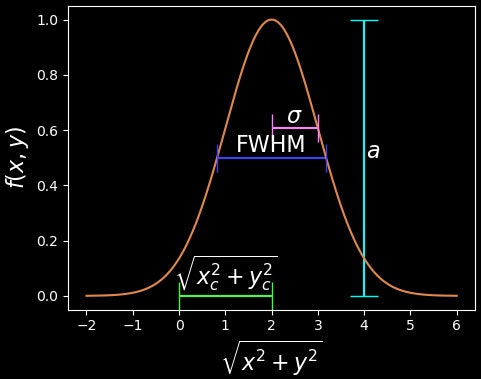
ここで惑星の範囲というのは、惑星が画像に写っている範囲です。実際に惑星もPSFによってエアリーディスクの姿になりますが、簡単に二次元ガウス関数に見なすこともできます。

f(x,y) = a\exp{\left(-\frac{(x-x_c)^2+(y-y_c)^2}{2\sigma^2}\right)}

普通は半値全幅（FWHM）が惑星の範囲を示すのによく使われます。

ガウス関数のFWHMと$\sigma$との関係は

\mathrm{FWHM} = 2\sqrt{2\ln 2}\sigma \approx 2.355\sigma

SPHEREデータでは、products/psf_cube.fitsにある解析されたOBJECT,FLUXのデータを使ったら、PSFの様子とFWHMを求めることができますが、今回は便宜上、FWHM=5ピクセルにします。（SPHEREデータのFWHMは大体が4~5ピクセルくらいだから大きく間違わない）

ただ、惑星の移動は中心に近いほど大きくなるものなので、除外するべきフレームは中心からの距離によって違います。

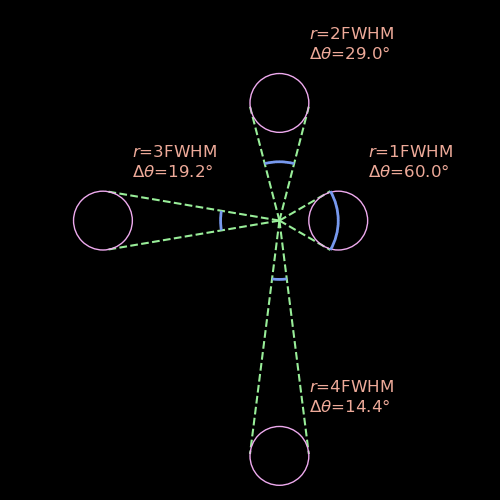
距離と角度の関係はこの画像通りです。

ここで$r$は中心からの距離で、$\Delta \theta$はFWHM内の角度の範囲です。こうやって計算できます。

\begin{align}
\Delta\theta > 2\arcsin\left(\frac{FWHM}{2r}\right)
\end{align}

だからいくつかの円環（アニュラス、annulus）に分けて別々にPCAの計算を行うということになります。

このように円環一つずつ取って別々に計算します。

次はpythonで実装。コードは随分複雑になるし、かかる時間も何倍も長くなります。詳しくはコートの中のコメントで

import matplotlib.pyplot as plt
import numpy as np
from astropy.io import fits
from skimage.transform import rotate
from scipy.sparse.linalg import svds
import os,time
t0 = time.time()

fwhm = 5
d_ann = 4 # 円環の広さ
rmin = 25 # 除外する中心部の半径
n_pc = 12 # 主成分の数

folder = 'HR8799_20150928/products'
path_sc = os.path.join(folder,'science_cube.fits')
path_parang = os.path.join(folder,'science_parang.fits')

z = fits.getdata(path_sc)[0,:,150:-150,150:-150]
parang = fits.getdata(path_parang)
n_f = len(z)

z -= z.mean(0) # 平均値をひく
shape = z.shape
z = z.reshape(shape[0],-1) # 二次元の配列に変形する

xc,yc = (shape[2]-1)/2.,(shape[1]-1)/2. # 中心の位置
rmax = int(min(xc,yc))
my,mx = np.indices([shape[1],shape[2]])
mx,my = mx.ravel()-xc,my.ravel()-yc
mr = np.sqrt(mx**2+my**2) # 中心からの距離
n_ann = int((rmax-rmin)/d_ann) # 円環の数
print('円環の数: %d'%n_ann)

r_ann_io = np.linspace(rmin,rmax,n_ann+1)
r_ann_out = r_ann_io[1:] # 円環の最も外
r_ann_in = r_ann_io[:-1] # 円環の最も中
r_ann_cen = (r_ann_in+r_ann_out)/2. # 円環の半ば
dthetamin = 2*np.degrees(np.arctan(fwhm*0.5/r_ann_cen)) # 使える最天元の視差角
zp = np.full_like(z,np.nan)
d_parang = np.abs(parang-parang[:,None]) # 視差角の差

# 円環一つずつ
for i_ann in range(n_ann):
    # 視差角が十分大きいかどうかを示すブールの配列
    dthetafar = d_parang>dthetamin[i_ann]
    # この円環の範囲にあるピクセルだけ取る
    in_xy_a = (r_ann_in[i_ann]<=mr)&(mr<r_ann_out[i_ann])
    z_i = z[:,in_xy_a]
    # 1フレームずつ主成分分析を行う
    for i_f in range(n_f):
        w = svds(z_i[dthetafar[i_f]],n_pc)[2]
        # その円環とそのフレームの主成分での再構成
        zp[i_f,in_xy_a] = z_i[i_f].dot(w.T).dot(w)
    print('%d番目完成。%.2f分経過'%(i_ann+1,(time.time()-t0)/60))

z -= zp # 主成分で再構成された値をひく
z = z.reshape(shape) # 形をもとに戻す
# 視差角による回転
for i,parang_i in enumerate(parang):
    z[i] = rotate(z[i],-parang_i,cval=np.nan)
res = np.median(z[:,100:-100,100:-100],0) # 中央値

# 結果を描く
plt.figure(figsize=[6,5]).gca(facecolor='k')
plt.imshow(res,origin='bottom',cmap='PuBu_r')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.savefig('adi_pca%d_ann.png'%n_pc)
plt.close()

結果

adi_pca12_ann.jpg

すでにあるpythonモジュール

PCAはよくADIに使われる方法なので、簡単に実装できるpythonモジュールがあります。

終わりに

以上は系外惑星探索におけるPCAの用途の一つです。

最近機械学習の方法が系外惑星探索を含めて色んな分野によく使われています。

PCAの他にのにNMFなどの方法もADIに使われることがあります。

8
8
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
8