Go to Qiita Advent Calendar 2024 Top
LoginSignup
232
205

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@koshian2(koshian2 ＠新刊通販中)

主成分分析で標準偏差で割るべき？に対する議論

Last updated at Posted at 2018-11-02

TL;DR

  • 主成分分析で標準化（標準偏差で割る）するのが必ずしもいいとは限らない
  • それどころか標準偏差で割ることの悪影響もある
  • 標準化すべきかどうかは、どこで主成分分析を使うか（可視化として使うのか、パイプラインとして使うのか）によっても異なるからそこをちゃんと考えましょう

主成分分析にも標準偏差で割る例と割らない例がある

「主成分分析をする際には標準化（正規化）をしましょう」と言われることはよくありますが、実はよく探すと割っている例と割っていない例があります。どちらで説明しているかは学者の間でも意見が分かれているようです。主成分分析を実行する前の変数変換を、

ケース1：平均だけ引く　$X-\mu$
ケース2：平均で引いて標準偏差で割る　$\frac{X-\mu}{\sigma}$

とする2通りです。大学が出している資料を見てみましょう。ケース1はオタゴ大学が出しているPDF 12ページ目、「subtract mean」とだけ書いてあってdivide by standard deviationとは書いていません。

ケース2は皆さんご存知Andrew Ng先生のスタンフォード大学の講義資料　2ページ目。「Replace each $x_j^{(i)}$ with $x_j^{(i)} / \sigma_j$」とあり、標準偏差で割ることを示しています。
また、高崎経済大学が出しているPDF。これはとてもわかりやすい資料です。35ページ目に一般的なp次元のデータに対して主成分分析を行う場合「与えられたデータに対して標準化を行う」を行うとあり、30ページ目の例の解説で平均で引き標準偏差で割る操作を標準化としているので、ケース2と考えられるでしょう。

ケース1もケース2も考慮している例。おそらくこれが多数派なのではないでしょうか。カリフォルニア州立大学のページでは標準偏差で割らずに主成分分析した場合の問題点を示し、次のページで代替案として標準化したケースを出しています。
東京大学の講義資料の8ページ目では標準化について解説はしているものの、これには注意書きがあり、「主成分分析においては分散は１に揃えない場合も多い」とあります。
同志社大学のページでは本質的な説明があって、Rでの解説ですが「関数prcompには引数scaleがあり、データの標準化(データのスケールを統一)が必要なときはscale=TRUEを指定する。デフォルトにはscale=FALSEになっている。scale=TRUEにすると元のデータの相関行列を用いた主成分に等しい」とあります。

Numpyから作る主成分分析

ケース1とケース2のどちらが良いかを理解するには、SklearnでPCAを使えるだけではなく、主成分分析の裏で何をやっているかを知る必要があります。Numpyベースで理解しましょう。

主成分分析の数学的な理解は、主成分分析とは分散共分散行列を固有値分解（特異値分解）して、固有値と固有ベクトルを求めるものです。より直感的で意味的な理解は、データに対して分散を最も表現できる新しい軸を探すことです。つまりxyといった軸の（基底の）変換なんですね。

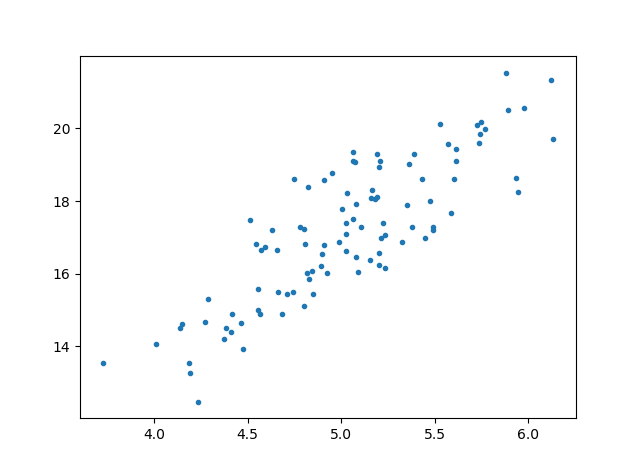
このようなサンプルデータを用意しました。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
X = np.random.randn(100, 1) * 0.5 + 5
y = X * 3 + 2 + np.random.randn(100, 1)
data = np.c_[X, y]

plt.plot(X, y, ".")
plt.show()

pca_sd_1.png

今データは平均で引き、標準偏差で割られているものとします。つまり先程のケース2とします。

data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)

主成分分析は以下のコードであらわされます。

主成分分析の中身
cov = np.cov(data, rowvar=False)
U, S, _ = np.linalg.svd(cov)

print(cov) # 分散共分散行列
print(U) # 固有ベクトル
print(S) # 固有値

後ほど確かめますが、特異値分解でやっても固有値分解（linalg.eig）でやってもどちらでもいいです1。特異値分解のほうがサポートしているフレームワークが多い気がするので特異値分解で書きました。

Scikit-learnのPCAでは、分散共分散行列、固有ベクトル、固有値にあたるパラメーターは以下のようにして求められます。

SklearnでのPCAの固有ベクトル、固有値
from sklearn.decomposition import PCA

pca = PCA()
pca.fit(data)

print("Sklearn : PCA")
print(pca.get_covariance()) # 分散共分散行列
print(pca.components_.T) # 固有ベクトル
print(pca.explained_variance_) # 固有値

分散共分散行列＝pca.get_covariance()、固有ベクトル＝pca.componets_の転置、固有値=pca.explained_variance_の対応になります。固有ベクトルがcomponents_の転置になることについてですが、Sklearn v0.20.0では$M=U\Sigma V^T$という特異値分解に対して、$U$ではなく$V^T$をexplained_varianceに割り当てているため（該当ソースコードはこちら）、pca.explained_variance_の結果を転置させるとSVDの結果とほぼ同じになるはずです。

結果を比較すると次の通りです。それぞれ、分散共分散行列、固有ベクトル、固有値の順です。正しく実装できているのが確認できます。

NumpyとSklearnの比較
Numpy : SVD
[[1.01010101 0.85394847]
 [0.85394847 1.01010101]]
[[-0.70710678 -0.70710678]
 [-0.70710678  0.70710678]]
[1.86404948 0.15615254]

Sklearn : PCA
[[1.01010101 0.85394847]
 [0.85394847 1.01010101]]
[[-0.70710678 -0.70710678]
 [-0.70710678  0.70710678]]
[1.86404948 0.15615254]

固有ベクトルの符号は反転することがある

ほぼ同じといったのは、プラスマイナスは反転することがあるということです。特異値分解の 固有ベクトルは新しい軸を探すものなので、符号が反転していても特に問題はありません。なぜなら、xy座標上で(-1, 0)でも(1, 0)でもどちらもx軸を指していることには変わりませんので。

もう少し詳しく書くと、一般に$M=U\Sigma V^T$という特異値分解においては、$\Sigma$は一意に定まっても、$U, V$は一意に定まらないことがあるそうです。詳しくはこちら。

ちなみに、一般のSVDでは$U$と$V$の次元は異なりますが、主成分分析では分散共分散行列が正方行列かつ対称行列（対称行列は正方行列の特別な場合なので、対称行列と言ったときは必ず正方行列です）という特殊な条件があるので、$U$と$V$が符号を除けばほぼ等しくなります。以下のコードで確かめられます。

正方行列と対称行列の比較
# 正方行列の場合
X = np.arange(9).reshape(3,3)
U, S, V = np.linalg.svd(X)
print(X)
print(U)
print(V.T) # 異なる、SVDで求めているのはV.Tであるのに注意
print()

# 対称行列の場合
X = np.array([[1,3,5],[3,2,4],[5,4,7]])
U, S, V = np.linalg.svd(X)
print(X)
print(U)
print(V.T) # ほぼ同じ
出力（対称行列の場合のみ、UとVの絶対値が等しくなる）
[[0 1 2]
 [3 4 5]
 [6 7 8]]
[[-0.13511895  0.90281571  0.40824829]
 [-0.49633514  0.29493179 -0.81649658]
 [-0.85755134 -0.31295213  0.40824829]]
[[-0.4663281  -0.78477477 -0.40824829]
 [-0.57099079 -0.08545673  0.81649658]
 [-0.67565348  0.61386131 -0.40824829]]

[[1 3 5]
 [3 2 4]
 [5 4 7]]
[[-0.46038935  0.88384959 -0.08277408]
 [-0.43679051 -0.30671769 -0.84565851]
 [-0.7728232  -0.35317724  0.52726667]]
[[-0.46038935 -0.88384959  0.08277408]
 [-0.43679051  0.30671769  0.84565851]
 [-0.7728232   0.35317724 -0.52726667]]

符号は異なってはいるものの、2つ目の対称行列の場合$U$と$V$はほぼ同じであるのが確認できます。1つ目のただ正方行列だった場合は、固有ベクトルの左側はかなりずれています。

そのため、主成分分析においてNumpyで作ったものとSklearnの組み込みを比較するときは、SVDの$U$と、Sklearnのpca.componets_の転置（内部的にはSVDの$M=U\Sigma V^T$の$V$）を同一のものと考えてよいということがわかります。

固有値と特異値の関係

ちなみにSVDは特異値分解ですが、いきなり「固有値、固有ベクトル」とあたかも固有値分解にと同じように言っている点についても確認しておきましょう。行列Mが対称行列の場合は、特異値と固有値が一致するという性質があります。主成分分析では分散共分散行列という対称行列に対して特異値分解・固有値分解をするためこう言えるのです。

少しそれを確認しましょう。

固有値と特異値の関係
import numpy as np
import matplotlib.pyplot as plt


def eigen_svd(matrix):
    print()
    print("★ 行列 ★")
    print(matrix)
    eigen_value, eigen_vector = np.linalg.eig(matrix)
    U, S, V = np.linalg.svd(matrix)
    print("固有値")
    print(eigen_value)
    print("SVDのS")
    print(S)
    print("固有ベクトル")
    print(eigen_vector)
    print("SVDのU")
    print(U)

# 正方行列の場合
X = np.arange(4).reshape(2,2)
eigen_svd(X)

# 対称行列の場合
X = np.array([[3,1],[1,2]])
eigen_svd(X)

2つ目のケースのみ対称行列です。対称行列の場合のみ、固有値と特異値が一致していることが確認できます。1つ目のケースでは固有値の絶対値が変わっているため、固有ベクトルも全く別のものになっています。

出力（対称行列のみ固有値と特異値が一致）
★ 行列 ★
[[0 1]
 [2 3]]
固有値
[-0.56155281  3.56155281]
SVDのS
[3.70245917 0.54018151]
固有ベクトル
[[-0.87192821 -0.27032301]
 [ 0.48963374 -0.96276969]]
SVDのU
[[-0.22975292 -0.97324899]
 [-0.97324899  0.22975292]]

★ 行列 ★
[[3 1]
 [1 2]]
固有値
[3.61803399 1.38196601]
SVDのS
[3.61803399 1.38196601]
固有ベクトル
[[ 0.85065081 -0.52573111]
 [ 0.52573111  0.85065081]]
SVDのU
[[-0.85065081 -0.52573111]
 [-0.52573111  0.85065081]]

ちなみにこの例（2つ目）では運良く固有値と特異値が一致しましたが、np.linalg.eigで求めた固有値と、np.linalg.svdで求めた特異値で符号が変わることがあります。おそらく実装の違いでしょうが、これらの関数が必要になったらどちらの関数を使うか統一したほうがいいかもしれません。

以下、np.linalg.svdの$S$を固有値、$U$を固有ベクトルとします。

平均で引くことの意味

冒頭のケース1でもケース2でも平均で事前に引いておきましたが、これは分散共分散行列を計算する都合によるものです。分散共分散行列の定義でこんな式を見たことはないでしょうか。

$$\rm{Cov}(X)=\frac{X^T X}{n-1} $$

転置の順序が逆になっていても構いません。この式はもう少し続きがあって、平均を引かない場合はこうなります。

$$\rm{Cov}(X)=\frac{X^T X}{n-1} - \mu^T\mu$$

ここで$\mu$は平均のベクトルです。平均を引いていた場合は$\mu$が全て0になるので、引き算の部分が省略できるというわけですね。確かに最初の式で分散共分散行列を求めるのなら平均で引く意味はあります。

ちなみに、分散共分散行列の値は平均を引こうが引かなかろうが変わりません。なぜなら共分散は平均で引いた値同士の積だからです。共分散の定義を思い出しましょう。

$$\rm{Cov}(x_i, x_j) = E[(x_i-\mu_{x_i})(x_j-\mu_{x_j})] = \frac{(x_i-\mu_{x_i})(x_j-\mu_{x_j})}{n-1}$$

「＝/(n-1)」としたのはnp.covが不偏分散で計算するためこれに合わせました。np.cov()のような関数で求める場合でも、平均を引く処理はやってくれます。また、平均の処理の有無は固有値と固有ベクトルに影響を与えません（標準偏差の処理は影響を与えます）。

平均で引くことと固有値、固有ベクトルの関係
np.random.seed(0)
X = np.random.randn(100, 1) * 0.5 + 5
y = X * 3 + 2 + np.random.randn(100, 1)
data = np.c_[X, y]

def view_eigen_vectors(data):
    cov = np.cov(data, rowvar=False)
    U, S, V = np.linalg.svd(cov)
    print(S) # 固有値
    print(U) # 固有ベクトル

mean = np.mean(data, axis=0, keepdims=True)

view_eigen_vectors(data)
print()
view_eigen_vectors(data-mean)
出力（平均で引いても引かなくても固有値と固有ベクトルは変わらない）
[3.92993728 0.06970263]
[[-0.21999051 -0.97550201]
 [-0.97550201  0.21999051]]

[3.92993728 0.06970263]
[[-0.21999051 -0.97550201]
 [-0.97550201  0.21999051]]

では平均で引くのが意味がないかというとそれは違います。平均を引く本当の意味とは、削減した次元に投射したり、削減した次元を戻したりするときにあります。もし、平均で引かない場合、Numpyでは以下のように書かないと正しい値を返しません。

平均で引かない場合のNumpyのPCA
def numpy_pca(data):
    cov = np.cov(data, rowvar=False)
    U, S, V = np.linalg.svd(cov)
    print("次元削減の固有ベクトル")
    U_reduce = U[:, :1]
    print(U_reduce)
    # 次元削減
    mean = np.mean(data, axis=0, keepdims=True)
    project = np.dot(data-mean, U_reduce)
    # 次元の復元
    data_rec = np.dot(project, U_reduce.T)+mean
    print("次元削減→復元")
    print(data_rec[:5, :])

from sklearn.decomposition import PCA
    
def sklearn_pca(data):
    pca = PCA(n_components=1)
    pca.fit(data)
    print("次元削減の固有ベクトル")
    print(pca.components_.T)
    # 次元削減
    project = pca.transform(data)
    # 次元の復元
    data_rec = pca.inverse_transform(project)
    print("次元削減→復元")
    print(data_rec[:5, :])

print("Numpy")
numpy_pca(data)
print()
print("Scikit-learn")
sklearn_pca(data)

numpy_pca()の次元の削減と復元の部分に注目。正直、次元を削減するときに平均を引いて、復元するときに平均を足したり面倒ですよね。こんなのバグの元です。最初から平均を引いて0にしてしまえば一発解決です。

Numpy
次元削減の固有ベクトル
[[-0.21999051]
 [-0.97550201]]
次元削減→復元
[[ 6.00626874 21.50121063]
 [ 4.84086798 16.3334842 ]
 [ 5.05769772 17.2949704 ]
 [ 5.97521052 21.36348945]
 [ 5.38621196 18.75169826]]

Scikit-learn
次元削減の固有ベクトル
[[-0.21999051]
 [-0.97550201]]
次元削減→復元
[[ 6.00626874 21.50121063]
 [ 4.84086798 16.3334842 ]
 [ 5.05769772 17.2949704 ]
 [ 5.97521052 21.36348945]
 [ 5.38621196 18.75169826]]

ちなみに固有ベクトルの符号は、削減→復元したときの値に左右しないようです。気になる方は確かめてみてください。

標準化する、しない場合でも一長一短

前置きが長くなってしまいましたが、主成分分析において、**「標準化する・しないによるメリット、デメリット」**を考えてみたいと思います。

標準化しないデメリット/標準化するメリット

これは明白です。そもそも変数のスケールが異なるので、同一のスケールで比較出ませんし、比較しようとするとミスリードを起こしやすくなります。

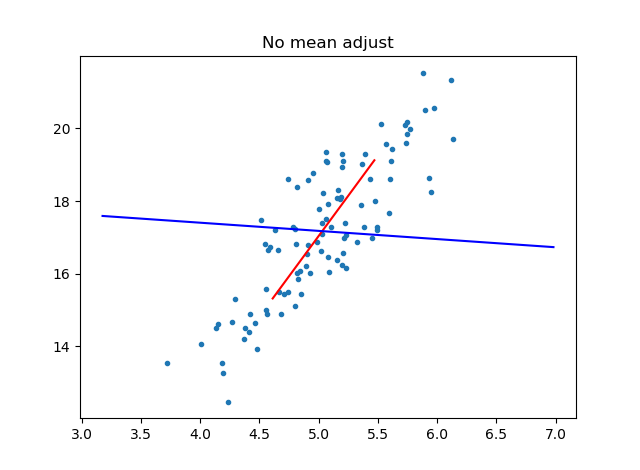
わかりやすいのは主成分軸です。平均で引かないケース、平均で引いたケース、平均で引いて標準偏差で引いた（標準化した）ケースで主成分分析を行い、主成分軸をプロットしてみました。

主成分軸をプロット
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
X = np.random.randn(100, 1) * 0.5 + 5
y = X * 3 + 2 + np.random.randn(100, 1)
data = np.c_[X, y]

def plot_principal_axis(data, title):
    cov = np.cov(data, rowvar=False)
    U, S, V = np.linalg.svd(cov)
    mean = np.mean(data, axis=0, keepdims=True)
    color = ["red", "blue"]
    plt.plot(data[:,0], data[:,1], ".")
    for i in range(len(S)):
        lines = np.dot(np.arange(-2.0,2.0,0.1).reshape(-1,1), U[:,i].reshape(1,-1)) + mean
        plt.plot(lines[:,0], lines[:,1], color=color[i])
    plt.title(title)
    plt.show()

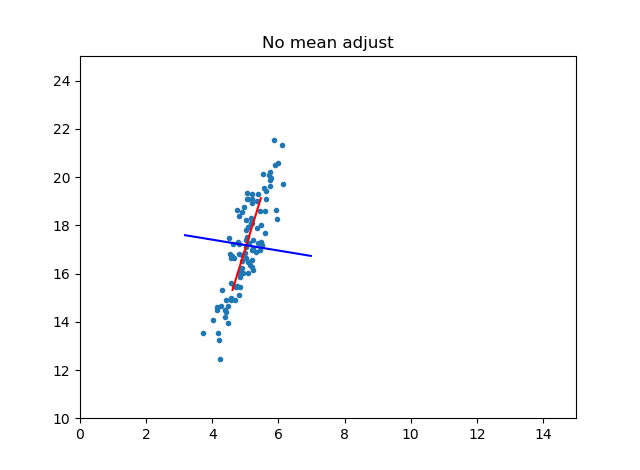
plot_principal_axis(data, "No mean adjust")

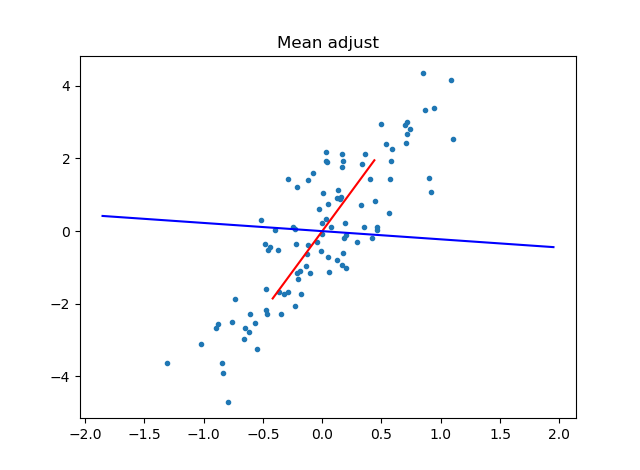
data_mean_adj = data - np.mean(data, axis=0, keepdims=True)
plot_principal_axis(data_mean_adj, "Mean adjust")

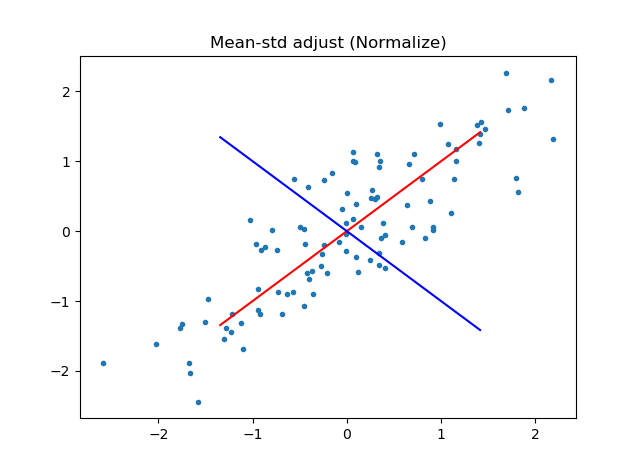
data_norm = data_mean_adj / np.std(data, axis=0, keepdims=True)
plot_principal_axis(data_norm, "Mean-std adjust (Normalize)")

上から、平均で引かないケース（No mean adjust）、平均で引いたケース（Mean adujust）、標準化したケース（Mean-std adjust(Normalize)）

pca_sd_2.png
pca_sd_3.png
pca_sd_4.png

標準偏差で割らない場合以外、軸がおかしい（直交していないように）見えますが、これはグラフの罠です。**全部のケースで軸は直交しています！**例えば一番最初のケースで、横軸を0～15、縦軸を10～25と幅を固定してみたらどうでしょうか？これはplot_principal_axisの関数のforループの中に次のようにコードを追加します。

        plt.plot(lines[:,0], lines[:,1], color=color[i])
        # 以下を追加
        plt.xlim((0,15))
        plt.ylim((10,25))

pca_sd_5.png

実はちゃんとスケールを直せば直交しているのです。もう少し定量的な解説をしましょう。これは高校数学の内容ですが、あるベクトル$\vec{a}, \vec{b}$の2つが直交するとき以下の式を満たします。

$$\vec{a}\cdot\vec{b} =0$$

2つのベクトルが直交するときその内積は0です。これをコードで検証してみましょう。

全てのケースで主成分軸が直交しているか
def check_orthogonal(data):
    cov = np.cov(data, rowvar=False)
    U, S, V = np.linalg.svd(cov)
    inner = np.dot(U[:,0], U[:,1])
    print(inner)

check_orthogonal(data)
check_orthogonal(data_mean_adj)
check_orthogonal(data_norm)

結果は以下の通りです。全てのケースで内積が0（誤差レベル）という結果になりました。つまり、平均で引こうが、標準偏差で割ろうが主成分軸は直交しているのです。

出力（全てのケースで内積≒0）
-3.3306690738754696e-16
3.608224830031759e-16
-5.551115123125783e-17

ちなみにこのような性質を持つ行列を直交行列と呼ぶそうです。もう少し詳しく書くと$M^TM=MM^T=E $($E$は単位行列)を満たす行列のこと2。直交行列は必ず正方行列（対称行列と似ていて、直交行列も正方行列の特別な場合です）なので、転置の順序を入れ替えても行列の大きさが変わることはありません。

そして、SVDで特異値分解するつまり$M=U\Sigma V^T$とするとき、$U, V$は直交行列になります。分散共分散行列は対称行列なので、SVDでの特異値と行列の固有値はほぼ同一とみなせます。したがって、固有ベクトルも直交行列になる、つまり主成分軸は必ず直交するという結論になります。

脱線してしまいましたが、標準化しない場合は以下のことが考えられます。

  • 標準偏差で割ろうが割らなかろうが、必ず主成分軸は直交している
  • しかし、グラフのスケールの都合上、標準偏差で割らない場合は軸のスケールがかわり、あたかも主成分軸が直交していないように見えることがある
  • 主成分分析はデータの可視化として重要な役割があるので、標準偏差で割らないままデータの分析をすると誤った結論が出ることがある

ここで1つ大事なことがわかりました。それは、主成分分析からグラフを含め、データの傾向や共通する要因（因子）を読み取りたい場合は、標準偏差で割るべきということです。これは抑えておきたいポイントです。

標準化するデメリット/標準化しないメリット

こちらは難しいです。いくつか例を挙げます。以前書いたPCA Color AugmentationというData Augmentationアルゴリズムがあります。

これは画像に対してカラーチャンネルあたりの主成分分析を行います。そこで求められた固有ベクトルに乱数をかけ、カラーチャンネルに値を加算するというものです。これにより1枚の画像から複数の画像ができ、あたかもデータが多数あるような正則化効果が得られます。

もう少し直感的に言うと、画像の色の分布に応じて足す量を決めましょうということです。例えば、赤が多い画像（例：夕焼け）なら、赤を多く足し他の色をあまり足さない、緑が多い画像（例：葉っぱ）なら、緑を多く足し他の色をあまり足さないなど。

例として夕日の画像を出しましょう。これをsunset.jpgとします。
sunset.jpg

まずはこれの色のヒストグラムを見てみます。

画像の色ヒストグラムを表示
from PIL import Image
import matplotlib.pyplot as plt
import numpy as np

img = np.asarray(Image.open("sunset.jpg").convert("RGB")).reshape(-1,3)
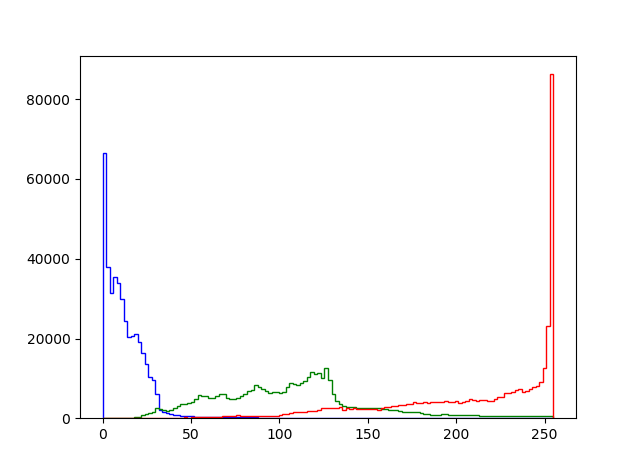
plt.hist(img, color=["red", "green", "blue"], histtype="step", bins=128)
plt.show()

見た目通り、赤が圧倒的に多くて、青はほとんどありませんね。緑がほどほどにという感じでしょうか。

pca_sd_6.png

カラーチャンネルあたりの分散共分散行列を確認しましょう。今、標準偏差では割りません。

カラーチャンネルあたりの分散共分散行列の確認
cov = np.cov(img, rowvar=False)
print(cov)
#[[2403.41386956 1724.76967548  211.41610039]
# [1724.76967548 1908.70599067  379.9284601 ]
# [ 211.41610039  379.9284601   204.43244419]]

R,G,Bのチャンネル順です。やはり、ヒストグラムで見たように赤の分散が一番大きく、ついで緑、青の分散は赤の分散の1/10未満ということになります。

しかし、これを標準偏差で割ってしまうと奇妙なことがおこります。平均でも引いて標準化していますが、今まで確認してきたように分散共分散行列に平均のシフトは寄与しません。

標準化した場合の分散共分散行列
img_normalized = (img - np.mean(img, axis=0, keepdims=True)) / np.std(img, axis=0, keepdims=True)
cov_noramlized = np.cov(img_normalized, rowvar=False)
print(cov_noramlized)
#[[1.00000242 0.80528268 0.3016129 ]
# [0.80528268 1.00000242 0.60821685]
# [0.3016129  0.60821685 1.00000242]]

なんと、赤と青の分散が同じ1と表現されてしまったのです。もともと赤の分散が青の分散の10倍以上あるのに、同一化されてしまうのは明らかにおかしいです。分散というのは重要な情報で、これは情報が落ちていると言わざるを得ません。

ちなみに標準化した場合の分散共分散行列は、冒頭の同志社大の先生が書いているように相関行列と同じです3。相関行列はnp.corrcoefで計算できます。

標準化したら相関行列と同じ
corr = np.corrcoef(img, rowvar=False)
print(corr)
#[[1.         0.80528073 0.30161217]
# [0.80528073 1.         0.60821538]
# [0.30161217 0.60821538 1.        ]]

つまり、標準化して主成分分析をする場合は、分散共分散行列＝相関行列となって、相関行列の固有ベクトルを求めていたということになります。

「情報が落ちる」という点について補足しましょう。主成分分析では特異値（≒固有値）を元に説明分散を計算しています。特異値の累積和を全体の和で4:割ると「pca.explained_variance_ratio_」に近い説明分散比を計算できます。

固有ベクトルあたりの説明分散比（標準化すると説明分散比が落ちる）
def explained_variance_ratio(data):
    cov = np.cov(data, rowvar=False)
    U, S, V = np.linalg.svd(cov)
    S_cumsum = np.cumsum(S)
    print(S_cumsum / np.sum(S))

explained_variance_ratio(img)
explained_variance_ratio(img_normalized)
#[0.87305681 0.97964698 1.        ]
#[0.72241881 0.95981481 1.        ]

標準化しない場合は固有ベクトル1つ取れば87%の分散を説明できたのに、標準化すると固有ベクトル1つでは72%の分散しか説明できなくなってしまいました。これは標準化したことで分散が均一化されてしまったことによる副作用と考えられないでしょうか。

ここで1つ補足しておきたいのは、標準化した後のPCAのほうが説明分散比が落ちた、つまり標準化すると主成分分析の精度が落ちるというわけではありません。そもそも標準化によって説明したい分散が変わっているのだから、標準化によって目標が変わっているわけです。この画像の例でいうと、標準化しないと赤と緑の画素を説明できればだいたい高得点（高い分散比）を出せるから、赤と緑を説明することに重点を置こう。ただし、標準化すると赤も緑も青も均一に説明しないといけないから、固有ベクトル1つ取っただけではなかなか高い分散比は出せないよ、と考えるのがわかりやすいと思います。目標が変わったので、分散比の意味合いが変わっているから精度は単純には比較できないよということでしょうか。

先程出したPCA Color Augmentationでも標準化による悪影響はあって、標準化すると本来はそこまでぶれないはずの青のチャンネルが赤のチャンネルと同じくらい動くという現象が確認できます。これは直感的におかしいですし、全体の色合いを損ねてしまう可能性があります。（上が標準化した例、下が標準化しない例です）
pca_sunset.gif

もう一つの例ですが、英語ですがこのQuoraの記事が秀逸で、例としてノイズから生成されたデータに対して標準化をして主成分分析をすると主成分軸がノイズ駆動になってしまうという悪例を挙げています。少し長いコードですが再現してみました。

import numpy as np
import matplotlib.pyplot as plt

def make_data():
    X = np.random.randn(100,2)
    X[:,0] = X[:,0] * 0.25 + 2.0
    return X

def calc_eigen_vectors(data):
    cov = np.cov(data, rowvar=False)
    U, S, V = np.linalg.svd(cov)
    mean = np.mean(data, axis=0, keepdims=True)
    return U, mean

def plot_principal_axis(data, ax, title):
    U, mean = calc_eigen_vectors(data)
    color = ["red", "blue"]
    ax.plot(data[:,0], data[:,1], ".")
    for i in range(U.shape[0]):
        lines = np.dot(np.arange(-2.0,2.0,0.1).reshape(-1,1), U[:,i].reshape(1,-1)) + mean
        ax.plot(lines[:,0], lines[:,1], color=color[i])
    plt.title(title)

def main():
    for i in range(20):
        data = make_data()
        plt.figure(figsize=(6,4))
        plt.subplots_adjust(left=0.1, right=0.9, top=0.9, bottom=0.1)

        ax = plt.subplot(1,2,1)
        plot_principal_axis(data, ax, "Disable normalize")
        normlize = (data - np.mean(data, axis=0, keepdims=True)) / np.std(data, axis=0, keepdims=True)
        ax = plt.subplot(1,2,2)
        plot_principal_axis(normlize, ax, "Enable normalize")
        plt.show()

if __name__ == "__main__":
    main()

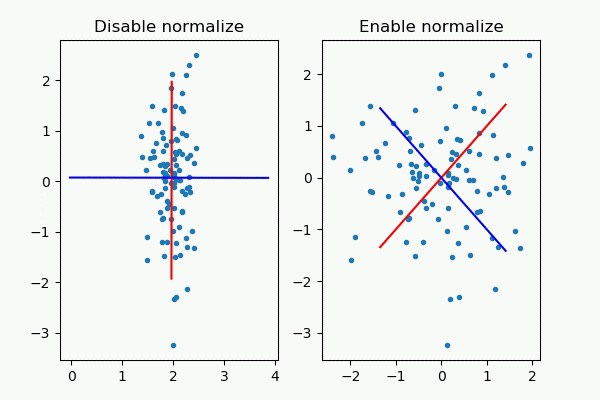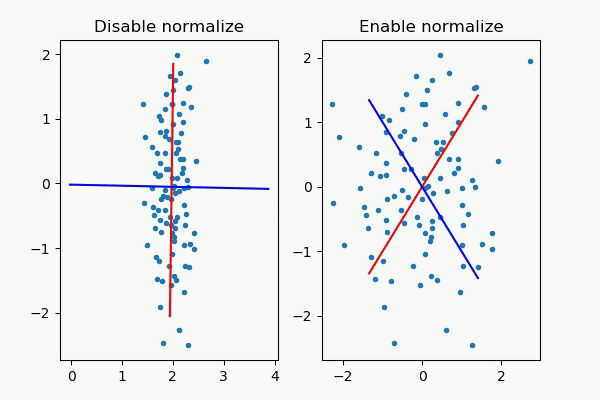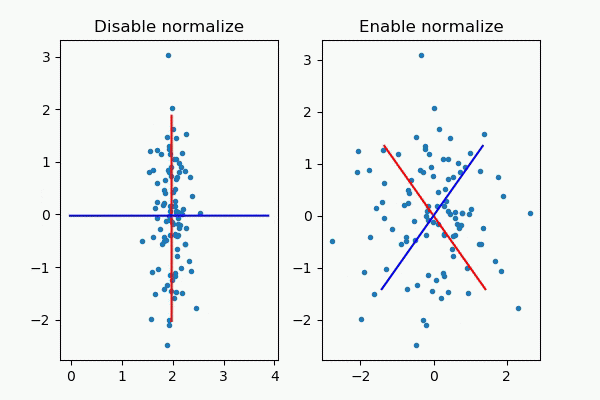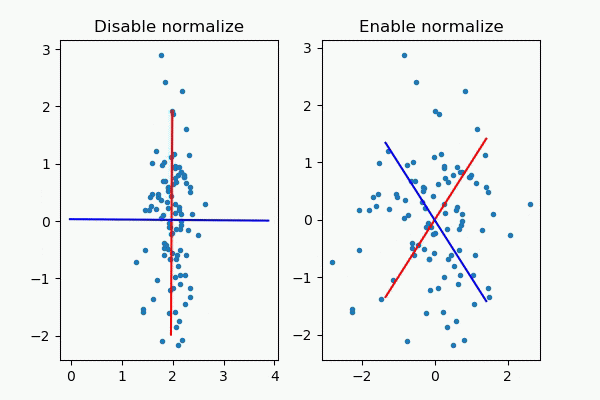
動画にまとめると次のようになります。

pca_sd_noise.gif

左側（標準化しない）場合はおおよそx軸とy軸が主成分軸として表示されていますが、右側（標準化）した場合は意味のない軸が表示されてしまいました。これは確かに困ります。

まとめるのが大変ですが、主成分分析で標準化すると困る例は次のようになると思います。

  • PCA Color Augmentationで夕日の画像のように、色の分布（分散）がRGBで全然違う例。主成分分析を可視化の目的ではなく、その後の機械学習のパイプラインにつなげるため目的、例えばData Augmentationで使うケース。
  • 可視化目的でもデータがほぼノイズから構成される特殊な例。標準化して出てきた主成分軸が全く意味をなさない場合。

まとめ

予想以上に長い投稿になってしまい、読んでいる方に負担をかけてしまいましたが、これまでの内容をまとめて、標準化のガイドラインを作ってみましょう。

  • 主成分分析には主に3つの使い方がある。1つ目はデータの可視化、これはとても強力で正しい使い方。2つ目は次元削減、ハードウェアの制約があって使うなら有効な使い方。3つ目はPCA Color Augmentationのように、次元削減でもないデータを水増しするための機械学習のパイプラインとして使うケース、これは例が少ないのでなんとも言えない。
  • 可視化目的だったら、基本的には標準化すべき。ノイズデータからなるような特殊な例もあるが、全体から見ればかなり珍しいので、異なるスケールで誤って比較した場合にミスリードする際のデメリットのほうが明らかに大きい。可視化だけではなく共通の要因を探るような場合も同様。ただ可視化する場合でもノイズデータのように、主成分軸が意味をなさなくなるケースはあるというのは頭の片隅に置いておくべき。
  • 次元削減の場合はなんとも言えない。可視化に近いような次元削減なら標準化したほうがいいし、パイプラインに近いような次元削減なら標準化しないほうが後続するパイプラインにより多くの情報を伝えられるかもしれない。標準化自体が1つのハイパーパラメーターなので、両方やって最終的に精度良いほうを取ればいい。
  • PCA Color Augmentationのようにパイプラインとして使うのなら、まず標準化しない路線で考えたほうがよいのではないか。
  • 標準化とは異なるスケールを相対的なスケールに変換し、同一のスケールで評価できるようにすることなので、同一のスケールで評価すべきか、あるいは別にスケール揃える必要がないのかで考えると理解しやすいかもしれない。

ここまでとても長い記事を読んでくださってありがとうございました。この手の専門家でもなんでもないので、強い方のご意見をお待ちしております。

  1. 固有値分解でも特異値分解でも固有ベクトル、固有値は求められます。詳しくはこちら　https://qiita.com/horiem/items/71380db4b659fb9307b4 ↩

  2. https://ja.wikipedia.org/wiki/%E7%9B%B4%E4%BA%A4%E8%A1%8C%E5%88%97 ↩

  3. グラム行列から見た分散共分散行列、相関行列の関係はこちらに書きました　https://blog.shikoan.com/cov-corr-gram-matrix/ ↩

  4. Sklearnのソースコードを読むと、scipy.linalg.svdで計算した特異値の2乗の累積和で計算しているのですが、explained_variance_で出している値がnp.lilalg.svdで計算した特異値と一致するので、ここでは特異値を2乗せずにそのまま使っています。explained_variance_ratio_もなぜか1乗で計算したほうがあっています。不思議。　https://github.com/scikit-learn/scikit-learn/blob/bac89c2/sklearn/decomposition/pca.py#L444 ↩

232
205
11

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
232
205

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?