始めに##
手書き数字を分析するのもなんだかシリーズ化してきましたが、今回は主成分分析(PCA:Principal Component Analysis)とその教師ありバージョンとも呼べる線形判別分析(LDA:Linear Discriminant Analysis)をつかって分析をしてみたいと思います。pythonの機械学習ライブラリscikit-learnを使っています。
【過去の手書き数字データ分析記事】#####
手書き数字をpythonでもてあそぶ その1
[手書き数字をpythonでもてあそぶ その2(識別する)]
(http://qiita.com/kenmatsu4/items/2d21466078917c200033)
【機械学習】k-nearest neighbor method(k最近傍法)を自力でpythonで書いて、手書き数字の認識をする
主成分分析 (PCA)##
まずは主成分分析からです。基本的には複数あるデータの要素をまとめて、いわゆる主成分を取り出す分析です。機械学習では主に対象データの次元削減を意図して使われることがあると思います。ここで扱っている手書き数字は28x28=784ピクセルの画像データなので、784次元ベクトルになりますが、この次元を削減することを試みます。
主成分分析のイメージ###
下記の図のように2次元の情報を1次元に落とす例で説明します。
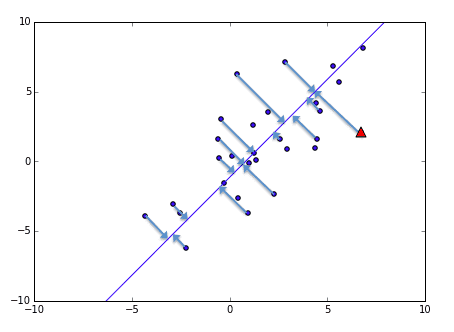
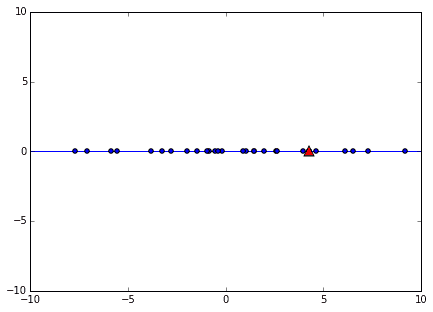
よく使われる例で、国語,算数,理科,社会などの各教科の成績から理系能力、文系能力のように2つの主成分を取り出してみるというのがあると思いますが、これでイメージの説明をしたいと思います。図に表したいので2つの教科、横軸を数学・縦軸を理科の成績とするテストデータを使います。この場合、数学と理科は共に理系の能力なので相関がありそうですよね。青い直線が主成分:理系能力を表しています。矢印で表しているように、各データからこの直線に垂直な線を落とした所が理系の能力として1次元のデータで表現することができます。
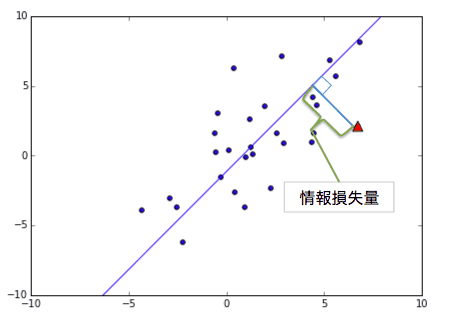
下図で示したデータ点から主成分の直線に落とした垂線の長さを情報損失量と呼びます。次元削減をした時に失われる部分のことですね。主成分の直線はデータの平均点を通り、この情報損失量が最小になる傾きを導出して決めます。ここも最小二乗法ですね。情報損失量の二乗和を最小にする計算をしています。
何次元まで落とす?###
先ほど情報損失量の話に触れましたが、それと表裏一体の関係にある寄与率という概念もあります。大まかに言うとその主成分でどのくらい説明ができているか、の割合の事です。先ほどの数学・理科を理系能力として集約した例で言うと
1 = 第1主成分の寄与率(理系能力) + 情報損失した割合(その他) = 0.89997 + 0.10003
で、約90%が1つの次元で説明できたことになります。
さて、ひとまずpythonで書き数字データに対して主成分分析を行ってみます。まずは、データ全体に対して行うのではなく、各数字ごとに分けて各数字ごとのデータのばらつきを対象がどうなるか、について分析してみます。
以下が主要なコード部分です。(コードの全体はこちら)
# データの読み込み
raw_data= np.loadtxt('train_master.csv',delimiter=',',skiprows=1)
# dataset = DigitDataSet(raw_data)
dataset = DigitDataSet(raw_data)
data = [None for i in range(10)]
for i in range(10):
data[i] = dataset.getByLabel(i,'all')
# 主成分分析の実行
# 削減後の次元数による寄与率の違いを算出
comp_items = [5,10,20,30] # 削減後次元数のリスト
cumsum_explained = np.zeros((10,len(comp_items)))
for i, n_comp in zip(range(len(comp_items)), comp_items):
for num in range(10): # 各数字ごとに分析をかける
pca = decomp.PCA(n_components = n_comp) # 主成分分析オブジェクトの作成
pca.fit(data[num]) # 主成分分析の実行
transformed = pca.transform(data[num]) # データに対して削減後のベクトルを生成
E = pca.explained_variance_ratio_ # 寄与率
cumsum_explained[num, i] = np.cumsum(E)[::-1][0] # 累積寄与率
print "| label |explained n_comp:5|explained n_comp:10|explained n_comp:20|explained n_comp:30|"
print "|:-----:|:-----:|:-----:|:-----:|:-----:|"
for i in range(10):
print "|%d|%.1f%|%.1f%|%.1f%|%.1f%|"%(i, cumsum_explained[i,0]*100, cumsum_explained[i,1]*100, cumsum_explained[i,2]*100, cumsum_explained[i,3]*100)
削減後の次元数が5, 10, 20, 30の場合の各累積寄与率を表にしたのが下記です。例えば次元数30の場合、元の次元数784から30に削減して、その30次元ベクトルで何%が説明されているか、を表します。数字ごとにばらつきがありますが,30次元くらいまで取れば大体7,8割が説明できるようになりますね。784から30と約4%くらいの次元数まで削減してますが7,80%も説明できていると考えるとなかなかです。
| label | explained n_comp:5 | explained n_comp:10 | explained n_comp:20 | explained n_comp:30 |
|---|---|---|---|---|
| 0 | 48.7% | 62.8% | 75.9% | 82.0% |
| 1 | 66.6% | 76.6% | 84.8% | 88.7% |
| 2 | 36.5% | 51.9% | 67.2% | 75.3% |
| 3 | 39.7% | 53.7% | 68.3% | 75.8% |
| 4 | 39.4% | 56.3% | 70.7% | 77.9% |
| 5 | 42.3% | 55.5% | 69.7% | 77.0% |
| 6 | 44.5% | 59.7% | 74.0% | 80.9% |
| 7 | 45.9% | 61.0% | 74.2% | 80.6% |
| 8 | 36.3% | 49.6% | 65.5% | 74.1% |
| 9 | 43.2% | 58.5% | 73.4% | 80.4% |
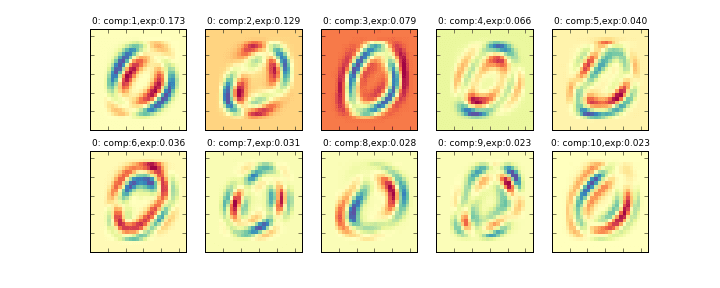
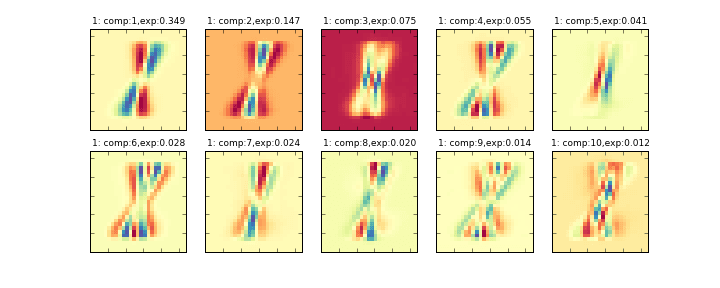
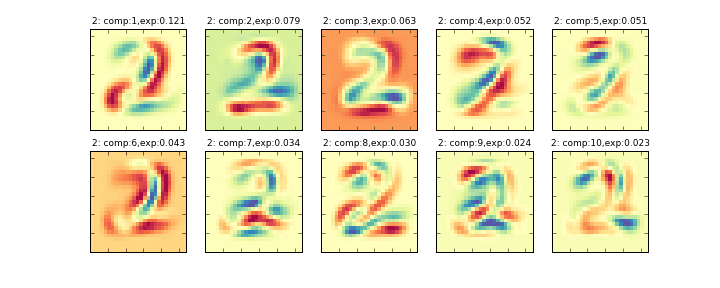
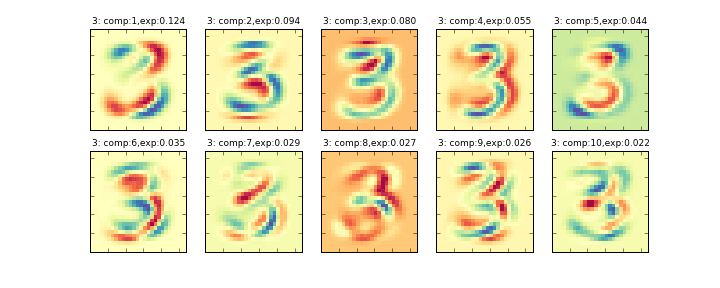
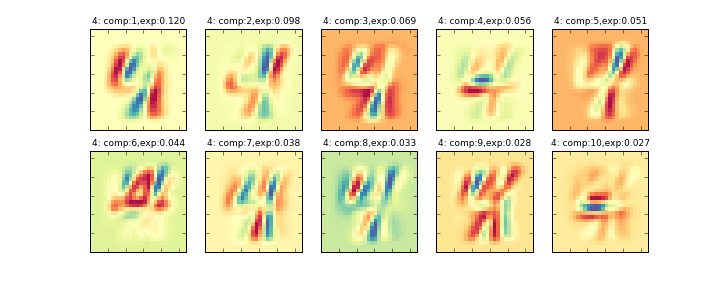
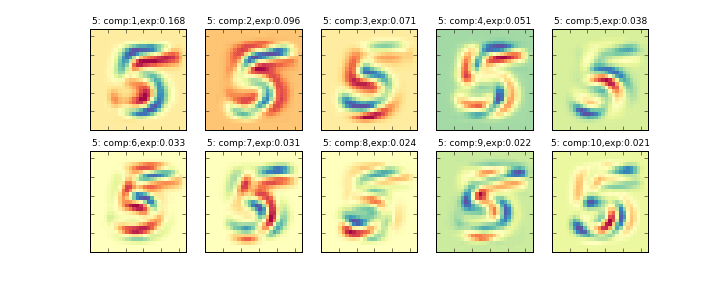
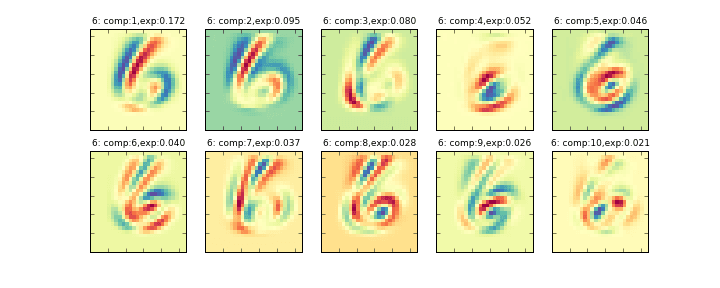
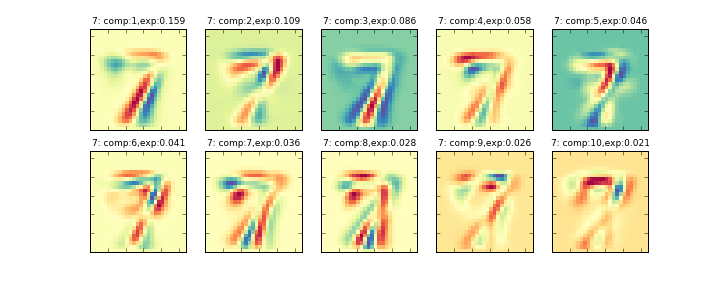
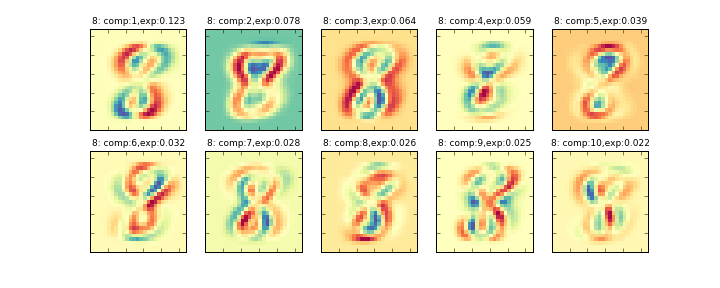
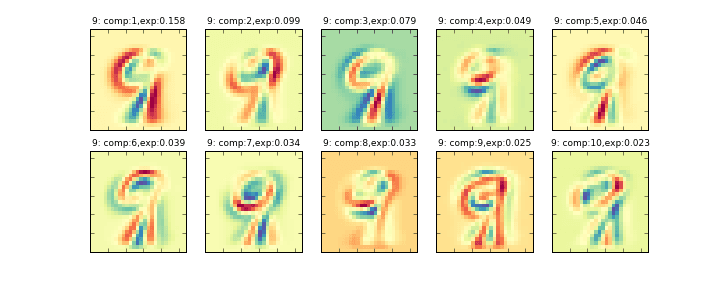
その削減後の10個の主成分を画像化したものが下記のグラフになります。左上から順に寄与率の大きい順に並んでいます。(exp:の部分が寄与率)
データ全体に主成分分析をかける###
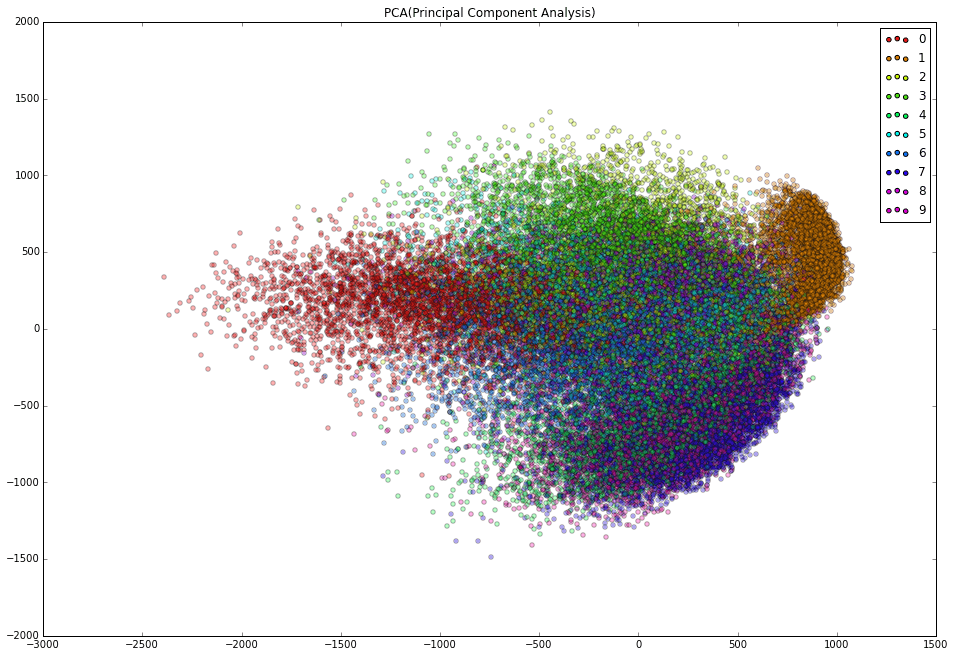
先ほどは、各数字ごとに主成分分析をかけましたが、次に全データ43000個の数字データに対して主成分分析をかけて、エイやっと2次元にまで次元を落とします。784次元から2次元だと落としすぎのようですが、2次元にするとグラフがかけるのです。その全データを2次元にプロットしたのが下記のグラフです。
かなりごちゃっとしている図になってしまいました。主成分分析は各データ点がどの数字か、ということを考慮せずにひとまとめにして主成分を算出するためこうなってしまっています。各点に対してどの数字か、ということを考慮した分析がLDAなのですが、これは次回に説明したいと思います。
いずれにせよ、2次元に落としてグラフで観れるというのは大きなメリットではないかと思います。
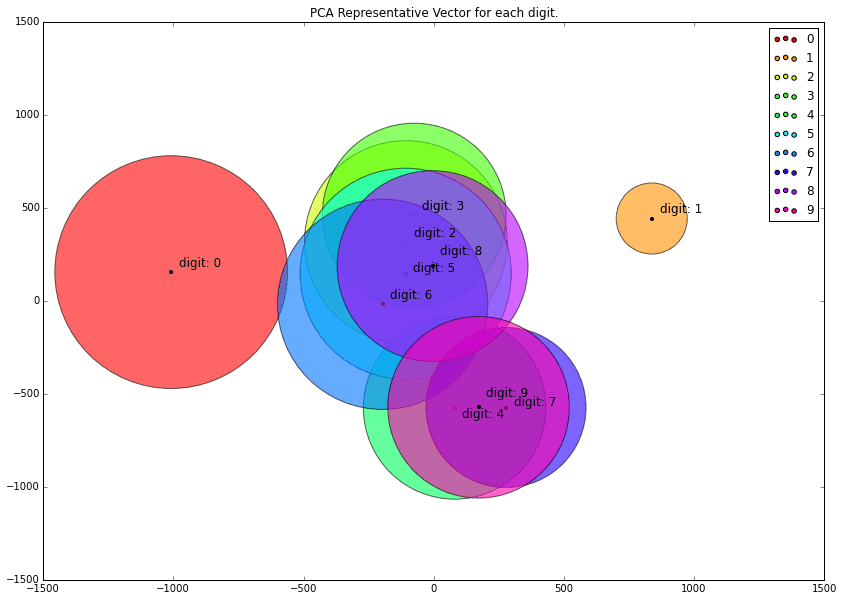
平均した点をプロットして、分散に比例した大きさで表現したグラフ
pythonコードの主要部分はこちらです。
# PCA ALL
pca = decomp.PCA(n_components = 2)
pca.fit(dataset.getData())
transformed = pca.transform(dataset.getData())
colors = [plt.cm.hsv(0.1*i, 1) for i in range(10)]
plt.figure(figsize=(16,11))
for i in range(10):
plt.scatter(0,0, alpha=1, c=colors[i],label=str(i))
plt.legend()
for l, d in zip(dataset.getLabel(), transformed):
plt.scatter(d[0],d[1] , c=colors[int(l)], alpha=0.3)
plt.title("PCA(Principal Component Analysis)")
plt.show()
# 各数字の代表値をグラフで描画
transformed = [pca.transform(dataset.getByLabel(label=i,num=('all'))) for i in range(10)]
ave = [np.average(transformed[i],axis=0) for i in range(10)]
var = [np.var(transformed[i],axis=0) for i in range(10)]
plt.clf()
plt.figure(figsize=(14,10))
for j in range(10):
plt.scatter(100,100, alpha=1, c=colors[j],label=str(j))
plt.legend()
plt.xlim(-1500, 1500)
plt.ylim(-1500, 1500)
for i, a, v in zip(range(10), ave, var):
print i, a[0], a[1]
plt.scatter(a[0], a[1], c=colors[i], alpha=0.6, s=v/4, linewidth=1)
plt.scatter(a[0], a[1], c="k", s=10)
plt.text(a[0], a[1], "digit: %d"%i, fontsize=12)
plt.title("PCA Representative Vector for each digit.")
plt.savefig("PCA_RepVec.png")
plt.show()
つづきます。